高占比新能源电源接入区域电网的无功优化策略研究
2022-07-09韩旭杉王维洲潘卫国陈子文
韩旭杉, 王维洲, 时 帅, 潘卫国, 陈子文
(1.国网甘肃省电力公司, 甘肃 兰州 730070; 2.上海电力大学, 上海 200433)
在当前“碳达峰、碳中和”的大背景下,可再生能源的发展引发了较大关注,也成为解决能源问题的必然途径,各个国家都加大了对新能源的研究力度[1]。数据显示,在 2020 年年底时,全国新能源装机容量占总装机容量的24.3%,风电、光伏新增容量较上年增长幅度较大,分别为178.7%和81.7%,达到7 167万kW和4 820万kW[2]。习近平总书记在气候雄心峰会上强调需要加大新能源的发展力度,进一步提升非化石能源的占比,力求在2030年时将其在一次能源消费中的占比达到 25%上下,其发电量占比需达到50%[3]。
高占比的风电、光伏等新能源接入改变了区域内电网的潮流分布,导致无功潮流发生变化,由此影响了电压质量,不利于电网的稳定运行。结合现有研究可知,新能源出力难以保持较高的稳定性,大大增加了电压越限的可能以及网损。因此,需要结合这些问题进行有针对性的设计,逐步实现无功的优化调度,有助于提升电力系统运行的稳定性。
从本质上来看,配电网无功优化属于一个典型的非线性规划问题,涉及到较多的变量以及约束条件,求解难度较大。当前该领域的研究较多,很多学者提出了不同的解决方法。有研究提出可以采用内点法[4]和灵敏度分析法为主的线性规划法;还有学者提出可以采用牛顿法[5]、二次规划和混合整数规划[6]等非线性规划法;文献[7]以配电网有功网损最小建立了模型,基于Benders分解法求解主、子问题,但单目标模型已不能满足当前无功优化的需求。
近年来,诸多智能化算法开始应用于最优化问题的求解,常用方法包括粒子群优化(Particle Swarm Optimization,PSO)算法[8-9]、模拟退火算法、混沌算法[10]、增强型土狼算法[11]、和声搜索算法[12-13]、寻道优化算法[14]等。有学者提出了混合算法,如组合改进的帝国主义竞争算法和侵入性杂草优化[15],此类算法有效补充了传统算法的不足,并且凸显出其优势。部分学者基于此类方法进行了研究,文献[8]针对公共连接点的无功优化方案求解进行了研究,设计了基于PSO算法与Pareto解相结合的方法,文献[16]则提出了一种基于Pareto熵的多目标粒子群优化(Multi-Objective Particle Swarm Optimization,MOPSO)算法,可以得到较好的求解效果。还有学者考虑了综合因素对电网的影响,如文献[17]为抑制地磁感应电流对电网的不良影响,采用MOPSO算法进行无功优化,实现了在扰动下保持电网无功平衡。
1 无功优化数学模型
1.1 目标函数
本文进行的配电网无功优化是在配电网结构、参数、负荷已知的情况下,对无功补偿器出力和有载调压变压器变比进行合理调节,使配电网达到安全稳定运行的目标。本文以系统网损floss和节点电压偏移量fU均最小为目标函数[18],即
(1)
(2)
式中:i,j——节点标号;
N——节点数量;
gij,θij——节点i和节点j之间的支路导纳、电压相角差;
Ui,Uj——节点i和节点j的电压;
Ui,0,Ui,max,Ui,min——节点i电压的额定值、最大值、最小值。
结合上述内容,可得本优化模型的目标函数F=min(floss,fU)。
1.2 约束条件
无功优化的约束条件可划分为等式和不等式约束两种类型。其中,等式约束条件为潮流约束条件,实际上是配电网中各个节点的无功功率和有功功率的平衡约束[19],具体形式如下
(3)
(4)
式中:Pi,Qi——节点i的有功功率和无功功率;
Gij——电导;
Bij——电纳;
H——与节点i连接的节点集合。
不等式约束条件可以进一步划分为多种类型,包括节点电压约束、节点功率约束、机组出力约束,具体形式如下
Ui,min≤Ui≤Ui,max
(5)
Pi,min≤Pi≤Pi,max
(6)
Qi,min≤Qi≤Qi,max
(7)
PGi,min≤PGi≤PGi,max
(8)
式中:Pi,min,Pi,max——节点i有功功率的最小值和最大值;
Qi,min,Qi,max——节点i无功功率的最小值和最大值;
PGi——节点i接入电源的有功功率;
PGi,min,PGi,max——节点i接入电源的有功功率最小值和最大值。
接入电源并联无功补偿装置约束条件如下:
Qc,min≤Qc,k≤Qc,max
(9)
式中:Qc,min,Qc,max——无功补偿容量的最小值和最大值;
Qc,k——动作k的无功补偿容量。
调压变压器的约束条件为
Tmin≤T≤Tmax
(10)
式中:Tmin,Tmax——调压变压器挡位的下限和上限;
Tk——动作k的调压变压器挡位。
2 无功优化算法
2.1 多目标问题优化的数学描述
多目标优化问题[20](Multi-Objective Problem,MOP)需要采用合适的方式进行描述和求解,从数学角度上可以将最小化多目标优化问题描述为如下形式
(11)
在式(11)中,x1=[x1,x2,x3,…,xn]是n维决策空间X中的向量,x∈X⊂Rn;y=[y1,y2,y3,…,yM]是M维目标函数变量,y∈Y⊂RM;F(x)的M个目标函数对应相同数目的映射函数;gi(x)=0表示不等式约束条件,其数目为p;hi(x)=0表示等式约束条件,其数目为q。
对于多目标优化问题而言,不同的目标函数之间不可避免地存在冲突问题,无法同步达到最小,需要在这些目标函数之间进行一定的权衡,在此基础上才可以得到对应的最优解。此过程中的部分定义如下。
存在两个向量x′,x∈X,当且仅当x′在所有目标函数fi(x1)中具有与fi(x2)相等,或至少一个比fi(x2)更好的值时,那么解x′优于x,记作x′>x,即x′占优x。数学描述如下
∀i∈{1,2,3,…,M},[fi(x′)≤fi(x)]∧
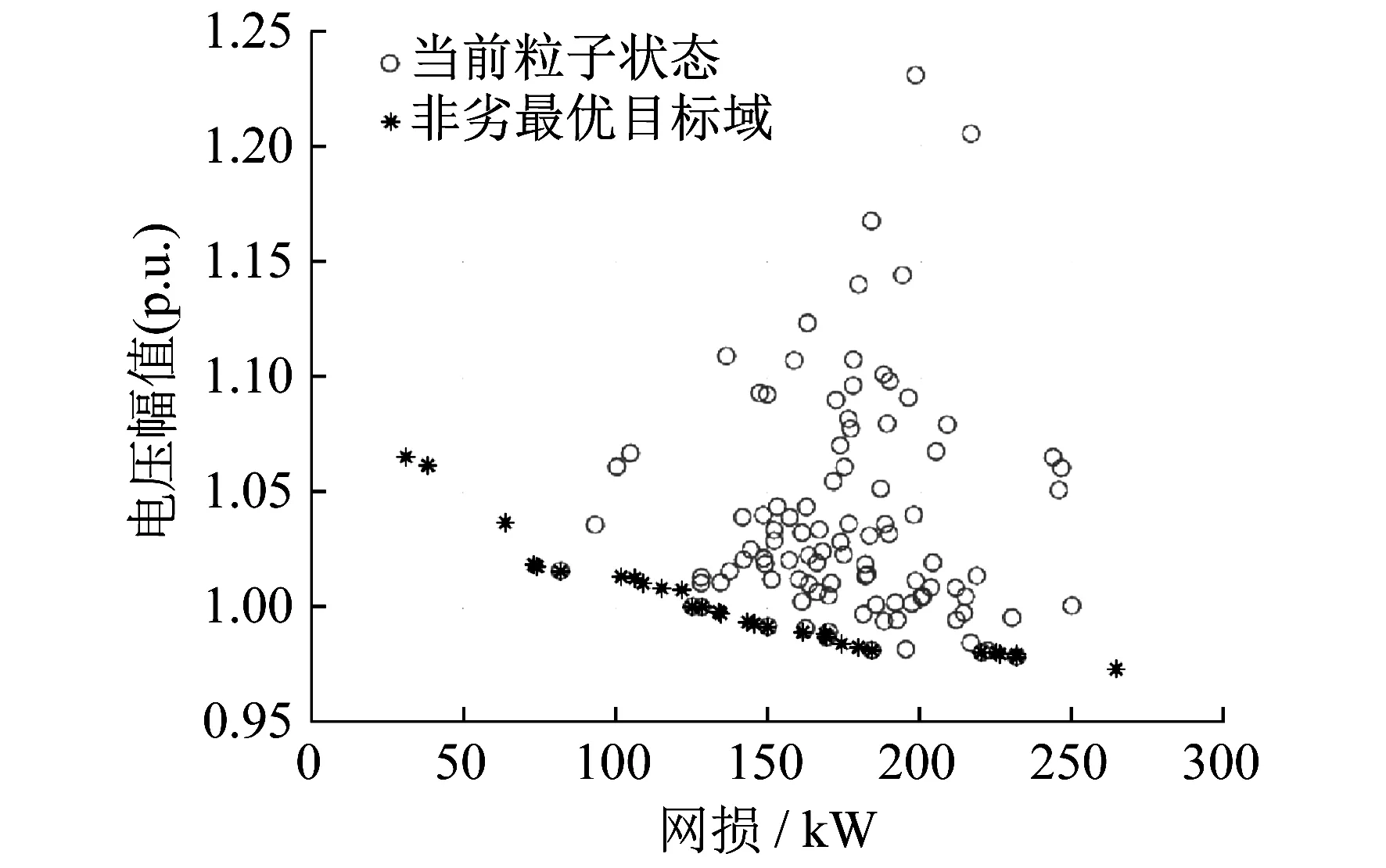
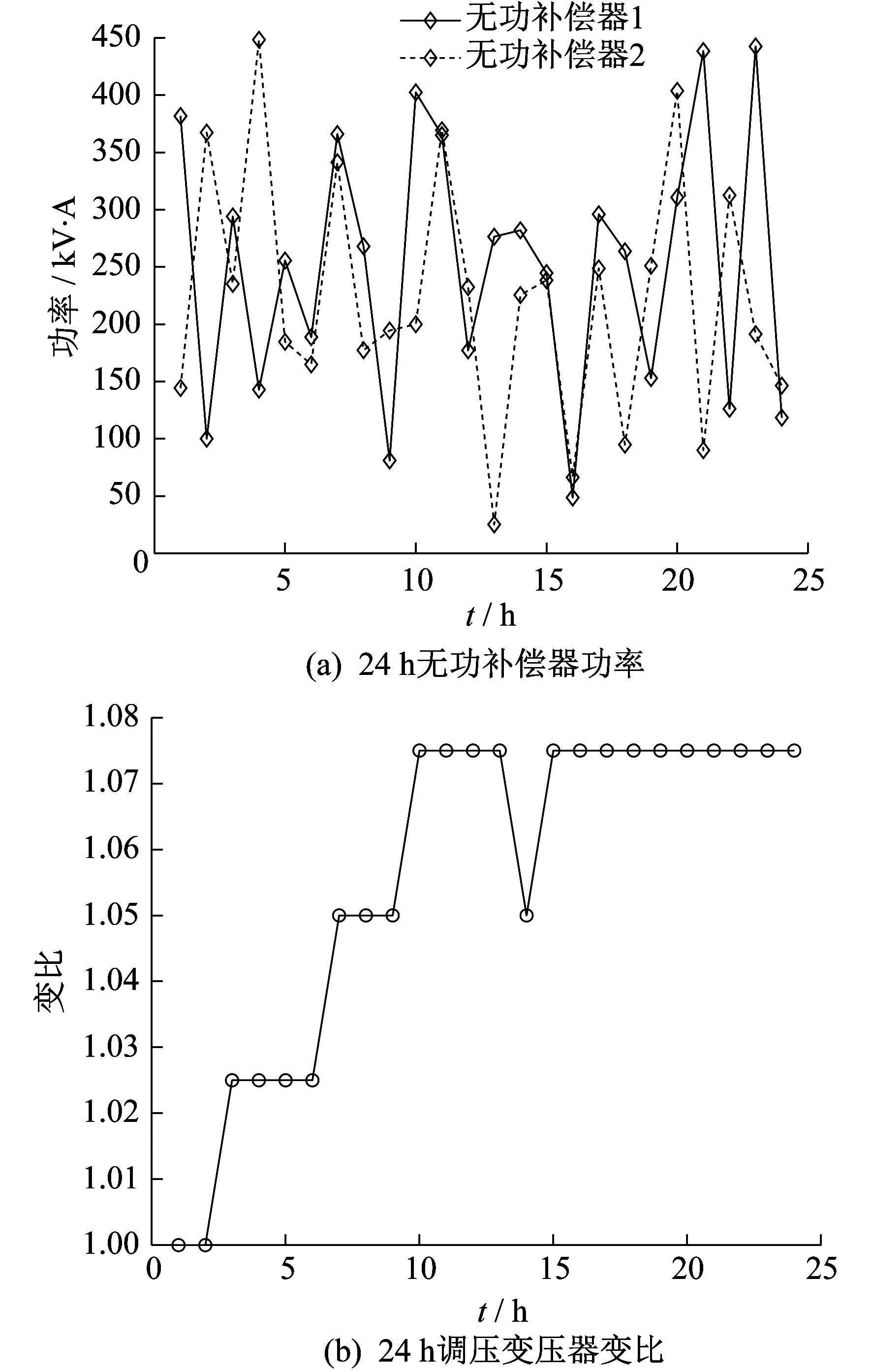
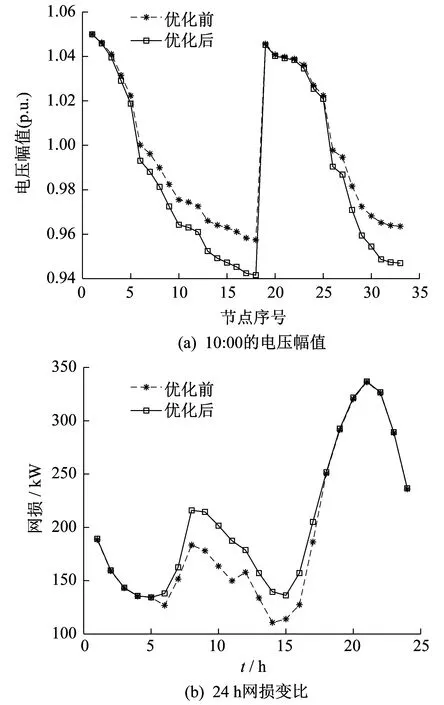
∃i∈{1,2,3,…,ο},[fi(x′) (12) 从式(12)可知,如果一个优化方案在目标函数中具有与另一个优化方案相等或至少一个更好的效果,那么它就比另一个优化方案更好。在这种情况下,一个解优于另一个解。如果这两个解互不占优,则可称为非支配解。 与单目标搜索空间类似,多目标搜索空间中的变量范围决定了每个维度的搜索空间边界,并对其进行约束。等式约束和不等式约束条件的作用与在单目标搜索空间中非常相似。对于每一个多目标问题,在目标之间都有一组最佳的权衡,这就是Pareto最优前沿。 2.2.1 基本粒子群算法 在20世纪末期出现的PSO算法得到了较多的关注[21]。粒子主要利用自身经验以及其他粒子的最优经验对下一步运动进行决策。该算法在迭代过程中主要基于极值来实现自我更新,具体包括个体极值pbest和全局极值gbest。已知粒子群规模为N,粒子i(i=1,2,3,…,N)的位置表示为Xi,速度表示为vi,对应的最优位置是pbest[i],粒子i的速度和位置更新公式为 (13) 式中:w——惯性权重; c1,c2——学习因子; r1,r2——随机数,取值为[0,1]; pbest[g]——粒子g对应的最优位置。 式(13)可以划分为3个部分,依次对应粒子的当前状态、认知以及社会部分。三者作用不同,但是共同影响了粒子的寻优能力,基于三者的配合使得粒子可以达到最优的位置。各个部分的基本功能如下:第1部分实现局部搜索,并平衡全局;第2部分防止陷入局部最小;第3部分则与粒子之间的共享信息有关。 2.2.2 MOPSO算法 本文针对MOPSO算法进行了研究和设计。假设将函数f1(x)和f2(x)极小化,此时的目标搜索空间如图1所示。图1中,目标向量A的变化受到f1(x)和f2(x)的共同约束,使其不在这两个方向上发生改变。在这种情况下A将会沿v1和v2间某一f1(x)和f2(x)不同时增大的方向变化,最终到达非劣最优目标域。B1,B2,C均为A的变化量,且C比B1和B2更接近非劣最优目标域。 图1 目标搜索空间 本文以电压偏移量和网损均最小为目标函数。下面给出2个目标函数优化的算法流程。 步骤1 配电网系统参数设置以及初始化粒子群。根据配电网以及对应的约束条件来确定各个参数,其中初始位置和速度分别表示为Xi和vi,群体规模为N。 步骤2 适应度值采用目标函数f1(x)和f2(x)计算。 步骤3 基于f1(x)和f2(x)分别计算粒子i对应的个体极值pbest[1,i]和pbest[2,i],具体形式为 (14) 步骤4 求解2个目标函数的全局极值gbest[1]和gbest[2]分别为 (15) 步骤5 基于自适应参数选择来计算gbest[1]和gbest[2]的均值gbest和距离dgbest (16) 步骤6 计算pbest[1,i]和pbest[2,i]之间的距离dpbest[i]。 步骤7 计算pbest[i]。 步骤8 用步骤5和步骤7所得的gbest和pbest[i]更新每个粒子的速度vi和位置Xi。 步骤9 若达到结束条件,则输出对应的无功优化方案;若未达到条件,则返回步骤2,具体可以依据决策者的实际要求来选择合适的方案。 针对MOPSO算法的应用效果进行测试分析,其中IEEE-33节点系统的基本结构如图2所示。图2中,C1和C2为无功补偿装置。 图2 IEEE33节点系统的基本结构 对于IEEE-33节点系统而言,存在有载调压变压器,其额定容量为31.5 MV·A,分接抽头达到了110±9×1.25%/10.5 kV的调压容量。另外,还将无功补偿装置设置在15和30这2个节点的位置,其参数设置如表1所示。在节点19接入2台额定值为250 kW的风电机组,节点30接入额定值为250 kW的光伏机组。三相功率、线电压的基准值分别是10 MV·A和12.66 kV。 表1 IEEE33节点系统无功补偿器参数设置 采用MOPSO算法进行无功优化后的Pareto前沿解如图3所示。从图3中提取5种配电网无功优化方案如表2所示。 图3 Pareto前沿解 表2 配电网无功优化方案 根据图3和表2可知,并不存在能够使电压偏移量和网损同步实现最优的方案。其中网损最低的是第2种方案,仅为78.98 kW,但是其对应的电压偏移量最大;第3种方案则恰好相反,虽然电压偏移量最小,但是对应的网损最高,所以应该结合对于电压以及网损的要求来选择合适的方案。除了上述2种方案之外,也可以选择其他3种方案,以实现在网损和电压偏移量上的平衡。 典型日24 h无功补偿器功率变化和调压变压器变比变化如图4所示。选取典型日9:00~15:00为时间段进行分析,此间光伏出力波动和风电出力波动较大,具有代表性。在9:00~10:00,风电出力波动较大,无功补偿器和调压变压器变比变化幅度较大,以靠近风电的无功补偿器1最为显著,涨幅达391.3%;10:00~13:00,新能源出力较为平缓;14:00时光伏出力波动剧烈,无功补偿器2和调压变压器变比变化幅度较大,无功补偿器2降幅达92.3%。由此可见,新能源出力波动使得无功优化策略可以及时改变,以实现平滑风光出力的波动,减少电网潮流波动,进而降低配电网的网损。 图4 典型日24 h内无功补偿器功率和调压变压器变比的变化 采用MOPSO算法进行无功优化前后,典型日10:00电压偏移量和24 h网损变化如图5所示。由图5可以看出,通过MOPSO算法进行无功优化后,电压偏移量均处于安全裕度0.95~1.05范围内,不存在越限的情况,且网损显著降低。选取光伏波动范围较大的9:00~15:00为计算周期,运用本文所提无功优化模型对改进算例进行计算。最终结果表明,网损减少值相对最低的在7:00,优化前网损为158.245 kW,优化后网损为150.523 kW,减少了5.9%;网损减少值相对最高的在10:00,优化前网损为184.006 kW,优化后网损为155.508 kW,减少了18.7%;计算24 h内的总网损,优化前为4 325.274 kW,优化后为3 581.255 kW,减少了17.2%。因此,采用MOPSO算法进行有源配电网的动态无功优化对降低网损具有一定优势。计算结果表明,无功补偿设备的接入在很大程度上缓解了因分布式电源接入造成的配电网电压抬升的问题,可将全网电压调整到0.95~1.05(p.u.)的合理范围内,节点电压平均偏移值为0.04(p.u.),电压稳定性提升了46.3%。 图5 无功优化前后典型日10:00电压幅值和24 h网损变化 本文提出了一种基于Pareto解的MOPSO优化算法,以电压偏移量和网损最小化为双目标函数。根据最终结果可以得出以下结论: (1) 基于自适应系数的MOPSO算法考虑到了算法性能与惯性权重之间的关系,在调整惯性权重时充分利用了算法提供的有用信息,避免了在求解无功优化方案时陷入局部最优解,得出的Pareto前沿解能够为决策者提供不同偏好的决策意见,根据实际情况采用不同的实施方案; (2) MOPSO算法在多目标函数求解中具有一定的优势,用尽可能少的计算资源得到覆盖整个搜索空间、分布均匀、靠近真Pareto前沿解的无功补偿装置的配置方案,可以达到较高的效率和稳定性,所以适用于非线性问题的求解。
2.2 多目标粒子群算法

3 算例分析及仿真
3.1 算例介绍
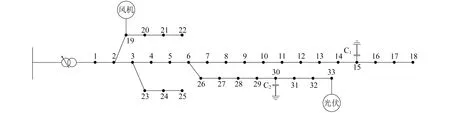

3.2 算例分析

4 结 论
