认证背景下高校师范生教学技能评价体系构建——以衡水学院为例

陈 萍，崔红芳，马南南，李永霞

认证背景下高校师范生教学技能评价体系构建——以衡水学院为例

陈 萍a，崔红芳a，马南南a，李永霞b

（衡水学院 a. 数学与计算机科学学院；b. 教务处，河北 衡水 053000）

以衡水学院数学与应用数学专业师范生为调查对象，根据数学学科的特点，选取影响数学教学技能的12个指标，由指标的特点，将其划分为3大类：教学设计技能、课堂教学技能和教学评价技能，并分别作为由层次分析法构建数学教学技能综合评价体系结构模型的准则层和指标层，根据指标权重的高低得出影响教学技能指标中比较重要的前5项指标，分别为课堂内容变化调控、教学结构安排、课堂内容导入、教学策略选择、教学反思与提高。通过以评价体系中指标层内容为调查内容设计调查问卷，结果表明，该调查问卷具有良好的信度和效度。同时根据调查问卷的数据分析得到影响教学技能的前5项指标与层次分析法得到的指标一致，由此验证了通过层次分析法构建的评价体系的合理性。

师范生；教学技能；评价体系；专业认证；层次分析法；SPSS软件

在我国教师教育不断发展的历程中，国家对师范教育人才培养质量方面的重视程度逐步加大，为了切实提升师范人才质量和促进高等教育的改革，教育部在2017年正式发布了《普通高等学校师范类专业认证实施办法（暂行）》，对师范专业院校进行认证分级[1]。该专业认证实施办法秉承的专业认证理念是“学生中心、产出导向、持续改进”，而专业教学技能在师范生的成长过程中起着非常重要的作用。因此，需要建立一个发展的、多元的评价体系，全面地评价学生在学习过程中的态度和效果等问题。

1 数学专业师范生教学技能培养存在的问题

要想成为一名合格的教师，刚刚毕业的师范生一般是需要经历初任教师、合格教师、优秀教师三个阶段，教学技能是师范生成为一名教师的基本职业能力，师范生想要成为一名合格的人民教师，在学校期间基本的教学技能的训练是必不可少的，可见一名优秀教师的培养不是一蹴而成的，而是要通过层层的锻炼，加强自身的教学技能，才能逐步地靠近优秀教师的行列。师范生的校内专业教学技能的培养主要是通过师范院校开设的专业教学技能课程进行的。通过对衡水学院数学与应用数学专业的师范生进行调研，发现师范生在培养过程中存在着以下问题。

1.1 实践课程在课程体系中所占比例小

实践性课程在培养教师专业技能的方面占有重要地位，不容忽视[2]。以衡水学院数学与应用数学专业的师范生为例，根据数学专业培养方案的设定，师范生在校学习的课程可分为以下4个平台：通识教育课程平台、专业教育平台、对接行业企业课程组平台、素质拓展平台。在通识教育课程平台中主要包括思想政治系列课程，在专业教育平台中主要包括数学专业学生所学习的数学类必修理论课程，在对接行业企业课程组平台中包括初中、高中教师教育课程系列。在整个学习阶段的课程中，教育类的课程主要包括教师职业道德教育法规、青少年心理与发展、教育学原理、青少年认知与学习、教师工作实务指导、汉字书写、教师语言、现代教育技术应用、中学学科课程标准与教材研究、中学学科教学设计、中学学科教学技能训练、中学数学教师资格考试训练教程、数学教育测量与评价等。在这些课程中，很多课程都是偏重纯理论性的，只有中学学科教学技能训练、汉字书写、教师语言是偏重实践性的；有些课程可能会包含有实践环节，但是教师经常会侧重理论讲解，忽视实践内容，由此可知，本专业师范生整个课程体系中专业课程设置较多，而实践性课程明显过少。

1.2 锻炼机会少，实习制度有待完善

目前衡水学院师范生的实习主要包括教育研习、专业实习、专业认知（见习）等，在专业实习方式上主要是通过学校教务处将学生分派到衡水市市区以及县级各中小学，学生到了实习学校后，许多实习学校担心实习生的教学方法影响学校的教学质量，因此不允许学生上讲台上课，只是单纯地随堂听课、帮指导教师批改作业、盯守自习和管纪律。因此学生在整个实习阶段缺少教学实战经验，不能将学习到的理论知识应用到课堂中。

2 数学专业师范生教学技能体系的构建

2.1 教学技能体系指标的选取

不同的学科具有不同的特点，各学科对师范生的教学技能的要求也存在着差异。对于数学专业的学生来说，根据数学学科的特点和衡水学院数学与应用数学专业培养方案中师范学生的培养目标，要求师范生具有能综合运用数学学科知识、教育学原理及现代教育技术优化教学设计、组织课堂教学并讲授中学数学示范课程，能及时进行课后反思及有效评课等具有数学学科特点的能力。

综合考虑学科和指标的特点，参考目前关于影响教学技能具有代表性的文献[3-4]，将评价体系的指标确定为以下12个指标，分别为：教材内容分析、教学策略选择、教学结构安排、教学媒体选择与使用、教案编写、课堂内容导入、课堂内容变化调控、教学语言与提问、板书板画、课堂内容抽象概括、课后辅导、教学反思与提高。

2.2 评价体系的构成

层次分析法[5]是将定性问题进行定量分析的一种多准则决策方法，通过设立一个目标，找出影响目标的因素，用专家打分的方法来判断各因素之间的重要性，并且运用具有逻辑性的过程得到各因素对应目标的权重，最后参考权重得到各因素的优劣。根据前面选取的12个评价指标，由指标的特点，将其划分为3大类：前5个指标作为第一类，即教学设计技能；从第6个指标到第10个指标作为第二类，即课堂教学技能；最后2个指标作为第三类，即教学评价技能。根据层次分析法首先构造教学技能评价体系的结构模型，具体的目标层、准则层和指标层如表1。

表1 教学技能评价体系的结构模型

2.3 构造判断矩阵

根据各个评价指标的重要性，按1—9比例标度对评价指标两两比较构建层次分析法判断矩阵[5]，进一步利用层次分析法矩阵获得各指标的权重，构造目标层和准则层的判断矩阵1，准则层和指标层的判断矩阵分别为11，12，13，

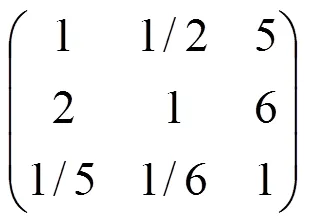
对判断矩阵进行列向量归一化后可求得特征向量，最大特征值，一致性指标=(λ－/(－1)，随机一致性指标（查表可得到），随机一致性比率为=/，当各层次的判断矩阵随机一致性比率均小于0.1时，说明判断矩阵具有满意的一致性，否则就需要调整判断矩阵，使之具有满意的一致性，具体数值如下：

对于判断矩阵1，最大特征值为=3.03，一致性指标=0.01，随机一致性指标=0.52，一致性比率=0.01＜0.1，通过一致性检验，权重为=(0.34，0.58，0.08)。

对于11，最大特征值为=5.35，=0.09，=1.12，=0.08＜0.1，通过一致性检验，权重为11=(0.08，0.24，0.51，0.04，0.14)。

对于12，最大特征值为=5.07，=0.02，=1.12，=0.02＜0.1，通过一致性检验，权重为12=(0.26，0.47，0.05，0.10，0.11)。

相对于13，最大特征值为=2，权重为13=(0.2，0.8)，因为当=2时，=0，2阶的正反矩阵总是一致性，所以满足一致性检验。

根据公式=·得出准则层对目标层的权重，具体权重值及指标排序如表2。

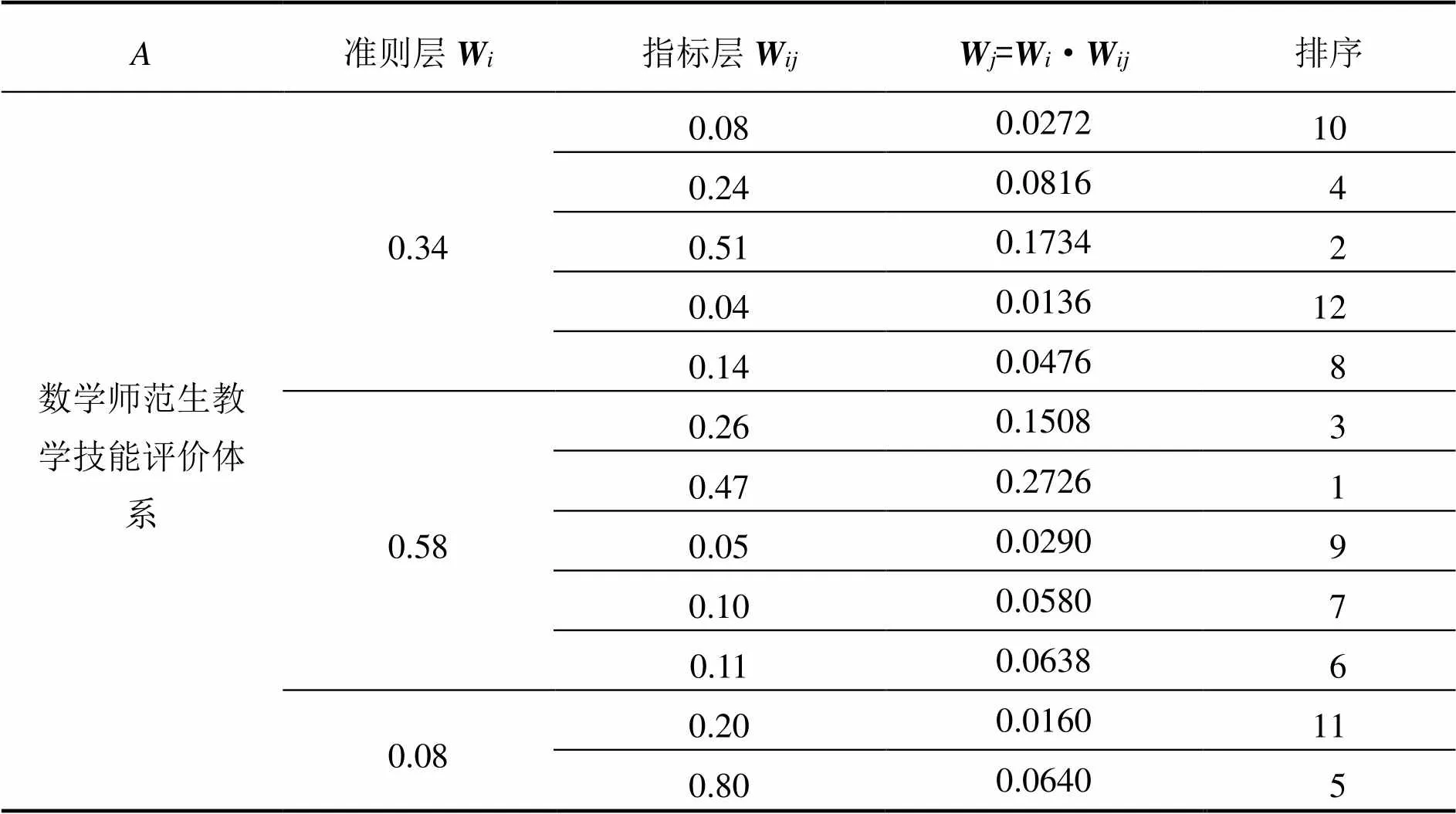
表2 权重值及指标排序

由上表可以看出，在影响教学技能的12项指标中依据权重的高低，排在前5项的依次为：课堂内容变化调控、教学结构安排、课堂内容导入、教学策略选择、教学反思与提高。

3 调查问卷

以上述研究中构建的数学专业师范生教学技能评价体系为基础，设计了一份以评价体系中指标层内容为调查内容的调查问卷。以衡水学院数学与应用数学专业临近毕业的师范生为调查对象。通过问卷星在线问卷调查，最后统计出共86份调查问卷可供使用。根据教学技能评价体系的指标，在问卷设计中12个指标的赋分均采用正向赋分，即设计12个指标在影响教学技能中所占的地位分为5个等级，分别为：很重要、重要、一般重要、不重要、很不重要，其中选很重要计5分，重要计4分，一般重要计3分，不重要计2分，很不重要计1分，通过SPSS软件[6]对得到的调查问卷结果进行内部一致性的信度系数分析，得到克隆巴赫Alph系数＞0.7，根据内部一致性系数检验量表可得到通过层次分析法构建的数学专业师范生教学技能评价体系具有较高的信度，适合于进一步分析。将设计的数学专业师范生教学技能评价体系发送给数学与应用数学专业有关教学论研究方向的专家，征求其意见建议，专家对此评价体系的反馈意见较好，说明此评价体系具有优良的效度。通过上述对建立的评价体系信度和效度的检验结果，可以得出上面设计的该评价体系具有可信性与可靠性。具体的调查问卷的数据如表3。

表3 调查问卷结果

调查问卷的平均分数值的大小表明，影响数学专业的师范生教学技能的12个指标中比较重要的前5项指标为教学结构安排、教学策略选择、教学反思与提高、课堂内容导入、课堂内容变化调控。

由此可知，由层次分析法构建的数学专业师范生课堂教学技能综合评价体系中影响教学技能的前5项指标和调查问卷中得到的影响教学技能的前5项指标一致，这体现了数学专业师范生对教学结构、教学策略、教学反思和课堂内容的重视，符合数学专业对师范生的专业性要求；在重视教学反思与提高这一方面，也符合目前在教师专业发展中对教师“反思”的迫切需求。通过层次分析法得到的评价体系，为提高普通数学专业学生的数学教学能力，为地方高等师范院校培养符合师范类专业认证需要的专业数学教师提供了可行的有效方案。

[1] 中华人民共和国教育部.普通高等学校师范类专业认证实施办法(暂行)[EB/OL].(2017-11-08)[2019-06-10].http://www.moe.gov.cn/srcsite/A10/s7011/201711/t20171106_318535.html.

[2] 郑红梅,马引弟.专业认证背景下数学师范生专业技能的培养[J].西部素质教育,2019,5(16):190-191.

[3] 卢丽静.高校师范生教学技能评价体系研究[D].武汉:华中师范大学,2011.

[4] 王春晓,吴长海.物理师范生教学技能综合评价体系的构建[J].洛阳师范学院学报,2015,34(11):55-57,68.

[5] 谭丽婷,张辉.基于层次分析法的民办高校思政课教学健康度模型设计[J].广东水利电力职业技术学院学报, 2021,19(3):56-59.

[6] 胡典顺,朱展霖.基于SPSS与AMOS的问卷信度效度检验——以数学焦虑、数学态度和数学效能的关系研究为例[J].教育测量与评价,2020(11):3-7,28.

Construction of Teaching Skill Evaluation System for Normal College Students under the Background of Certification——Taking Hengshui University as an Example

CHEN Pinga, CUI Hongfanga, MA Nannana, LI Yongxiab

(a. College of Mathematics and Computer Science; b. Educational Affairs Office, Hengshui University, Hengshui, Hebei 053000, China)

Taking the normal college students majoring in mathematics and applied mathematics of Hengshui University as the survey object, according to the characteristics of mathematics, 12 indexes affecting mathematics teaching skills are selected. According to the characteristics of the indexes, they are divided into three categories: teaching design skills, classroom teaching skills and teaching evaluation skills, which are respectively used as the criterion layer and index layer of the comprehensive evaluation system structure model of mathematics teaching skills constructed by analytic hierarchy process. According to the weight of the indicators, the first five indicators that affect the teaching skills are obtained, which are: the change and regulation of classroom content, the arrangement of teaching structure, the introduction of classroom content, the selection of teaching strategies, teaching reflection and improvement. The results of the questionnaire based on the content of the index layer in the evaluation system show that the teaching skill evaluation system has good reliability and validity. At the same time, according to the data analysis of the questionnaire, the first five indicators affecting teaching skills are consistent with those obtained by analytic hierarchy process, which verifies the rationality of the evaluation system constructed by analytic hierarchy process.

normal college students; teaching skills; evaluation system; professional certification; analytic hierarchy process; SPSS software

10.3969/j.issn.1673-2065.2022.04.017

陈 萍（1968－），女，河北衡水人，教授；

崔红芳（1984－），女，河北衡水人，讲师。

衡水学院校级课题（2021SK15）；衡水学院教育教学改革研究与实践项目（jg2020068）；河北省高等教育教学改革研究项目（2021GJJG536）；衡水学院校级课题（2022SK32）

G420

A

1673-2065(2022)04-0090-05

2022-02-26

（责任编校：李建明 英文校对：李玉玲）