基于Shannon熵的高压直流输电线路单端电气量保护
2022-07-09韩昆仑宋世勇
韩昆仑, 宋世勇
(广西大学电气工程学院, 南宁 530004)
鉴于高压直流输电(high voltage direct current transmission,HVDC)系统具有非同步联网方便、功率调节控制便利、线路造价低、电能损耗小、非常适合于远距离大容量输送电能等诸多优点[1],HVDC的发展在中国受到了极大的重视,工程建设数量、输送容量和输电距离等方面指标迅速增长,如今中国已位居世界直流输电大国之列[2]。然而中国开展HVDC的研究起步较晚,在相关技术方面仍显落后,有关部门已经提出了相应举措逐步提高中国直流输电设备制造、工程建设及运行维护等方面的自主化水平。输电线路故障率高,保护动作正确率普遍较低[3],对其保护的方法主要有单端量保护和双端量保护[4]:单端量保护快速性好但耐高阻故障能力不足,双端量保护的可靠性依赖于通信,经济性差,且存在通信延时,保护动作时间较长[5-7]。针对传统的线路保护方法存在的缺陷,研究人员提出了许多改进和创新方案,对直流输电线路继电保护技术进行了一系列有益的探索[8-15]。例如,文献[8]首先根据整流侧保护安装处故障电流的极性判别故障位于该保护侧区外还是对侧,如位于对侧,则利用逆变侧单端量求取模型误差函数识别故障等效模型,从而区分故障位于线路内部还是逆变侧区外。文献[9]利用各种故障情况下在特定时窗内反行波波形相似性的不同,采用Hausdorff距离算法来衡量其相似度以识别故障类型,耐过渡电阻能力强,但保护依赖于通信传输且算法较为烦琐。文献[10]采用Hilbert-Huang变换算法提取行波波头实现了故障测距功能,构造故障电压高低频能量比值判据识别故障区段,对比采用小波测距的方法其误差更小,但该方法对采样率要求较高。文献[11]基于直流滤波元件对行波波头的平滑特性,区内和区外故障时高频带Hilbert能量幅值及其波形呈现出的显著差异性,与相应的门槛值进行比较识别出故障的区段,可有效地保护线路全长。文献[12]以直流滤波器阻抗-频率特性为出发点,根据区内外故障时两端的线路侧和平波电抗器阀侧在高频带内暂态能量幅值的不同,提出了一种不受分布电容影响的纵联保护方法,快速性好。文献[13]考虑了长线路的衰减特性,以单端保护装置检测到暂态电流的高、低频段小波能量作为保护判据电气量,以其相互之间的比值构造保护判据实现故障判别,同时能够对线路雷击故障和雷击干扰进行区分识别,保护判据较多。文献[14]研究发现反行波电压幅值积分在不同类型故障时具有明显的大小之分,利用此项特征形成了快速性能良好的纵联保护方法,对通信速率和数据同步要求低,可作为直流线路快速后备保护。
目前对于直流线路保护技术的研究,比较多的学者采用小波分析、HHT(Hilbert-Huang transform)等手段在频域内对故障信号进行特征提取及分析进而构造保护算法,成了研究的热点。而这些算法存在着小波基没有统一的选取原则、分解易出现模态混叠现象而可能导致分析结果不准确等问题,同时其计算过程烦琐,时效性不高。针对此问题,现提出一种基于熵值分析的保护方案,其原理简单,可有效避免传统保护算法因计算量大且耗时长的弊端。研究线路边界直流滤波元件的阻抗-频率特性及暂态电流特征频带分量的分布特点,利用切比雪夫数字滤波器提取频带电流,通过求取其Shannon熵值来提取相应特征以实现故障类型的区分,并利用暂态电流变化特征构造相应判据实现保护启动和选极功能,形成一种仅使用单端电气量的保护方案。在PSCAD/EMTDC及MATLAB平台进行仿真、验证,证明所提方案具有可行性。
1 直流线路边界特性及故障特性分析
1.1 HVDC线路边界
HVDC系统结构主要包括交流系统、换流变压器、换流器、直流滤波元件和输电线路[13]。直流滤波元件由平波电抗器和直流滤波器构成,也称为线路边界[15],配置于线路首末端而形成了线路两端的阻抗不连续点。目前直流工程配备的直流滤波器多为双调谐或三调谐滤波器,用以滤除脉动换流器在直流侧产生的特征谐波,平波电抗器用于平滑直流纹波、限制电流变化率及降低换相失败概率[16]。以某直流工程中的实际配置为例,如图1所示平波电抗器和12/24/36三调谐滤波器组成了线路边界。

图1 直流输电线路边界Fig.1 DC transmission line boundary
图1中,M为直流滤波器出口线路首端保护安装处,平波电抗器电抗值为L,直流滤波器组电容、电感值分别为C1、C2、C3、C4、L1、L2、L3、L4。设平波电抗器阻抗为Z1,两个直流滤波器阻抗为Z2、Z3,其并联阻抗为Z4,则
Z1= jωL
(1)
(2)
(3)
Z4=Z2‖Z3
(4)
式中:ω=2πf;‖表示并联。
1.2 直流线路边界滤波特性及故障特性
图2为上述三调谐直流滤波器组的阻抗-频率特性图,根据图示可知,在特征频率600、1 200、1 800 Hz处,直流滤波器组阻抗取得极小值,阻抗幅值接近于0。显然,在直流系统正常运行及直流线路区外故障时,特征频率谐波难以传输到直流线路上。换言之,滤波器组对位于特征频率附近的电量具有良好的滤波效果。
HVDC系统故障时会在故障点处产生各种频率的暂态信号,而信号能量主要集中在低频带[17],高频带分量能量比低频带小几个数量级。根据前文分析,区外故障时,特征频率附近的暂态分量难以由区外传输到直流线路上,而区内故障时,暂态分量不经过边界滤波环节的滤除作用,使得区内外故障时直流线路上的暂态信号特征频带分量的幅值和波动程度呈现出明显的不同。因此,利用该特征构造的保护判据能够有效判别线路区内外故障。图3~图5分别给出了区内线路末端、区外整流侧及逆变侧平波电抗器阀侧金属性接地故障情况下直流线路首端检测点测量到的暂态电流波形图及暂态电流550~650 Hz特征频带分量波形图,由图3~图5可知,区内故障时频带电流含量远比区外故障时大得多,验证了上述理论分析的正确性。

图2 滤波器阻抗-频率特性Fig.2 Impedance frequency characteristics of filter
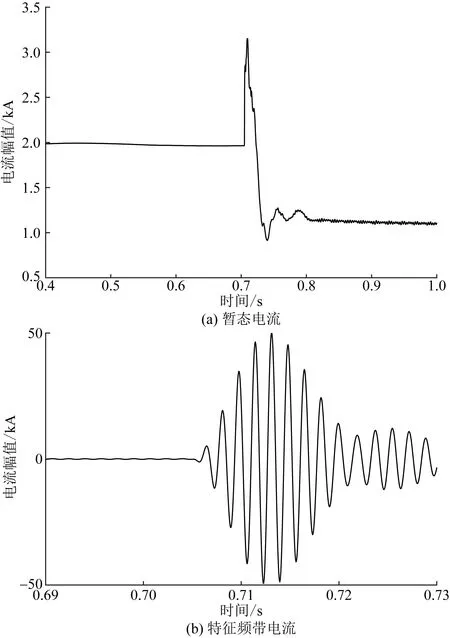
图3 线路末端故障Fig.3 Fault at the end of line
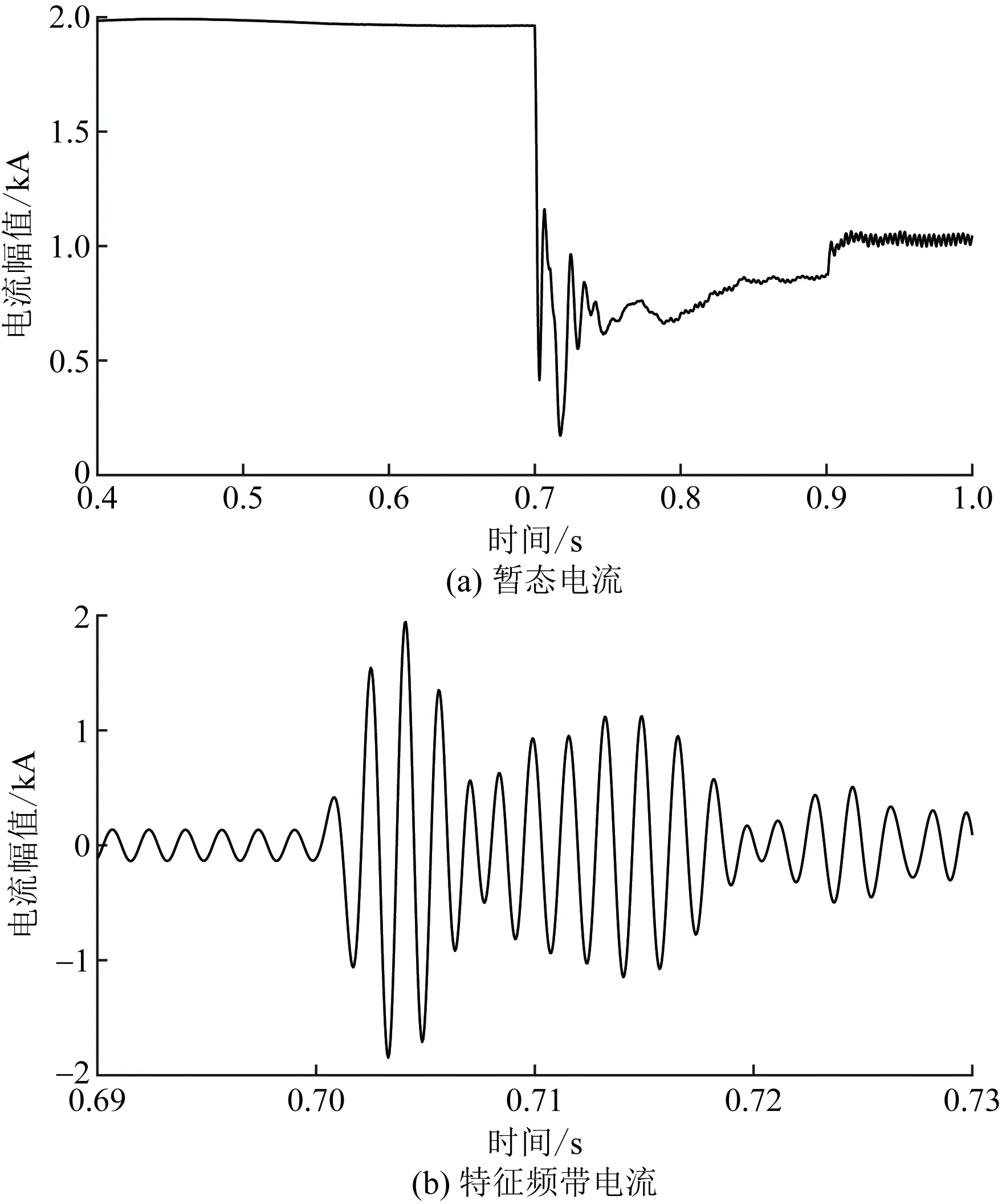
图4 整流侧区外故障Fig.4 External fault at rectifier side

图5 逆变侧区外故障Fig.5 External fault at inverter side
2 Shannon熵原理
信息论创始人Claude Shannon将熵的概念引入到信息论中,同热力学和分子学中的熵类似,信息论中的熵是表征系统参量分布规则性测度的量。熵值越大,说明信源集合中的参量分布越均匀,不规则性越小;越小则说明信源集合中的参量分布越不均匀,不规则性越大[18]。熵值法作为一种比较现代的特征提取方法已广泛应用于多个领域并取得一定的成果[19],而在电力系统信号分析领域,虽已逐渐受到学者们的关注,但相关方面的研究仍较少,有待进行进一步的探索实践。因此,本文中采用熵值法对HVDC故障进行分析,具有一定的开拓性的研究价值和意义。
熵本身是一个状态函数,电力系统运行的状态可以考虑利用熵值进行评判。熵值分析对于两种不同类型的信号,具有放大其差异特征的能力,其算法简便、高效、区分度高。鉴于此,将利用Shannon熵的统计特性对故障信号进行特征提取,其定义式为(约定lg0=0)
(5)
式(5)中:S为待处理的原始信号;Si为信号S中的采样值。
由1.2节分析得知:由于直流线路两侧边界滤波环节的存在,区内外故障时,单端保护装置测量到的暂态电流特征频带分量的分布具有明显差异。由于故障信号低频带能量较高频带大得多,为避免因故障信号高频分量能量过小而导致定值选取困难的问题,同时为保证有足够的区分度,选取暂态电流550~650 Hz频带分量作为分析对象较为合理。本文中采用Chebyshev带通滤波器提取上述频带的暂态电流分量。区内故障时的暂态电流特征频带分量比区外故障时的暂态电流特征频带分量含量高、波动幅度更大,信号中的参量分布更不均匀,两种情形下的熵值显然不同。
3 保护方案
3.1 故障区段识别主判据
直流系统故障后,可利用不同故障情况下保护处检测到的暂态电流信号550~650 Hz频带分量的Shannon熵值的不同构造保护识别判据,实现故障区段的定位,保护判据式为
P=H(I550~650 Hz)≤Pset
(6)
式(6)中:I550~650 Hz表示暂态电流550~650 Hz频带分量的采样信号;H为频带电流的Shannon熵;P为识别因子;Pset为保护识别为线路保护区内故障的门槛值。满足该式则识别为区内故障,否则为区外故障。其门槛值Pset按躲过直流线路区外故障情况下取得的特征频带分量电流Shannon熵值的最小值进行整定。根据大量仿真试验并进行相关灵敏度校验,文中Pset值取为0时,能可靠识别故障区段,工程中可根据实际需要进行调整。
3.2 启动判据和选极判据
观察图3(a)、图4(a)、图5(a)可知,直流系统正常运行时电流无突变,故障发生后,暂态电流发生突变并达到一定的阈值,故可构造启动判据为
(7)
式(7)中:Q定义为保护启动因子;ΔI(i)为第i个采样点的电流突变量值;N为采样点数;Iset为电流保护启动的门槛值,其门槛值Iset应小于故障条件下电流突变量取得的最小值。结合文中所采用的仿真系统模型参数,根据大量的仿真验证,文中Iset取0.3 kA时可确保故障发生时保护启动元件可靠启动。
由于双极耦合效应,单极线故障时,非故障极亦将感应到特征频带的暂态电流,但其幅值将显著小于故障极。如图6给出了正极直流线路中点处金属性接地故障时正负两极线路测量到的特征频带电流波形图,显然看出,负极线上感应出的特征频带电流远小于正极线。因此可构造选极函数为
(8)
K=S1/S2
(9)
选极判据为

图6 正极线中点故障时双极线上的特征频带电流Fig.6 Characteristic frequency band current on bipolar line in case of neutral point fault of positive pole line
(10)
式中:m取1、2表示正负极;Sm表示m极暂态电流频带分量幅值积分;K为选极因子,定义为正、负极线上暂态电流频带分量幅值积分的比值;Kset1和Kset2为选极门槛值。发生极间短路故障时,K接近于1;发生单极故障时,由于极线耦合的影响,在一极线路末端高阻故障时,两极保护安装处测得的特征频带电流相差较小,因此,为保留一定的裕度,选取Kset1=1.2、Kset2=0.8。
3.3 采样频率的选取
为合理选取数据的采样率,文章以最不易于进行区分的两种故障类型举例:线路末端故障及逆变侧平波电抗器阀侧区外故障,采样频率分别取50、20、10 kHz,考察采样频率对保护性能的影响,试验结果如表1所示。

表1 故障时不同采样频率下的Shannon熵值Table 1 Shannon entropy at different sampling frequencies during fault
由表1可知,随着数据采样频率的提高,区内外故障时保护识别因子的差异更为明显,即采样频率越高越有利于故障类型的准确区分。但所述三种情况下,区内故障时识别因子始终小于保护动作门槛值0,区外故障时始终大于保护动作门槛值0,因此10 kHz的数据采样频率仍然能满足保护所需数据量的需求。同时,考虑到过低的采样率将不能完整地反映出原始信号包含的信息,且目前实际运行中的直流控制保护系统采样率为10 kHz,本文中选取10 kHz的数据采样率,对采样要求并不高,亦能满足实际工况。
3.4 保护方案流程
文中所提方案保护装置由启动元件、故障识别元件和选极元件构成。在满足保护启动式[式(7)]后,保护装置启动并进入故障识别程序,在判别为区内故障后进行故障的选极,相应保护装置做出正确响应,文章所提保护方案流程图如图7所示。
4 仿真验证
在CIGRE HVDC模型的基础上,参照某实际工程搭建了如图8所示的±660 kV双极HVDC系统的PSCAD仿真模型,系统额定直流电流为2 kA,输电线路长1 400 km。仿真中选取的数据采样频率为10 kHz,时窗长度5 ms,故障发生时刻设置于0.7 s,故障持续时间0.2 s,对多种区内外不同类型故障进行仿真,验证了保护动作的正确性。表2、表3分别为线路区内及区外多种不同类型故障情况下的仿真实验结果。
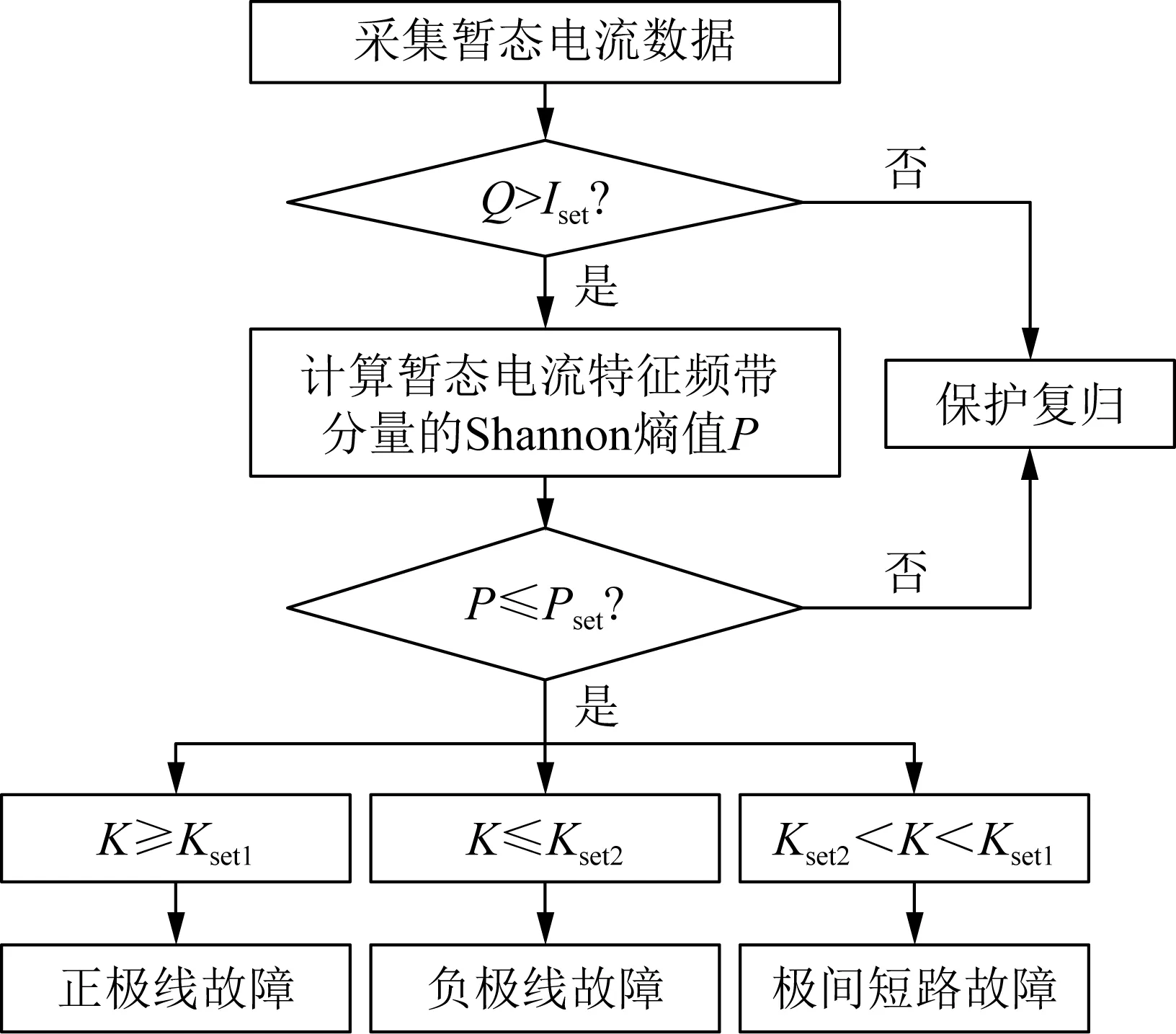
图7 保护方案流程图Fig.7 Flow chart of protection scheme

M、N、P、Q为线路保护安装位置,f1~f9为设置的故障位置图8 双极高压直流输电系统Fig.8 Bipolar HVDC transmission system
依据表2、表3中的仿真结果数据,可见对于区内f1、f2、f3不同位置及不同过渡电阻情况下的故障,其识别因子P始终小于或等于门槛值0;对于区外f4~f9故障,其识别因子P始终大于门槛值0,识别判据能较可靠的定位出故障区段。同时,对于单极故障,正极故障时选极比K恒大于1.2,负极故障时恒小于0.8;对于双极故障,选极比K始终在1附近,选极判据在线路故障时可准确地选出故障极线。
5 结论
对直流输电线路继电保护技术的现状进行了简要概述,分析了现有技术包括单端量保护和双端量保护的优势及不足。直流输电对于输电线路的保护要求在毫秒级时间内迅速做出响应,本文则针对快速性能优良的单端量保护进一步展开研究。从研究线路边界滤波元件特性出发,深入挖掘了暂态电流的传播特点,提出了一种基于Shannon熵值的单端电气量保护方法,对实际直流工程中配备的主保护即行波保护的补充和完善具有一定的参考价值,研究得出如下结论。
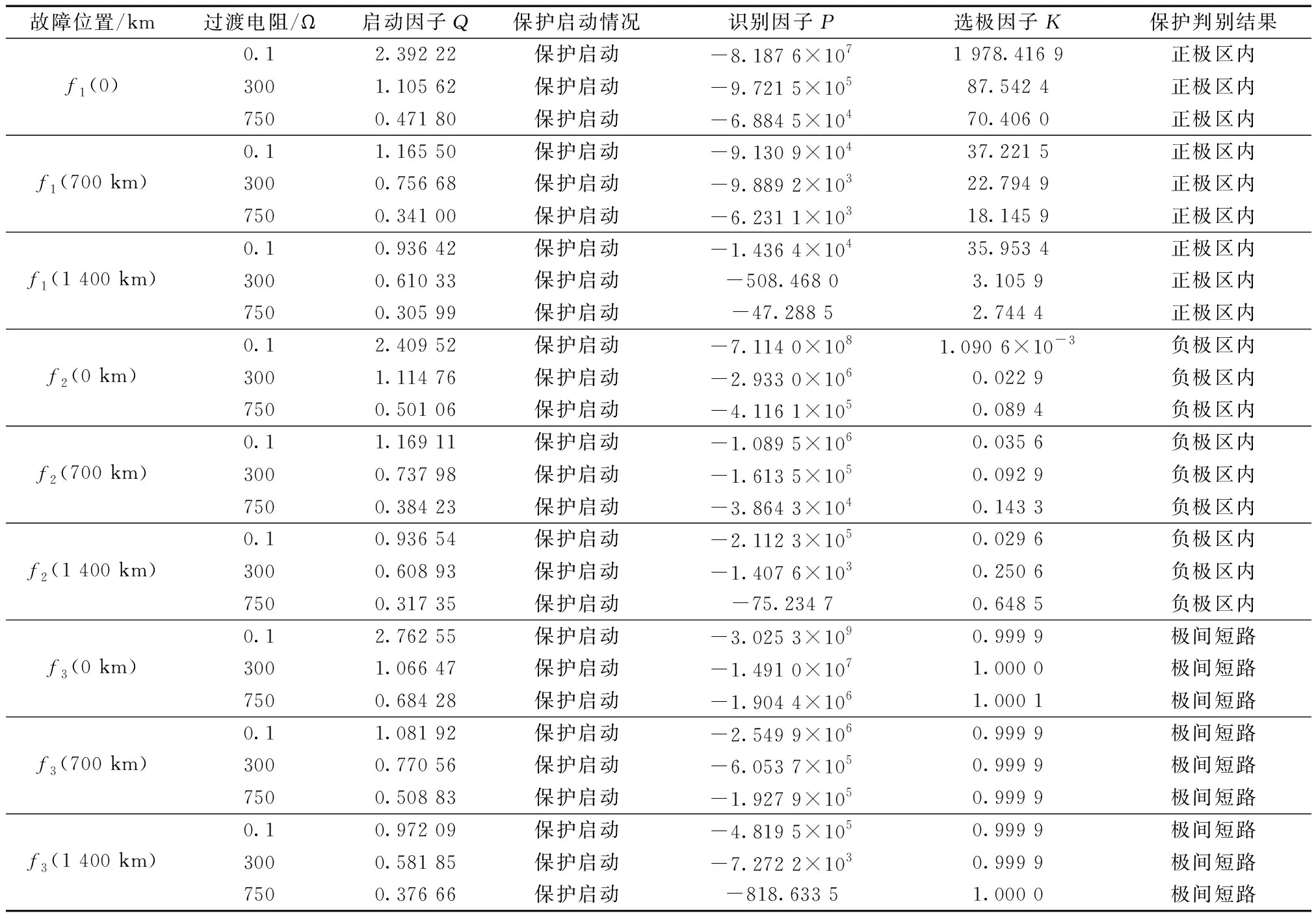
表2 区内故障仿真结果Table 2 simulation result of internal fault

表3 区外故障仿真结果Table 3 simulation result of external fault
(1)由于线路边界元件所具有的滤波特性,在直流线路区内和区外故障时,保护安装处的暂态电流550~650 Hz频带分量的幅值和波动情况具有明显的差异性。
(2)提出的利用切比雪夫数字滤波器获取频带电气量结合求熵值的方法提取故障特征,避免了对小波分析等时频分析方法的依赖,有效简化了算法。
(3)所提的保护方案可有效识别出各种直流线路区内外故障及故障极,并且在区内远端高阻接地故障情况下仍然具有较高的灵敏度,耐高阻能力达750 Ω,保证了保护动作的可靠性。
(4)在保护动作时间方面,所提的保护算法仅需10 kHz/5 ms数据窗,仅利用单端电气量,且算法计算简便,可满足保护对速动性的要求。
