线列式结构毁伤在弯曲载荷下的增益
2022-07-09舒张忆南梁争峰程淑杰阮喜军
舒张忆南, 梁争峰, 程淑杰, 阮喜军
(西安近代化学研究所, 西安 710065)
当今战场上导弹类快速空中目标的增加和飞机类常规空中目标的护甲强化对防空反导战斗部提出了更高的需求[1],最原始的大飞散角破片战斗部早已不能满足对空中目标进行有效毁伤的要求,因此在制导和引战技术水平发展的基础上,世界各军事强国都在发展定向战斗部等新型战斗部技术,其中聚焦战斗部就是定向战斗部的一种,能够将破片集中在很窄的一个范围内,大幅提高了战斗部的毁伤能力[2]。
而在聚焦战斗部的基础上,梁争峰等[3]提出了动态线列式破片战斗部技术,使破片呈线列式穿孔,更进一步提高了毁伤效果。并且结合设计原理给出了该类战斗部系统的设计方法和主要参数的计算公式,通过数值模拟和原理样机试验初步验证了方法的可行性。阮喜军等[4]利用数值模拟的方法对线列式战斗部的毁伤元进行了研究,提出了一种使用杆条作为毁伤元的新型线列式离散杆战斗部。对杆条的设计参数进行了理论计算和数值模拟,总结了各种参数的工程计算公式并验证了其正确性和可行性。王宝成等[5]则对线列式战斗部对导弹目标的结构毁伤效应进行了研究,并与聚焦战斗部的毁伤效果进行了对比。通过理论分析和数值模拟的方法得到了目标受载荷破坏时的最大应力和剩余强度,最终得出线列式破片战斗部对目标的结构毁伤效果优于聚焦战斗部的结论。
然而,上述研究只关注了导弹目标上线列式结构毁伤的效果,但是防空任务目标不仅仅只有导弹类目标,还有飞机类常规目标等,线列式结构毁伤对飞机类目标的毁伤效果研究还并不充分;而且仅仅采用了理论分析和数值模拟的方法,没有用试验结果来验证通过这些方法所得到的结论的有效性,这也是研究中需要完善的部分。
因此,为了研究线列式结构毁伤在弯曲载荷下的增益大小,设计模拟飞机类目标的平板结构等效靶标,并且在上面不同位置打孔来模拟结构受到线列式战斗部毁伤和聚焦式战斗部毁伤的不同情况。导弹、飞机等目标在空中飞行时会受到空气阻力与重力的影响,通常在这种情况下结构受到弯曲载荷的影响最显著。所以通过理论分析和数值模拟计算的方法来研究所设计的等效靶标在受弯曲载荷下的最大应力和剩余强度的差距,并使用弯曲静力学试验模拟毁伤目标在空中受载荷破坏的情况来验证理论分析和数值计算的结果,把线列式结构毁伤相对于聚焦式结构毁伤的增益进行量化比较。
1 线列式结构毁伤增益原理
破片杀伤战斗部对目标的毁伤效果与两个因素相关,一是破片穿孔造成的目标结构在穿孔处的截面面积减少,二是穿孔周围环向的应力集中现象[6]。这两种因素都会导致破片穿孔附近的应力增大,更容易达到材料屈服强度引起结构破坏。不过相比于战斗部毁伤目标的尺寸,破片穿孔造成的截面面积变化十分微小,对结构强度影响较小,因此破片穿孔的主要毁伤因素是穿孔附近的应力集中效应。
1.1 应力集中效应
从理论上分析孔周围的应力状态时,达到屈服前金属材料的弯曲可以视为弹性问题,在这种情况下结构的弯矩和扭矩可以由两个复变函数φ(z)和ψ(z)来表示[7],即
(1)
式(1)中:Mx、My和Hxy分别为单位长度的弯矩和扭矩;D为抗弯刚度;μ为泊松比;z为该点在复平面上的位置。复变函数φ(z)和ψ(z)需要由对象结构决定,比如在本文中研究含有N个相同大小圆孔的多孔平板结构时,可得到孔周在复平面上的参数方程zn为
zn=rcosθ+irsinθ+z0n
(2)
式(2)中:z0n为第n个孔的圆心坐标;r为圆孔半径;θ为孔周上的点到孔心连线与实轴的角度。
引进N个复变量ξn
(3)
根据文献[7]的推导,可以得到复变函数φ(z)和ψ(z)的表达式为
(4)
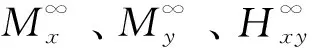
将式(4)和边界载荷条件代入式(1),经过推导计算后即可得到板内任意一点的弯矩和扭矩,进而可以得到孔边的切向和法向弯矩,以及对应位置的板内应力状态。
在研究应力集中效应时,可以分别计算只有单孔时和附近有其他孔的应力状态,从应力提高的幅度就可以判断应力集中效应的大小[8]。考虑受到固定大小弯矩的无限大平板,上面有两个相对孔距(孔心距离与孔径的比值)为2的圆孔时孔边的最大切向弯矩是单孔的1.05倍,而当相对孔距缩小到1.5和1.2时最大切向弯矩分别提高到1.12倍和1.32倍。可知应力集中现象受相对孔距影响,且在相对孔距减小的过程中应力提高幅度越来越大。
1.2 应力集中对破片穿孔结构毁伤的增益
因此,为了提高破片战斗部的毁伤效果,即提高破片穿孔后的应力集中效应,需要尽可能减小两个破片穿孔之间的间隙,在破片命中数相同的情况下,需要尽可能增大破片命中的密度,将破片穿孔汇聚在一个更小的区域内。对比聚焦式战斗部和线列式战斗部,控制相同的破片命中数,线列式战斗部的破片穿孔区域更小,所以两个孔之间的平均距离也更小,受相同载荷下孔附近的应力更大,更容易达到结构材料屈服强度,引起目标结构的解体破坏,能够更有效地造成结构毁伤。
2 数值模拟计算
分析推导孔附近的应力公式能够给出线列式结构毁伤优于聚焦式结构毁伤的理论支撑,然而实际情况下需要考虑到材料属性和破片穿孔状态,通过纯粹的理论计算来获取目标结构被破片战斗部毁伤之后的剩余结构强度较为困难,需要十分复杂的公式和大量的计算时间。因此要研究线列式结构毁伤的增益大小,就需要利用数值模拟软件来对实际受载情况进行模拟仿真。
2.1 设计等效结构靶标
破片战斗部毁伤的实际空中目标往往结构复杂,难以对其进行具体计算,需要进行简化,设计相对简单的结构体等效靶标来进行代替。飞机类常规空中目标相较于破片而言通常体积较大,破片的穿孔只能影响到其外壳的局部,此时可将外壳的结构近似为板状结构处理,用一块带孔平板来作为等效靶标模拟飞机类目标受破片毁伤后的外壳结构。
2.2 建立有限元模型
使用ANSYS/LS-DYNA有限元模拟软件来进行等效靶标受弯曲载荷的数值模拟计算,根据文献[9-10],靶标的材料选择常用于飞机、导弹等空中兵器装备蒙皮的2219-T62铝合金。
2219-T62铝合金的密度为2 840 kg/m3,弹性模量为73.8 GPa,泊松比为0.33,抗拉强度约为414 MPa[11-12]。平板结构的尺寸为长400 mm、宽300 mm、厚度为3 mm。在结构沿长度方向的中心打孔来模拟破片穿孔毁伤,对于线列式毁伤来说就是在结构中线上距离平均地打10个大小相同的孔,孔径为10 mm。聚焦式毁伤则是在结构中部取一定宽度范围的聚焦带,将相同数量的孔随机分布在这条聚焦带内,这里的聚焦带宽度取100 mm,即结构长度的1/4。
两种等效靶标结构如图1所示,材料使用J-C(Johnson-Cook)模型和Gruneisen状态方程,采用Lagrange网格划分[13],将结构两端固定,在中部施加随时间增加的位移载荷来模拟结构弯曲时的受载。

图1 两种等效靶标的结构示意图Fig.1 Schematic diagram of two equivalent targets
2.3 计算结果分析
经过计算后,结构在未发生破坏时、开始发生局部破坏时和加载完成时的沿长度方向的应力分布如图2和图3所示。
分析计算结果可知无论是模拟线列式毁伤的靶标(简称“线列式靶标”)还是模拟聚焦式毁伤的靶标(简称“聚焦式靶标”)都在孔附近出现了应力集中现象,且线列式靶标应力分布较为均匀,各个孔之间应力大致相等,然而聚焦式靶标上应力分布受孔的位置分布影响,孔间距离越小应力越大,与理论分析结果一致。当靶标未出现破坏时,在相同的载荷下,聚焦式靶标上除了距离极近的两个孔之间应力高于线列式靶标以外,其余大部分应力均小于线列式靶标。并且在逐渐提高载荷时,也是聚焦式靶标上两个接近的孔之间先发生破坏,不过其余部分发生破坏要晚于线列式靶标。加载完成后,线列式靶标已经近乎完全断裂,聚焦式靶标则只是沿孔密集的方向出现一条裂缝,并未完全断裂。

图2 线列式等效靶标应力分布图Fig.2 Stress distribution diagram of linear equivalent target
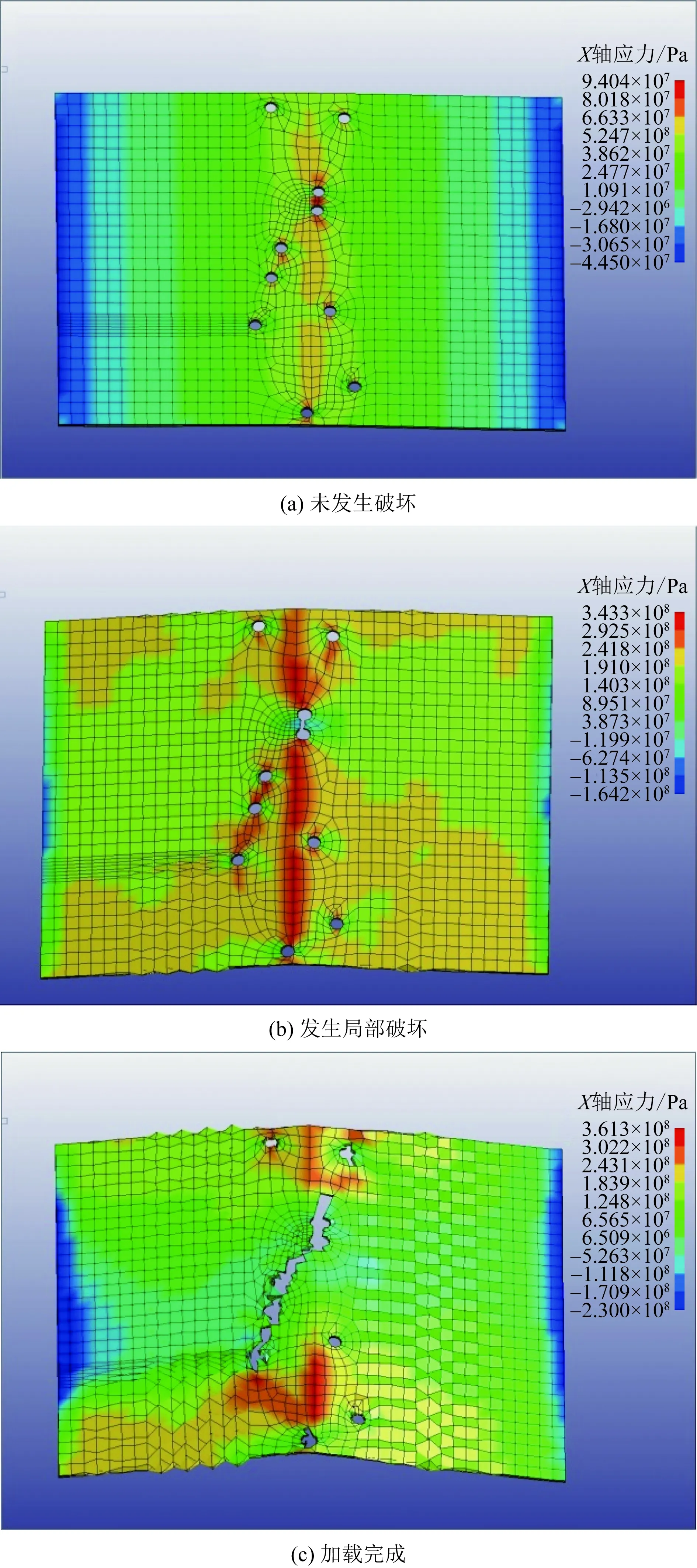
图3 聚焦式等效靶标应力分布图Fig.3 Stress distribution diagram of focused equivalent target
可以根据计算结果绘制出靶标上各点的应力-加载(时间)曲线,如图4所示。表1为取了靶标上几个点比较相同加载时间下的应力大小,根据计算结果可得,在发生破坏之前线列式靶标的最大应力比聚焦式靶标应力集中处平均高16%左右。
点1、2、3三条曲线取自孔间应力分布,点4和点5两条曲线取自其他位置。

图4 靶标内部应力-加载曲线Fig.4 Stress-loading curve in target

表1 未破坏时不同工况应力情况Table 1 Stress under different working conditions without failure
3 试验验证
为了验证数值模拟计算的可靠性,实际加工了和所设计的等效靶标结构相同的试件并对其进行静力学试验,通过应变片来获得试验中试件中的应力并与数值模拟计算的结果进行比较。
3.1 试验前准备
与数值模拟计算一样,用2219-T62铝合金加工制造相同结构的试件,并同时加工试验所需的连接工装夹具,试件照片如图5所示。
为了得到试验过程中结构上孔附近的应力,需要在指定位置贴上与试验机相连的应变片,通过将应变片接入电桥电路来得到应力数据。每个试件上前后两面相同位置各贴5枚应变片,一共10枚,贴应变片的位置如图6所示。

图5 试件照片Fig.5 Photo of specimen
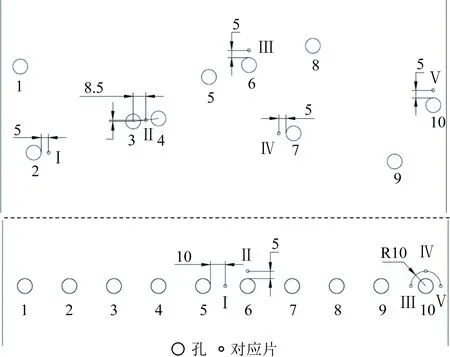
图6 应变片粘贴位置示意图Fig.6 Schematic diagram of sticking position of strain gauge
3.2 试验过程
试验所用的是单轴运动的力学试验机,由于在孔附近贴了应变片的关系,为了不影响到数据采集的过程,不能像数值模拟计算那样在采用三点弯曲法结构正中间进行加载,只能采用四点弯曲法,将试件固定在与试验机相连的下部夹具工装上,然后上工装随试验机从上方逐渐向下运动进行弯曲载荷的加载[14],如图7所示。

图7 试验过程Fig.7 Test process
3.3 试验结果与分析
试验结束后,试件的变形情况如图8所示,模拟受线列式结构毁伤的试件在孔间出现了较为明显的材料颈缩失效现象,而模拟受聚焦式结构毁伤的试件现象并不明显。

图8 试验后试件状态Fig.8 state of specimen after test
分析从应变片中得到的应力数据,可以绘制出如图9所示的结构未失效时应力随载荷变化的曲线。因为试件濒临失效时采集的应力数据不稳定,因此只绘制了结构未失效时的曲线,对应了图4中时间0~100 s的区间。从图9可知,图9中线列式试件上有3点应力较高,其余2点应力较低,这与图4中的结果吻合,而聚焦式试件上有3点应力较低,1点应力中等,而最后1点应力极高,也与图4中结果相符。试验结果与数值模拟计算的结果大致符合,验证了其有效性。在位移载荷达到26 mm左右时,线列式靶标试件应力曲线出现明显拐点,说明已达到屈服失效点,而位移载荷达到31.5 mm左右时聚焦式靶标试件的应力曲线才出现拐点,由此可计算得到线列式靶标试件达到屈服所需要的载荷相比聚焦式靶标减小了约18%。
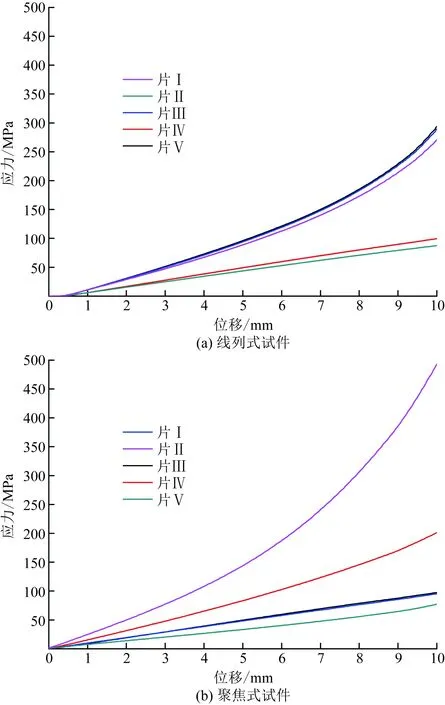
图9 结构未失效时应力-位移曲线Fig.9 Stress-displacement curve of structure without failure
4 结论
(1)对线列式战斗部的结构毁伤增益原理进行了理论分析,根据应力集中效应给出了线列式结构毁伤优于聚焦式结构毁伤的理论支撑。
(2)研究对飞机类目标的结构毁伤增益,分别设计了模拟线列式结构毁伤和聚焦式结构毁伤后的飞机外壳蒙皮结构等效靶标,并对这两种靶标在受相同弯曲载荷下的应力分布情况进行了数值模拟计算研究,得到了线列式靶标的最大应力平均比聚焦式靶标最大应力高16%的结论。
(3)加工相同工况的试件进行静力学实验,用试验结果验证了数值模拟计算的有效性,试验结果表明线列式靶标试件达到屈服所需要的载荷相比聚焦式靶标减小了约18%。
