利用能级交叉和二聚化算符表征海森堡反铁磁系统的量子相变

李童欣，揭泉林，王 伟

武汉大学物理科学与技术学院，湖北武汉430072

0 引言

学者们对二维方格子阻挫自旋1/2海森堡模型的研究兴趣源于高温铜基超导体的提出［1］。阻挫的反铁磁耦合对可以形成自旋液态（spin liquid，SL）［2～5］，比如共振价键态（resonating valence bonds，RVB）［4，6～8］可以通过掺杂的方式转变为超导态。海森堡模型作为一个二维系统原型，无论是在理论研究还是数值计算领域都具有很重要的意义。特别是顺磁相中精细的量子相变，它的本质仍在广泛讨论中，引起了许多研究者的参与兴趣［7，9～17］。

该模型中间相的形成有多种猜想，比如可能是由于自旋单态、共振价键体或是自旋液态引起的格点体系自发对称破缺导致的，进而推测中间相可能存在栅格态（columnar dimer）、块价键体、有能隙或者无能隙的自旋液态［4～6，17］。该模型目前最新的研究表明，中间相可以分成两个结构不同部分，并且中间可能存在无能隙的自旋液态相将这两个部分分开，而不仅仅是一个相变点［4，6，17］。

受限于尺度效应，目前中间相很多问题都处在争议和讨论之中。一些数值方法本身引入的一些先入为主的设定，也是进一步深入理解中间相本质的很大障碍。虽然目前没有一个天才的方法可以一次解决该模型所有方面的问题，但对于特定的方面，可以找到相适应的方法进行有效的研究。一个相当不错的方法就是，通过数值方法计算能级或能谱来确定中间相内精细相变的位置。由于能级交叉点对尺度的依赖是平滑的，可以较可靠地外推到热力学极限［10，12，14，15，17］。

为了确定体系结构，聚合化算符［6～10，12，13］也是一个实用且有效的工具。二聚化算符是最简单的结构化算符，涉及的格点数最少，而且它是一个标量，可以很方便地用来确定中间相的二聚化结构成分。

本文主要研究周期性边界条件下阻挫自旋1/2海森堡反铁磁J1-J2方格子的基态和低激发态。根据能级交叉和二聚化算符，确定中间相的相变点和能态结构，并寻找自旋液态。本文组织如下：第1部分报道能态计算、能级交叉，还有忠实度、磁结构因子、磁化强度和自旋关联等，给出相应的相变点位置；第2部分通过结构化算符表征自旋液态结构。

1 基本能态结构

二维海森堡模型是一个典型的多体问题，其哈密顿量可以写为

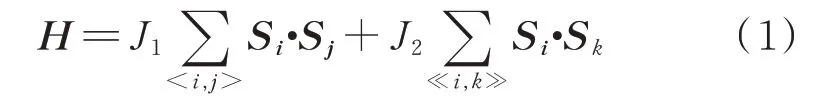
式中所有记号全部按照约定习惯：Si是格点i处自旋1/2算符；对＜i，j＞和≪i，k≫的求和分别对最近邻（nearest-neighbor，NN）和次近邻（next-nearestneighbor，NNN）进行，格点间每个键计算一次。为简便计，取J1为单位1，反铁磁模型下J2＞0为耦合参数，或者取无量纲数g=J2/J1作为耦合参数。

对于格点数N=16的方格子体系，通过正交化波算符［17］配合迭代法，得到体系的基态和第一激发态，发现在激发态出现能态简并。为了处理简并能态，进一步通过三分法和共轭梯度法进行逆迭代，在低激发态能级间作地毯式能量扫描，确定体系的能级结构。然后在本征能量下用逆迭代计算过完备的基矢组，利用正交化方法取总自旋量子数S子空间正交完备基，将总自旋z分量在S子空间中精确对角化，得到哈密顿量H、总自旋量子数S、总自旋z分量量子数的共同本征态。

依据参数g划分能态，计算结果通过表1给出。基态GS全部为单态；第一激发态LEV 1在0.41处分开成两个部分，0.00～0.40的区域属于自旋三重态，0.41～0.99的区域属于自旋单态；第二激发态LEV 2将LEV 1的两个区域进一步分成5个更精细的区域，0.00～0.21属于自旋五重态，0.22～0.40属于自旋单态，0.41～0.49属于自旋三重态，0.50～0.71属于自旋单态，0.72～0.99属于自旋三重态。特别地，根据Z2几何自旋液态的拓扑二重简并特征［3，5，17］，发现在LEV 2中区域0.50～0.52存在两套简并的自旋单态相互正交，以它为基矢可以形成一个二维流形，流形上的每一个态都是自旋单态，它很可能就是将中间相分成栅格态和块价键体［18］的Z2自旋液态；区域0.72～0.99存在两套简并的自旋三重态，它则是由于条纹相在激发态C4自发对称破缺的消失造成的，条纹不再自发选择x或z方向中的一个，而是都有可能且可以任意叠加。

表1 基态和低激发态能级L的总自旋量子数与简并度D对参数g空间的划分Table1 Quantum spin numbersand degeneracies D of ground states and low-lying excitations:a partition in parameter g space

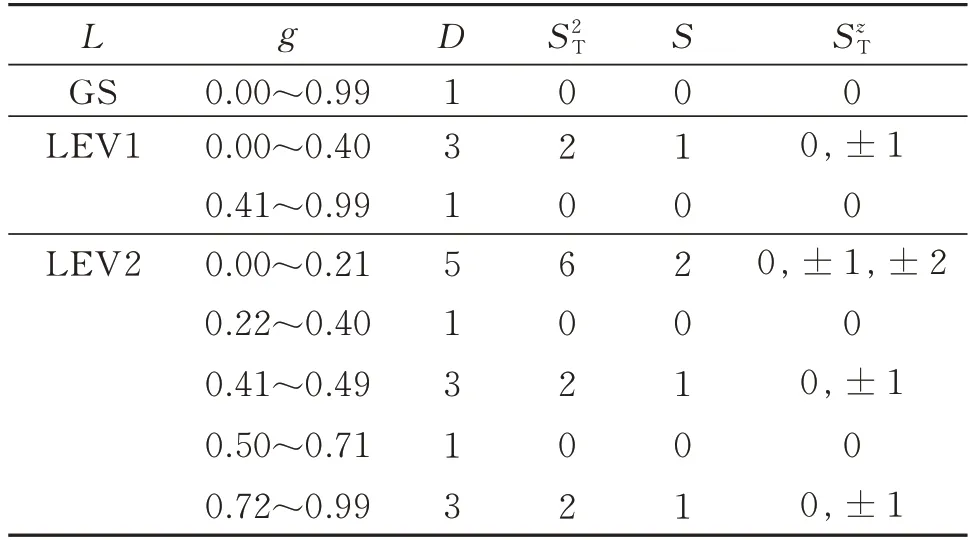
表1 基态和低激发态能级L的总自旋量子数与简并度D对参数g空间的划分Table1 Quantum spin numbersand degeneracies D of ground states and low-lying excitations:a partition in parameter g space

格点数N=16体系的两个自旋单态和一个最低的自旋三重态相对于基态的能隙随着无量纲参数g的变化过程在图1中进行了展示。自旋单态E1(S=0)和三重态E1(S=1)在临界点gc1=0.41的位置发生交叉，如图1(a)所示，而自旋单态E2(S=0)和三重态E1(S=1)在临界点gc2=0.71的位置发生交叉，如图1(d)所示，由gc1和gc2之间的区域给出中间相的位置。在中间相区域，自旋单态E1(S=0)相对基态的能隙随着g的增加衰减很快，如图1(a)中对应的曲线E1(S=0)所示。自旋单态E2(S=0)与三重态E1(S=1)在临界点gcin1=0.49发生交叉，如图1(b)所示，并在gcin2=0.53的位置发生交叠，图1(c)所示，这两个临界点将中间相分成三个精细区域。在图1(b)中两曲线交叉点的右侧，区域g=0.50～0.52有两组简并的自旋单态，可能是具有二度拓扑简并的自旋液态相，而在g=0.53～0.71的区域只有无简并的自旋单态。

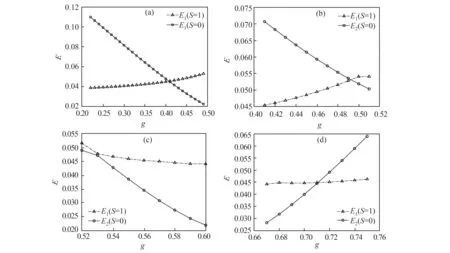
图1 低激发态能级交叉，相对于基态的能量E以J1为单位(a)最低激发自旋单态E1(S=0)与最低激发自旋三重态E1(S=1)的能级交叉，(b)次低激发自旋单态E2(S=0)与最低激发自旋三重态E1(S=1)在中间区域的能级交叉，(c)次低激发自旋单态E2(S=0)与最低激发自旋三重态E1(S=1)中间区域的能级交叠，(d)次低激发自旋单态E2(S=0)与最低激发自旋三重态E1(S=1)的能级交叉Fig.1 Low-lying level crossing,where the energies E relative to ground states are of unit J1(a)Level crossing between the lowest excited spin singlet E1(S=0)and the lowest excited spin triplet E1(S=1),(b)Level crossing between the second lowest excited spin singlet E2(S=0)and the lowest excited spin triplet E1(S=1)in the intermediate region,(c)Level overlap between the second lowest excited spin singlet E2(S=0)and the lowest excited spin triplet E1(S=1)in the intermediate region,(d)Level crossing between the second lowest excited spin singlet E2(S=0)and the lowest excited spin triplet E1(S=1)

在中间相区域，自旋液态相的左边和右边分别是栅格态和价键体。需要说明的是，低激发态可以反映基态的性质［14，17］，并且基态相变可以通过给定总自旋量子数子空间内部或者不同总自旋量子数子空间正交化能级间的交叉来表达。根据这种交叉模式，在热力学极限下，分别可能出现三种情况，如图2所示：(a)无能隙的自旋液态［4］，上下能级有一个重叠的平台；(b)无能隙的一个临界点［18］，上下能级的顶点重叠；(c)有能隙的自旋液态［5］，上下能级的谷峰位置有一段重叠区域。

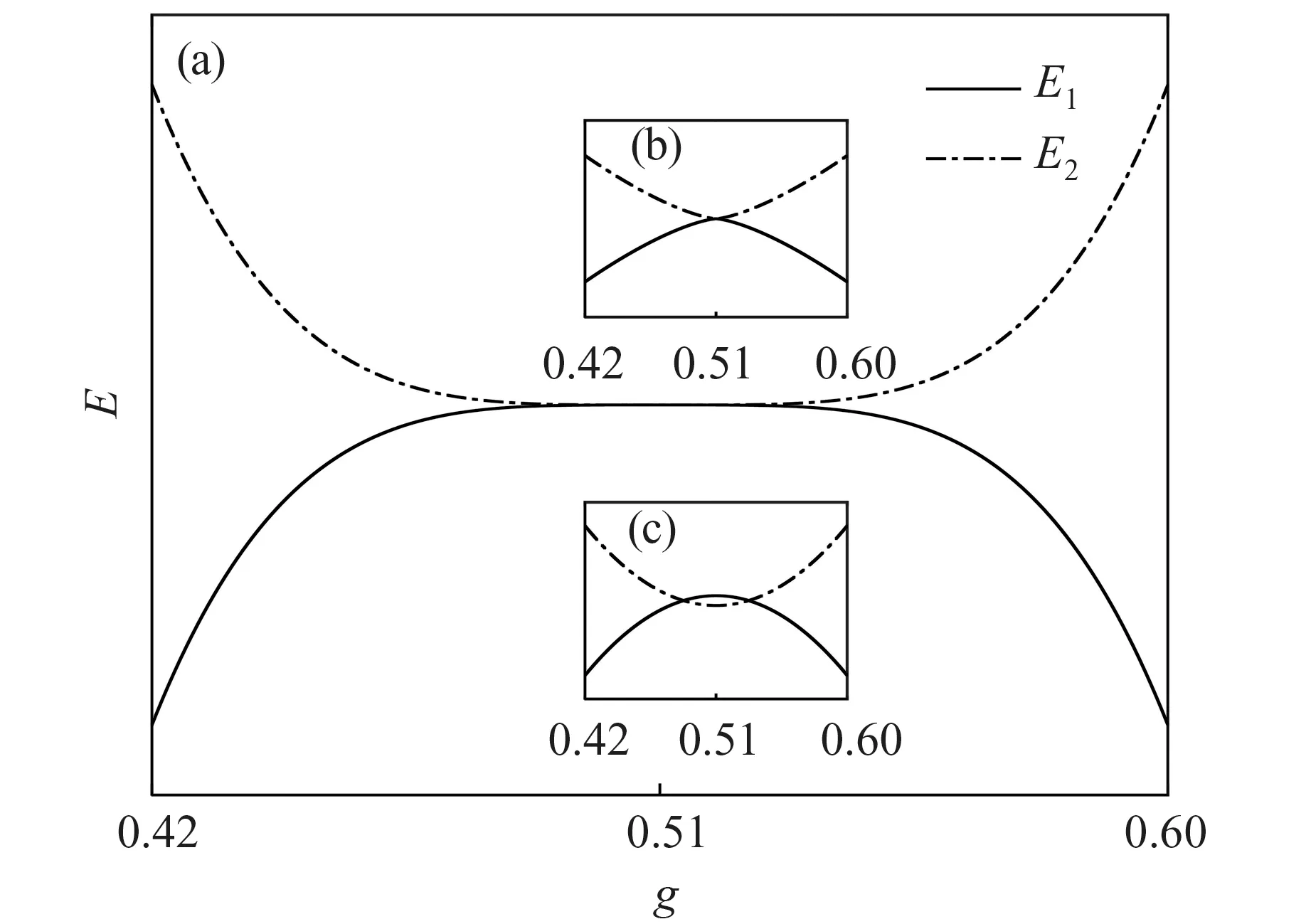
图2 热力学极限下中间相内部可能出现的能级交叉模式(a)无能隙的自旋液态，(b)无能隙的一个临界点，(c)有能隙的自旋液态Fig.2 Probable level crossing modes in the intermediate region in the thermodynamic limit(a)A regime of gapless spin liquid,(b)A critical point of gapless spin liquid,(c)A regime of gapped spin liquid

图1中能级交叉是从能量角度给出的，还可直接从量子态角度考虑，利用基态及低激发态的忠实度［19］

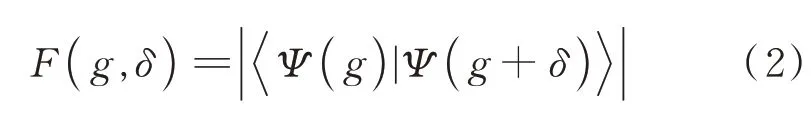
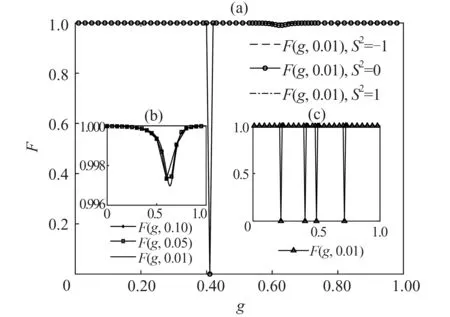
图3 基态和低激发态的忠实度(a)第一激发态LEV 1，(b)基态GS,(c)第二激发态LEV 2Fig.3 The fidelity of ground state and low-lying excitations(a)1st excitation LEV 1,(b)Ground state GS,(c)2nd excitation LEV 2

对于中间相与Neel相和条纹相之间的相变点，其他研究者用不同的处理方法进行了计算。簇耦合方法（coupled cluster method，CCM）给出gc1=0.454，gc2=0.588［16］，有限尺度精确对角化方法给出gc1=0.40，gc2=0.65［10］，Lanczos精确对角化方法给 出gc1=0.35，gc2=0.66［14］，密度矩阵重整化群（density matrix renormalization group，DMRG）给出gc1=0.41，gc2=0.62［5］，蒙特卡洛（Monte Carlo，MC）给 出gc1=0.4，gc2=0.6［4］。本文的结果gc1=0.41与其他方法的结果相近，说明通过第一与第二激发态的能级交叉可以较好地反映二级相变点的位置，而gc2=0.71与其他方法的结果出入比较大，说明当有限尺度下基态与第一激发态能级交叉没有表现出来时，用第二和第三激发态的能级交叉来指示一级相变点，存在较大的尺度依赖性。

对于中间相内的精细相变点，簇耦合方法给出gcin1=0.49，gcin2=0.58［16］，蒙特卡洛方法只识别出一个相变点gcin1=0.50［4］，密度矩阵重整化群方法识 别 出gcin1=0.46，gcin2=0.52［5］。本文的结果gcin1=0.49，gcin2=0.53所能确定自旋液态区域相比其他方法要小，而且在N=16体系下表现为能隙很小的Z2自旋液态。中间相内的相变是目前争议最大的问题，不仅对相变点的位置有所保留，甚至中间相有没有自旋液态，自旋液态有没有能隙都在激烈的讨论中。产生这些分歧的主要原因是计算体系的尺度不同，以及伴随处理这些体系近似方法的差异。本文计算的是有限尺度N=16下体系表现出来的特征，并进一步计算了N=18和20尺度下能级交叉表现出来的趋势。

采用Marshall-Peierls态比重方法［11，14］，计算了基态在三个样本态g'=0.00，0.50，0.99上的投影大小SW，并在图4中作出了三条对应的态比重SW随参数g变化的曲线。发现反铁磁Neel态g'=0.00在g＜0.50的区域维持着很高的比重(＞80%)，在g=0.50～0.60的区域Neel态的比重随着g的增大迅速衰减，当g到达0.71的时候Neel态的比重已经很低(＜20%)。相反，条纹态g'=0.99在g＞0.71的区域维持着高比重(＞90%)，在g=0.50～0.71的区域条纹态的比重随着g的减小迅速衰减，当g＜0.50的时候条纹态的比重已经非常低(＜10%)。特别地，自旋液态g'=0.50的比重在g=0.5附近达到峰值，往左随着g的减小自旋液态的比重逐渐衰减到80%以下，而往右随着g的增大自旋液态的比重迅速衰减到20%以下。

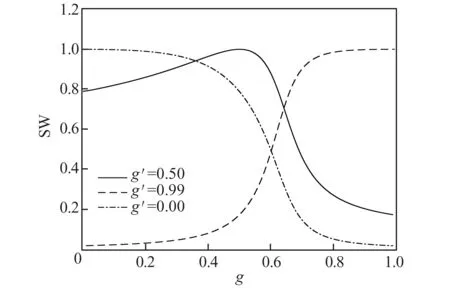
图4 Marshall-Peierls态比重方法成分分析样本态g'=0.00,0.50,0.99在基态中的比重SW随参数g的变化Fig.4 Component analysis by Marshall-Peierls state weight method State weights(SW)of the states sampled at g'=0.00,0.50,0.99 in ground state versus parameter g

在给定量子态下，对于总自旋量子数S，对应总自旋算符的平方可以表示为

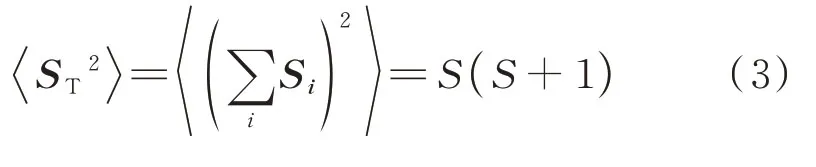
以及总自旋算符z方向分量为

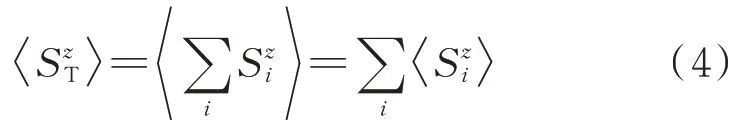
两个自旋格点间的关联函数可以表示为Cij=根据哈密顿量的表达式，能量可以通过自旋关联表达出来

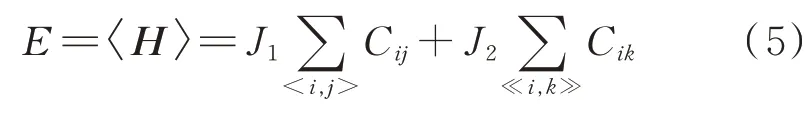
因为该模型中能量的本质就是自旋在两种耦合模式下的关联相互作用，所以能级交叉也可以通过自旋关联的交叉来反映，如图5所示。对于基态，自旋关联的值随距离平方的增加震荡衰减，如图5(b)所示，进一步作出自旋关联的绝对值随着距离的变化曲线，如图5(c)所示，基本上呈指数衰减。在参数g空间中，自旋关联的交叉给出临界点，如图5(a)所示：最近邻r2=1与次近邻r2=2的自旋关联交叉于=0.63的位置，给出一阶相变点的位置，这与其他方法［4，5，10，14，16］给出的一阶相变点比较吻合；阻挫相互作用下，在相变点的左边Neel序占优，而在相变点右边条纹序占优；该体系中最远关联r2=8与次远关联r2=5有两个交叉点gcin1=0.49和在临界点gcin1处两种关联均接近于零；在r2=8与r2=5谷峰交叠区域的左侧g＜gcin1，二者基本上等大反号，而在右侧g＞随着g的增大，次远关联r2=5的数值很平滑地趋于零，最远关联r2=8反而较快地增长到超过g=0.00时的水平；次近邻r2=2与次远r2=5的自旋关联在临界点gcin2=0.54处发生交叉，在交叉点gcin2的左侧，随着g的增大，中程r2=4与次近邻r2=2的自旋关联一致地下降，而在交叉点的右侧中程r2=4自旋关联不降反升，与最远关联r2=8保持一致。

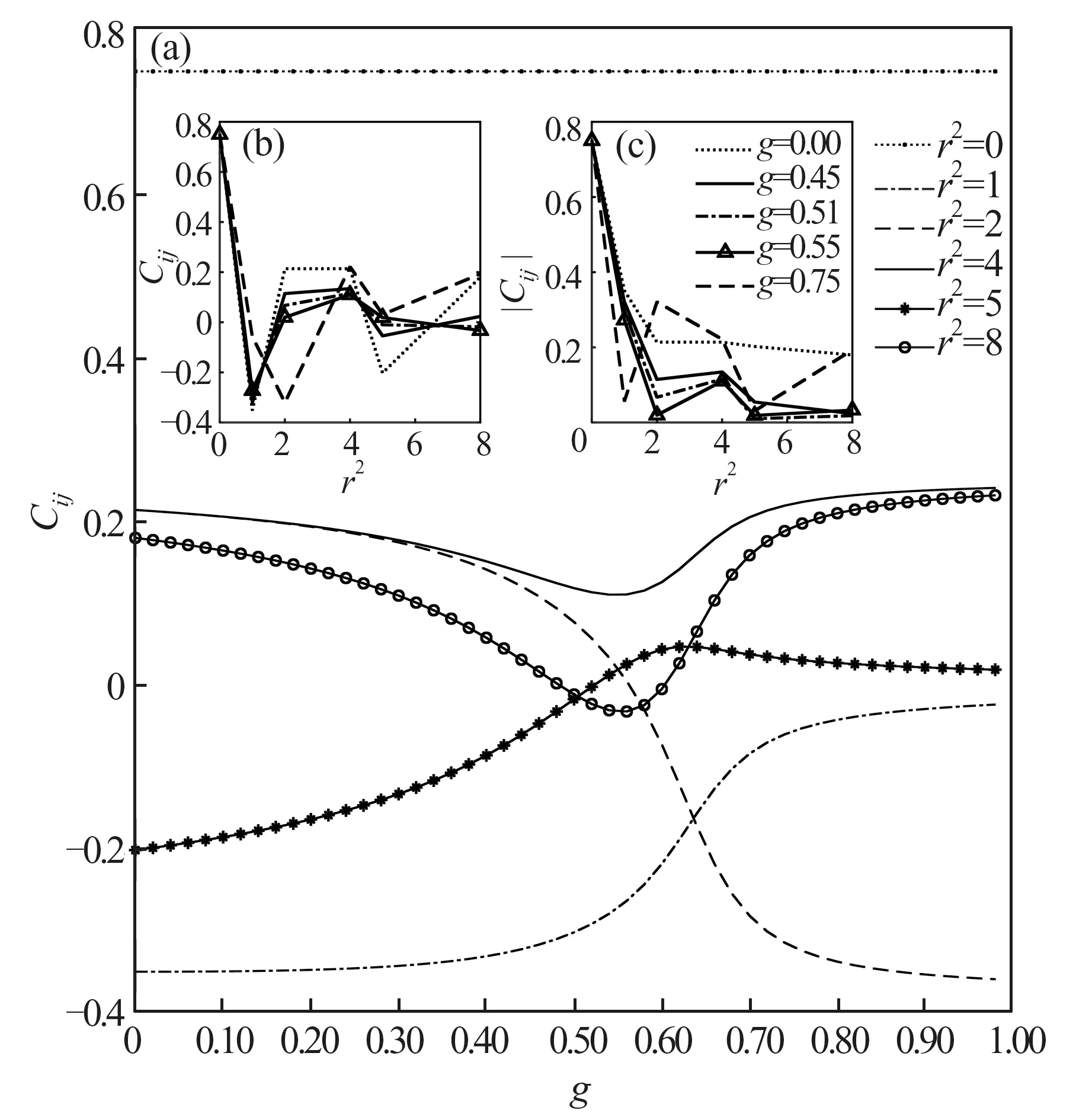
图5 自旋关联(a)自旋关联Cij随参数g的变化，分别给出6条不同关联长度平方r2下的关联函数曲线，(b)自旋关联Cij随关联距离平方r2的变化，(c)自旋关联的绝对值|Cij|随关联距离平方r2的变化，分别给出5个特征g值下的曲线Fig.5 Spin correlation(a)The curves of spin-correlation function Cij versus g for 6 different correlation length's square r2,respectively，(b)Spin-correlation Cij versus r2，(c)Absolute value of spin-correlation|Cij|versus r2 for 5 typical values of g

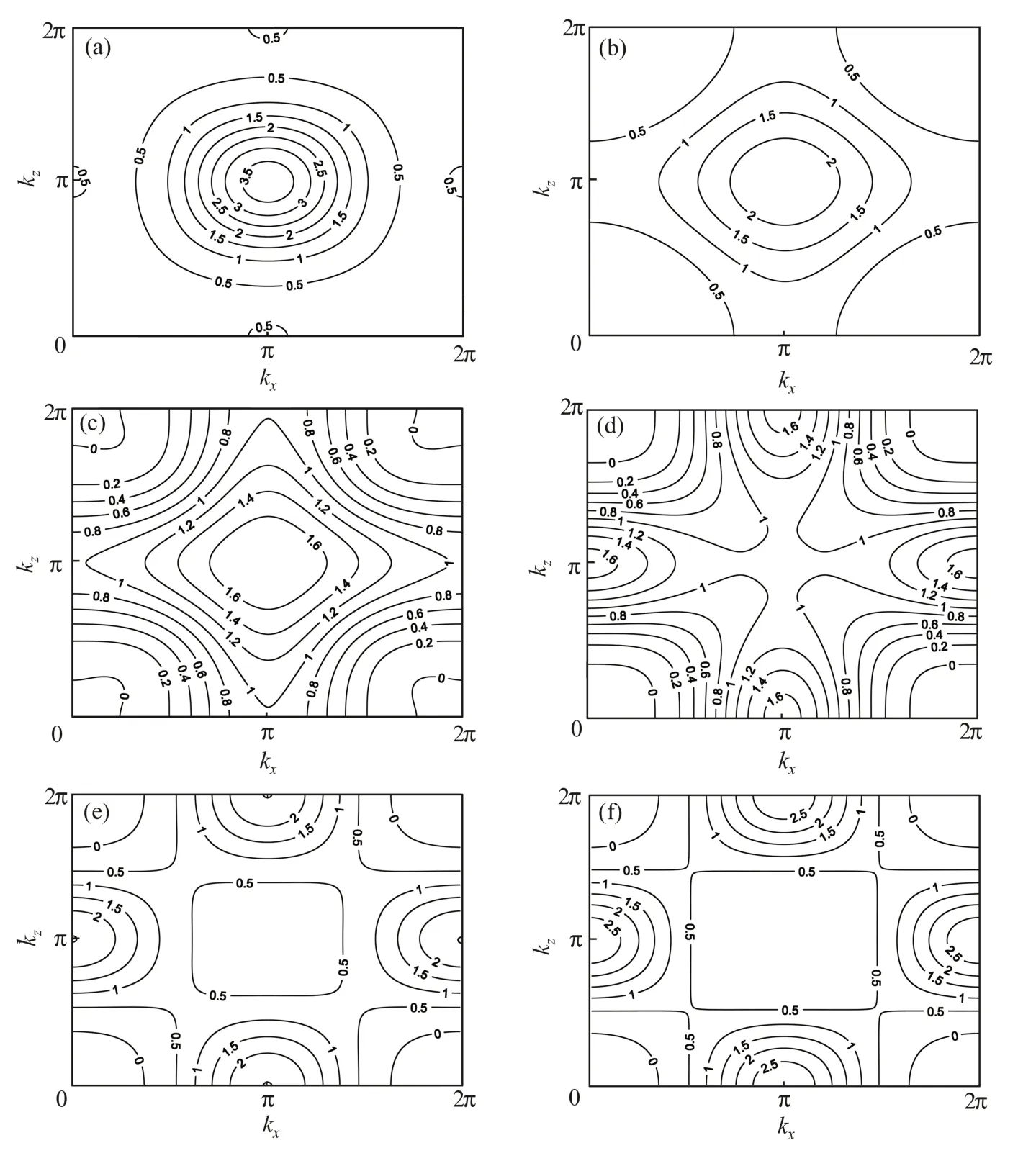
图6 特征参数g=0.30,0.51,0.57,0.63,0.71,0.99值处结构因子等高线的峰谷和鞍点位置(a)g=0.30,(b)g=0.51,(c)g=0.57,(d)g=0.63,(e)g=0.71,(f)g=0.99Fig.6 Peak-valleys and saddle points of structure factor contour maps at typical parameter value g=0.30,0.51,0.57,0.63,0.71,0.99(a)g=0.30,(b)g=0.51,(c)g=0.57,(d)g=0.63,(e)g=0.71,(f)g=0.99

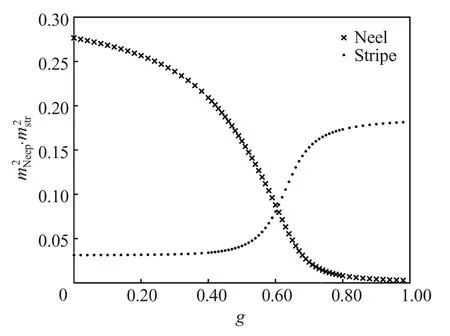
图7 Neel序和条纹序的磁化强度Fig.7 Magnetization of Neel and stripe phases

通过计算基态能量及其对参数g的一、二阶导数，如图8(a)所示，基态能量在中间相达到极大值，能量的一阶导数在=0.63处有一个陡峭的下降，能量的二阶导数在处有一个极小值，对应一阶相变点。在热力学极限下基态能量在处不连续，所以是一个在有限体系下没有显现出来的基态能级交叉点。图8(b)给出N=16体系的基本能级结构和能隙，可以看到各能级间的交叉以及能隙的零点位置。第一激发态相对于基态的能隙在gc2附近达到极小值接近于零，而且基态能量相对于参数g的二阶导数在处给出一个极小峰，这两个点给出了有限尺度下一阶相变点可能存在的大致范围根据分级平均场［20］和簇密度矩阵内嵌［21］得到热力学极限下临界点附近基态能量不解析，蒙特卡洛方法［4］得到临界点附近存在块价键态和条纹态的能级交叉，表明此处发生的是一阶相变。图9通过计算N=18，20这样更大体系的能级发现，当体系到达20个格点的时候，就可以比较准确地看到一阶相变的能级交叉。

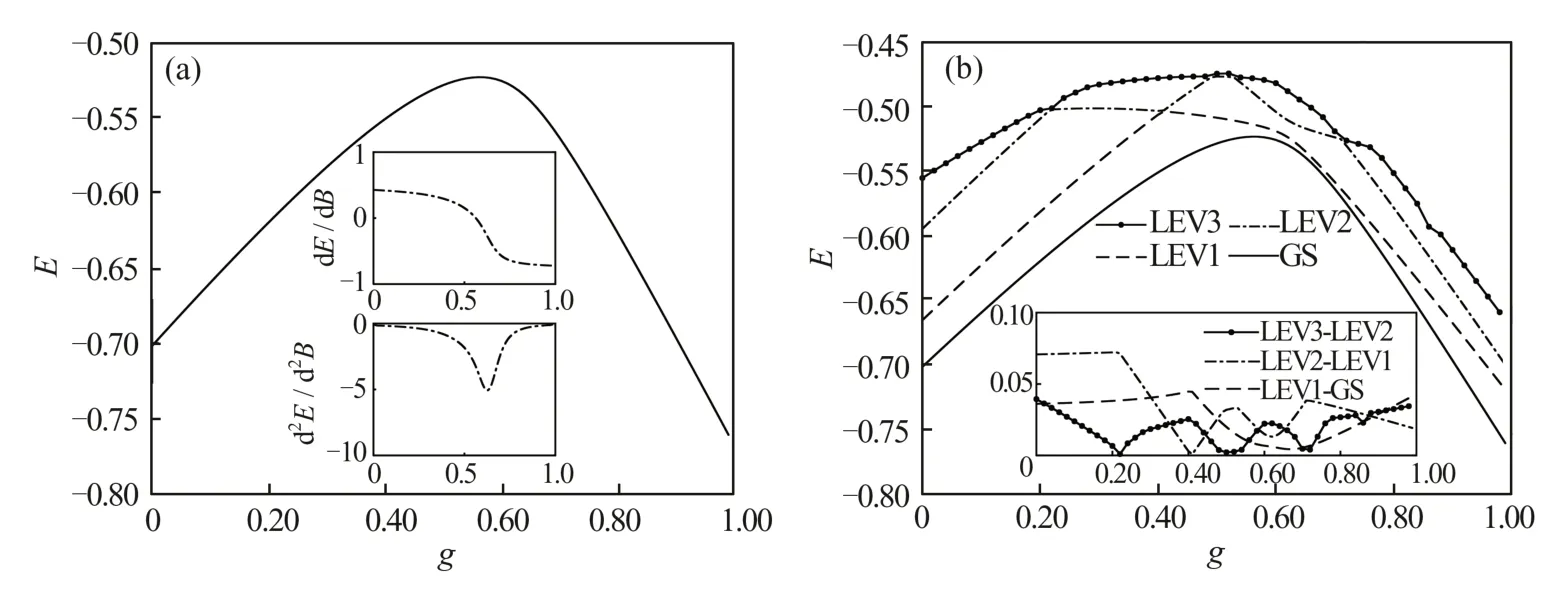
图8 N=16体系的能量(a)基态能量（主图）及其一、二阶导数（子图），(b)基态低激发态能级（主图）和对应的能隙（子图）Fig.8 Energy of the system N=16(a)Ground-state energy(main plot)and corresponding derivatives to 2nd order(2 subplots)，(b)Ground state and low-lying energy levels(main plot)and corresponding gaps(subplot)

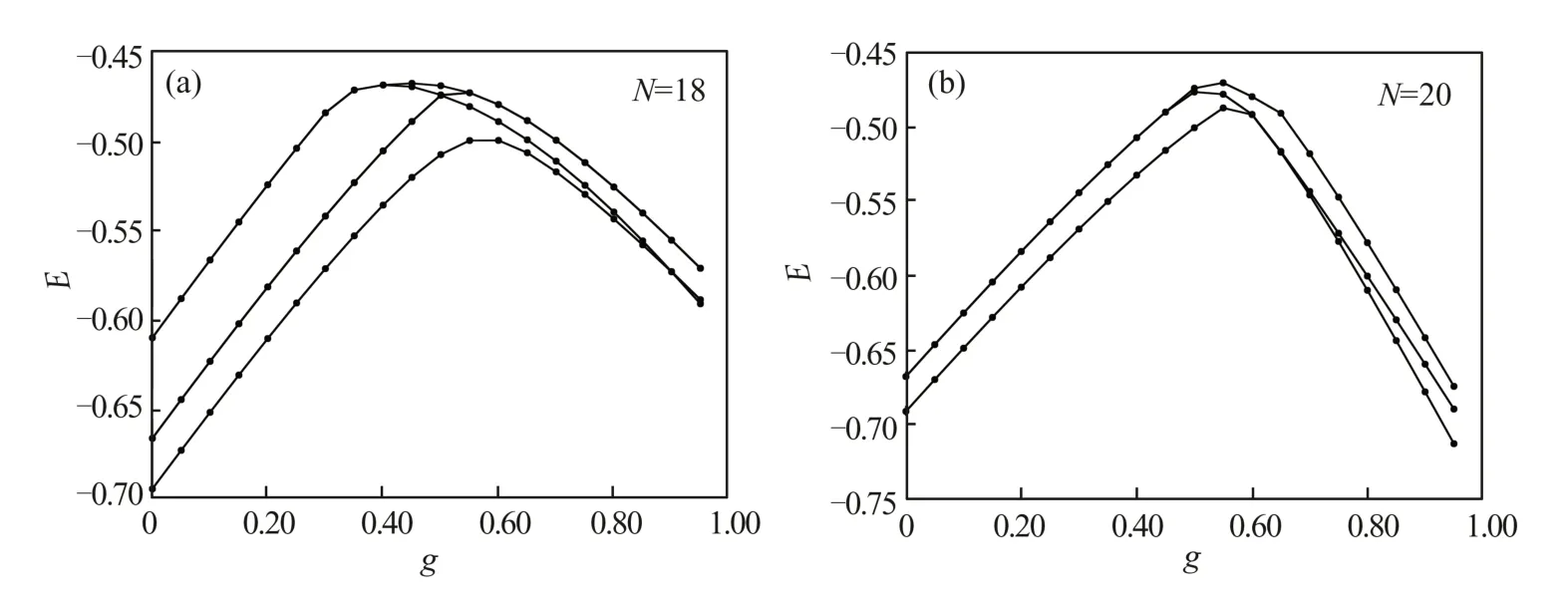
图9 尺度为N=18,20体系的基态和低激发态能级Fig.9 Ground state and low-lying energy levels of systems with size N=18,20

本文使用的计算工具是第一作者自主编写的C程序：迭代算法的核心是抽象算符作用和矢量化，避开存储超大型矩阵（232个双精度矩阵元，对于N=16体系），哈密顿量的作用过程通过独立的翻转逻辑函数来实现，翻转操作对象为数组化的态矢量；逆迭代算法的核心是共轭梯度法，对于海森堡模型中算符两两作用的二次收敛问题，其精度和计算效率十分可靠。基于共享的原则，作者将整个程序包放在ResearchGate科研意识形态网站（https：//w w w.researchgate.net）上开放阅读交流。

对于计算效率，一般精度模式下每个能态的计算耗时3分钟，高精度模式下每个能态的计算耗时1小时。一般精度模式主要用于三分法中对能级作地毯式扫描，精确计算能态则要用到高精度模式。

2 中间相结构的表征

由于相互作用的传递，不仅不同距离的格点某种程度地关联起来，而且一些格点簇也会呈现出关联，进而产生不同的局域化结构。二聚化算符［4，5］可以定义为一种沿着ζ=x或z方向的键作用算符是一种最简单的结构化算符，并且是一个标量，使用十分方便。类似于用自旋算符描述自旋关联一样，同样可以利用二聚化算符描述格点簇的二聚化关联

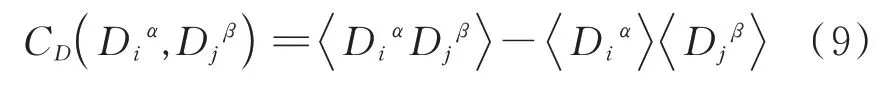
类比自旋格点的结构因子，还可以构造二聚化结构因子［4，17］

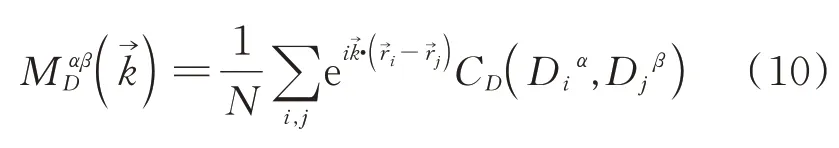
取x方向二聚化得到格点簇的聚合强度

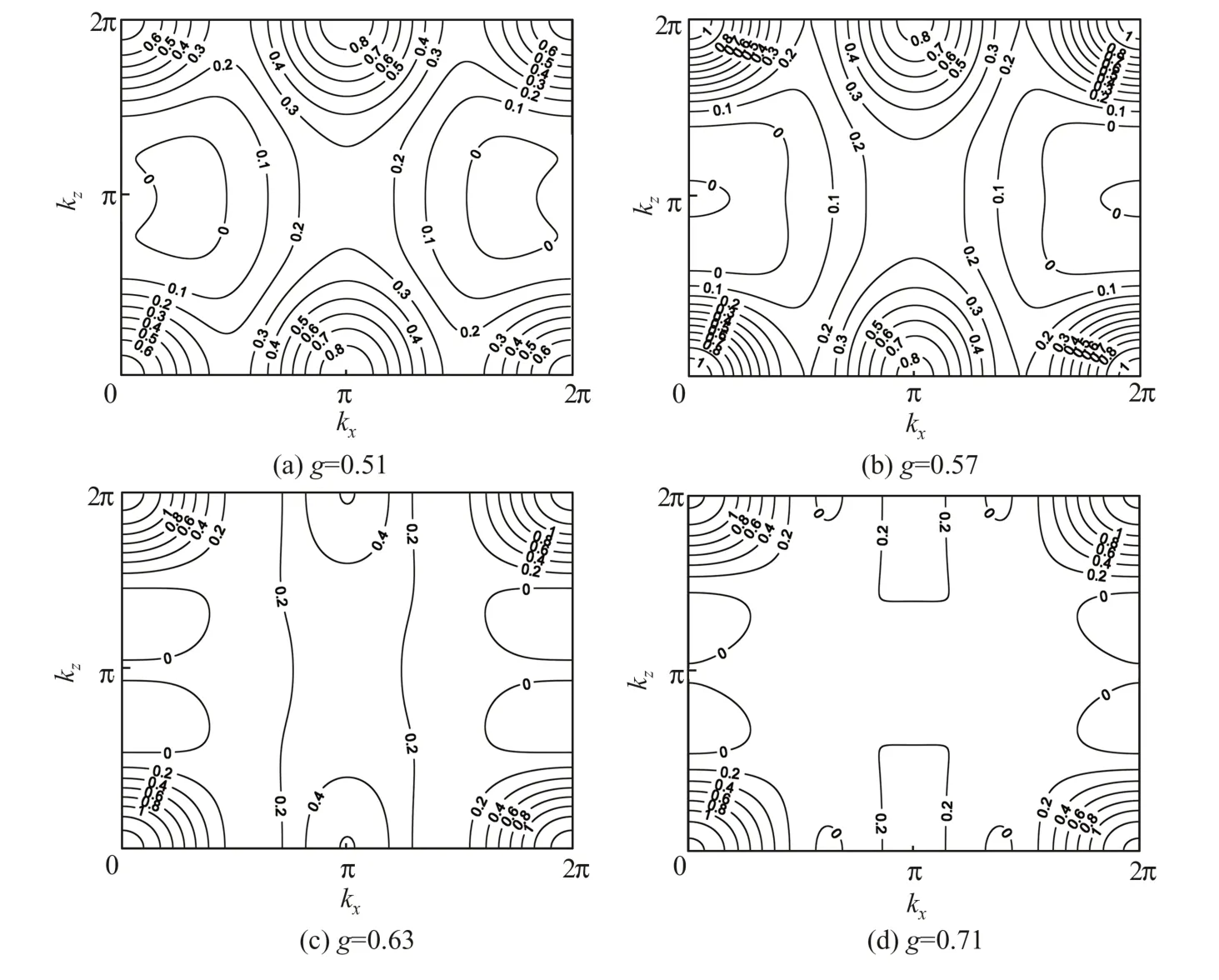
图10 特征参数g=0.51,0.57,0.63,0.71值处的二聚化结构因子等高线的峰谷和鞍点位置Fig.10 Peak-valleys and saddle points of dimer-structure factor contour maps at typical parameter values g=0.51,0.57,0.63,0.71

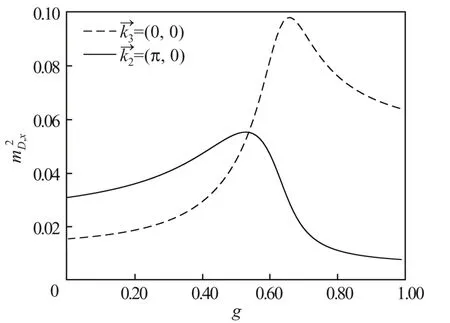
图11 二聚化格点簇聚合强度Fig.11 Aggregation intensity of dimers

3 结语

考虑到格点系的哈密顿量H(g)是无量纲参数g的函数，我们追踪H(g)的基态能量随着g的演化函数。对于有限体系，基态能量对参数g是光滑的、解析的。出现违反这一规则的情况，主要是由于g耦合了两个相互对易的部分。在给定g的邻域内，当近邻项H0和次近邻项H1变化不大时，能量曲线在该g值附近可以近似用一个切线来拟合，其中分别是与H0和H1相关的常数参量。通过体系总自旋量子数可以看出，虽然本征能量随着g改变，但是本征函数却和g无关，这样便会出现能级交叉。一个激发态在这个临界点同时也是基态，这种交叉破坏了基态能量对g的解析性，形成奇异点。由于哈密顿量是对一个体系相互作用的一般描述，所以不仅仅是基态能量，低激发态能量对g的解析性也会由于能级交叉的出现而产生奇异点。

一个在有限体系下没能表现出来的能级交叉，随着格点体系的增大，能级交叉将会越来越显著，最后在无限大体系下形成一个尖锐的临界点。热力学极限下，我们可以找出任何基态能量不解析的奇异点。这些点就是体系的量子相变点，它们可以是有限体系下已经出现的能级交叉点，也可能是有限体系下没有表现出来的能级交叉点。

本文计算了自旋1/2海森堡反铁磁J1-J2方格子的基态和低激发态及相应的本征能量，并在总自旋量子数S子空间内精确对角化，进一步得到哈密顿量H、总自旋量子数S、总自旋z分量量子数Sz的共同本征态。根据能级交叉和二聚化算符，近似给出中间相内的相变点gcin1=0.49和gcin2=0.53。计算结果表明，在中间相g=0.41～0.71的左右两侧分别为Neel相(g=0.00～0.40)和条纹相(g=0.72～0.99)；中间相被低激发的自旋单态S=0和自旋三重态S=1的能级交叉分隔成了g=0.41～0.49和g=0.50～0.71两个区域，并且在g=0.50～0.52的区域发现低激发态拓扑二重简并的Z2几何自旋液态。