基于熵权法和组合隶属函数的雷达质量评估方法研究

朱常安，胡文华，郭宝峰，薛东方，尹园威

(1.陆军工程大学 石家庄校区，石家庄 050003; 2.中国人民解放军61035部队，北京 100094)

0 引言

根据军事百科全书中的相关定义，装备质量是指“装备的固有特性满足要求的程度”，其固有特性分为功能特性和保障特性。功能特性主要有机动性、防护能力、火力、通讯能力等；保障特性主要包括可靠性、维修性、保障性、测试性和安全性等。对于不同类型的装备有不同的研究角度，其质量也有不同的具体内涵[1]。近年来，随着复杂装备的系统集成化、操控信息化的程度越来越高，对其操作使用和保养维修提出了更高的要求，因此，准确评价其质量状况具有重要意义[2]。雷达作为航空航天领域的“千里眼”“顺风耳”，具有目标探测、侦察预警、导航跟踪等强大功能，是现代化武器系统的重要组成部分[3]。对雷达系统进行质量评估，能够为雷达设备的生产研发、性能改进提供数据支撑，为使用和维护雷达装备提供科学依据[4-5]。关于复杂装备质量评估的研究方法比较多，大致可以分为三大类[6]：1)基于统计决策的方法，主要有层次分析法、模糊综合评判法、加权法、证据理论评估法；2)基于数据挖掘的方法，主要有关联规则法、聚类分析法等；3)基于机器学习的方法，主要包括支持向量机法、贝叶斯网络法和人工神经网络法。由于雷达系统结构复杂、技术密集，对其质量评估不仅要考虑装备本身，还要兼顾雷达的履历数据、环境应力信息、操作应用能力等因素。其中部分因素无法通过数据直观体现，仅靠数据驱动的评估方法难以满足指标需求，需要依据专家的经验知识进一步评判[7-8]。因此，本文对雷达系统进行评估时，采用模糊综合评判的方法，将定性分析和定量计算相结合，以满足各个指标的评估需求。针对测试数据，通过组合隶属度函数获取评价信息，对不能用数据直接表示的指标，则采用专家打分的方法，兼顾考虑了指标因素的主观性和客观性。

1 模糊综合评判相关理论

1.1 模糊综合评判模型

模糊综合评判是综合考虑各种影响因子，运用模糊数学理论对被评对象给出综合评价的一种方法。该方法能够对被评对象按照综合评分的高低进行排序和评价，还可依照最大隶属度原则，对照模糊评价集上的值判定对象所属的评估等级。

模糊综合评价实施步骤[9]：

1)首先确定需要评价的指标因素集合U={U1,U2,…,Un}。

2)确定评语集合V={V1,V2,…,Vm}；无论被评价的指标有多少个层次，评语集只有一个。式中的m表示评语等级的个数，一般情况下取4～9，常用的是4级或5级。

3)建立模糊评判矩阵：对因素集中每个因素Ui进行单因素评判，Ui在评语集中Vj的隶属度为rij，由此建立模糊评判矩阵R。

4)确定权重集：由于不同的评价因素其重要程度有所不同，所以对各因素分配不同的权重，以体现重要度的差别。如因素Ui的权值为wi，所有因素的权重集为W={w1，w2，…，wi}。

5)模糊评判计算：建立模糊评判计算模型B=W∘R,其中“∘”表示模糊综合算子。为避免主观性，本文对雷达质量评估分析不会对某个指标存在偏好，所以选取加权平均型的模糊综合算子(∘+，)，该型算子能够依据指标权重的大小充分考虑指标的所有信息。

6)对评价结果进行分析：针对模糊综合计算所得结果进行分析评价，以此确定评判等级。对模糊结果向量常用的分析方法有模糊向量单值化法、最大隶属度原则等[10]。

1.2 隶属度

1965年，美国自动控制专家L.A.Zadeh教授提出了隶属度的概念，用以定量描述模糊性对象。隶属度通过隶属函数表现出来，在模糊评判过程中，起着关联评价元素与评价等级的作用，正确选取或构造隶属函数是影响综合评判效果的关键[11]。传统的模糊综合评判采用一种隶属度函数进行评估，这就要求隶属度函数尽可能符合所评对象的应用实际，对函数的选择要求比较高。在工程应用中，因评价标准划分的不同或监测数据的异常，有时可能会发生隶属度突变的情况，影响整体评价效果[12]。为解决这一不足，本文选用组合隶属函数进行隶属度的改进计算，尽量使各指标隶属函数合理可信，消除隶属度突变的不利影响。

确定隶属度的常用方法有3种：专家打分法、模糊统计法、模糊分布法。专家打分是由专家根据一些准则或经验对评价对象某些指标进行打分确定；模糊统计法是通过拟合原始数据的连续分布函数，来推算表达结果[13]；模糊分布表达的是实数域R上模糊集合的隶属函数。区分不同的应用研究，应选择不同的隶属函数。由于雷达系统的底层参数不符合连续分布，因此模糊统计法并不适用，本文选取模糊分布和专家打分的方法相结合，依据雷达应用实际确定模糊分布参数。

1.3 组合隶属函数的构建

模糊隶属度函数分为3种类型，即偏小型、偏大型、中间型。其分布形式主要有三角形、梯形、抛物线型、柯西分布、岭形分布和正态分布等[14]。在评估过程中,选择不同类型的隶属度函数其评价结果也会有所差异。与单一隶属度函数相比，组合隶属函数的优点是对多个隶属函数的信息优化组合，充分利用多种评价信息，消除单一隶属函数可能发生异常突变的不利影响，使所求的隶属度可信性更高[15]。在许多应用中也验证了组合评估模型可以有效减小波动,提高评估值的稳定性和可信度。

组合隶属函数的构造步骤如下[16-17]：

1)根据选定的评估要素、评价等级，以及参数特性选择合适的隶属度函数。

2)计算单一评价要素在不同隶属函数条件下的隶属度，而后求出该要素的隶属度均值：

(1)

式中的ri是指某单个要素在第i个隶属函数下算出的隶属度值;n指的是共有n种隶属度函数。

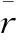
关于w1对于Var(ec)求极小值，得：

(2)

因w2=1-w1，令方差Var(e1)=σ11，Var(e2)=σ22，协方差cov(e1,e2)=σ12，由e1,e2相互独立，则协方差cov(e1,e2)=σ12=0，则有：

(3)

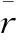
(4)

其中:i=1,2,…，n。由此可见，σii越小，隶属函数求出的隶属度越接近平均值，所得的权重就越大。明显可知，若r1,r2，…，rn都为零，则wi相同。根据以上步骤可以计算出每个隶属函数的权重，因此构造最终的组合隶属函数为：

rc=w1r1+w2r2+…wnrn

(5)

新的隶属函数对各隶属函数进行了优化组合，突出了实用性较好的函数的作用，又兼顾了实用性一般的函数信息，从而使最终的评判结果可信度更高。

2 雷达装备质量评估模型

2.1 雷达质量评估步骤

根据以上理论，可以构造某雷达系统的质量评估模型，其基本实施步骤为：

第一步，依据雷达功能特性进行评估指标分析，收集获取监测数据、履历数据和环境数据等评价因素，分类确定底层指标，区分目标层和指标层，建立评估体系。

第二步，确定评语集，即为雷达系统划分质量评价等级，根据雷达装备实际，一般划分“较差、一般、良好、优秀”4个质量等级。

第三步，根据已经确定的底层指标元素，区分定性指标和定量指标分别计算隶属度。对于能够通过测试所得的指标数据，选取合适类型的隶属函数计算各自对应的隶属度。本文选择3种类型的隶属函数分别对底层元素指标进行隶属度计算，而后运用方差-协方差法求解各指标的组合隶属度。对于不能用数据表述的定性指标，则采用专家打分的方法确定指标的隶属度。

第四步，基于确定的评价指标和构建的评估体系，由下而上分层构造模糊评判矩阵，并对矩阵进行归一化处理获得标准化矩阵。运用熵权法，对标准化矩阵内的指标元素逐层计算其熵值和权重。

第五步，基于求出的各层次指标权重和各底层指标因素的隶属度，进行模糊综合评判计算，求得评价结果，确定雷达系统的质量等级。

其中，各指标的熵权、隶属度和最终模糊综合评判的计算均借助Matlab软件程序来实现。

2.2 熵权法基本理论

熵(Entropy)最初是由热力学研究中提出的一个物理量，用以刻画分子状态在某一系统中的出现程度。应用于信息论后，熵主要用来表征系统的无序程度，能够反映每个指标在一个系统或样本中所占信息量的多少[18]。熵权法就是从信号系统科学发展出来的一种权重计算方法，该方法能将评价指标包含的信息进行综合量化与赋权，具有一定的客观性，可以有效减轻评估过程中主观因素对评价结果的影响，在工程实践领域有广泛应用。

在装备质量的评价分析中，各评判指标重要程度不同，可以用熵的概念反映各指标因素所占的权重比例，即某一指标因素的信息熵越大，说明该指标变异度越小，在评价中包含的信息量小，其所占的权重比例越小。反之，指标的信息熵越小，变异程度越大，反映的信息量大，其权重值也越大[19]。

熵权法确定指标权重具体步骤如下[20]：

1)建立标准化样本矩阵：

设一个样本空间中有m个评价要素，n个评价指标，形成样本的判断矩阵R=[rij]m×n，将该矩阵进行归一化处理，得到样本标准化矩阵Z=[zij]m×n，其中，rij和zij分别为原判断矩阵和标准化后矩阵中的元素。

2)计算每组样本中单个指标所占的比例：

其中:aij表示第j个指标下，第i个元素的占比。

3)计算每个评价指标的熵值：

4)确定指标的熵权：

通过以上步骤计算，可得到所有指标的权重向量W，记为矩阵W=(wj)1 ×n。

2.3 雷达装备评价指标体系及权重

通过调查研究发现，传统的雷达质量评定和等级划分方法，过多依赖贮存年限和维修次数等装备的设计数据、履历数据等因素，而对其他指标的描述过于主观，尤其对装备实际的测试数据利用不足，存在一定的片面性。本文在兼顾雷达设计履历和环境因素的基础上，综合考虑雷达的整机性能指标和工作状态参数等监测数据，从较为全面的角度对其质量状态进行评价。经充分征求专家意见，结合应用实际，区分目标层和指标层，将某雷达底层参数合理归类，构建雷达系统的三级评价指标体系，如图1所示。其中，监测数据指标分为整机性能指标(包括发射机功率、噪声系数、幅相一致性、幅频特性、改善因子、天线增益、驻波系数、暂态特性、跟踪性能)和工作状态数据(包括P显扫描线长度、发射机紧急开机时间、发射机高压、脉冲宽度、接收机场放电流、接收机本振检测电平、天线转速和电源电压)。履历数据分为齐套性指标(包括装备完好率、备品附件齐全率)、可靠性指标(包括等效服役时间、平均故障时间、机械性能)、维修性指标(包括维修保养情况、关重部件磨损情况、锈蚀老化情况)。环境数据分为地域环境(包括气候地区、海拔高度、电磁环境)和天气环境(包括雨雪、盐雾、沙尘、温度、湿度)。

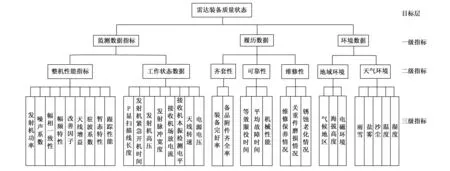
图1 某型雷达质量评估指标体系结构

根据上述指标体系结构，运用熵权法的计算步骤，采用Matlab软件进行运算，得到雷达系统各级指标因素的权重划分，具体如表1所示。

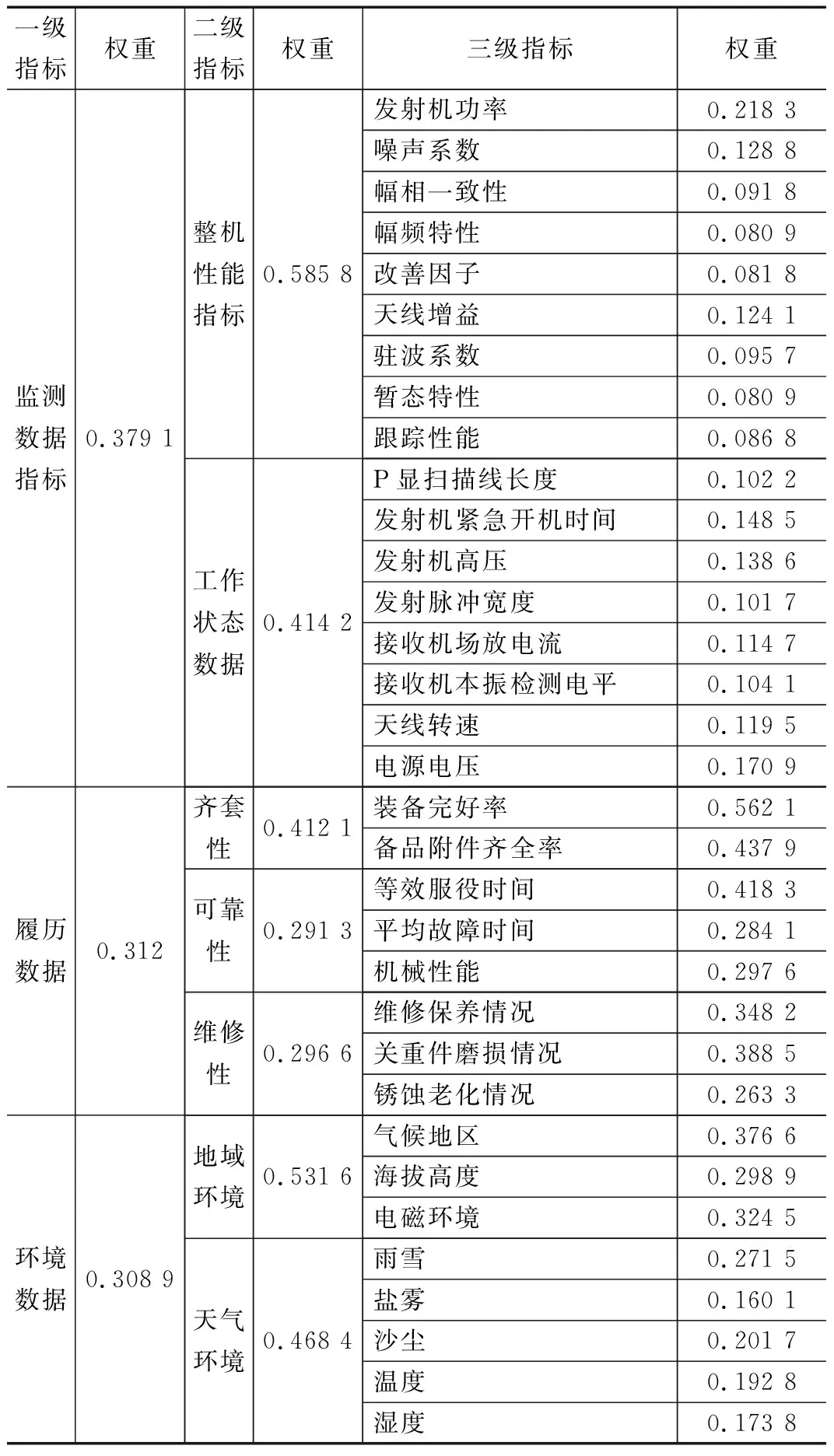
表1 某型雷达系统各级评估指标权重

3 模糊综合评判计算

依照模糊评判流程，在确定评价指标因素后，需要确定评价准则，评价准则因评价目标不同也有所区别。通常依据系统的评价目标和参数的属性确定评价准则。结合雷达工作效能，本文建立4个等级的评估标准：1)优秀：0.8～1；2)良好：0.6～0.8；3)一般：0.4～0.6；4)较差：0～0.4。确定了各指标权重和隶属度后，采用加权求和算子(∘+，)进行模糊计算。

3.1 某型雷达底层指标边界值及测试值

模糊综合评判的方法是由下至上逐层进行评估计算，上层的隶属函数由其下层计算而来[21]。因此，掌握最底层指标的属性及边界值是评估运算的基础。本文以某型雷达为研究对象，根据其具体指标参数的取值范围，并加以实际测量，列出其底层评估指标的边界值及测试值，部分数据如表2所示。

表2 某型雷达装备底层指标边界值及测试值

3.2 基于组合隶属函数的模糊综合评价

根据雷达系统涉及的评价因素、评判等级和指标数据特性，选择中间型的隶属函数计算隶属度，能提高指标数据的普适性。Trapmf(梯形)、Dsigmf(双S形)和Pimf(π形)这3种类型的隶属函数都是中间型的函数，且在区间分布上图形结构相似，符合模糊数学的特性。因此本文选择上述3种隶属度函数分别进行计算，依照表2中雷达底层指标的边界值和测试值，求得各指标关于评语集的隶属度函数，再利用方差-协方差优选法构造组合隶属函数，从而计算出各指标的最终隶属度。通过Matlab程序运算，得到如表3所示的各指标具体隶属度值。针对优秀、良好、一般、较差4个评级标准，图2～5分别给出了梯形、双S形、π形以及组合后的隶属函数曲线。经组合改进的隶属度函数，可信度更高，能够简化对数据的要求，提高评估的可靠性。

表3 某型雷达底层指标隶属度关系

图2 较差等级隶属度对比曲线

图3 一般等级隶属度对比曲线

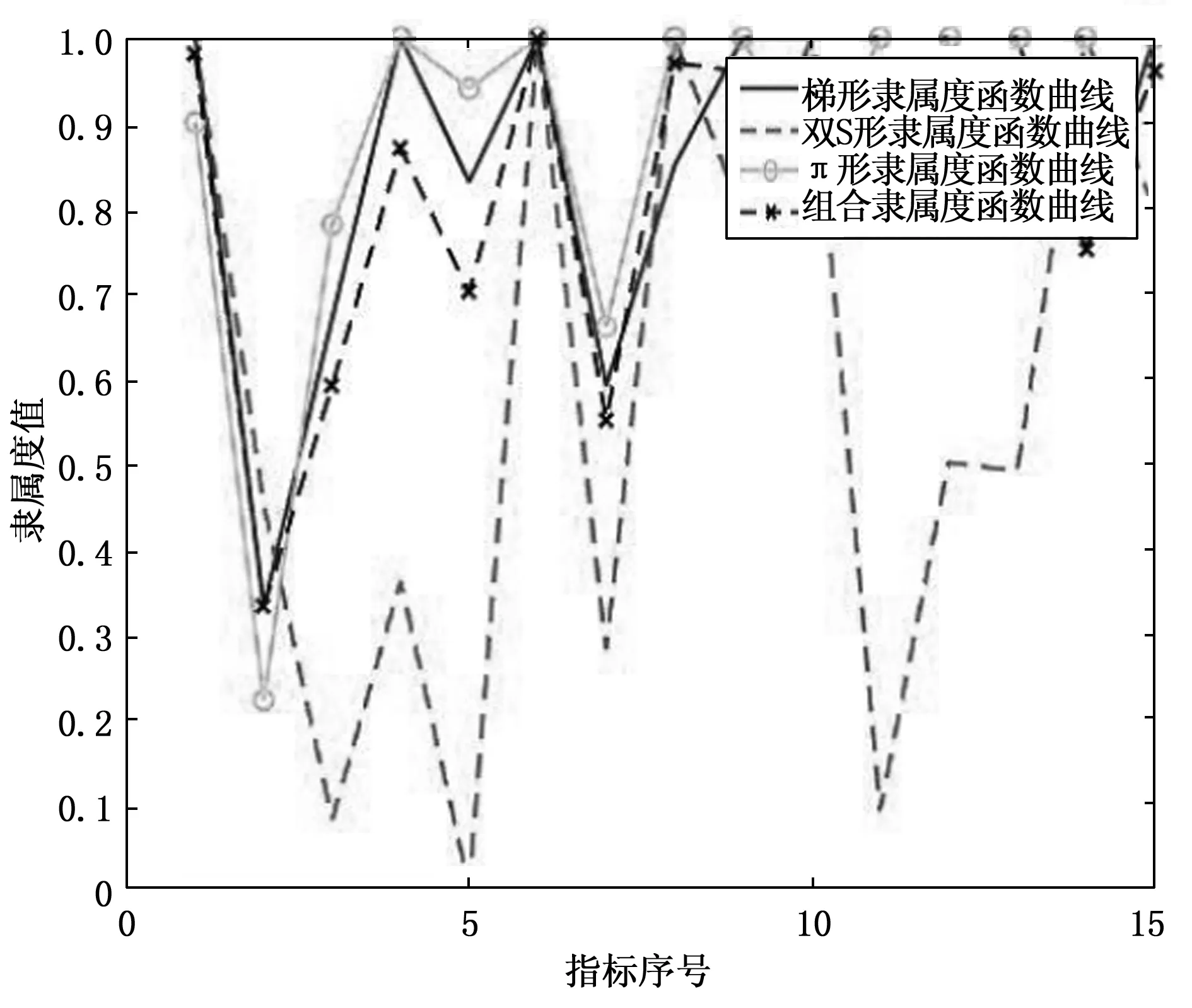
图4 良好等级隶属度对比曲线

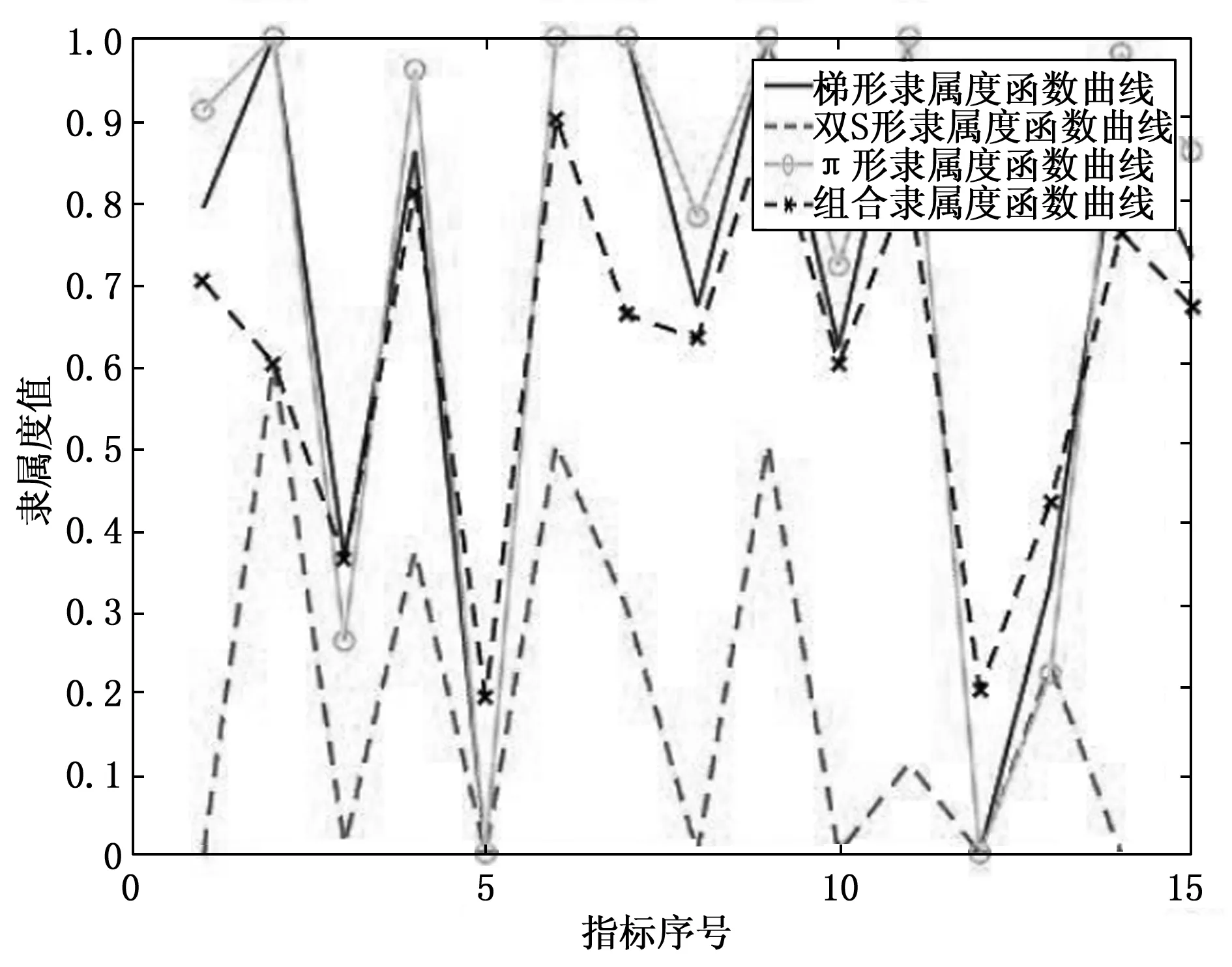
图5 优秀等级隶属度对比曲线

对无法直接测量的指标参数，其隶属度采用专家打分的方式给出。某型雷达指标的专家打分隶属度关系见表4，由此确定了雷达系统所有定性指标和定量指标的隶属度。求得各指标的权重和隶属度后，采用加权求和算子(∘+，)进行模糊计算。按照整机性能指标、工作状态数据、齐套性、可靠性、维修性、地域环境、天气环境7个方面构造一级评判矩阵。以可靠性指标为例，对其进行一级模糊评判计算：

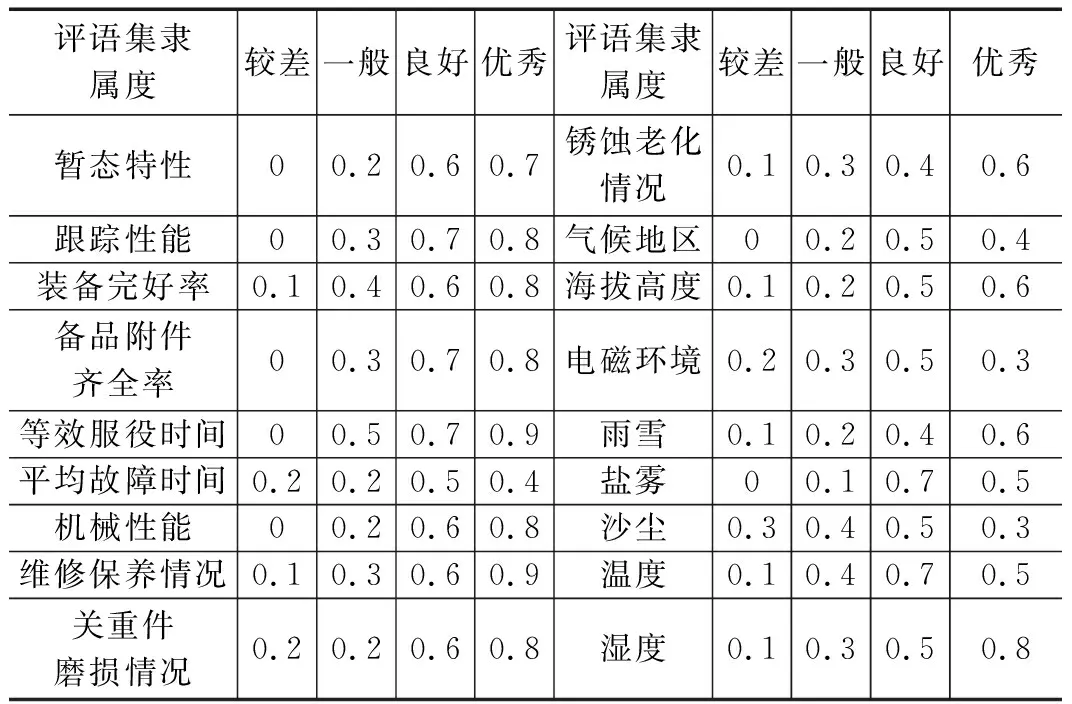
表4 某型雷达指标专家打分隶属度关系表

B1=W1∘R1=

(0.0568,0.3255,0.6134,0.7282)

同理，可以求得其他一级评判矩阵的评价结果。

依此采用自下而上多级模糊综合评判的方法，逐层运算，得到最终的评价结果向量：A=(0.0975 0.3486 0.6482 0.6321)，依据最大隶属度原则，该型雷达的质量等级为良好。

4 结束语

本文以某型雷达为研究对象，建立了雷达系统的评估指标体系和评价模型，采用熵权法确定评价指标权重，采用组合隶属函数的方法计算底层指标隶属度，有效避免了单一隶属度函数可能产生的隶属度突变问题。利用模糊综合评价计算评估结果，较好地将专家知识的主观性与监测数值的客观性相结合，较为全面地对雷达系统质量进行了评价。通过对某型雷达评价实例分析，其评判结果符合预期，验证了该评估方法的有效性，对雷达维修保障有一定的参考价值。