基于FPGA的深度强化学习硬件加速技术研究
2022-07-09王宾涛李喜鹏
凤 雷,王宾涛,刘 冰,李喜鹏
(哈尔滨工业大学 电子与信息工程学院,哈尔滨 150001)
0 引言
强化学习(RL,reinforcement learning)是指从环境状态到动作映射的学习,以使动作从环境中获得累计奖赏值最大[1],经常被用于序贯决策层问题。与监督学习[2]不同,RL算法主要强调智能体与环境的交互,在二者的交互的过程中,环境会根据智能体所处的状态以及所决策的动作给予其一定的奖惩信号,智能体则会根据所获得的奖惩信号对自身的决策策略进行优化,从而最大化决策过程中所获得的累计奖励。
2013年,DeepMind团队将深度学习中的卷积神经网络(CNN,convolutional neural network)[3]算法与传统强化学习Q学习[4]相结合,设计了DQN算法[5],在雅达利游戏平台中取得了比人类玩家更高的游戏分数,从此掀起了一股深度强化学习[6]的研究浪潮。后续DeepMind团队基于DRL算法所研发的AlphaGo[7]和AlphaGo Zero[8]在机器博弈领域取得了巨大成功,更是成为了人工智能领域的里程碑事件。目前,DRL除了在游戏中进行应用外,直接在边缘设备上实现DRL同样有巨大的应用价值和广泛的应用前景,例如为充当巡逻机器人的无人机 (UAV, unmanned aerial vehicle)[9]提供自主避障和航路规划的能力,为无人车辆[10-11]提供自主驾驶分析决策能力。
DQN算法作为DRL领域的开山之作,被后续许多的DRL算法所借鉴。其解决了传统Q学习的“维度灾难”问题,采用多层神经网络来完成值函数的非线性逼近功能,替代传统的Q表查询决策方式,将神经网络的感知能力和强化学习的决策能力结合,实现端到端的感知与决策。在智能体与环境交互的过程中,同时存在神经网络的推理与训练两类运算,这两类运算都具备计算密集型的特点,需要较强的算力才能保证算法的实时性。
DQN计算密集型的特点,对于计算资源和功耗都受限的边缘设备而言,直接实现深度强化学习算法存在一定的挑战。这种挑战主要来自于两方面:一方面是DQN算法本身计算密集型特点和计算数据之间较强的依赖关系;另一方面是大多数嵌入式计算平台本身单指令单数据流计算架构的局限性,无法支持面向DQN的高性能计算。这导致有关在嵌入式设备部署DQN算法的研究进展十分缓慢,相关研究现状在1.2节中得到阐述。面向边缘在线决策应用,本文提出一种基于FPGA平台的DQN算法实现方法,可以在FPGA平台上完成DQN算法的推理和训练。主要工作如下:
1)提出了一种基于FPGA平台的DQN算法的硬件实现架构,架构中的加速器IP核采用流式架构设计,可以灵活配置算法的训练超参数。
2)在FPGA平台计算资源和存储资源的约束下,提出了一种设计空间的探索方法。通过定量分析DQN算法实现所需的存储资源和计算资源,获得DQN算法在FPGA中进行加速部署时每一层的并行计算参数。
3)面向典型应用Cartpole搭建了应用验证平台, 在FPGA平台上进行了设计的功能验证和性能测试,并在网络的训练时间和功耗方面同CPU平台和GPU平台进行了实验对比。
1 背景
1.1 DQN算法
RL的基本模型可以用图1表示,通过智能体与环境的信息交互,实现决策功能。整个过程可用四元组

图1 强化学习基本模型
Q学习算法[4]作为一种经典的RL算法,使用Q查询表存储各个动作对应的Q值,通过查询每个动作的Q值,指导智能体做出相应决策。受限于计算机存储的限制,Q表在处理高维状态数据方面表现不佳[12]。

(1)
1.2 FPGA加速强化学习算法
近年来,机器学习在嵌入式边缘设备上的加速实现[14],已经成为人工智能领域[15]的热门话题,FPGA由于其低功耗、高能效和可重构的特点,在硬件加速领域[16]备受青睐,目前最先进的机器学习加速器大多支持监督学习,如CNN[17]、循环神经网路(RNN,recurrent neural network)[18]等,但对深度强化学习的硬件加速目前还处于刚刚兴起的状态。
Shengjia S等人在Stratix系列FPGA上对TPRO算法(TRPO, trust region policy optimization)进行了硬件加速以应用于机器人控制应用[19],后续提出了一种设计空间探索方法对TRPO 算法加速进行进一步的优化[20]。S.Jiang等人采用单引擎架构,在Altera Arria 10上实现了Deep Q-Learing算法的硬件加速[21]。但是上述研究,在计算架构和设计空间探索等方面仍有很大提升空间。
2 基于DQN的FPGA硬件架构和加速器设计
2.1 总体硬件架构
如图2所示,总体硬件架构主要包括外部存储器(DDR, direct digital radiography)、处理单元(PS,processing system)、可编程逻辑部分(PL, processing logic)的加速器和片内外总线互联。我们通过PS和PL协同工作来高效的完成DQN算法的计算,其中PS部分主要负责与环境进行交互,奖励函数的计算,DDR中训练经验池的维护,以及对PL进行超参数和工作模式的配置;PL部分定制化设计DQN算法加速器,用于实现算法中神经网络的前向推理、误差反向传播和权值更新等计算密集部分,PL部分加速器结构设计、加速算子设计及相关设计空间探索方法是研究的核心。

图2 总体硬件架构
2.2 加速器结构设计
整个加速器采用流式架构,针对DQN算法的各个模块进行硬件定制化设计。DQN算法加速器IP核的结构如图3所示,定制化设计了Target_Q模块、Current_Q模块、损失函数计算模块、权值更新和替换模块、控制模块和参数存储单元。其中Target_Q模块用于完成Target_Q网络的前向推理;Current_Q模块用于完成Current_Q网络的前向推理和反向传播;控制模块用于对加速器的工作模式和训练参数进配置,使得各个模块能够协同工作;权值更新与替换模块用于实现Current_Q网络的权值更新和Target_Q网络的权值替换;损失计算模块主要用于实现损失函数的计算。

图3 DQN加速器结构图
加速器存在两种工作模式:一种是直接利用学习好的权值参数,与环境交互后,智能体只做出决策但不进行学习;另一种是做出决策后智能体会根据环境给予的奖励反馈进行学习,调整自身权重参数。
Target_Q模块和Current_Q模块是整个硬件加速过程中的设计重点,在本设计中,Target_Q模块和Current_Q模块均由加速算子(VMPU, vector matrix processing unit)通过流式先入先出寄存器(FIFO, first in first out)级联组成,加速算子的具体细节将会在2.3节中介绍,同时将在2.4节介绍本设计的设计空间探索方法。
2.3 加速算子VMPU设计
DQN算法中的神经网络选择多层感知机,针对多层感知机中向量矩阵乘法计算密集型的特点,以及前向推理和反向传播计算过程间的数据依赖,基于FPGA硬件资源的特点,设计了单指令多数据(SIMD, single instruction multiple data)运算和多处理单元(PE,processing element)两种加速模式,其设计示意图如图4所示。SIMD主要用于完成CNN中的层累加单元,即通过在FPGA内部定制化设计SIMD,通过硬件实现基础的层累加模块,完成基于指令集的硬件加速;PE主要用于实现多个SIMD的并行计算;在单个PE内实SIMD并行的同时,VMPU单元内还实现了多个PE的并行计算,以达到最大化硬件加速性能的目的。
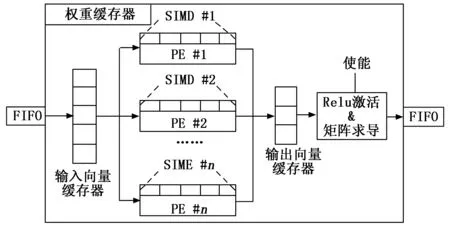
图4 VMPU设计示意图
VMPU的输入是上一个计算单元的输出或者最原始的输入,经过FIFO寄存器被存储在VMPU内置输入向量寄存器,用于神经网络卷积计算的权重已经部署到FPGA内部,此使输入向量寄存器的元素与已经部署好的权重展开并行计算,并将结果放到输出向量寄存器内,进而经过激活、矩阵求导等操作后,作为输出被传送到下一计算单元。
在FPGA实现VMPU的过程中,前向推理与反向训练的计算过程之间存在相关度较高的依赖关系,为了解决DQN中层间推理与训练的数据依赖关系,同时实现FPGA并行计算,需要在FPGA片上对权重矩阵进行分区存储,基于计算过程中权值矩阵维度设计了两类VMPU,分别是以列为主的VMPU(A)和以行为主的VMPU(B),两类VMPU的存储方式划分示意如图5所示。在VMPU(A)中,SIMD并行对应矩阵的行维度,PE并行对应矩阵的列维度;由于两类VMPU的权重矩阵存储方式互为转置,在VMPU(B)中,并行计算对应的维度与A模式相反。在部署DQN网络时,对于奇数层而言,前向推理时使用VMPU(A),反向传播时使用VMPU(B);对于偶数层而言,前向推理时采用VMPU(B),反向传播时采用VMPU(A)。

图5 片上权值存储方式
如图6所示,以VMPU(A)为例,具体说明矩阵加速算子的计算过程。假设网络第一层的神经元个数为8,第二层的神经元个数为4,在进行前向推理时,相当于执行一个1*8的向量与8*4的矩阵的乘法。在VMPU(A)中,如图6(a)所示,假定SIMD取4,PE取2,则行维度的折叠因子SF为2,则列维度的折叠因子PF为2,折叠因子的计算方式将在2.4节阐述。由SF和PF可算得总折叠因子为4,即循环4次便可完成整个向量矩阵乘法的计算。在第一次循环中,如图6(b)所示,首先计算输入向量前4个元素a1-a4与权值矩阵对应元素的乘积累加,生成c1和c2的中间结果,第二个循环继续计算权值矩阵当前列未进行计算的元素,生成的乘积累加结果与之前的中间结果相加,生成c1和c2的最终结果,然后加上偏置,进行激活函数的计算。同时,激活函数的梯度也将在此时计算,并存储在片上以供反向传播使用。最后,将两个最终计算结果c1和c2流入FIFO中。

图6 VMPU(A)计算示意图
VMPU(A)将两个最终结果流入FIFO后,后续连接的VMPU(B)将在此刻收到启动信号,从FIFO中取出上一层的输出数据,存入输入寄存器中,开始第二层的计算。与VMPU(A)类似,VMPU(B)的内部同样为乘累加树结构,但其计算逻辑是以行为主,每完成一次循环,生成的都是中间结果,直到最后一次循环结束,VMPU(B)将会累加出最终的计算结果。通过选取合适的并行参数,便能让级联的VMPU(A)和VMPU(B)之间形成流水,只要VMPU(A)的计算不中断,每隔一段时间,VMPU(B)便会接收来自VMPU(A)的数据并进行下一层的计算,两层之间形成数据流水后,两层整体的计算时间大概等于VMPU(A)的计算时间。
2.4 设计空间探索
为了满足DQN算法特性和FPGA硬件平台资源约束,确定网络部署的并行计算参数,对设计空间探索方法进行研究是十分必要的。不同于研究[21]中仅考虑了DSP资源,本设计在建立资源模型的同时考虑了DSP资源和BRAM资源,达到对计算资源和存储资源设计空间探索的目的。
Target Q模块和Current Q模块的计算过程最为耗时,对于以上两个模块,其内部的VMPU单元采用A-B-A-B的方式级联而成,通过对总循环次数FoldCycle进行建模,完成设计空间探索问题中性能模型的寻优,此处FoldCycle可用于表征VMPU模块的计算时间。如公式(2)所示,设计空间探索问题,在软硬件资源约束的情况下,寻求最小的总循环展开次数。本文首先将先对VMPU单元的A模式和B模式分别进行建模,然后再对整个系统进行建模。

(2)
式(2)中,FoldCycle代表总循环展开次数;P代表循环展开参数的集合,该集合可用VMPU中的循环展开参数PE和SIMD表示;LayerSizei代表神经网络第i层的大小;DSPtotal、BRAMtotal代表设计实际消耗的总的计算资源和存储资源个数;DSPFPGA_Limit、BRAMFPGA_Limit代表FPGA平台的计算资源和存储资源的限制。
首先对VMPU(A)进行分析,在向量矩阵乘法中,使用RowSize表示权重矩阵的行维度大小,SIMDA为VMPU(A)的行循环展开参数,sfA为其对应的行并行折叠因子;使用ColSize表示权重矩阵的列维度大小,PEA为VMPU(A)的列循环展开参数,pfA为其对应的列并行折叠因子;则VMPU(A)的总循环展开因子FoldCycleA为sfA和pfA的乘积,相关计算关系可用公式(3)~(5)表示:
sfA=RowSize/SIMDA
(3)
pfA=ColSize/PEA
(4)
FoldCycleA=sfA*pfA
(5)
然后对VMPU(B)进行分析,在向量矩阵乘法中,同样使用RowSize表示权重矩阵的行维度大小,PEB为VMPU(B)的行循环展开参数,pfB为其对应的行并行折叠因子;使用ColSize表示权重矩阵的列维度大小,SIMDB为VMPU(B)的列循环展开参数,sfB为其对应的列并行折叠因子;则VMPU(B)的总循环展开因子FoldCycleB为pfB和sfB的乘积,相关计算关系可用公式(6)~(8)表示:
pfB=RowSize/PEB
(6)
sfB=ColSize/SIMDB
(7)
FoldCycleA=pfA*sfA
(8)
采用A-B级联模式,可以实现层间的流水计算与并行计算,进而增加硬件加速的性能。为了实现A-B级联模式,级联的两层应当满足公式(9)的要求,这样可以解决VMPU(B)对VMPU(A)的数据依赖。当VMPU(A)与VMPU(B)之间形成层间的计算流水后,A模式的计算时间便能掩盖B模式的计算时间,如公式(10)所示,式(11)中FoldCycleAB表示级联的两层计算所需的循环数。
sfA≥sfB
(9)
FoldCycleAB=FoldCycleA
(10)
在本设计中,我们实现了3个层次的流水以及并行设计,第一个是VMPU内部的乘积累加流水以及多个乘累加树的并行;第二个是VMPU通过A-B级联时,形成层与层之间的计算流水;第三个是在训练时,Target_Q模块与Current_Q模块之间形成并行计算,Target_Q模块的计算时间将被Current_Q模块的计算时间掩盖。因此,整个系统的时间消耗主要由Current_Q模块决定。系统处理决策样本所用的循环数如公式(11)所示,式中FoldCycleFP表示前向推理在Current_Q模块所消耗的时间,FoldCycleBP表示反向传播在Current_Q模块所消耗的时间。
FoldCycle=FoldCycleFP+FoldCycleBP
(11)
除运行时间参数进行建模外,设计还对DSP计算资源和BRAM存储资源进行建模。VMPU中DSP资源的消耗量与流水计算的启动间隔(II,initiation interval)有关,当II为1时,消耗的DSP资源最多,当II大于1时,VMPU将对DSP资源进行复用,所消耗的DSP资源如式(12)和(13)所示,式中常系数5表示浮点型层累加单元所消耗的最小DSP个数。设计采用了FPGA空间换取时间的并行加速思想,存储单元采用BRAM实现,其使用数量和加速结构有关。算子并行度为SIMD*PE,则需要2*SIMD*PE个BRAM单元来存储输入向量和权重,同时需要PE个BRAM来存储偏置变量。故对于VMPU中BRAM资源的消耗可用公式(14)和(15)表示:
DSPA=ceil((SIMDA/IIA)*PEA)*5
(12)
DSPB=ceil((SIMDB/IIB)*PEB)*5
(13)
BRAMA=(SIMDA*PEA+PEA)*2
(14)
BRAMB=(SIMDB*PEB+PEB)*2
(15)
本设计中消耗BRAM资源和DSP资源的主要模块为Target_Q模块、Current_Q模块和权值更新与替换模块,因此,可以按照公式(16)估计系统相关资源消耗的总体情况。
BRAM=Target_QBRAM+Current_QBRAM+UpdateBRAM
DSP=Target_QDSP+Current_QDSP+UpdateDSP
(16)
3 实验评估
3.1 应用介绍
使用OPEN AI Gym提供的Cartpole环境对设计进行测试,Cartpole游戏环境如图7所示。 CartPole是一个非常经典的车杆游戏,游戏里面有一个小车,车上有竖着一根可以旋转的杆子,每回合中车杆的初始状态都会有所不同,小车需要左右移动来保持杆子竖直。为了保证游戏继续进行,需要满足以下两个条件:
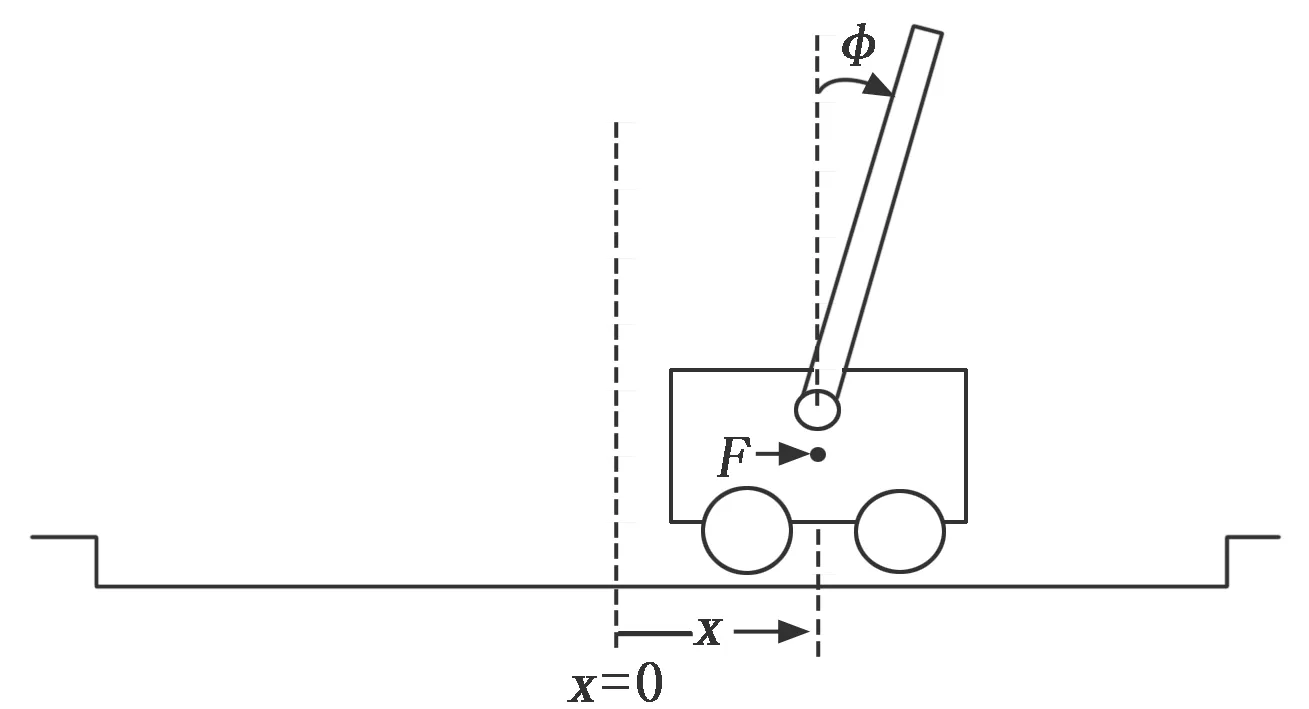
图7 Cartpole应用
1)杆子倾斜的角度φ不能大于15°.
2)小车移动的位置x需保持在一定范围内(±2.4个单位长度)。
3.2 实验过程与参数设置
本文所搭建的应用验证平台如图8所示,用于对设计进行功能验证和性能分析。应用验证平台分为两个部分,分别是PC机和ZYNQ7100平台。我们在ZYNQ的ARM端搭建了Linux操作系统并编写了Cartpole应用程序,在PC机上运行gym中的Cartpole环境,边缘侧的ZYNQ与PC机中的环境通过网口进行通信,以模拟智能体与环境的交互过程。训练开始后,ZYNQ将会向PC机中的环境传递动作信息,环境收到信息会后向ZYNQ反馈执行动作后的奖励、下一刻的状态信息和当前回合是否结束的标志。

图8 Cartpole应用验证平台
我们使用含有一个隐藏层的多层感知机作为DQN算法的基础网络,来进行Cartpole游戏的控制,网络的结构为4-320-2。针对三层的感知机网络,可以使用4个VMPU进行A-B级联完成Current_Q模块的搭建,使用2个VMPU完成Target_Q模块的搭建。根据本文所提的设计空间探索方法,对Cartpole应用中DQN网络在ZYNQ 7100上的部署实现进行寻优,求得各个单元的循环展开参数大小:SIMDA=4,PEA=PEB=32,SIMDB=2。
3.3 实验结果与分析
FPGA中加速器部分的设计使用赛灵思公司的Vivado HLS(v2018.3)开发工具,表1为Cartpole应用加速器的资源使用情况,从表中可以看出,通过设计空间探索预估的BRAM和DSP资源与实际消耗的相差无几,稍微的误差存在于预估过程未加入损失计算单元消耗的相关资源。通过对资源利用率的观察,证明了所提出的设计空间探索方法的高效性。

表1 资源使用报告
为了探究本文FPGA加速器的对DQN算法的整体加速性能,进行了与CPU、GPU的对比实验,相关硬件平台的型号、频率如表2所示。时间测量采用时间戳计数的方式;GPU和CPU的功耗采用各自额定功率表示,加速器的的运行功耗使用Vivado软件综合预估的额定功率表示;相比于FPGA的运行时间,计算3种平台的加速比,相关实验结果如表2所示。
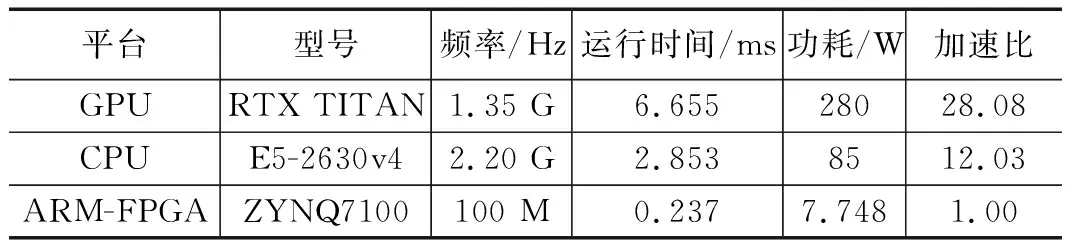
表2 3种硬件平台训练32个样本处理时间对比
从表2可以看出,与GPU、CPU对比,本文提出的FPGA加速器运行速度提高了28.08和12.03倍;基于FPGA设计的加速器在运行功耗方面也具有明显的优势。
4 结束语
本文提出了一种用于DQN算法加速的硬件架构及其设计空间探索方法,其采用流式结构实现加速器IP核设计。通过设计空间探索,我们可以针对不同和DQN网络和芯片平台进行硬件加速实现。以Cartpole应用为例,我们设计了一个三层的DQN网络,通过设计空间探索寻得了全局最优的并行计算参数,然后在ZYNQ 7100平台上完成了设计的部署测试,测试结果表明,FPGA在训练时的计算时间和功耗方面相对于GPU/CPU具有明显的优势。
