基于SSVEP的空间机械臂脑机交互方法

钱一润，王从庆，张闻锐，展文豪，张 民

(1. 南京航空航天大学 自动化学院，南京 210016; 2. 中国航天员科研训练中心 人因工程国防科技重点实验室，北京 100094)

0 引言

空间机械臂是空间站中用来完成目标搬运、在轨建设和辅助航天员出舱等任务的智能设备，具有强大的应用能力和广阔的发展前景。空间机械臂可以由航天员遥控进行操作，然而在失重的环境影响下，航天员很难像在地面一样自如地操控空间机械臂。脑机接口(BCI，brain-computer interface)作为一种可以直接实现大脑与外界间信息传输的通道[1]，可以通过脑机接口技术对大脑中的神经信号进行解码并传输给空间机械臂，实现航天员与空间机械臂之间的脑机交互控制。稳态视觉诱发电位(SSVEP，steady-state visual evoked potential)是一种受持续视觉刺激而产生的脑电信号[2]，根据其原理而设计的SSVEP脑机接口凭借着频域特征明显、可选择的目标数多、信息传输速率快且受试者不需要经过训练等优势，在对信息传输要求较高的场合已被广泛使用。

传统的SSVEP信号分析方法主要有功率谱密度分析[3](PSDA，power spectral density analysis)和典型相关分析(CCA， canonical correlation analysis)等。功率谱密度分析是一种单通道分析方法，通过将脑电信号从时域转换到频域[4]，比较信号的频率成分和相对强弱来对受试者关注的视觉刺激进行分类。作为目前主流的SSVEP分类方法，典型相关分析及其改进方法被广泛应用，CCA方法可以计算出两组多维变量之间的相关性[5]。Lin等人[6]提出的CCA方法通过分析脑电信号与模板信号之间的相关关系来对SSVEP信号进行分类。作为一种多通道方法，CCA具有高效性和鲁棒性，已成为一种SSVEP信号分类的经典方法。陈小刚等人[7]在CCA的基础上有效地利用了信号中的谐波成分，提出了改进方法滤波器组典型相关分析(FBCCA，filterbank canonical correlation analysis)，进一步提高了信号的分类准确率。近年来，深度学习已经在很多领域成为了一种热门方法。引入深度学习来对SSVEP信号进行分类，相比于传统方法，深度学习在学习数据特征方面有着天然的优势，卷积神经网络[8](CNN，convolutional neural network)是最常使用的算法之一。杜光景等人[9]使用了一个7层的CNN网络对原始的多通道SSVEP信号进行分类，在针对短时间的SSVEP信号时，有效地提高了信号的分类准确率和鲁棒性。A.Ravi等人[10]先将SSVEP信号转换到频域提取特征，再输入到CNN网络，可以有效地降低模型的计算复杂度。

在空间机械臂脑机交互系统中，为保证实际应用中的信息传输效率，有必要在短时间内实现对SSVEP信号的正确分类，因此本文针对1 s时间窗口的6类信号分类问题，提出了一种基于卷积神经网络的SSVEP分类方法，并与传统的CCA和FBCCA方法进行比较，本文方法的平均识别准确率最高。采用本文方法解码6类SSVEP信号，并控制仿真环境下的空间机械臂进行操作。

1 SSVEP信号处理与分类

1.1 SSVEP信号原理

SSVEP信号由视觉刺激产生[11]，当人眼受到外界一个持续性的闪烁刺激时(刺激频率一般高于6 Hz)，大脑枕叶区的视觉皮层会产生相应的信号，该信号的频率与闪烁刺激的频率及其谐波频率相同。SSVEP脑机接口正是根据这个原理设计的。如图1所示，当受试者注视一个频率为10 Hz的周期性持续刺激时，从SSVEP信号的频谱图上可明显看出在10 Hz、20 Hz和30 Hz处出现波峰，波峰的幅值随着频率的增大呈递减趋势。

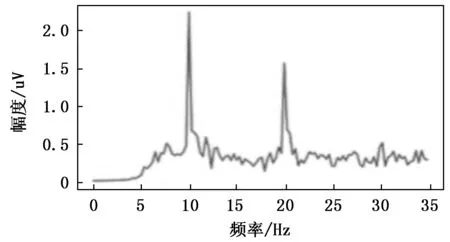
图1 10 Hz频率诱发的SSVEP频谱图

1.2 数据集介绍及预处理

本文所使用的数据来自清华大学的Benchmark数据集[12]，该数据集共采集了35名健康的受试者(记为S01-S35)，其中女性有17名，男性有18名。在所有受试者中，受试者S01-S08有过SSVEP数据的采集经验，受试者S09-S35则没有。该数据集使用64通道的脑电仪对40个目标进行了6次实验，每次实验采集到的有效时间为5 s。经处理后，SSVEP信号的采样频率为250 Hz，并且通过50 Hz的陷波滤波器去除工频干扰。选择8 Hz，9 Hz，10 Hz，11 Hz，12 Hz和13 Hz这6个频率作为6分类的刺激频率。基于经验知识，选择该数据集中位于大脑枕叶区的Pz，PO5，PO3，POz，PO4，PO6，O1，Oz和O2这9个通道的数据。并使用巴特沃斯带通滤波器对选用的SSVEP信号进行滤波。

1.3 构建卷积神经网络

1.3.1 特征提取

特征提取是从原始信号中提取出对分类最有效可靠的特征，进行特征提取可以有效降低数据的维度，并且能够在后续处理使用时简化卷积神经网络的计算复杂度。对于脑电信号，通常采用傅里叶变换、小波变换法等方法提取信号的频域或时频域特征[13]。

在本文中，选择先对SSVEP信号进行特征提取，再把提取的特征输入到CNN进行分类。SSVEP信号频域特征明显，快速傅里叶变换(FFT，fast Fourier transform)可以将信号转换到频域[14]。对原始的SSVEP信号使用快速傅里叶变换可以得到一组复数序列，其中实部代表信号的幅度信息，虚部代表信号的相位信息。研究结果表明，信号的相位信息在解码SSVEP时提供重要信息[15]，因此将快速傅立叶变换的实部和虚部结合起来作为CNN的输入。对每个通道使用分辨率为0.293 0 Hz的标准快速傅立叶变换，选择4～40 Hz之间的频率分量，把计算出的FFT实部和虚部组合成一个新的特征。

再将这些特征按通道顺序进行堆叠，得到最终的特征矩阵。

1.3.2 卷积神经网络

卷积神经网络的研究开始于20世纪80至90年代，经过多年的完善发展，目前已经是深度学习领域中最常用的神经网络之一，在图像处理[16]、信号分类[17]和目标检测[18]等方面都发挥了重要的作用。一个常见的CNN架构包括输入层、隐藏层和输出层这几部分。在隐藏层中，又有卷积层、全连接层等常见的架构。利用CNN进行信号分类时，网络的输入通常是原始时域信号或信号的特征矩阵，通过卷积层对输入的数据加以学习，并由输出层输出分类标签。

在本文中，设计了一个5层的CNN网络，分别是一个输入层，3个卷积层和一个全连接的输出层。总体的网络结构如图3所示，每一层的网络具体如下：

1)输入层l1。第一层为整个网络的输入层，将前一步特征提取中得到的特征矩阵作为整个网络的输入在特征提取中，我们对每一个通道都提取了特征，整个特征矩阵的维度即为通道数×特征数量。在图2中，输入的特征矩阵大小为9×248，表示一共有9个通道的输入数据，每个通道中有248个特征数量。

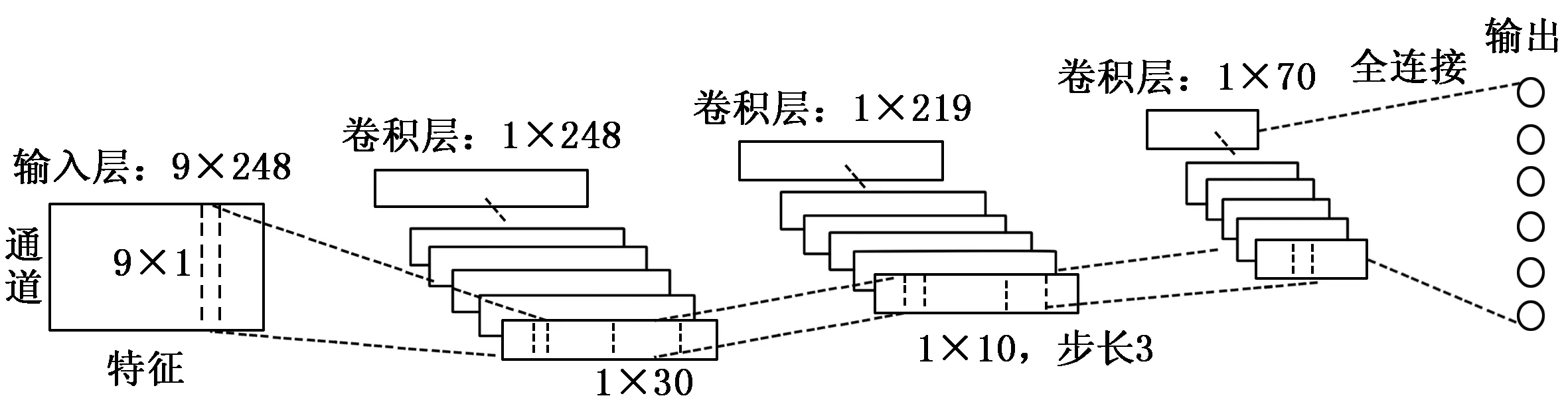
图2 卷积神经网络总体结构图

2)卷积层l2。卷积层l2层执行整个网络中的第一次卷积操作，为学习每个通道的不同作用，参考空域滤波器的设计，在这一层中，利用步长为1，维度为9×1的一维卷积核对输入数据进行卷积。l2层一共输出18个大小为1×248的一维特征图。

3)卷积层l3。第三层是对每张特征图中的频谱特征进行学习，利用步长为1，维度为1×30的卷积核进行卷积。在这一层中只进行有效的卷积，即不对边界数据进行处理，最后输出的特征图数量不变，大小则变为1×219。

4)卷积层l4。卷积层l4是在卷积层l3的基础上对频谱特征再做一次卷积，采用步长为3，维度为1×10的卷积核进行卷积，同样不对边界数据进行处理，共输出18个特征图，每个特征图的大小减小为1×70。为方便将这一层得到的数据传递给输出层，在卷积结束后对所有数据进行扁平化处理。

5)输出层l5。输出层由6个节点组成，代表原始SSVEP数据中的6个刺激频率。将卷积层l4和输出层l5进行全连接，选择使用softmax函数作为输出层的激活函数。

在卷积神经网络的每一层卷积后，选择线性整流函数(ReLU)作为卷积层的激活函数，并且不设置偏置值。研究表明，批归一化可以使特征服从均值为0，方差为1的分布，从而使得网络中的数据分布相对稳定，可以简化调参过程，并起到了一定的正则化效果。为了提高网络的泛化能力，加快模型的学习训练速度[19]，对卷积层l2，l3和l4层的输出均使用批归一化处理。同时，使用权值衰减和随机删除部分神经元的方法可以有效防止训练过程中出现过拟合现象，因此在每一层卷积中引入了L2正则化和dropout方法[20]。

CNN训练时，使用误差反向传播法训练网络。以均值为0，标准差为1的高斯分布作为CNN的权重初始值。训练过程中，利用小批量训练进行学习，每次输入32个数据段，总共迭代50次。损失函数选择使用交叉熵损失函数，采用SGDM算法进行权值优化，设置学习率为0.001，动量为0.9。为防止过拟合，设置正则化项L2为0.000 1，dropout比率为0.2。

1.4 典型相关分析

CCA方法可以计算出两组数据之间的相关程度。其基本原理是分别从两组数据中提取一对综合变量，计算这组变量对之间的相关关系，我们可以得到一个数值，即为这组变量对之间的相关系数。显然，在这两组数据中我们可以提取出很多对综合变量。其中，相关系数最大的一组变量对被称为这两组数据的一对典型变量，相关系数越大，代表这组变量对之间的相关关系就越强，说明两组数据之间的关联性也越强。因此，在分析两组数据之间的整体关系时，可以根据这两个指标来判断。

使用CCA方法进行SSVEP分类时，我们通常只关注SSVEP信号与模板信号之间最大的相关系数，因此通过计算两者之间的典型相关系数就可以确定刺激频率。研究表明，CCA在区分SSVEP信号时具有优异的性能[21]。定义两组变量X和Yi，X为采集到的SSVEP信号，表示为：

X=(X1,X2,...,Xn)

(1)

(2)

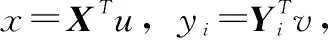
(3)

按上述步骤计算待检测的SSVEP信号与各模板信号之间的皮尔森相关系数，确定目标频率:

ft=maxp(x,yi),i=1,2,...,M

(4)

式中，M为视觉刺激的个数。

1.5 滤波器组典型相关分析

FBCCA是对CCA方法的一种改进[22]，相比于CCA，FBCCA方法有效地利用了信号中的谐波成分。根据CCA的原理，在进行SSVEP信号分类时，更关注SSVEP信号与模板信号之间的相关关系，而忽略了SSVEP内部的谐波信息。从SSVEP的频谱图中可以很清楚地看出，信号中的谐波成分，尤其是二次谐波成分非常明显，因此可以通过这些谐波成分为SSVEP分类提供重要的参考信息。

在进行分类前，先使用滤波器组将SSVEP信号分成多个子带，对每个子带和模板信号进行CCA处理，计算出对应的相关系数。最后，将每个子带得到的相关系数进行加权平方和后求得最终的相关系数：

(5)

式中，i表示某类视觉刺激目标，j表示子带的索引，l为子带总个数，M为视觉刺激的个数，w(j)为子带分量对应的权重因子，可以表示为：

w(j)=j-a+b,j∈[1,j]

(6)

式中，a和b为常数参数，根据经验，通常设置参数a为1.25，参数b为0.25。最终确定目标频率为：

ft=max(pi),i=1,2,...,M

(7)

2 实验分析

将卷积神经网络方法在数据集上的进行测试，由于卷积神经网络需要比较大的数据量，而数据集中的SSVEP信号较少，因此采用数据分割的方式增加数据量[23]。将每个5秒的数据用宽度为1 s，步长为200 ms的滑动窗口进行分割，这样单次试验将能获得21个分段数据，每人每个频率目标一共有126个分段数据，可满足卷积神经网络的数据需求。

更多信息，请扫描二维码关注“老创客”微信公众号。如果您也想展示自己的作品，请拨打电话0551-62607765。

使用卷积神经网络方法进行训练时，将单个受试者的数据按比例划分为训练集和测试集。为得到较好的效果，对每个受试者的数据进行10倍交叉验证，即将数据划分为10份，分别选择其中9份数据作为训练数据，剩余的1份数据作为测试数据。每次试验都会得到一个分类准确率，将10次试验得到的准确率的平均值作为最终的分类准确率。同时使用CCA和FBCCA的方法在该数据集上进行测试，将3种方法得到的分类准确率进行比较，对比的结果如表1所示。

表1 1 s时间窗口下分类准确率对比

实验表明，对35名受试者使用本文提出的卷积神经网络方法，平均分类准确率为99.07%，明显高于CCA方法(41.67%)和FBCCA方法(85.79%)。其中最高的分类准确率为100%(S3，S5，S10，S12，S13，S14，S22，S25，S26，S31，S32)，共11人，占总数的31.43%；最低分类准确率为94.18%(S33)。考虑到数据集中受试者S1-S8有过采集SSVEP数据的经验，而受试者S09-S35则没有，因此对其分别进行讨论。对于有过经验的受试者S1-S8，他们的分类准确率都在99%以上，平均分类准确率达到了99.64%，说明对于有经验的受试者，本文给出的方法可以出色的完成短时间窗口下的SSVEP信号分类问题，且具有较高的鲁棒性。受试者S09-S35没有采集经验，他们的平均分类准确率为98.90%。在的27名受试者中，共有5人的分类准确率低于98%(S11，S18，S19，S29，S33)，占没有采集经验人数的18.52%，只有两人的分类准确率没有达到95%(S19：94.71%，S33：94.18%)，且相差并不大，说明即使是没有经验的受试者，采用本文方法依然可以保持较高的分类准确率。

除了识别准确率，还可以通过信息传输率(ITR，information translate rate)来评价SSVEP脑机接口的性能[24]，ITR表示在一分钟内所能够传输的信息量大小，ITR越大，说明该方法下信息传输率越快。在SSVEP脑机接口中有3个重要的参数指标，分别是待分类的刺激频率数、信号的分类准确率和单次刺激所持续的时间。信息传输率将这3个指标结合起来：

(8)

(9)

式中，B表示一次刺激所传输的信息量，T表示进行一次刺激所持续的时间，N表示所要分类的刺激频率数量，P表示分类准确率。在本文中，共有6个待分类的刺激频率，选用35名受试者的平均识别率作为信号的分类准确率，设定单次刺激所持续的时间为理论时间1秒。通过上述公式，计算出采用卷积神经网络方法时的信息传输率为149.24 b/min，已经达到了一个很高的传输速率。相比于CCA方法(15.04 b/min)和FBCCA方法(99.92 b/min)，采用CNN方法下的信息传输率得到了巨大的提升。总体而言，在针对短时间窗口的SSVEP信号时，本文提出的方法比传统CCA和FBCCA方法在分类准确率和信息传输率上都有了很大的提升，可以有效提高SSVEP脑机接口的分类性能。

3 空间机械臂的脑机交互控制

本文所使用的仿真空间机械臂在VS2017平台上进行运行。首先在3D Studio MAX中绘制空间机械臂的模型，然后使用OpenGL在VS2017平台上对空间机械臂进行重构。6类SSVEP信号的分类识别在Jupyter Notebook中完成，与空间机械臂仿真环境之间采用TCP/IP协议进行信息传输。将使用卷积神经网络方法分类后的结果作为控制信号，控制仿真环境下的空间机械臂运动，仿真实验方案如图3所示。

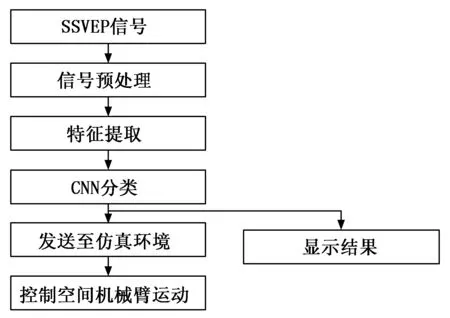
图3 仿真实验方案流程图

仿真环境中的空间机械臂安装在空间站上，由基座、大臂、中臂、小臂和末端手爪等部分组成，其初始示意图见图4。

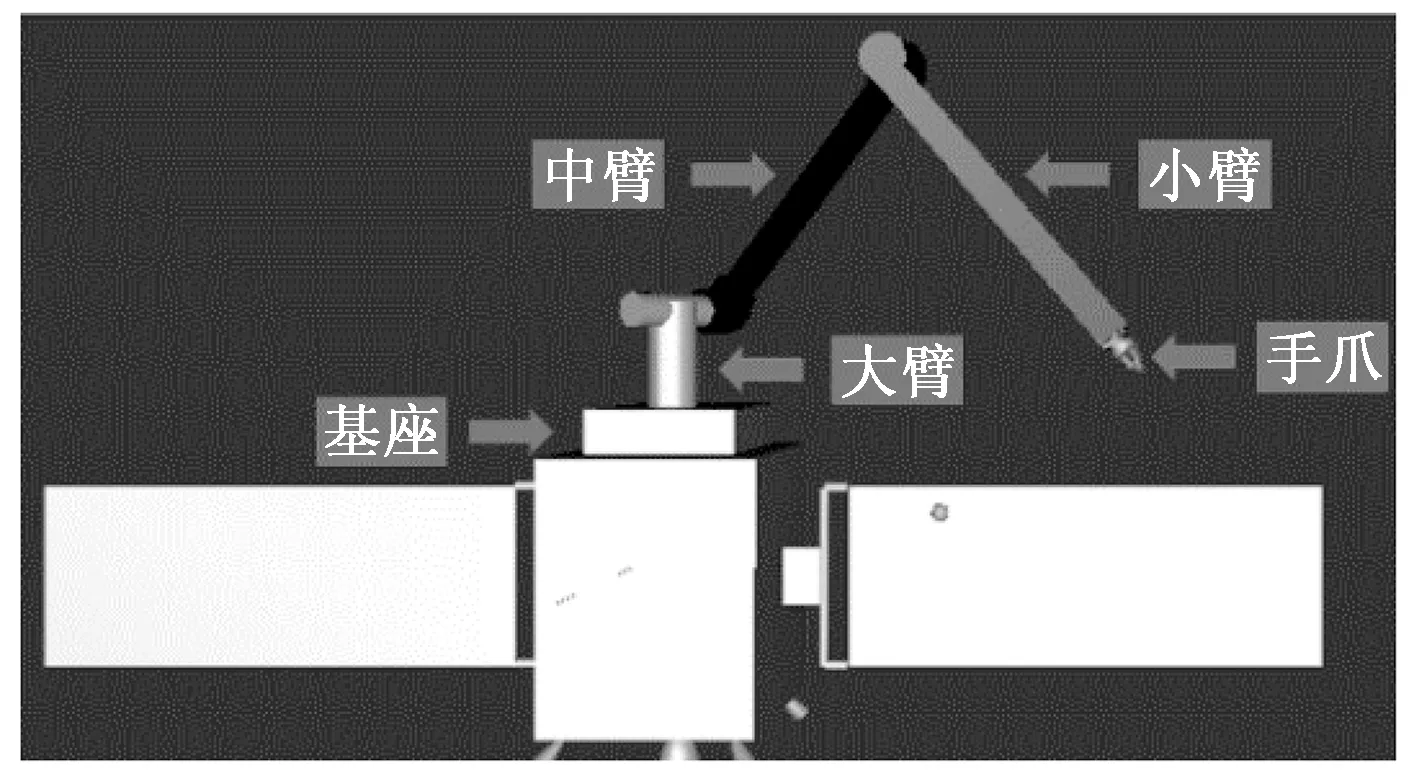
图4 空间机械臂初始示意

操作者利用SSVEP信号解码指令控制空间机械臂，各刺激频率与控制指令和空间机械臂动作的对应关系如表2所示。

表2 刺激目标对应控制指令及机械臂动作

进行仿真实验时，空间机械臂转动示意图见图5。

图5 空间机械臂转动示意图

实验过程中，当检测到受试者注视的刺激频率为8 Hz时，控制空间机械臂大臂顺时针转动；检测到注视的刺激频率为9 Hz时，控制空间机械臂大臂逆时针转动；检测到注视的刺激频率为10 Hz时，控制空间机械臂中臂顺时针转动；检测到注视的刺激频率为11 Hz时，控制空间机械臂中臂逆时针转动；检测到注视的刺激频率为12 Hz时，控制空间机械臂小臂顺时针转动；检测到注视的刺激频率为13 Hz时，控制空间机械臂小臂逆时针转动。

4 结束语

根据实际脑机交互场景中高信息传输率的要求，本文针对短时间窗口下的SSVEP信号分类问题，提出了一种基于卷积神经网络的方法。该方法通过快速傅里叶变换提取各通道的频谱特征并组成特征矩阵，使用卷积神经网络对其进行分类。由于在应用卷积神经网络之前进行了特征提取，本文提出的深度学习网络架构相比于直接对原始SSVEP信号进行深度学习要简单很多。在清华大学的Benchmark数据集上将本文方法与典型相关分析方法和滤波器组典型相关分析方法进行比较，对比结果表明，该方法的目标识别准确率和信息传输率要明显高于另外两种方法。在1秒的时间窗口下，平均识别准确率达到了99.07%，平均信息传输率为149.24 b/min。即使对于没有SSVEP信号采集经验的受试者，应用本文方法的平均识别准确率也达到了98.90%，表示该方法可以有效地对短时间窗口的信号进行分类。最后，采用分类后的SSVEP信号作为控制信号，控制仿真环境中空间机械臂的大、中、小臂运动，验证了本方法是一种可靠的脑机交互方法。

和其他脑电信号相同，SSVEP信号也存在个体差异性强、识别准确率会随着分类目标的增多而下降等缺点，如何使用迁移学习的方法提高模型在不同受试者之间的泛化能力；同时当面对目标更多的分类问题时，保证识别准确率是我们后续研究的重点。