基于小波包分解的AJS-GMDH月径流时间序列预测研究
2022-07-08杨琼波崔东文
杨琼波,崔东文
(1.云南省水文水资源局红河分局,云南 红河 661199;2.云南省文山州水务局,云南 文山 663000)
主要从事水文水资源分析研究和水资源管理保护等工作;崔东文(通讯作者).
径流时间序列预测是水文预报研究领域的热点和难点。提高径流时间序列预测精度对区域水资源开发利用、防洪抗旱规划、水资源管理保护、水库优化调度等具有重要意义。由于径流时间序列人类活动、受气候变化、土地利用及植被覆盖等多重因素的影响,常表现出多尺度、非线性、非平稳性等特征,基于“分解—预测—重构”模式的预测方法被广泛应用于径流时间序列预测[1- 4],并取得了较好的预测效果。目前,常见的时间序列分解方法有经验模态分解(Empirical mode decomposition,EMD)、完全集合经验模态分解(Complete ensemble empirical mode decomposition,CEEMD)、小波分解(Wavelet decomposition,WD)、奇异谱分解(Singular spectrum analysis,SSA)、变分模态分解(Variational mode decomposition,VMD)等;预测模型有BP神经网络、广义回归神经网络(GRNN)、支持向量机(SVM)、相关向量机(RVM)、极限学习机(ELM)、LSTM神经网络、秩次集对分析法等。
WD是一种被广泛应用的时频分析工具,主要通过伸缩平移运算对信号逐步进行多尺度细化,最终达到高频处时间细分,低频处频率细分的目的,已在各领域得到广泛应用。然而,WD不足之处在于其仅对信号低频部分详细分解而忽略了信号的高频部分。小波包分解(Wavelet packet decomposition,WPD)源于WD,它在分解信号低频子集同时,对高频子集继续分解,且能够根据分解需要自行设定分解层数和分解使用的小波函数[5-7],已在各种时序数据分解中得到广泛应用。人工水母搜索(Artificial Jellyfish Search,AJS)算法是Chou等人于2020年基于水母觅食行为而提出一种新型群体智能算法,已在工程结构优化中得到应用[8]。数据分组处理方法(Group method of data handling,GMDH)是针对复杂系统自组织建模的一种前馈型多层神经网络,网络仅通过递阶分层取舍神经元和调整阈值,实现对复杂非线性规律进行拟合,目前已在各种预测研究中得到应用[9-11]。在实际应用中,GMDH网络权值、多项式系数、网络层最大神经元数等参数对GMDH网络预测性能有着重要影响,目前主要有GMDH网络权值优化[12]、多项式系数优化[13]两种途径,而鲜见于针对GMDH网络层最大神经元数、最大网络层数和学习率等关键参数的优化。
本文以云南省龙潭站1952年1月~2016年12月月径流时间序列预测为例,基于WPD、AJS与GMDH网络构建WPD-AJS-GMDH径流时间序列预测模型。内容安排如下:①利用WPD及对比分解方法CEEMD、WD将月径流时间序列数据分解为若干子序列分量;②介绍AJS算法,在不同维度条件下通过6个典型函数对AJS算法进行仿真验证,采用AJS优化GMDH网络层最大神经元个数、最大网络层数、学习率、选择压力系数,构建WPD-AJS-GMDH模型,并构建WPD-AJS-SVM、WPD-AJS-BP、WPD-GMDH、WPD-SVM、WPD-BP、CEEMD-AJS-GMDH、CEEMD-AJS-SVM、CEEMD-AJS-BP、CEEMD-GMDH、CEEMD-SVM、CEEMD-BP和WD-AJS-GMDH、WD-AJS-SVM、WD-AJS-BP、WD-GMDH、WD-SVM、WD-BP作对比分析模型;③利用所构建的18种模型对实例月径流时间序列进行检验。
1 研究方法
1.1 小波包分解(WPD)
WPD是在小波分解(WD)的基础上改进和发展而来的一种有效分解方法,能同时对高频、低频部分实施信号分解。理论上,3层小波包分解能够提取绝大部分信号中的有效信息,逼近任意非线性函数,从而达到解决实际问题的目的。小波包分解算法公式[14-16]为
(1)
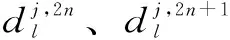
重构算法为
(2)
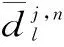
1.2 人工水母搜索(AJS)算法
1.2.1 AJS算法数学描述
AJS算法是基于水母觅食行为而提出一种新型元启发式算法。该算法通过模拟水母洋流移动、群内移动(主动移动和被动移动)和移动切换策略来达到求解优化问题的目的。AJS算法基于3个理想化规则:①水母要么跟随洋流移动,要么在群内移动,“时间控制策略”控制着两种移动之间的切换;②水母在海洋中寻找食物,他们更容易吸引到食物丰富的区域;③找到的食物数量取决于水母位置及其相应的目标函数值[7]。
AJS算法数学描述简述如下[7]:
(1)洋流移动。AJS通过计算海洋中每只水母到当前最佳水母位置的平均矢量值确定洋流方向(趋势)。 洋流移动数学描述
(3)
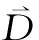
(4)

表1 AJS算法标准测试函数寻优结果
式中,Xi(t+1)为第i只水母第t+1次迭代位置;Xi(t)为第i只水母第t次迭代位置;其他参数意义同上。
(2)水母群移动。在水母群中,水母分为被动移动(A型)和主动移动(B型)两种类型。当水母群刚形成时,大多数水母呈A型移动;随着时间推移,大多数水母呈B型移动。A型移动表示水母在其自身位置周围移动,其位置更新公式为
Xi(t+1)=Xi(t)+γ×rand(0,1)×(Ub-Lb)
(5)
式中,γ为运动系数,本文取0.1;Ub、Lb分别为搜索空间上、下限值;其他参数意义同上。B型运动描述为:当水母Xj所处区域食物量超过水母Xi所处区域食物量时,水母Xi向水母Xj移动;反知,水母Xi远离水母Xj。其位置更新公式描述如下
(6)
式中,Xj(t)为第j只水母的第t次迭代位置;f(Xi)、f(Xj)分别为水母Xi、水母Xj的适应度值;其他参数意义同上。
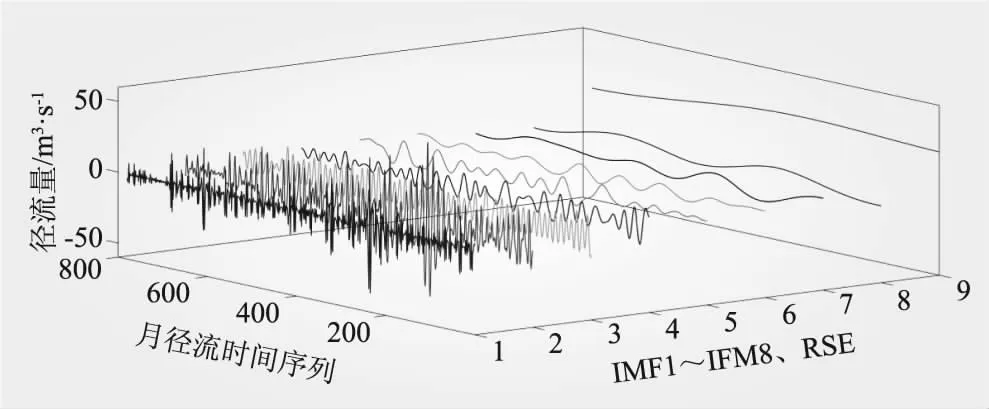
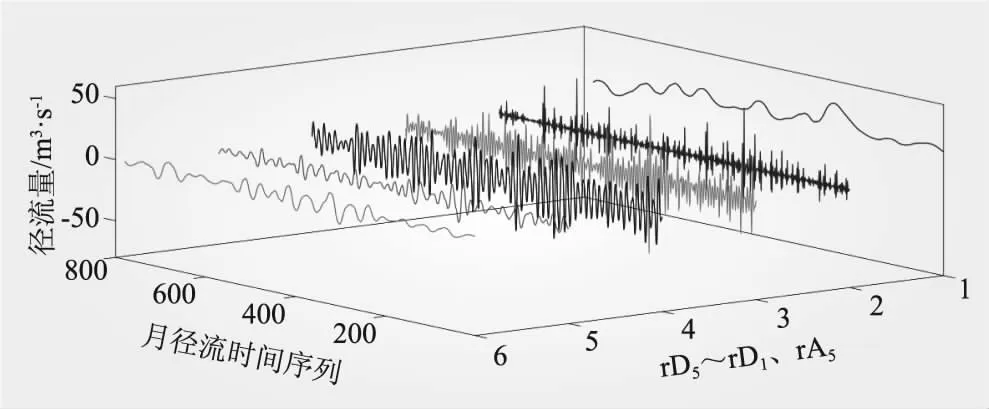
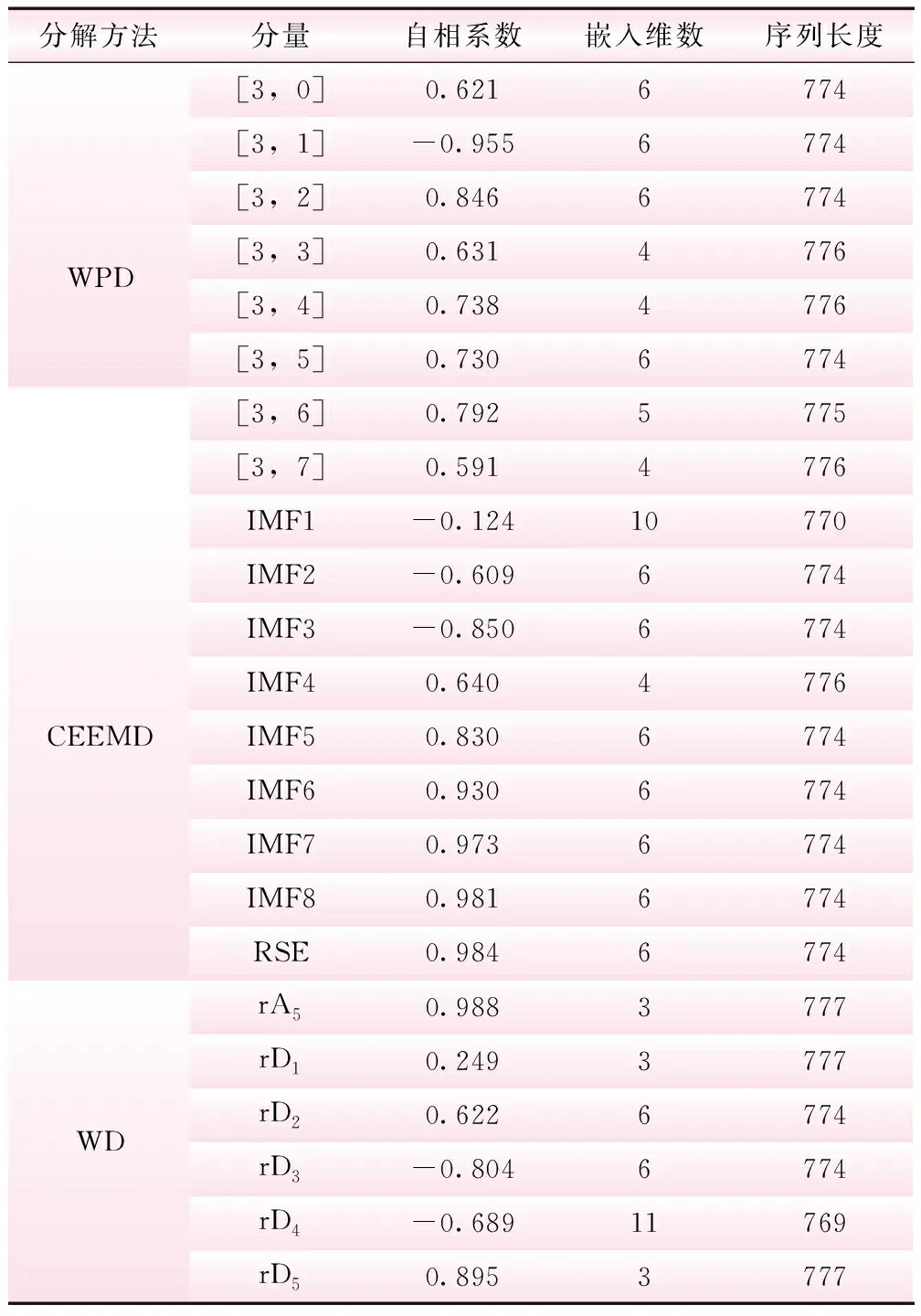
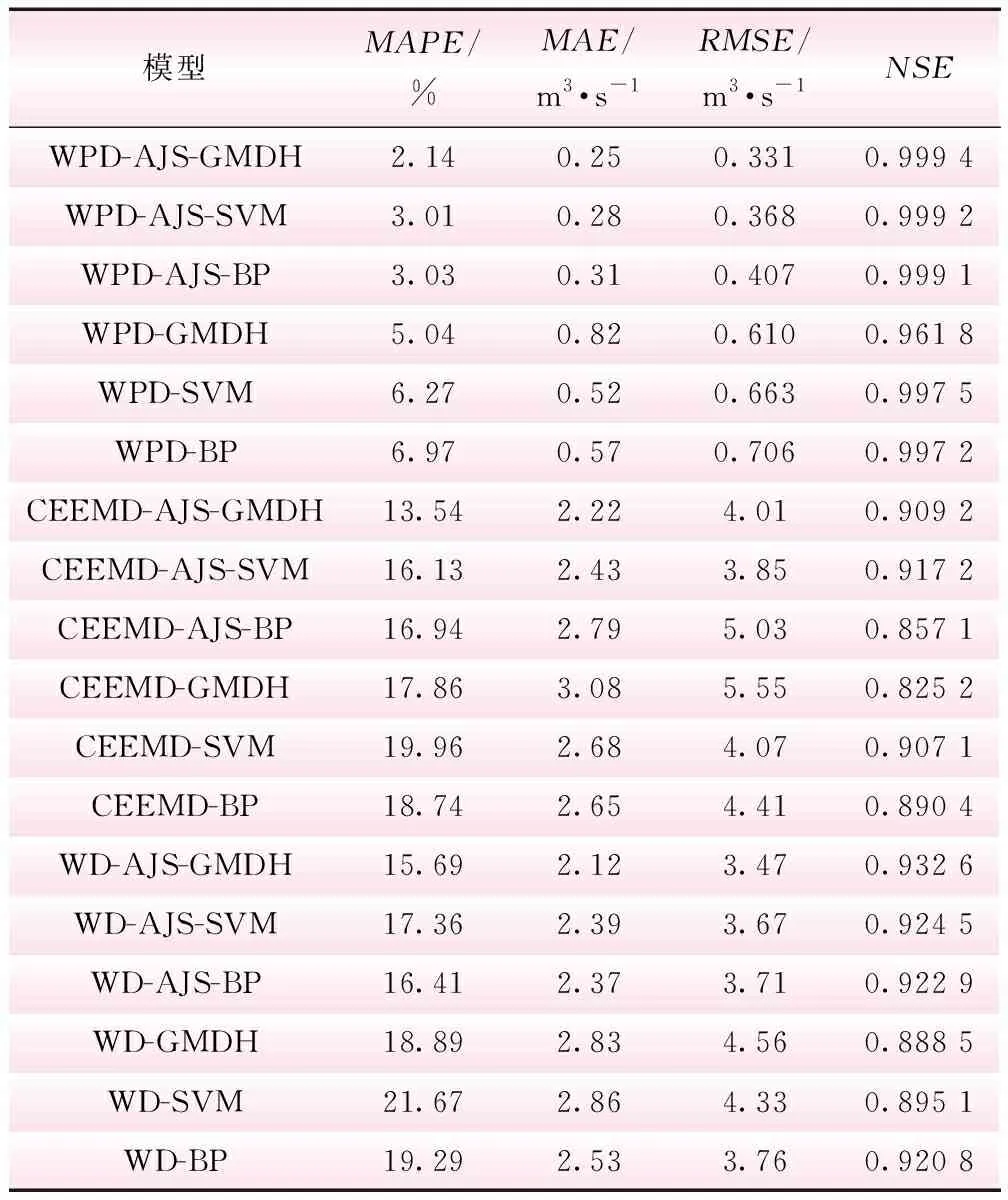
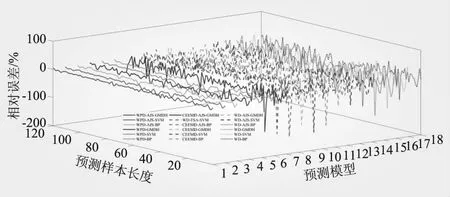
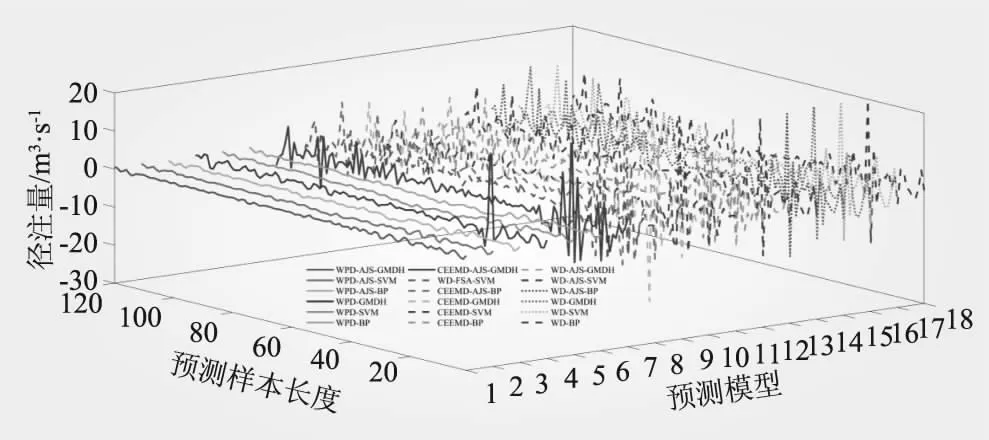
(3)时间控制切换策略。水母在水母群中的运动分为A型和B型,为更好地模拟水母在这两种移动之间的切换,引入时间控制函数c(t)来描述这种情况,当c(t)≥c0时,水母跟随洋流移动;当c(t) c(t)=|(1-t/Tmax)×[2×rand(0,1)-1]| (7) 式中,t为当前迭代次数;Tmax为算法最大迭代次数;c0为时间控制常数,本文取0.5。 1.2.2 AJS算法仿真验证 在不同维度条件下,选取Sphere等6个测试函数对AJS算法进行仿真验证(见表1)。AJS算法通过Matlab 2018a M语言实现,利用函数20次寻优平均值评估AJS算法的性能。设置AJS算法最大迭代次数Tmax=3 000,种群规模npop=100。 对于单峰函数,AJS算法在不同维度条件下20次寻优精度均在7.20×10-83以上,表现出较好的寻优精度;对于多峰函数,AJS算法在不同维度条件下20次寻优精度均在1.22×10-12以上,具有较好全局寻优能力。可见,对于表1中的函数,在不同维度条件下AJS算法均表现出较好寻优效果。 GMDH网络是针对复杂系统自组织建模的一种前馈型多层神经网络,也称多项式网络,目前已在电主轴热位移[17]、经济短期预测[18]、碳价格预测[19]、潮汐预报[20]、用户流失预测[21]等方面得到应用。GMDH网络由系统各输入单元交叉组合产生活动神经元,从已产生的一代神经元中选择若干与目标变量最接近的神经元,通过强强结合再次产生新的神经元,……。通过重复这一优胜劣汰和逐渐进化的过程,直到获得外准则值最低的最优神经元,即完成GMDH网络模型训练过程[9-11]。 yi=f(xi1,xi2,…,xin),i=1,2,…,N (8) 式中,yi为实际输出;xi1,xi2,…,xin为输入;N为输入变量的数量。 (9) (10) 在GMDH预测过程中,除网络权值、多项式系数对GMDH预测效果产生直接影响外,GMDH网络层最大神经元数、最大网络层数、学习率等关键参数对GMDH网络预测性能同样具有重要影响。为进一步提升GMDH网络预测性能,拓展GMDH网络优化方向,本文利用AJS算法对GMDH网络层最大神经元数、最大网络层数、学习率、选择压力系数进行优化,以期进一步提高GMDH网络预测性能。 WPD-AJS-GMDH模型预测实现如下: 步骤一,利用WPD将原月径流时间序列分解为8子序列分量[3,0]~[3,7]。利用自相关函数法(AFM)确定各子序列分量的输入、输出向量,合理划分训练、预测样本[22],见图1。 步骤二,构建训练样本均方误差作为AJS-GMDH模型适应度函数 (11) 步骤三,设置AJS算法水母种群规模npop、最大迭代次数Tmax和算法终止条件。利用式(12)初始化水母空间位置Xi(i=1,2,…,npop),则 Xi+1=ηXi(1-Xi),0≤X0≤1 (12) 式中,Xi为第i只水母位置的logistic混沌值;X0用于生成水母的初始种群,X0∈(0,1),且X0∉{0.00,0.25,0.50,0.75,1.00 };参数η设置为4.0。 步骤四,计算每只水母Xi适应度值,找到并保存最佳水母适应度fbest和最佳水母个体位置X*。 步骤五,利用式(7)计算时间控制函数c(t)。若c(t)≥0.5,利用式(4)更新水母位置;否则,利用式(5)、(6)更新水母位置。 步骤六,计算当前每只水母Xi适应度值;比较并保存当前最佳水母适应度值fbest和最佳水母个体位置X*。 步骤七,判断算法是否达到终止条件,若是,则输出最佳水母个体位置X*,算法结束。 步骤八,输出最佳水母个体位置X*。即,GMDH网络层最大神经元数、最大网络层数、学习率、选择压力系数;利用AJS-GMDH模型对分量[3,0]~[3,7]进行预测,叠加重构后即得到实例月径流最终预测结果。 步骤九,利用平均绝对百分比误差(MAPE)、平均绝对误差(MAE)、纳什系数(NSE)和均方根误差(RMSE)对各模型有效性进行评估。即 (13) 图1 实例月径流预测流程 龙潭站位于云南省文山市攀枝花镇龙潭寨村,系红河流域泸江水系盘龙河干流控制站,控制径流面积3 128 km2,为我国重要的水文站和中央报汛站。 2.1.1 WPD分解 基于demy小波包基,利用WPD将龙潭站1952年1月~2016年12月逐月径流数据进行3层小波包分解,得到8个子序列分量数据,见图2。 从图2来看,[3,0]~[3,3]为低频空间数据波形,振幅较大、波长较短,大致反映月径流时间序列的变化趋势;[3,4]、[3,5]、[3,6]、[3,7]为高频空间数据波形,从[3,4]分量到[3,7]分量,其振幅逐渐减小、波长逐渐变长,大致反映月径流时间序列的波动情况[4]。 2.1.2 CEEMD分解 利用CEEMD方法对龙潭站实例月径流数据进行分解,分解结果见图3。从图3可以看出,高频子序列RSE的频率最高、幅度最大、波长最短;中频子序列IMF4~IMF8和低频子序列IMF1~IMF3的振幅逐渐减小,频率逐渐降低,波长逐渐增大,周期性逐渐增强,符合经验模态分解规律[18]。 2.1.3 WD分解 利用db5小波将龙潭站实例月径流数据进行分解,得到1个低频率分量rA5和5个高频率分量rD1、rD2、rD3、rD4、rD5,见图4。从图4可以看出,高频分量反映原始数据的变化特征,低频分量反映原始数据的变化趋势。 图2 实例月径流时间序列WPD分解3D效果 图3 实例月径流时间序列CEEMD分解3D效果 图4 实例月径流时间序列WD分解3D效果 本文采用自相关函数法(AFM)确定各分量的输入、输出向量,即通过计算各子序列分量的自相关系数,在滞后数≥3情况下,选取自相关系数最大时所对应的滞后数作为各子序列分量最优输入维数,通过最优输入维数构建预测模型输入、输出向量,见表2。本文利用实例前649~657个月径流数据作为训练样本,后120个月作为预测样本[4]。 表2 各分量自相关系数、输入维数及序列长度 从表2可以看出,经WPD分解的各子序列分量自相关系数绝对值均在0.591以上;经CEEMD分解的IMF1分量、经WD分解的rD1分量自相关系数绝对值小于0.25,这在很大程度上制约分解效果和预测精度。 2.3.1 参数设置 (1)WPD-AJS-GMDH、WPD-GMDH、CEEMD-AJS-GMDH、CEEMD-GMDH、WD-AJS-GMDH、WD-GMDH模型:设置WPD-GMDH、CEEMD-GMDH、WD-GMDH模型网络层最大神经元数m=20;最大网络层数r=5;选择压力系数α=0.6;学习率p=0.85;WPD-AJS-GMDH、CEEMD-AJS-GMDH、WD-AJS-GMDH模型AJS算法最大迭代次数Tmax=50,种群规模npop=30;网络层最大神经元数m搜索空间[5,50],最大网络层数r搜索空间[2,10],选择压力系数α搜索空间[0.01,0.9],学习率p搜索空间[0.01,0.9],其他采用默认值。 (2)WPD-AJS-SVM、WPD-SVM、CEEMD-AJS-SVM、CEEMD-SVM、WD-AJS-SVM、WD-SVM模型:WPD-SVM、CEEMD-SVM、WD-SVM模型惩罚因子、核函数参数和不敏感损失系数通过人工试凑法确定;WPD-AJS-SVM、CEEMD-AJS-SVM、WD-AJS-SVM模型AJS算法最大迭代次数Tmax=50,种群规模npop=30;不敏感损失系数、惩罚因子、核函数参数搜索空间分别设置为[0.001,1]、[0.01,100]、[0.01,100],输入数据采用[0,1]进行归一化处理。 (3)WPD-AJS-BP、WPD-BP、CEEMD-AJS-BP、CEEMD-BP、WD-AJS-BP、WD-BP模型:设置WPD-BP、CEEMD-BP、WD-BP模型隐层传递函数、输出层传递函数、训练函数分别为tansig、purelin、trainlm,设定期望误差0.000 001,最大训练轮回1 000次,隐层节点数为输入维数的2倍减1;WPD-AJS-BP、CEEMD-AJS-BP、WD-AJS-BP模型AJS算法最大迭代次数Tmax=50,种群规模npop=30,权值阈值搜索空间∈[-1,1],BP部分设置同WPD-BP、CEEMD-BP、WD-BP模型。输入数据采用[0,1]进行归一化处理。 2.3.2 实例预测结果分析 基于表2构建各分量的输入、输出向量,并利用所建立的WPD-AJS-GMDH等18种模型对各分量进行预测,将预测结果叠加重构后即得到实例月径流最终预测结果。各模型采用上述MAPE、MAE、RMSE、NSE进行评估,结果见表3,预测效果见图5、6。 由表3及图5、6可以得出以下结论: (1)WPD-AJS-GMDH、WPD-AJS-SVM、WPD-AJS-BP模型的预测效果优于WPD-GMDH、WPD-SVM、WPD-BP模型,远优于其他模型。其中,尤以WPD-AJS-GMDH模型预测的精度最高、效果最好,其平均绝对百分比误差2.14%,平均绝对误差0.25 m3/s,纳什系数0.999 4,均方根误差0.331 m3/s。将WPD-AJS-GMDH模型用于月径流时间序列预测是可行和可靠的,模型具有更高的预测和更好的泛化能力。 (2)从不同分解方法预测结果对比来看,基于WPD分解的同种模型的预测效果要远优于基于CEEMD、WD分解的同种模型,表明WPD对月径流时间序列的分解效果要优于CEEMD、WD方法。 表3 实例月径流时间序列预测结果对比 图5 实例月径流时间序列预测相对误差3D 图6 实例月径流时间序列预测绝对误差3D (3)基于AJS算法优化的同种模型的预测效果要优于未经AJS算法优化的同种模型,表明AJS算法能有效优化GMDH网络层最大神经元数、最大网络层数、学习率和选择压力系数,以及SVM惩罚因子、核函数参数、不敏感损失系数和BP网络权阈值,有效提高GMDH网络、SVM、BP网络的预测性能。 (4)从图5、6可看出,WPD-AJS-GMDH模型预测的绝大多数样本绝对百分比误差、平均绝对误差均在0值附近波动,具有较优的预测效果;次之为WPD-AJS-SVM、WPD-AJS-BP模型;再次为WPD-GMDH、WPD-SVM、WPD-BP模型,其他12种模型则均较差。 本研究将WPD、AJS与GMDH网络进行结合,构建WPD-AJS-GMDH月径流时间序列预测模型,利用云南省龙潭站1952年1月~2016年12月共780组月径流时序数据进行实证分析,并建立基于CEEMD、WD分解的GMDH、SVM、BP模型做对比分析。结果如下: (1)在不同维度条件下,AJS算法均具有较好的寻优效果,将AJS算法用于GMDH网络层最大神经元数、最大网络层数、学习率和选择压力系数寻优是可靠的。 (2)WPD-AJS-GMDH模型对实例后120个月月径流时间序列预测的平均绝对百分比误差为2.14%,平均绝对误差为0.25 m3/s,纳什系数0.999 4,均方根误差0.331 m3/s,预测效果略优于WPD-AJS-SVM、WPD-AJS-BP模型,优于WPD-GMDH、WPD-SVM、WPD-BP模型,远优于其他模型。将WPD-AJS-GMDH模型用于月径流时间序列预测是可行和可靠的,模型具有更高的预测和更好的泛化能力。 (3)实例验证表明,WPD能将径流时序数据分解为更具规律的子序列分量,有效弱化复杂环境对径流时间序列的影响,降低预测复杂度,其分解效果明显优于CEEMD、WD方法。 (4)实例验证表明,AJS算法能有效优化GMDH网络层最大神经元数、最大网络层数、学习率和选择压力系数,不但克服了GMDH网络人工选择关键参数的不足,而且大大提高了GMDH网络的预测精度和智能化水平,具有较好的实用价值。1.3 GMDH网络
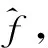
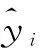
1.4 建模流程
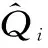
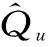
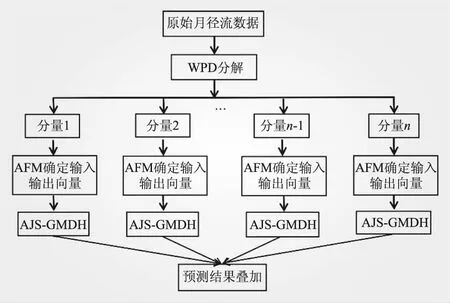
2 实例应用
2.1 时序数据分解

2.2 时间序列建模
2.3 参数设置及预测分析
3 结 论
