基于K近邻与主成分分析的短时交通流预测
2022-07-08李翠,黄侃,李霞
李 翠, 黄 侃, 李 霞
(江西交通职业技术学院 信息工程学院, 南昌 330013)
交通流数据为智能交通系统ITS(Intelligent Transportation System)的正常运行提供了数据支撑,其中蕴含的交通时空分布规律对现代交通的科学管理与决策、交通流的基础理论研究具有重要利用价值[1]。ITS已在世界范围内广泛应用,并成为了高速公路和城市道路交通控制的有力工具。为了实现有效的交通控制和交通诱导,需在做出控制(诱导)变量决策的时刻对下一决策时刻乃至以后若干时刻的交通流量做出实时、准确的预测(即短时交通流预测)。短时交通流预测一般不超过15 min的时间跨度[2]。
有关短时交通流预测的算法大致可划分为3类[3-10]:第一类是基于传统数理统计模型的算法,也可称为参数法,主要包括历史均值法[3]、时间序列法[4]、卡尔曼滤波法[5]等。该类算法模型简单、编程方便,但受交通流非线性和随机性的影响,此类算法在较短预测周期下的预测精度较差。第二类是基于人工智能模型的算法,又称为非参数法,主要包括神经网络法[6]、非参数回归法[7]、支持向量机法[8]等。该类算法可充分逼近任意复杂的非线性和随机性交通流序列,对短时交通流具有较好的预测效果,但存在参数设置困难、收敛速度慢等不足。第三类是基于混合模型的算法,即将前2类算法中的2个或多个预测模型进行组合[9-10]。该类算法依赖于不同模型之间的协调,有利于预测精度的提高,但其参数调整依然是个难题。
K近邻(K-nearest neighbors,KNN)是一种常用的非参数回归方法,KNN法完全由数据驱动而无需假设数据的分布模式,原理简单且易于扩展[11-12]。相关研究主要针对状态向量构造、近邻距离计算和近邻权重选取等关键问题展开,取得了较多成果[13-14]。主成分分析PCA(Principle component analysis)是一种统计方法[15],该方法通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量称为主成分。任意向量均可表达为主成分的线性组合,组合系数则反映主成分对该向量的贡献程度。现有方法一般将PCA结合智能算法进行短时交通流预测[16],同样存在参数难以确定和收敛速度慢等问题。
本文将KNN法和PCA法相结合,提出用于短时交通流预测的KNN-PCA法,以期提供新的研究思路。
1 KNN法基本原理
1.1 计算流程
KNN法完全由数据驱动,通过搜索历史数据库来寻找具有合适数量的、与当前数据相似的多个近邻,并对近邻数据进行加权组合以实现预测功能。KNN法的基本流程如下:1) 构造具有较大容量且有代表性的历史数据库;2) 设定合适的状态向量;3) 计算当前交通流状态向量与历史数据状态向量之间的距离;4) 设定距离阈值后确定近邻个数k;5) 计算近邻权重;6) 对k个近邻进行加权计算以获得预测值。
由以上基本流程可知,KNN法的预测性能取决于状态向量的构造方式、距离的度量方式、近邻的筛选规则和近邻权重的计算方法。
1.2 状态向量的构造
当前交通流的状态向量为:
A=[at-p+1at-p+2…at-1at]T
(1)
式中:ai为第i个时刻采集的交通流量数据;p为状态向量长度;T表示转置。
相应地,设定历史数据状态向量为:
Hi=[hi,t-p+1hi,t-p+2…hi,t-1hit]Ti=1,2,…,q
(2)
式中:hij为第i个历史数据状态向量在第j个时刻采集的交通流量数据;q为历史数据状态向量的数量。
1.3 近邻的筛选指标
常用欧式距离来匹配当前交通流和历史数据的状态向量,以便筛选用于短时交通流预测的近邻。当前交通流状态向量与第i个历史数据状态向量之间的欧式距离为:
(3)
由于相关系数更能反映状态向量的相似性,有利于判断相似交通流,因此采用相关系数来代替欧式距离进行近邻的筛选。当前交通流状态向量与第i个历史数据状态向量之间的相关系数为:
(4)
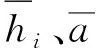
根据式(3)或式(4),可将欧式距离最小或相关系数最大的k个历史数据状态向量视作当前交通流状态向量的近邻。
1.4 交通流量的预测
根据所挑选的近邻来确定第t+1时刻的交通流量预测值:
(5)
式中:αi为第i个近邻的权重;k为近邻数量;hi,t+1为第i个近邻在第t+1时刻的实测交通流量。历史均值法和距离倒数法计算距离权重的公式分别为:
αi=1/k
(6)
(7)
2 KNN-PCA法基本原理
2.1 计算原理
将所有近邻均延拓至第t+1时刻,得到新的向量为:
(8)
通过奇异值分解,对这些近邻延拓向量进行PCA[15],即
(9)
式中:U= [u1u2…up+1]为由特征向量组成的酉矩阵,或称主成分矩阵;S= diag (S1,S2, …,Sp+1)为对角矩阵;Si为特征值,且S1≥S2≥ … ≥Sp+1≥ 0(i=1,2,…,p+1)。
将当前交通流状态向量也延拓至第t+1时刻,得到新的向量为:
Ae=[at-p+1at-p+2…atat+1]T
(10)
进一步将Ae近似表达为前m阶起主要贡献的主成分的线性组合,即
Ae=[u1u2…um]β=Umβ
(11)
式中:β为主成分组合系数构成的列向量;Um为由前m阶起主要贡献主成分构成的矩阵。由于at+1为待预测值,因此基于已测的p个数据,得到式(11)的最小二乘解为:
(12)
利用式(12)计算的组合系数对Ae′进行重构,得到:
Ae′=Umβ
(13)
Ae′中最后一个元素即为第t+1时刻的预测值at+1,其表达式为:
at+1=Ae′(end)
(14)
式中:end表示取最后一个元素。
由式(12)、式(13)可知,PCA法其实提供了一种新的近邻权重计算方法。与历史均值法式(6)和距离倒数法式(7)提供的经验公式不同,PCA法提供了自适应公式,即近邻权重根据主成分的贡献进行自动计算。
2.2 计算流程
KNN-PCA法的计算流程为:
1) 按式(1)、式(2)构造状态向量;
2) 按式(4)计算相关系数;
3) 挑选相关系数最大的前k个历史数据作为近邻;
4) 基于式(8)、式(9)计算主成分;
5) 采用式(12)计算主成分组合系数;
6) 利用式(13)、式(14)计算预测值。
3 评价指标
采用以下3种常用的评价指标来衡量各种算法的预测精度,包括均方根误差(RMSE)、平均误差(MAE)和平均百分比误差(MAPE),表达式分别为:
(15)
(16)
(17)
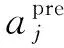
4 算例分析
4.1 数据来源与处理
以明尼苏达大学交通数据研究实验室(TDRL)在2018年1月12日—2019年1月12日(共366 d)采集的交通流量数据(第250号测点)为例展开分析[17]。原始数据的采样间隔为30 s,每d共有2 880个采样点。经统计,共有335 d未出现异常数据。将这些正常数据按15 min采样间隔重新整理(共有96个采样点),并将前334 d的数据作为历史数据,将最后1 d的数据作为测试数据。
4.2 参与比较的预测算法
为更好地比较预测性能,考虑6种不同的KNN算法,如表1所示。算法1~3采用相关系数式(4)来筛选近邻,而算法4~6则采用欧式距离式(3)。算法1即为本文提出的KNN-PCA法。6种算法的计算流程均可参照2.4节执行。

表1 6种交通流预测算法
4.3 近邻数k的取值
在筛选近邻时,每个预测时刻对应的最优k值(即近邻数)往往难以预先确定,故采用动态方法确定k值。对算法1~3,按式(4)计算相关系数,并将相关系数大于0.95的历史数据视作近邻,且k值至少取5,至多取10。算法4~6的k值与算法1~3的相同。对算法4~6,按式(3)计算欧式距离,并将欧式距离最小的k个历史数据取为近邻。
4.4 主成分分析
以算法1为例,设定状态向量长度p=35,并随机选取测试数据第15、48、72和91个预测时刻进行主成分分析。根据式(9)进行奇异值分解后,各得到35阶特征值(由大到小排序),并将其对最大值归一化。将前10阶归一化特征值列于表2,其余未列出的值均小于0.000 001。由表2可知,对所有预测时刻,第1阶特征值均远大于其他阶特征值。这表明第1阶主成分对这些近邻的贡献最大,反映了它们共同的主要变化趋势。
若将阈值设为0.000 001,则归一化特征值大于该阈值的那些主成分对延拓后的状态向量起主要贡献。这4个预测时刻起主要贡献的主成分数量m分别为10、10、5和9。根据式(12)计算这些主成分对当前交通流状态向量的组合系数,如表3所示。
由表3可知,第1阶主成分远比其他主成分的组合系数要大。此外,其他阶主成分的组合系数(绝对值)并不完全与表1所示的特征值排序相同。这是由于特征值大小反映的是主成分对所有近邻共同变化趋势的贡献,而组合系数则仅反映主成分对当前交通流变化趋势的贡献。
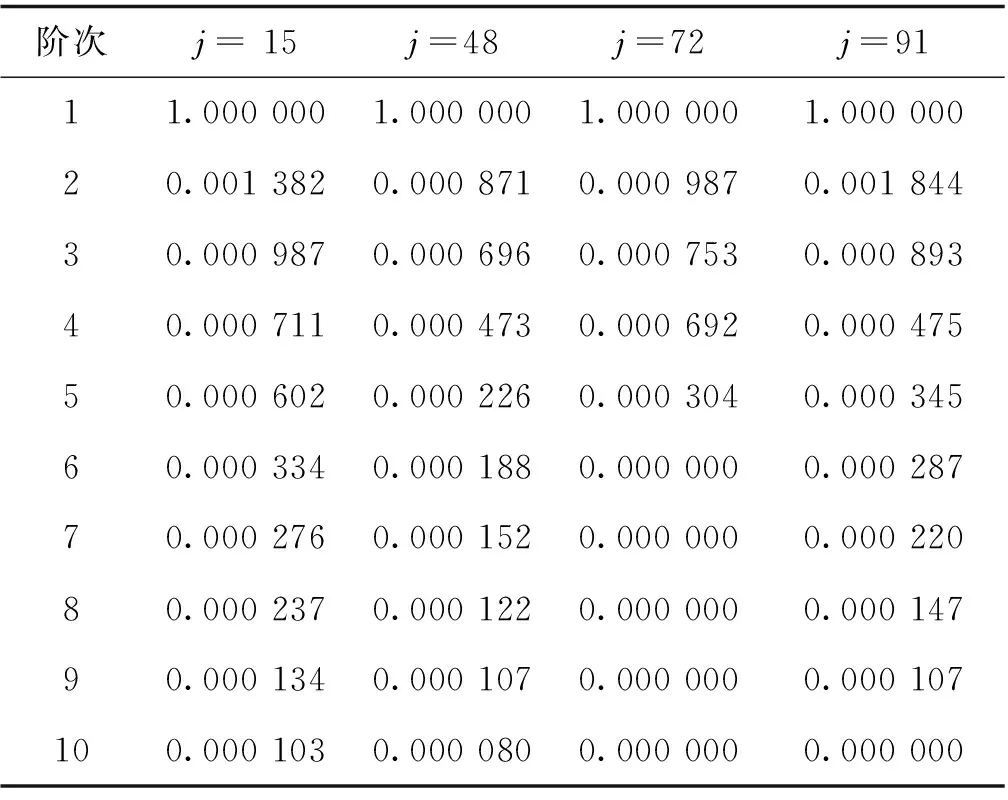
表2 前10阶归一化特征值(算法1)

表3 前m阶主成分对当前交通流状态向量的组合系数
4.5 预测结果
按照4.3、4.4节所述方法确定近邻数k值和起主要贡献的主成分数量m值,并改变状态向量长度p。分别计算6种算法的预测结果,并将3种评价指标RMSE、MAE和MAPE随p值的总体变化趋势和局部变化趋势分别绘于图1、图2。
由图1可知,在p较小时,算法1~4的3种评价指标均较差,且波动很大;算法5~6的评价指标相对较好,但依然存在一定波动。随着p的增大,所有算法的3种评价指标波动范围逐渐收窄且趋于稳定。由图2可知,没有哪种算法能够在所有评价指标中一直保持最佳。比如,算法6在p介于48~72之间时具有最小的RMSE,但却具有较大的MAE和MAPE。这说明,难以确定合适的p值让某种算法在所有评价指标上均表现最佳。
总的来说,算法1在p=32~96时波动较为平稳,特别是在p=93~96时,3种评价指标均较小。相比其他算法,算法1的3种指标在p=93~96时也均最佳。因此,在采用算法1进行计算时,可将状态向量长度p取为96,即与每d的数据长度相同。
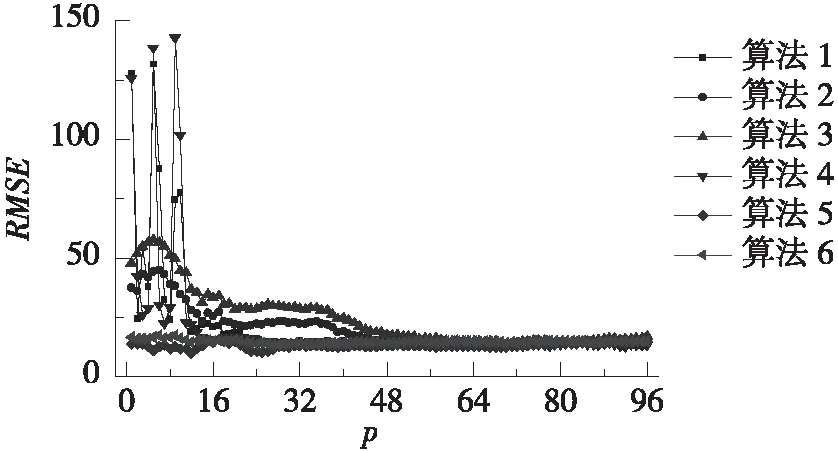
(a) RMSE指标

(b) MAE指标
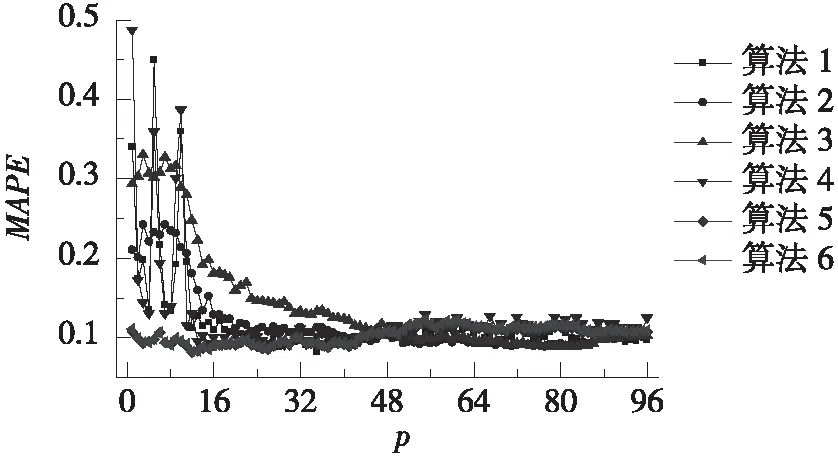
(c) MAPE指标
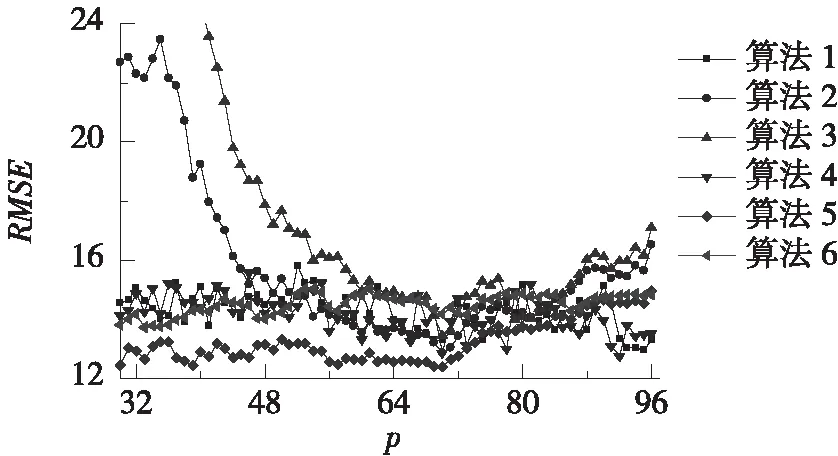
(a) RMSE指标(局部放大)
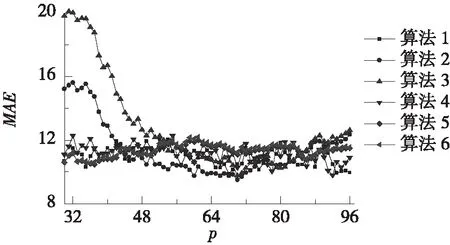
(b) MAE指标(局部放大)
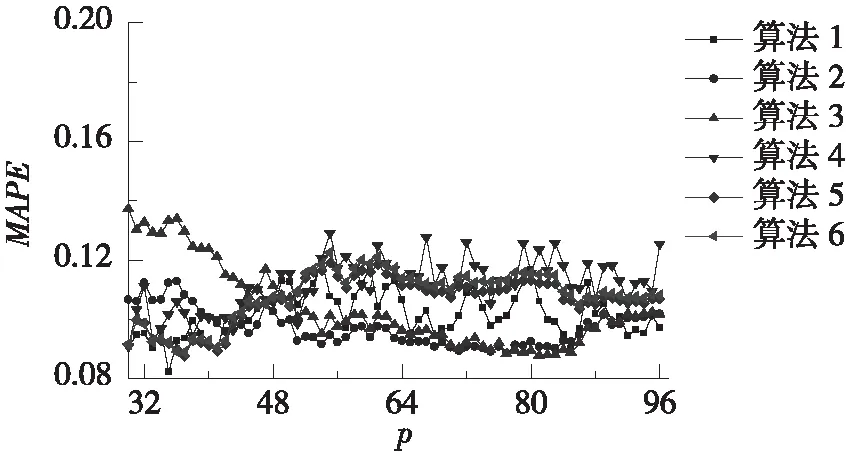
(c) MAPE指标
6种算法在p=48、72、96时的预测结果如图3所示。不难发现,算法1、算法4能很好地反映真实交通流的总体变化趋势,尤其在交通流量较大的时间段(j=40~72时),这2种算法的预测值与真实值更为吻合。注意到算法1、算法4均对近邻进行了PCA,这表明PCA有利于预测交通流的总体变化趋势。但也应当注意,在交通流变化较为剧烈的时刻(如j=67、68),算法1、算法4的预测结果跟真实值依然存在一定偏差,这种现象是因交通流存在较大的随机性所致。
进一步比较算法1、算法4在p=48、72、96时的评价指标如图2所示,由此可知算法1总体上比算法4的预测性能更好一些,这表明采用相关系数比采用欧式距离来筛选近邻更有利于保证KNN-PCA法的短时交通流预测精度。
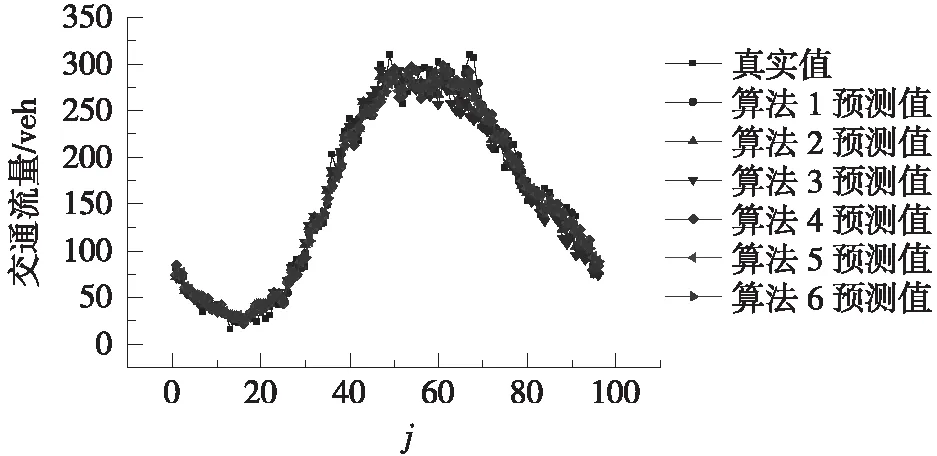
(a) p=48
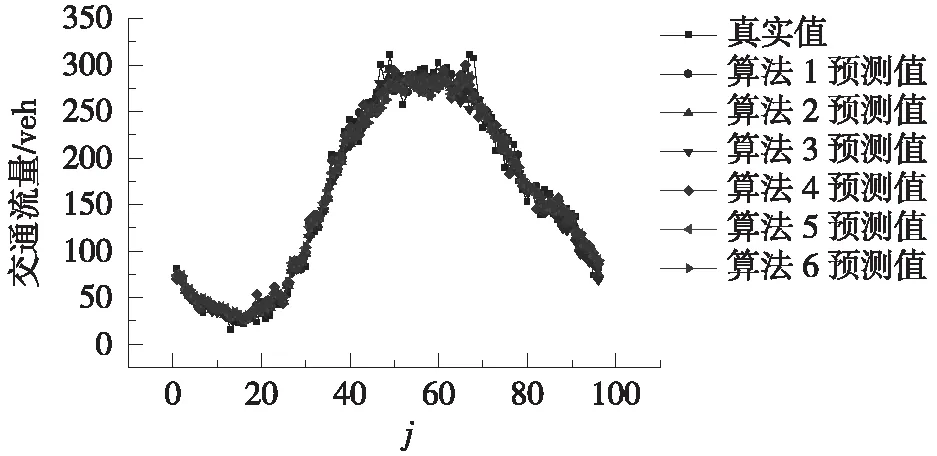
(b) p=72
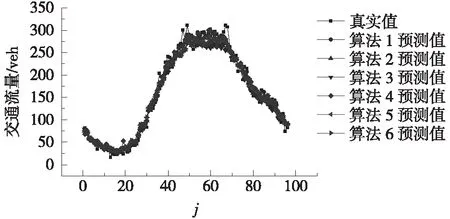
(c) p=96
5 结束语
1) 6种KNN算法的预测性能与状态向量长度密切相关,难以确定合适的p值让某种算法在所有评价指标上均表现最佳。
2) 对筛选出来的近邻进行PCA,可提取反映近邻主要变化趋势的主成分,有利于预测当前交通流的变化趋势。
3) KNN-PCA法的预测结果能很好地反映真实交通流的总体变化趋势,尤其在交通流量较大的时间段,预测值与真实值更为吻合。
4) 采用相关系数比采用欧式距离来筛选近邻更有利于保证KNN-PCA法的预测精度。此外,将1 d的数据长度作为KNN-PCA法的状态向量长度较为合适。
5) 提出的KNN-PCA法可用于高速公路的短时交通流预测,该方法原理清晰、计算简单、无需迭代。
