京津冀气象条件对学龄前儿童流感的影响及预报方法研究*
2022-07-08陈仲榆柳艳香鲁亮
李 怡 陈仲榆 柳艳香 鲁亮
1.中国气象局公共气象服务中心,北京,100081
2.中国疾病预防控制中心传染病预防控制所,北京,102206
1 引言
流行性感冒(以下简称流感)是一种严重危害人体健康的急性呼吸道传染病,通常在秋、冬季流行(Baumgartner,et al,2012)。中国流感呈多样化的季节性特征,A 型流感在北方省份呈冬季流行模式,位于热带的南方省份每年4—6 月流感流行,中纬度的省份流感呈每年1—2 月和6—8 月的双周期流行特点;B 型流感在中国大部分地区呈冬季高发型(Yu,et al,2013)。《中国流感疫苗预防接种技术指南》中指出,5 岁以下儿童、老年人、孕妇和慢性基础病患者等流感高危人群,患病后出现重症和死亡的风险高。季节性流感的负担并非按年龄平均分布,一项对全球季节性流感相关呼吸系统死亡率的研究(Iuliano,et al,2018)估计,全球92 个国家每年约有9243 至105690 名5 岁以下儿童死于流感相关呼吸道疾病。流感给儿童带来了巨大的疾病负担,尤其是在人口密集的地区流感更易发生交叉感染。因此,文中聚焦超大城市群—京津冀地区学龄前儿童流感开展研究。
以往研究(Polozov,et al,2008)表明,流感的传播与气象条件密切相关。从流感病毒结构特征来看,气温会改变流感病毒脂质包膜的形态,在较低的温度下,流感病毒脂质包膜为有序排列的固态,有利于维持病毒的完整和稳定,病毒更易被传播。气温、相对湿度常被认为是显著影响流感传播的气象因素(Li,et al,2018)。不同类型流感病毒流行峰值与气温暴露-反应关系不同,如甲型流感病毒分别在-4℃和28℃出现两个传播高峰,而乙型流感病毒通常在5℃达到高峰(Dai,et al,2018)。除了温、湿条件外,气压对流感发病也有重要贡献(Liu,et al,2019a)。值得注意的是,气象条件对流感的影响存在区域差异和协同效应,温带地区寒冷干燥和热带地区潮湿多雨与流感流行关系密切程度不同(郭倩等,2020)。上海在梅雨结束后的高温、高湿天气及冬末初春由于气温日较差较大会引起流感高发(陶芳芳等,2010)。在西南地区,较低的周平均温度和绝对湿度及无风的气象条件可持续4 周显著增加流感风险,较高的相对湿度也会持续3 周增加流感风险(Qi,et al,2021)。同时,流感发病对气象条件具有滞后性,研究(Liu,et al,2019b)指出最低温度每降低5℃,滞后1 周后流感病例数增加8%。
近年来,中外学者研发了多种流感预报方法。以统计模型最为常见,如采用累计和(Cumulative Sum Control Chart,CUSUM)模型开展流感流行起始时间预警(段玮等,2017),或采用支持向量机建立流感样病例预警模型(卢汉体等,2015)等。随着人工智能的不断发展,很多流感预报新方法不断涌现,如利用社交媒体中带有地理标记的流感相关关键词,通过多元线性回归、人工神经网络等方法建立实时预测模型(Lu,et al,2019;Wang,et al,2020)。但是,目前很少针对学龄前儿童这类敏感性人群开展流感与气象条件的关系和预报方法研究。学龄前儿童的免疫力相对较低,幼儿园人员密集,更容易感染流感,预防学龄前儿童流感传播也更为困难。因此,学龄前儿童流感发病与气象条件的关系更加值得关注,对学龄前儿童流感发病的预报也成为亟待研究的问题。
本研究基于流感病例资料,开展京津冀气象条件对学龄前儿童流感发病影响研究。在此基础上,基于机器学习方法建立该地区学龄前儿童发病人数预报模型,并进行历史回报检验,旨在为预防流感和行业服务提供科学依据。
2 数据与方法
2.1 数据
收集整理2014 年1月1日至2016 年12 月31日京津冀地区13 个地级市(直辖市)的流感日发病数资料,包括临床诊断病例和实验室确诊病例。资料来源于中国疾病预防控制中心疾病监测信息报告管理系统(数据已脱敏),涉及的信息包括性别、年龄和发病时间。选取学龄前儿童(6 月龄—6 岁龄)日发病数资料,用于气象条件与流感的暴露-反应关系分析和预报模型的构建。选取京津冀地区13 个国家级地面气象观测站对应时段内的逐日平均气温、相对湿度、降水量、本站气压、平均风速、日照时数。气象条件对人体健康的影响通常是多个要素相互影响、协同作用的结果。因此,除单一气象因素外,引入大气环境人体感知度(BPWI)这一综合气象指标(柳艳香等,2022),用于评价综合气象条件对学龄前儿童流感发病产生的影响。
2.2 方法
(1)广义相加模型(Generalized Additive Model,GAM)。流感日发病数近似服从泊松分布,GAM 的误差分布选用泊松分布作为模型的分布族,取对数连接函数。非参数函数的形式选用平滑样条法,采用平滑样条函数可以最大程度拟合气象因素与日发病数的关系(Liu,et al,2019b)。基本模型如下

式中,E(Yt)为观察日(t)流感病例期望值;α 为拟合常量;s(*)为惩罚样条函数,time 为时间,df 为自由度;Xt为观察日(t)的气象要素,X可取气温、相对湿度、气压和BPWI 等;DOW 用于控制星期效应。依据赤池信息准则(AIC)最小和残差最小的准则,调节各项自由度,作为最优模型。将时间自由度定为7,气象要素自由度定为4。相较严格线性模型而言,广义相加模型的优点在于存在连接函数和平滑函数,能较好地处理自变量和因变量间的非线性关系,且保留相加性质。这样能对各预报因子贡献度进行单独分析和比较,是一种能较好兼顾可解释性和灵活性的回归模型。
(2)XGBoost 机器学习预报方法
采用XGBoost(Extreme Gradient Boosting)机器学习方法建立京津冀地区学龄前儿童流感发病预报模型,并进行模拟效果检验。XGBoost 是梯度提升决策树集成算法的高效实现。梯度提升决策树通过决策树结构实现回归器叶节点的集合,算法具有较强的非线性拟合能力。XGBoost 在梯度提升决策树的基础框架上整合了多种目标函数、优化算法、树分列算法等参数选项,具有较好的数据自动识别预处理能力及计算性能(Chen,et al,2016)。
3 流感特征及其与气象条件关系分析
3.1 流感特征分析
收集到的2014—2016 年京津冀地区流感发病数共118636 人,其中学龄前儿童发病数26525 人。对京津冀地区流感发病总体特征分析发现,京津冀地区以北京流感发病率最高,3 a 的年平均发病率每百万人为597 人,而天津和河北的年平均发病率分别是每百万人149 人和36 人,可见人口密集地区和人口流动性高的地区,流感发病率相对较高。采用核密度估计(Kernel Density Estimation)方法,获得能够近似表示流感数据分布的密度函数每一点的估计值,从而得到2014—2016 年京津冀地区流感发病年龄分布情况(图1)。在京津冀地区各年龄段发病人数中,0—6 岁为流感发病人数的第一个峰值,也是最大值区间。京津冀学龄前儿童相较于其他年龄段人群更易发病属于流感的一个典型特征。中外相关研究也曾指出低龄儿童存在一个流感发病高峰,如天津市、南京市、福州市等流感样病例以低年龄组发病占比最高(李媛等,2011;于永等,2015;郑月燕等,2019)。芬兰、美国、澳大利亚等相继有研究(Silvennoinen,et al,2011;Worby,et al,2015;Huang,et al,2017)表明低龄儿童流感发病和住院率的相对风险最高。学龄前儿童流感高发的因素有多个方面,比如儿童年龄越小,体内的流感病毒抗体较其他年龄段的人群少,免疫力和对流感病毒的抵抗力差(秦强等,2019)。另外,由于流感病毒通过飞沫和受病毒污染的手传播,幼儿园的集体生活使得学龄前儿童相互间接触频繁,从而造成流感传播。

图1 京津冀流感发病年龄密度分布(a.2014 年,b.2015 年,c.2016 年)Fig.1 Kernel density estimates of age distribution of influenza occurrence in Beijing-Tianjin-Hebei area(a.2014,b.2015,c.2016)
流感一年四季都可能发生,且发病时间分布不均。从京津冀学龄前儿童流感逐月发病人数与月平均气温的时间序列(图2)分析,逐月学龄前儿童发病人数呈单谷型分布,12—3 月发病人数最多。4—7 月发病人数连续减少,7 月发病人数最少,之后发病人数逐月增多。发病人数在11、12 月之间增幅最大。月平均气温与流感发病人数呈反向变化,表现为单峰型分布。1 月的平均气温最低,10—12 月的平均气温降幅较大,以及2—3 月月平均气温波动较大,均对应着发病人数较多的月份。京津冀学龄前儿童流感在这些时期高发,主要是由于京津冀地区地处华北平原,冬、春季受西伯利亚高压和东北冷涡活动的影响,来自高纬度地区的强冷空气南下直达华北平原,导致该地区常出现寒潮和大风降温过程。当寒潮过境时,当地气压升高,往往伴随着剧烈降温,人体热平衡很难及时调节达到新的平衡态,从而导致人体免疫力下降,流感传播的可能性变大,尤其对于儿童更是如此。京津冀地区学龄前儿童发病的分布(图3)也印证了该地区学龄前儿童流感发病的高发时段为冬季,其次为春季和秋季。并且各季节也是北京的学龄前儿童发病率最高,其次是与北京毗邻的廊坊,河北省的衡水、秦皇岛也是发病率较高的城市。

图2 京津冀2014—2016 年学龄前儿童流感逐月发病人数与月平均气温时间序列Fig.2 Monthly time series of preschool children influenza cases and monthly average temperature in Beijing-Tianjin-Hebei area from 2014 to 2016

图3 京津冀学龄前儿童流感各季节日平均发病率特征(a.春季,b.夏季,c.秋季,d.冬季)Fig.3 Average daily incidence of influenza in preschool children in Beijing-Tianjin-Hebei area(a.spring,b.summer,c.autumn,d.winter)
3.2 气象因素基本情况
分析流感发病与气象条件的暴露-反应关系之前,首先分析影响学龄前儿童流感的气象条件是否存在共线性。采用斯皮尔曼(Spearman)相关计算京津冀逐日BPWI、气温、相对湿度、风速、日照时数、气压、降水量之间的相关系数(表1)。气温与BPWI 的相关系数r=0.993(P<0.001),两者之间存在显著的共线性。这是由于BPWI 采用气温、相对湿度、风速和日照时数4 个气象要素构建,且气温所占权重最大(约50%)。气温与BPWI 的这种显著相关也表明BPWI 能很好地反映气温的变化。另一组相关较高(相关系数|r|>0.6)的气象要素是气温与气压。冷空气过境,带来气压升高,气温降低,气温和气压虽然存在较高的相关,但由于两者的物理动力过程明确,不能简单的判别为存在共线性。其余气象要素间相关系数较小(|r|<0.6),不存在共线性。各气象要素统计值如表2 所示。其中,京津冀地区日平均气温2014—2016 年平均值为12.95℃,BPWI 的平均值为-2.95。BPWI 为负值,往往表示向冷变化;BPWI 为正值,则表示向暖变化。由于BPWI 综合了气温、相对湿度、风速及日照时数的协同作用,表征了人体对气象条件综合影响的感知程度。

表1 2014—2016 年逐日各气象要素间的相关系数Table 1 Correlation coefficients between daily meteorological factors from 2014 to 2016

表2 2014—2016 年逐日各气象要素区域平均统计量Table 2 Statistics of daily regional-mean of meteorological factors in Beijing-Tianjin-Hebei area from 2014 to 2016
3.3 流感发病与气象条件的关系分析
通过Spearman 相关分析得到了学龄前儿童流感发病当日和不同滞后天数的发病人数与各气象要素的相关系数(表3)。当相关系数|r|>0.3 且P<0.001 时,认为该气象要素与流感发病存在显著相关。就发病当日的情况而言,平均气温和BPWI对学龄前儿童发病人数影响显著,相关系数分别为-0.762 和-0.751(P<0.001),呈显著的负相关关系。这表明当气温下降,或BPWI 综合指数为负值时,学龄前儿童流感发病人数将增多。其次,相对湿度也与流感发病数呈显著负相关,相关系数为-0.381(P<0.001)。气压则与流感发病人数呈显著正相关关系,相关系数为0.534(P<0.001),表现为当地表气压增高,京津冀地区儿童流感发病增多。气温、气压和气象综合指标(BPWI)与流感发病人数的显著相关,说明当气象条件发生变化时,会对流感发病造成影响。具体而言,当冷高压过境时,带来北方冷空气和降温过程,京津冀地区儿童流感发病人数有明显增多趋势。此外,日照时数和降水量与流感发病的相关系数绝对值较小,表明两者对流感发病人数未造成显著影响。风速与流感发病的线性相关关系不显著(0.224<P<0.9778)。
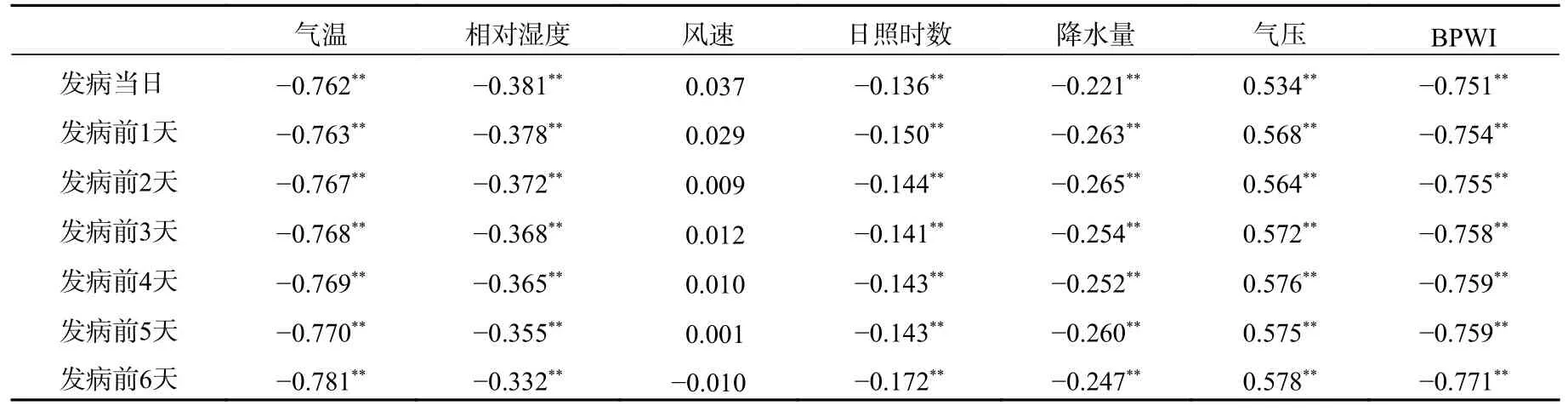
表3 2014—2016 年京津冀学龄前儿童流感发病与气象要素(发病当日及滞后)相关系数Table 3 Correlation coefficients between preschool children influenza cases and meteorological factors at the onset day and various lag days from 2014 to 2016
流感发病具有潜伏期,表现为流感发病对气象条件变化具有一定的滞后。京津冀学龄前儿童流感发病人数与发病前1—6 d 的气象要素间的滞后相关系数(表3)表明,流感发病与一周以内的气温、相对湿度、气压和BPWI 具有显著的相关关系(P<0.001)。一周以内,流感发病与前6 d 的气温、气压和BPWI 的滞后相关系数最大,与发病当日的相对湿度的相关性最大。而流感发病与降水量、平均风速、日照时数的滞后相关系数较小或不显著。
基于Spearman 相关分析得到显著影响流感发病的气象要素后,采用GAM 进一步分析流感发病与这些气象要素的非线性关系。为了避免气温与BPWI 共线性的影响,首先进行敏感性分析,设计单一要素(气温、相对湿度、气压)和综合气象条件(BPWI、气压)两种方案。遵循最小AIC 和残差的准则,综合气象条件方案对流感发病人数拟合更优。因此,分析BPWI 和气压与流感发病的暴露-反应关系,并应用于预报方法的研究。由BPWI 与学龄前儿童流感发病人数暴露-反应关系(图4a)可以看出,BPWI 与学龄前儿童流感发病人数存在非线性相关,BPWI 与流感发病的暴露-反应关系曲线存在1 个低值点,在该点两侧,BPWI 升高或者降低时,流感发病风险均增大,即得到最适BPWI 值为-11。当BPWI≤-11 时,随着BPWI 减小,流感发病风险增大。当-11<BPWI<0 时,随着BPWI 增大,流感发病风险增加。当0≤BPWI<10 时,随着BPWI 减小,流感发病风险增加。从BPWI 低于10 开始,这一综合气象条件就对流感发病产生影响,尤其当BPWI 低于最适值时,综合气象条件对流感发病的影响最大。分析发现,当BPWI 为-11 时,对应京津冀地区的气温约为4℃。气压与流感发病呈现出近似于线性相关的关系(图4b),当气压>905 hPa,气压对流感发病的影响呈正趋势,随着气压的升高,流感发病风险增大。当气压达到1007 hPa 时,此时流感发病风险最高,该气压为拐点气压。在此之后,气压与流感发病的关系曲线趋于平缓。BPWI 和气压与学龄前儿童流感发病的暴露-反应关系具有统计学意义(P<0.001)。

图4 2014—2016 年京津冀学龄前儿童流感发病人数与(a)BPWI 和(b)气压的关系(实线表示流感相对危险度(RR),虚线表示95%置信区间)Fig.4 Relationships of influenza cases with(a)BPWI and(b)station pressure among preschool children in Beijing-Tianjin-Hebei area during 2014—2016(the solid line represents the logarithm of the relative risk of influenza,the dotted line represents the 95% confidence interval)
4 预报方法研究
非线性回归结构的XGBoost 机器学习方法属于决策树算法。构造决策树首先需要合理划分数据集。为保持疾病数据的时间均匀和要素特性,利用随机采样方法分离训练集和检验集。训练集大小控制为总数据集的80%,总数据集的20%作为检验数据,检验数据集不参与模型训练,仅用于回报检验。
考虑流感发病对气象条件存在滞后性,将气象类预报因子(BPWI 和气压以及它们的超前量)和非气象类预报因子(日期)作为自变量,代入模型进行训练,得到学龄前儿童流感发病人数。为评估模型的性能,采用平均绝对误差、均方根误差、决定系数3 种评估指标。计算得到XGBoost 模型的平均绝对误差为5.766,均方根误差为9.635,决定系数为0.94。决定系数越大,误差越小,表明模型的模拟性能越稳定越好。对模型特征量进行重要性分析(图5),XGBoost 模型中,贡献度前五的特征量为超前3 天的BPWI、日期、超前5 天的BPWI、当天的BPWI、超前5 天的气压。其中,贡献大的特征量反映了超前3 天的BPWI 变化对流感发病具有显著的影响,其次为时间特征。各特征量重要性还反映出BPWI 对流感预报重要性高于气压。

图5 XGBoost 模型的特征重要性分析Fig.5 Analysis of feature importance of the XGBoost model
利用京津冀学龄前儿童流感发病历史人数进行回报检验,以评估模型的回报准确度和回报效果。为保证检验样本的独立性,使用随机采样得到的检验数据集进行检验,将模型历史回报得到的发病人数与检验集实际发病人数对比。分析流感模型的回报拟合度(图6),模型的历史回报值和检验集实际值在小值区的离散程度相对较小,回报值与实际值的吻合较好;在大值区,历史回报值更为发散。离散程度越大,拟合性能越差,历史回报值与实际值差距越大,模式回报效果越差。该模型得到的检验集历史回报值与检验集实际发病数拟合性高(决定系数为0.94)。对模型的历史回报效果进行检验(图7)发现,京津冀地区儿童历史回报值与检验集实际值的Spearman 相关系数达到0.892(P<0.001)。历史回报发病人数在冬春季峰值趋势和实际发病人数的趋势吻合度高,同时低值趋势吻合程度更好,预报模型能很好地捕捉流感高发日和低值日的特征。历史回报发病人数和实际发病人数相关性高,可见,使用XGBoost 构建的预报模型对京津冀地区学龄前儿童流感发病的预报较为可靠。
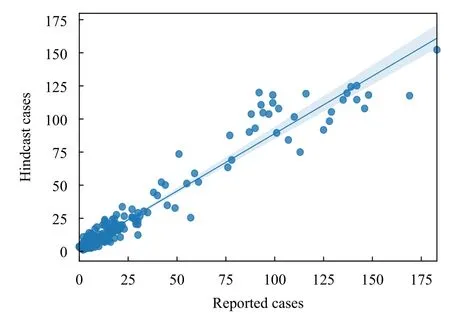
图6 京津冀学龄前儿童流感预报模型回报拟合度(横坐标为检验集实际发病人数,纵坐标为检验集回报发病人数,蓝实线为回报值与实际值的拟合线,阴影为95%置信区间)Fig.6 Degree of fitting for prediction of preschool children influenza cases by prediction model in Beijing-Tianjin-Hebei area(the horizontal axis is the reported cases in test set,the vertical axis is the hindcast cases in test set,the solid blue line is the fitting line between the hindcast value and the reported value,the shade is the confidence interval of 95%)

图7 京津冀学龄前儿童流感历史回报效果检验Fig.7 Validation of hindcast for preschool children influenza cases in Beijing-Tianjin-Hebei area
5 结论与讨论
利用京津冀地区学龄前儿童流感发病人数和气象观测资料,研究了该地区学龄前儿童流感发病人数与气象条件的关系,采用XGBoost 机器学习方法进行了预报试验,结果表明:
(1)一周以内的气温、相对湿度、气压和BPWI与流感发病人数存在显著线性相关。风速、日照时数、降水量与流感发病人数的线性相关系数较小或不显著。BPWI 与气温具有较强的共线性,相关系数达0.993,BPWI 能反映气温的变化特征,同时考虑了相对湿度、风速和日照时数的特征。BPWI 与流感发病人数的暴露-反应关系显著,最适BPWI 值为-11,对应气温约为4℃。当BPWI≤-11 或0≤BPWI<10 时,随着BPWI 减小,流感发病风险增大。当气压>905 hPa,随着气压的升高,流感发病风险增大。当气压达到1007 hPa 时,流感发病风险最高。天气过程中的各个气象要素并不是独立存在的,它们之间相互影响,这也是引入BPWI 这一综合气象条件指标并分析其对流感发病影响的重要原因。
(2)基于诱发京津冀学龄前儿童流感发病的气象条件—BPWI 和气压开展了XGBoost 机器学习方法的预报建模试验。预报模型中贡献度前五的特征量为超前3 天的BPWI、日期、超前5 天的BPWI、当天的BPWI、超前5 天的气压,尤其是超前3 天的BPWI 对流感发病具有明显的影响。模拟性能评估和历史回报检验的结果均表明模型对京津冀学龄前儿童流感发病预报具有较好的模拟性能和预报效果,可作为预报模型应用到实际预报中,以此为流感的分类人群干预提供预报依据。
需要说明的是,本研究建立的预报模型也可用于其他城市的流感预报建模,但不同地区的流感病毒类型和传播速率不同,因此各城市的流感预报模型应该纳入地理位置、社会人口等对流感传播存在潜在影响的要素。同时,尽管本研究得到了京津冀学龄前儿童流感发病与气象条件之间显著的相关关系和较好的预报试验效果,但是还有待于开展不同气候区各类敏感人群的流感疾病与气象条件的关系研究,以优化预报方法。
