三角高程测量单向观测中大气折光系数的取值探讨
2022-07-08张豫宁陈裕汉彭晨
张豫宁,陈裕汉,彭晨
(1.昆明理工大学国土资源工程学院,云南 昆明 650093; 2.滇西应用技术大学,云南 大理 671009;3.云南省测绘工程院,云南 昆明 650033)
1 引 言
我们知道,传统的三角高程测量采用对向观测的方法只能削弱但不能完全抵消大气折光的影响,因此观测结果依旧停留在三、四等水准测量的精度,大气垂直折光的影响也成为制约三角高程测量精度的因素之一。在仪器和观测者不变的条件下,三角高程测量观测精度主要取决于实地大气折光的影响[1],根据球气差改正公式可知,当区域的大气折光系数K值确定了,球气差改正值也更接近于真值,改正后三角高程测量单向观测的精度也更高[2]。本文以大理滇西应用技术大学的控制测量数据为主,计算出实际的K值,并分析在不同K值下球气差对高差改正的精度影响。
2 大气折光系数的取值及计算方法
下列将以三种不同的方法来获得大气折光系数K值,其中经验值法可根据文献资料直接取值;而另外的两种方法则需要先确定球气差系数C值,再通过计算公式来反推出K值。球气差系数C值与大气折光系数K值的推导公式如下:
(1)
K=1-2R·C
(2)
式中R为测区的平均曲率半径,和测区所在的纬度有关,R取 6 366 787 m。
2.1 大气折光系数经验值的取值范围
由于自然环境因素的影响,不同区域的K值也不尽相同,根据对以往大量的测量数据计算分析,大气折光系数经验值的取值范围在0.07~0.16之间[3],如表1所示。

不同区域经验K值的取值范围 表1
在实际三角高程测量工作中,通常采用对向观测的方法来削弱大气折光的影响,计算时采用的经验K值是一样的,因此通常使用该观测方法来“抵消”大气折光的影响[4];而在进行单向观测时,由于测量精度的要求不高,球气差改正常用经验K值参与计算或者不做改正。但在条件允许的情况下,不能仅依赖于用经验K值来代替实际的K值,还是需要通过一些实测数据推算取平均值后得到的K值才可靠[5],这样也可以为该区域提供一个重要的测量参数[6]。
2.2结合精密水准求定K值[7]
因为几何水准测量是目前精度最高的高差测量方法,所以可将水准测量往返测高差中值当作测段高差的真值来使用,再对测段进行三角高程联测,用两者所测得的高差计算K值,该方法可以计算出同一个测段往测和返测两个方向的K值,但测段最后的K值结果需要取平均值,具体计算公式如下:(本文中D为平距)
h水准=h三角高程+CD2
(3)
(4)
(5)

(6)
2.3 往返观测高差与单向测量高差比较来求定K值[7]
该方法利用三角高程测量往返测高差作为计算数据,假设测量是在等精度观测下完成的,那么就可以认为往返观测的大气折光系数是一样的,但结合实际工作环境,这样完全理想的条件是难以达到的。通过往返测高差不符值的平均值来求解K值,此方法可以直接计算出一个测段的K值,具体公式如下:
h往+h返=-2CD2
(7)
(8)
(9)

(10)
以上三种方式是常见的K值的取值和计算方法,实验将逐一展开计算和研究;本次实验场地表覆盖情况状况基本一致、两点之间植被基本均一,形状基本对称,观测条件较理想;因观测边较短,故不考虑垂线偏差的影响[8]。
3 实验研究
3.1 大气折光系数计算
本次实验用到的仪器分别为拓普康GM-52和科力达DL-2007数字水准仪,由于仪器设备及观测要求的限制,高程导线高差精度达到四等,几何水准测量精度达到三等。根据大气垂直折光向下弯曲的原理,三角高程高差必须比水准测量高差小,因此三角高程高差与三等水准高差之差必须为负值,正值为异常边,则必须将正值的测段剔除。实验共计观测了16条边,其中6条为异常边,某些异常边的单向观测可用于检核计算,剩下10条为合格边参与K值计算[9]。利用上述2.2和2.3两种方法对区域内的大气折光系数进行计算,如表2所示。
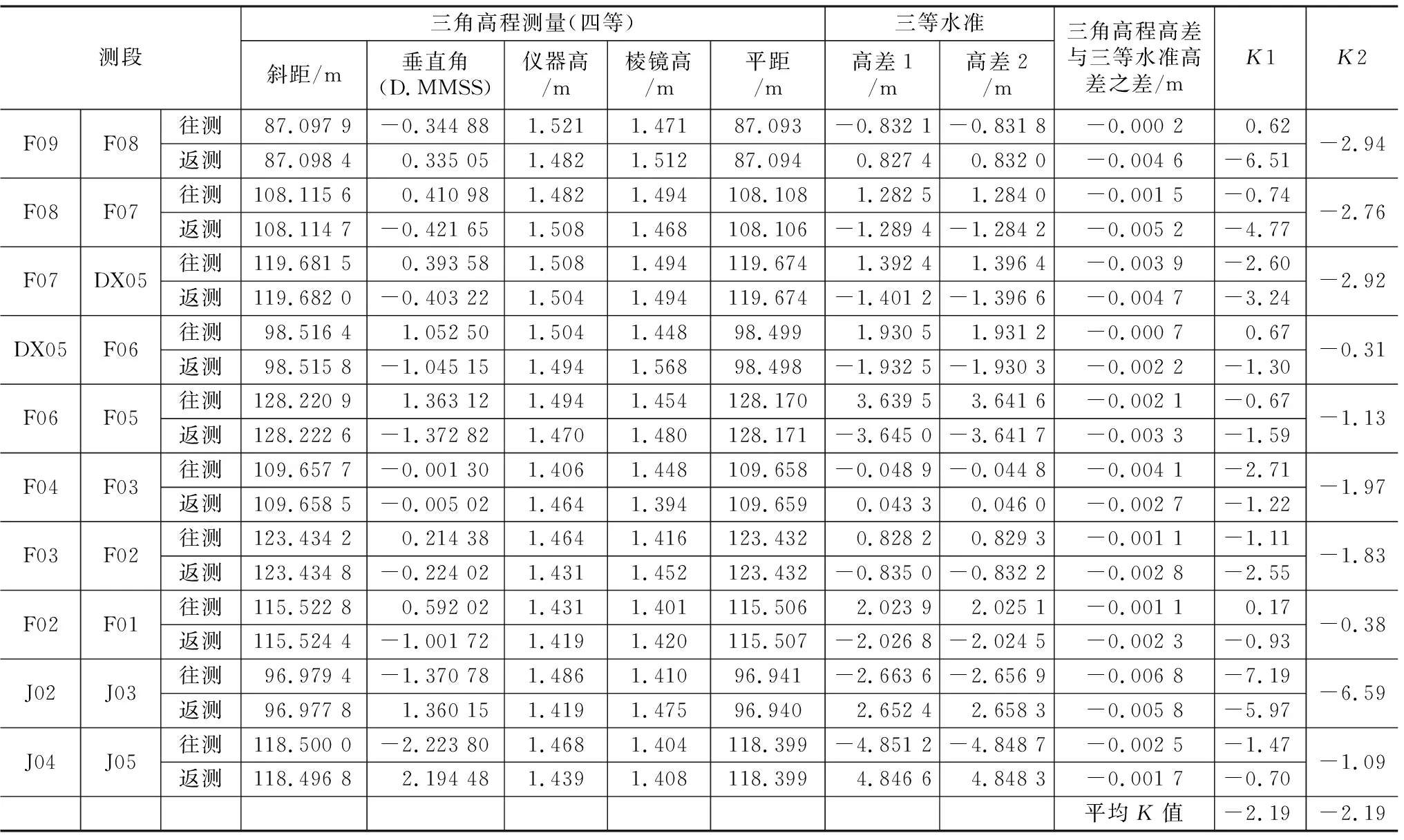
实验数据计算 表2
表2中各测段K1的平均值等于K2的值,通过两种方法计算得到的平均K值是一样的,最终以-2.19作为本次实验区域的K值参数无误。
3.2球气差改正计算及对比
本小结选择满足条件的6条异常边作为球气差改正的检核边,选择经验K值0.13和和计算值-2.19进行球气差改正计算及高差对比,如表3、表4所示:

球气差改正计算 表3

球气差改正后高差精度对比 表4
利用计算的K值对三角高程高差进行球气差改正后,理论上改正后的高差会更加贴近于三等水准高差的中值,但由于各测段上求解的K值存在一些差异,所以对某些测站上的改正效果还是会不太理想,但相比于用经验值0.13改正总体效果较好,测段高差精度得到改善,球气差改正后高差中误差减小,如图1所示。
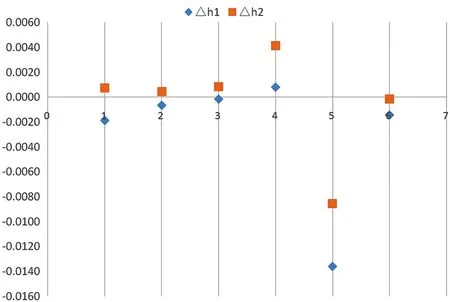
图1 高差精度误差分布
4 结 论
(1)实际工作中不能将大气折光系数作为一个常量系数来看待,作为一个测量参数更适当;通过测量数据计算出来的K值与经验K值会存在很大差异,且对球气差的改正值影响较大。
(2)使用以上两种反演方法计算得到的平均K值一样,说明了计算公式的严密性,且两种计算方法具有联系性;无论采用哪一种方法计算来区域的实际K值,都必须使用完整的测段数据。
(3)在距离不变的情况下,K值趋向于负递减时,球气差改正越大;K值趋近于1时,球气差改正值就越小。
(4)在实际进行三角高程测量单向观测时,在条件允许的情况下建议使用计算出来的K值对测段高差进行改正,尽可能提高观测精度。
(5)由于条件限制,区域内的测量数据较少,本文计算得到的实际K值不具有代表性,但结合测量数据验证了两种K值反演方法的联系性,对今后K值反演数据的测量要求提供了帮助;本文只是对实际生产工作中K值的取值方法做一个探讨性的研究,该地更严密的K值还需后续大量的测量资料汇总计算得到。
(6)目前在三角高程测量外业观测中,采用对向观测的方式是削弱大气垂直折光影响最有效的途径。
