非对称锚定面内开关液晶平板光波导的色散方程

2022-07-07查正桃张谦述温倩周琪张耀进张冲董帅蒋勇

液晶与显示 2022年7期

查正桃张谦述*温倩周琪张耀进张冲董帅蒋勇

查正桃1，2，张谦述2*，温倩2，周琪2，张耀进2，张冲2，董帅2，蒋勇2

（1.西华师范大学物理与天文学院，四川南充 637009；2.西华师范大学电子信息工程学院，四川南充 637009）

为了准确计算液晶光波导中的模式，推导出了非对称锚定面内开关平板液晶光波导中横电模式的色散方程。进行了模式的求解，并与仅适用于均匀各向同性材料的传统色散方程得出的结果进行了比较。结果显示，传统色散方程得出的每一个模式的有效折射率都比本文方程的求解结果更大，且该偏差随模式阶数的增加而变得更加严重。在本文的例子中，基模、阶模、2阶模对应的最大偏差分别占液晶双折射的7.8%，17.8%，26.3%，这表明液晶指向矢的渐变特性对有效折射率解有不容忽视的影响。因此，相较于传统色散方程的不足，本文提出的色散方程能更有效地分析液晶光波导中的模式。最后，通过与已有的数值结果进行比较验证了本文提出的色散方程的有效性与准确性。

非对称锚定；面内开关；液晶；光波导；色散方程

1 引言

向列相液晶（Nematic Liquid Crystal， NLC）的大电光效应［1］和高光学双折射［2］使其能在低电压下电调谐液晶光波导的传播特性，而且其具有响应速度快［3］、在可见光与近红外波段的透光率高［4］等优势。目前，NLC已成为光子学领域中一种极具应用潜力的电光材料。近年来，基于非对称锚定面内开关（In-Plane Switching， IPS）模式的NLC平板光波导因其可近似产生纯横电（Transverse Electric， TE）和横磁（Transverse Magnetic， TM）模式，而逐渐引起了研究人员的兴趣，环形谐振器［5］、光学滤波器［6］、光开关［7］等基于IPS-NLC光波导的光学器件被相继报道。

在以上的研究中，NLC光波导的本征模式分析是最重要的步骤［8］，有效折射率计算的准确性直接影响到其器件的性能。实际运用中的液晶光波导通常具有锚定取向层［9］，由Freedericksz转变［10］可知当液晶指向矢在外加电压下发生场致重新取向时，其偏转角是沿外加电场方向逐渐变化的，从而产生在空间上渐变的液晶介电张量。因此，并不能直接应用有限差分法［11］、有限元法［12］、变分法［13］以及矢量伪谱法［14］等仅适用于均匀各向异性光波导的数值算法来分析IPS-NLC光波导的本征模式。这种IPS-NLC平板光波导的TM模式与液晶指向矢的偏转角无关，但其TE模式却受指向矢偏转角的调控。因此，传统的色散方程［15］也仅适用于计算IPS-NLC光波导的TM模式，却并不能准确分析其TE模式。文献［6］分析了一些特定电压下E7 （Merck）液晶的折射率拟合曲线，进而计算出IPS-NLC平板光波导中TE模式的有效折射率。但其结果是基于具体材料和特定电压所得出的，不仅不具有一般性，而且其折射率拟合函数中的系数复杂且难以确定。截至目前，正因为缺乏IPS-NLC光波导TE模式的色散方程，导致很难分析液晶指向矢的渐变特性对其有效折射率的影响，这在一定程度上也限制了能适用于不同外加电压的单模液晶光波导的准确设计。因此，为了能够准确分析任意外加电压下IPS-NLC平板光波导的本征模式，深化其应用，需要探索出其TE模式的色散方程。

本文基于麦克斯韦方程组，采用WKB法［16］的研究思路推导出非对称锚定IPS-NLC平板光波导中TE模式的模场分布和色散方程。然后，在给定的实例下进行模式的求解，通过与使用传统色散［15］方程得出的结果进行比较从而分析了液晶指向矢的渐变特性对有效折射率解的影响。最后，与之前已有的结果［6］进行比较，验证了本文提出的色散方程的有效性与准确性。

2 色散方程原理

式中，U为外加电压，为阈值电压，为Frank扭曲弹性常数，为真空中介电常数，为液晶的介电各向异性。此外，为液晶指向矢的最大偏转角，其值可通过令式（1）中得到。采用旋转矩阵［10］可得波导坐标系xyz下NLC的介电张量为

式中：

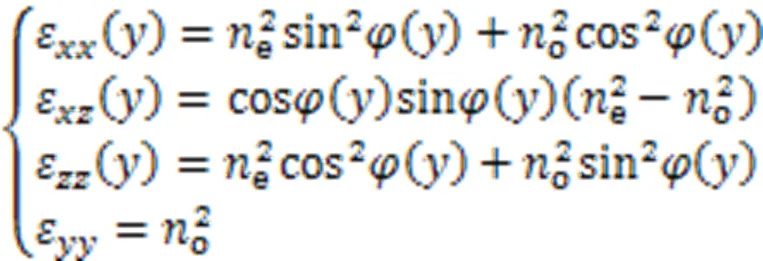
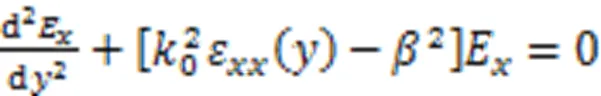
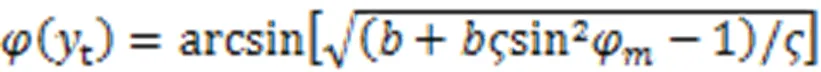
根据电磁分量在=0的边界条件［16］可得TE模式的色散方程为

3 实例与分析

为了与已有的结果进行比较，本文仍然选择典型的NLC E7 （Merck）作为波导材料，包层与衬底层均为熔融石英玻璃。IPS-NLC平板光波导的主要参数见表1。

表1IPS-NLC平板光波导的主要参数

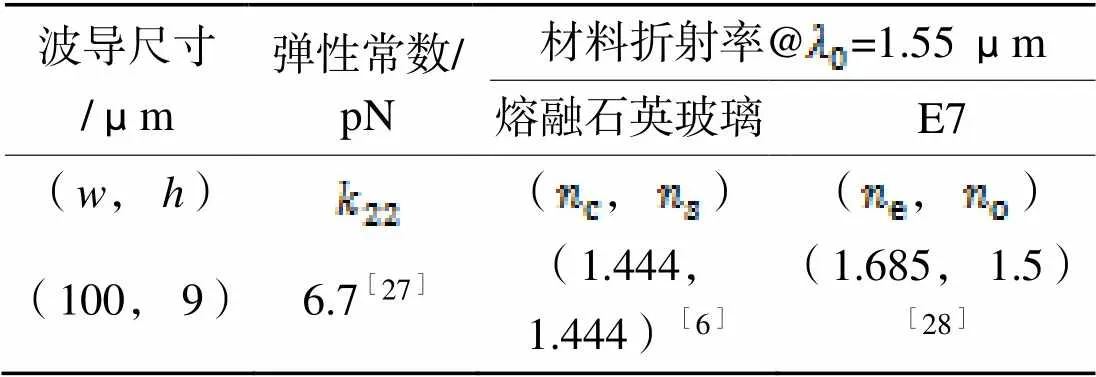
Tab.1　Major parameters of IPS-NLC slab optical waveguide

3.1　求解与讨论

图2　E7关键参数的电调谐特性。（a）介电分量；（b）折射率分布函数。

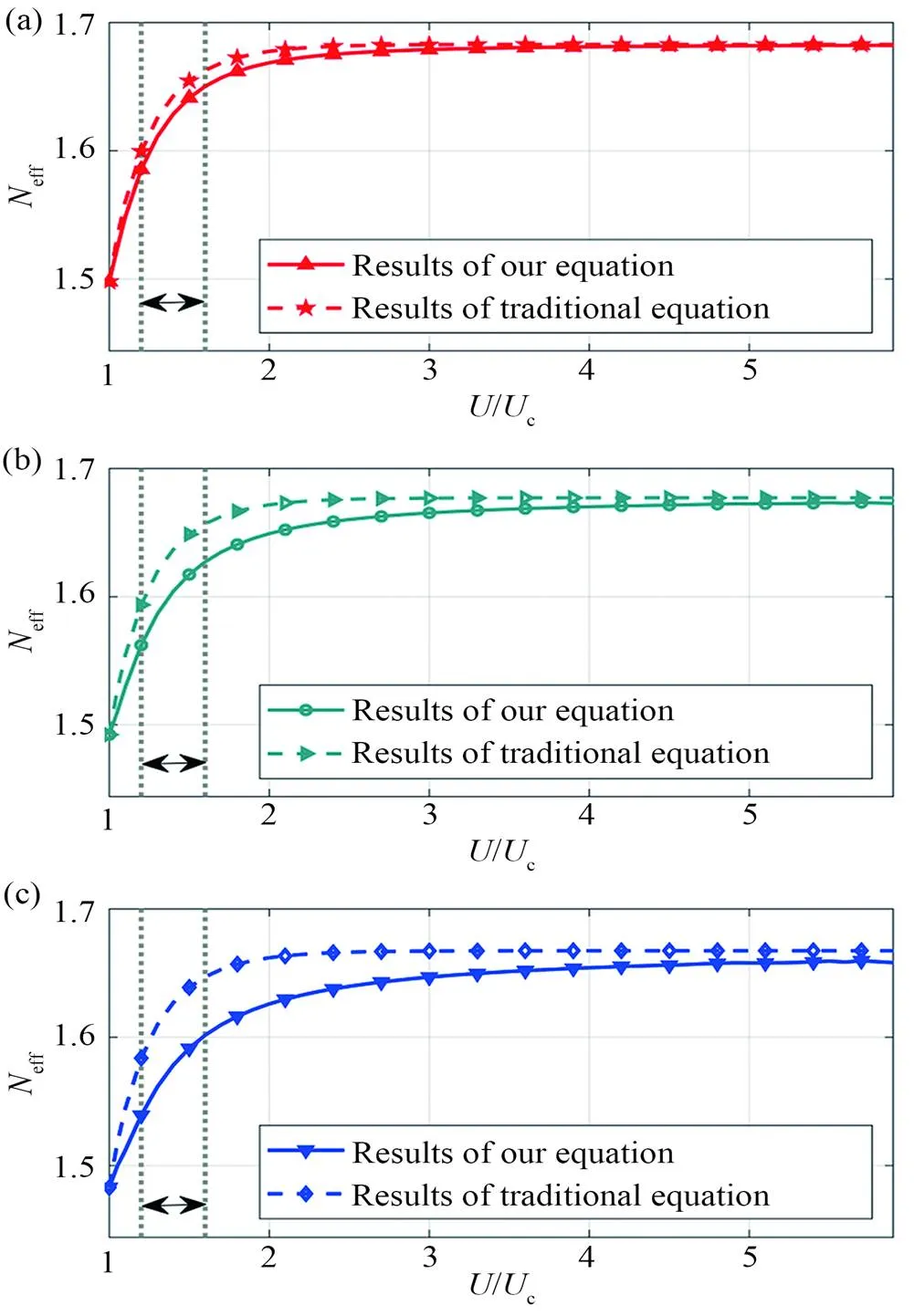
图3　有效折射率随外加电压的变化曲线。（a）基模；（b）1阶模；（c） 2阶模。

从图3可见，对于波导中的每一个模式，由传统方程得出的有效折射率总是比方程（10）求解出的结果更大。具体原因如下：

当外加电压略高于阈值电压时，由于几乎所有液晶指向矢的偏转角度是一致的，液晶的折射率分布函数衰减趋势平缓（图2（b）），此时非对称锚定IPS-NLC平板光波导可以被视为均匀各向异性光波导，从而两种方程得出的有效折射率间的差异较小。

随着外加电压的继续增加且位于图3中灰色虚线区间内时，各液晶分子偏转角度不一致的趋势逐渐明显（即不能达到最大偏转角的液晶分子数量开始增加），具体表现为液晶的折射率分布函数衰减趋势逐渐变得陡峭（图2（b）），从而导致两种方程得出的有效折射率间的差异逐渐增大。从图3中还可以看到，由两种色散方程得出的有效折射率之间的差异会随模式阶数的增大而变得更加严重。这是因为在同一外加电压下，液晶分子偏转角的梯度会随着转折点向波导上包层移动而增加。此外，当外加电压增加到某个特定值时具有最大的有效折射率偏差。在这里，基模、1阶模、2阶模这3个低阶模式所对应的最大有效折射率偏差分别占液晶双折射的7.8%， 17.8%， 26.3%，这个特定电压值介于1.3～1.4倍阈值电压范围内。

当外加电压超过这一特定电压值后，两种色散方程得出的有效折射率间的差异随外加电压的持续增加而逐渐减小，并在足够大的外加电压下，这种差异将趋于零。这是因为此时液晶指向矢偏转角度的渐变随外加电压的持续增加开始一直呈减弱趋势，并且在足够大的电压下IPS-NLC平板光波导可再次被视为均匀各向异性光波导。这一点可从图2（b）中液晶的折射率分布函数随着外加电压的增加而再次宽范围地趋于平缓得到证实。

基于以上结果可以得出，液晶指向矢的渐变特性在有效折射率解上存在不可忽视的影响。因此，用传统色散方程分析IPS-NLC平板光波导的TE模式是有所不足的，本文提出的色散方程能更准确地计算这种液晶光波导中的模式。

3.2　色散方程的有效性与准确性

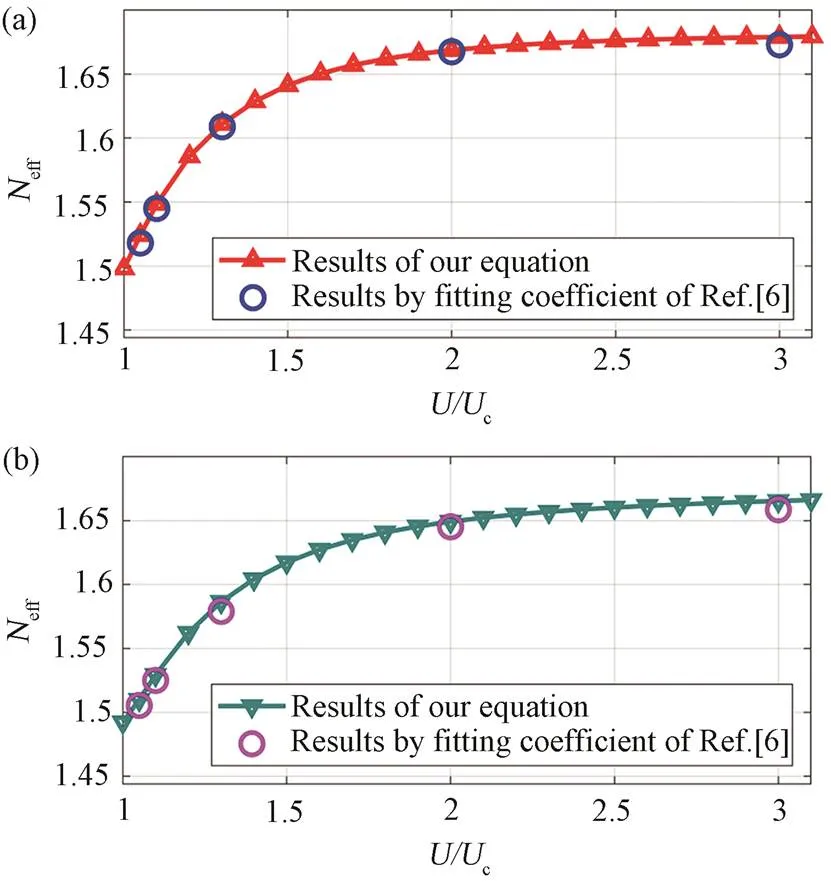
为了验证本文提出的色散方程的有效性与准确性，使用文献［6］中的拟合系数得出的数值结果与方程（10）的求解结果进行比较，如图4所示。

从图4可以明显看到，由色散方程（10）计算出的有效折射率与精确数值结果非常吻合，表明本文所提出的色散方程是有效及准确的。应当说明的是，因为文献［6］仅分析了几个特定电压下的折射率拟合曲线，所以这里仅含这些电压下的折射率值，但这仍能为本文所推导出的色散方程的准确性提供很好的验证。

4 结论

本文在考虑了液晶场致重新取向渐变特性的情形下，提出了一个适用于非对称锚定IPS-NLC平板光波导的色散方程。求解结果表明，该方程相较于传统色散方程能更准确地分析液晶光波导的TE模式。通过与之前的结果进行比较，验证了本文提出的色散方程的有效性与准确性。该色散方程能为基于IPS-NLC光波导的研究提供很好的帮助，例如，单模NLC光波导的设计以及光学相位延迟的准确测量。

［1］ KHOO I C， WU S T.［M］. Singapore： World Scientific Publishing， 1993.

［2］ DAVIS S R， ROMMEL S D， FARCA G，. A new electro-optic waveguide architecture and the unprecedented devices it enables［C］//6975，Ⅳ. Orlando： SPIE， 2008： 697503.

［3］ SHENOY M R， SHARMA M， SINHA A. An electrically controlled nematic liquid crystal core waveguide with a low switching threshold［J］.， 2015， 33（10）： 1948-1953.

［4］ BEECKMAN J， NEYTS K， VANBRABANT P J M. Liquid-crystal photonic applications［J］.， 2011， 50（8）： 081202.

［5］ DE CORT W， BEECKMAN J， JAMES R，. Tuning silicon-on-insulator ring resonators with in-plane switching liquid crystals［J］.B， 2011， 28（1）： 79-85.

［6］ TRIPATHI U S， RASTOGI V. Liquid crystal based rib waveguide［J］.， 2020， 38（15）： 4045-4051.

［7］ TRIPATHI U S， BIJALWAN A， RASTOGI V. Rib waveguide based liquid crystal EO switch［J］.， 2020， 32（23）： 1453-1456.

［8］查正桃，张谦述.液晶光波导中本征模内场分量间的关系［J］.液晶与显示，2022，37（1）：14-20.

ZHA Z T， ZHANG Q S. Relationship of field components in the liquid crystal optical waveguide eigenmode［J］.， 2022， 37（1）： 14-20. （in Chinese）

［9］查正桃，张谦述.基于液晶光波导的电控偏振旋转器［J］.中国光学， 2022， 15（3）： 552-561.

ZHA Z T， ZHANG Q S. Electrically controlled polarization rotator based on liquid crystal optical waveguide［J］.， 2022， 15（3）： 552-561. （in Chinese）

［10］ YANG D K， WU S T.［M］. ‍Hoboken： John Wiley & Sons Inc.， 2006.

［11］ FALLAHKHAIR A B， LI K S， MURPHY T E. Vector finite difference modesolver for anisotropic dielectric waveguides［J］.， 2008， 26（11）： 1423-1431.

［12］ LIU N， CAI G X， ZHU C H，. The mixed finite-element method with mass lumping for computing optical waveguide modes［J］.， 2016， 22（2）： 187-195.

［13］ OHTAKA M， KOBAYASHI T. Vector variational analysis of the guided modes in the three-dimensional anisotropic optical waveguides［J］.（：）， 1986， 69（8）：1-10.

［14］ HUANG C C. Modeling mode characteristics of transverse anisotropic waveguides using a vector pseudospectral approach［J］.， 2010， 18（25）： 26583-26599.

［15］ KAWANO K， KITOH T.：［M］. New York： John Wiley & Sons， Inc.， 2001.

［16］ CHEN C L.-［M］. Hoboken： John Wiley & Sons Inc.， 2007.

［17］ PERIVOLARI E， D’ALESSANDRO G， APOSTOLOPOULOS V，. Two-dimensional snapshot measurement of surface variation of anchoring in liquid crystal cells［J］.， 2021， 48（15）： 2086-2096.

［18］ CHOI Y， OH S W， CHOI T H，. Liquid crystal cell asymmetrically anchored for high transmittance and triggered with a vertical field for fast switching［J］.， 2020， 28（14）： 20553-20562.

［19］ CHEN H W， HUANG Y G， GOU F W，. New nematic LCD with submillisecond response time［J］.， 2018， 49（1）： 1691-1694.

［20］ NIE X Y， LU R B， XIANYU H Q，. Anchoring energy and cell gap effects on liquid crystal response time［J］.， 2007， 101（10）： 103110.

［21］ SUN Y B， MA H M， ZHANG Z D. Grey behaviour analysis of in-plane switching mode liquid crystal displays with weak-anchoring effects［J］.， 2002， 29（8）： 1059-1062.

［22］ SATO O，IWATA N， KAWAMURA J，. An in-plane switching liquid crystal cell with weakly anchored liquid crystals on the electrode substrate［J］.， 2017， 5（18）： 4384-4387.

［23］ KHOO I C.［M］. New York： Wiley， 2007.

［24］ AGRAWAL O P. Formulation of Euler-Lagrange equations for fractional variational problems［J］.， 2002， 272（1）： 368-379.

［25］ GRADSHTEYN I S， RYZHIK I M.，，［M］. 7th ed. Burlington： Academic Press， 2007.

［26］ HOCKER G， BURNS W. Modes in diffused optical waveguides of arbitrary index profile［J］.， 1975， 11（6）： 270-276.

［27］ YE W J， LI Z J， YUAN R，. Accurate measurement of the twist elastic constant of liquid crystal by using capacitance method［J］.， 2019， 46（3）： 349-355.

［28］ LI J， WU S T， BRUGIONI S，. Infrared refractive indices of liquid crystals［J］.， 2005， 97（7）： 073501.

Dispersion equation of asymmetric anchored in-plane switching liquid crystal slab optical waveguide

ZHA Zheng-tao1，2，ZHANG Qian-shu2*，WEN Qian2，ZHOU Qi2，ZHANG Yao-jin2，ZHANG Chong2，DONG Shuai2，JIANG Yong2

（1，，637009，；2，，637009，）

To calculate the modes in liquid crystal optical waveguides， we derive the dispersion equation of transverse electric （TE） mode in the asymmetrical anchoring in-plane switching nematic liquid crystal （IPS-NLC） slab optical waveguide by using the analytical thinking of the WKB method. The mode is solved and compared with the results obtained from the traditional dispersion equation. The results show that the effective refractive index of each mode obtained by the traditional dispersion equation is always greater than that calculated by our equation. The deviation between the effective refractive index is not only related to the applied voltage but also becomes more severe with the increase of the mode order. In the current example， the maximum deviations corresponding to the fundamental， first-order， and second-order modes account for 7.8%， 17.8%， and 26.3% of the liquid crystal’s birefringence， respectively. This result indicates that the gradient characteristic of the liquid crystal’s director has a non-negligible effect on calculating the effective refractive index. Consequently， the dispersion equation proposed by us can analyze the modes in the IPS-NLC optical waveguide more effectively than the traditional dispersion equation. Finally， the accuracy of the dispersion equation presented in this study is verified by comparing ours with the existing numerical results.

asymmetric anchored； in-plane switching； liquid crystal； optical waveguide； dispersion equation

O753+.2；TN252

10.37188/CJLCD.2022-0091

1007-2780（2022）07-0832-08

2022-03-21；

2022-03-31.

四川省科技厅科研基金（No.2014JY0024）；南充市科技局科研基金（No.19YFZJ0090）；西华师范大学英才科研基金（No.17YC056）

Supported by Scientific Research Foundation of Science and Technology Department of Sichuan Province （No.2014JY0024）； Scientific Research Foundation of the Science and Technology Bureau of Nanchong （No.19YFZJ0090）； Talent Scientific Research Foundation of China West Normal University Foundation （No.17YC056）

，E-mail：jackyzhang@cwnu.edu.cn

查正桃（1997—），男，四川自贡人，硕士研究生，2020年于西华师范大学获得学士学位，主要从事波导光学的理论与技术的研究。E-mail：zaktao@sina.cn