简化频域Volterra级数的S模式信号接收系统特性
2022-07-07宫峰勋李建坤
宫峰勋,李建坤
研究与开发
简化频域Volterra级数的S模式信号接收系统特性
宫峰勋,李建坤
(中国民航大学,天津 300300)
采用简化频域Volterra级数研究分析输入信号为S模式应答脉冲的多点定位(multilateration,MLAT)系统的非线性特性。首先以典型超外差接收系统为例,探索建立多点定位系统的简化频域Volterra级数模型和误差率模型;其次,研究建立基于核函数的S模式应答脉冲信号模型;最后分析输入基于核函数的S模式信号时,简化频域Volterra级数的S模式信号接收系统模型误差率。仿真结果表明,当输入基于核函数的S模式信号时,信噪比为15 dB的简化频域Volterra级数的接收系统模型误差率最小在23.23%以下;输入信噪比为16.25 dB的实际S模式测试信号时,该模型误差率最小在22%以下,小于误差率阈值。说明简化频域Volterra级数的接收系统模型可以准确地描述S模式信号接收系统的输出特性,为多点定位系统前导脉冲到达时间戳的识别奠定理论基础。
简化频域Volterra级数;S模式信号;非线性系统;核函数
0 引言
实际工程中的系统大多是非线性系统。对于弱非线性系统,可以使用线性系统近似代替。当系统越来越复杂时,线性系统已经无法满足实际要求,所以非线性系统逐渐成为人们的研究重点。文献[1]使用轨迹相平面法分析逻辑控制系统的特性,但该方法不适合分析弱非线性系统;文献[2]使用多特征卷积神经网络模型提取运动想象信号,但过程较复杂;文献[3-5]使用简化的Volterra级数模型分析非线性系统特性,但只局限于低阶Volterra级数模型;文献[6]使用Volterra级数推导射频功率放大器的输出交调失真方程,但并未获得 Volterra级数的显示表示式;文献[7]使用简化的频域Volterra级数模型分析电压互感器的输出特性,但对输入信号形式有严格限制;文献[8]使用三维频率空间的Volterra级数模型对发射机系统进行预失真处理,但并未绘制Volterra核的具体路径。
以S模式应答脉冲为输入信号的多点定位系统属于非线性系统。目前,对于此类系统的研究主要为内部非线性器件。文献[9]使用补偿记忆多项式模型提升功率放大器的线性度;文献[10]对接收机的非线性模块和记忆模块分别进行建模,但过程比较复杂;文献[11]使用基带Volterra级数分析接收机放大器的交叉信道非线性失真,但并未实际测试。

图1 超外差接收机的基站原理结构及S模式信号[12]
本文对基于简化频域Volterra级数的S模式信号多点定位系统特性进行研究。当输入基于核函数(kernel function)的S模式信号时,分析不同信噪比的简化频域Volterra级数的S模式信号接收系统模型误差率,并使用实际S模式测试信号加以验证。
1 简化频域Volterra级数的多点定位系统模型
1.1 超外差接收机结构及S模式信号
民航机场场面目标监视采用由多个基站组成的多点定位系统,该系统的基站属于超外差接收机。超外差接收机的基站原理结构及S模式信号如图1所示[12]。
超外差接收机基站工作原理是利用功率放大器、混频器、解调器等非线性器件将接收到的射频信号转换为基带信号,非线性特性主要来自内部的功率放大器、混频器等。此外,信号在传输过程中受到信道衰落、射频损伤、噪声等因素的影响[13],会使接收机出现谐波失真、互调失真[14]等现象。
1.2 简化频域Volterra级数的多点定位系统模型
Volterra级数可以分析非线性系统的输出特性,考虑核函数的对称形式,完整形式的频域Volterra级数表示式为[7]:
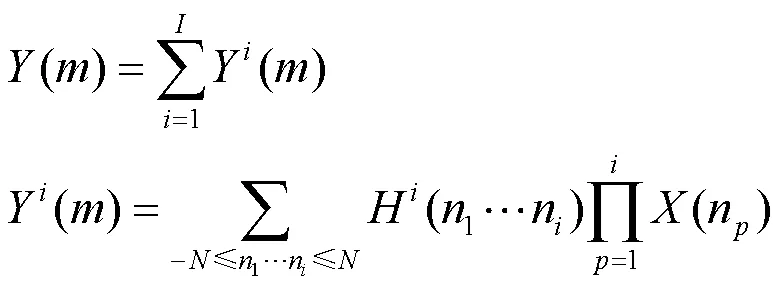
其中,和分别表示输入、输出信号的频谱,和分别表示输入、输出信号的谐波次数,表示系统的最高阶数,表示输入信号的最高谐波次数,表示系统的Volterra核函数,表示系统阶数,取值范围是1~,n表示输入信号的第次谐波,表示取值范围是1~的整数,n表示输入信号的第次谐波。完整形式Volterra级数计算量大,现对式(1)进行化简。假设输入信号为准正弦信号,该信号是含有多次谐波的周期性信号,且基波项幅值远大于谐波项幅值。在求解第阶系统的输出信号时,可利用输入信号的i个基波项(1)、i个基波共轭项(−1)及一个通用谐波项()的幅值乘积代替输入信号,并使用互调矩阵表示。其中p、i为非负整数,分别表示(1)、(−1)的数量。中的某一项元素为:

第阶系统下第次输出谐波()可用与表示[15]:

p、i有多组取值,每一组取值都对应一个核函数元素(p,i,)。则第阶系统下第次输出谐波的核函数矩阵为:

简化频域Volterra级数在描述系统输出特性时存在一定误差,使用式(5)表示简化频域Volterra级数的系统模型误差率:

其中,I()表示简化频域Volterra级数的非线性系统模型输出信号第次谐波项幅值,Iact()表示非线性系统输出信号第次谐波项幅值。为研究简化频域Volterra级数的系统模型误差率,设误差率阈值为30%,当TVE()<30%时,表示简化频域Volterra级数的系统模型误差率较小,可以准确描述系统的输出特性;当TVE()>30%时,表示该简化模型的误差率较大,不能准确描述系统的输出特性。
简化频域Volterra级数是Volterra级数的一种化简形式,因此可以描述非线性系统的输出特性。对于多点定位系统的S模式信号接收机,在已知输入输出信号的前提下反推出Volterra核函数,通过Volterra核函数可以构建基于简化频域Volterra级数的多点定位系统模型。
1.3 仿真结果及分析
分析一阶至十阶简化频域Volterra级数的多点定位系统模型误差率。系统阶数=10,所以=55,要求输入信号的数量≥55。设依次输入55个幅值不同的准正弦信号,每个输入信号中均含有直流项、基波项至九次谐波项,计算式为:
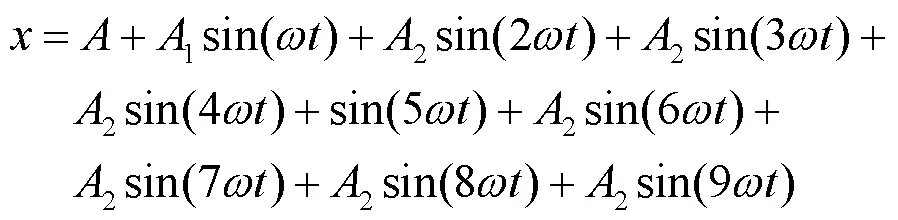
令直流项幅值=35 mV,基波项幅值1的取值范围是0.4~22 mV,间隔是0.4 mV;谐波项幅值均为2,取值范围是0.004~0.22 mV,间隔是0.004 mV;基波频率是50 Hz,相位为0。55个幅值不同的输入信号依次经过接收机系统后得到55个输出信号,由输入及输出信号反推出Volterra核函数。为求解简化频域Volterra级数的多点定位系统模型误差率,设待验证信号是,计算式为:

一阶至十阶简化频域Volterra级数的多点定位系统模型误差率仿真结果如图2所示。

图2 一阶至十阶简化频域Volterra级数的多点定位系统模型误差率仿真结果
由图2可知,七阶至十阶简化频域Volterra级数的多点定位系统模型中,第五次谐波误差率分别为14.2%、3.81%、3.960 5×104%、1.147 47×105%,明显高于其他谐波项。直流项误差率最大约为10.44%,其余项的误差率基本在3%以下;六阶简化模型的误差率最小,在0.005%以下,远小于规定的误差率阈值。由此说明简化频域Volterra级数的多点定位系统模型能够准确描述多点定位系统的输出特性。
2 基于核函数的S模式信号模型及误差分析
2.1 基于非线性系统核函数的S模式信号
非线性系统原理等效电路图如图3所示。为构建基于非线性系统核函数的S模式信号,设非线性系统输出特性为铁芯电感形式,可等效为图3所示的电路形式[7],其输入信号为图1(b)所示的S模式信号。
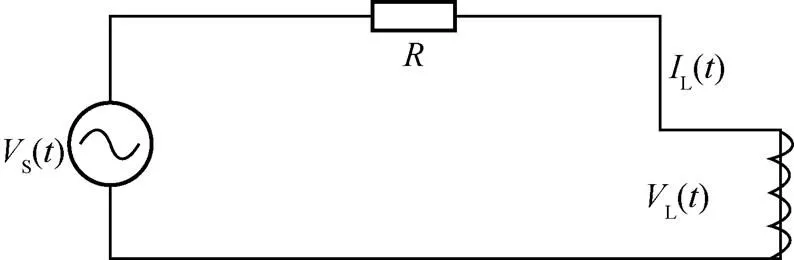
图3 非线性系统原理等效电路图
已知输入电压S()与输出电流L()之间满足[7]:

针对具有铁芯电感形式输出特性的非线性系统,输入1 090ES(1 090 extended squitter,1 090 MHz扩展电文)的S模式信号。S模式信号是周期性信号,每个周期中均包含8 μs前导脉冲和56/112 μs数据脉冲[16]。S模式信号中含有多次谐波,且基波项幅值大于谐波项幅值,所以可将S模式信号看作准正弦信号。铁芯电感形式输出特性的非线性系统要求输入信号大于0,故向S模式信号中加入直流项;考虑实际S模式信号一般是毫伏级别,故将铁芯电感形式非线性系统的输入信号单位换算为毫伏(mV)。综上,对S模式信号进行修改,修改后的S模式信号表示式为:
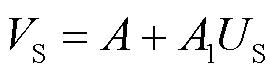
S表示含直流分量的S模式信号,表示直流项幅值,S表示幅值范围是−1~1 mV的S模式信号,1为系数。设=35 mV,1的范围是0.45~24.75 mV,取值间隔是0.45 mV。分析输入S模式信号时,一阶至十阶简化频域Volterra级数的非线性系统模型误差率,仍然需要输入55个幅值不同的S模式信号。由55个幅值不同的输入信号及对应的输出信号反推Volterra核函数,第七阶、第九阶和第十阶模型的第四至第六次谐波项对应的核函数值见表1。
为求解输入S模式信号时,简化频域Volterra级数的铁芯电感形式非线性系统模型误差率,设待验证信号是S1,计算式为:

一阶至十阶简化频域Volterra级数的铁芯电感形式非线性系统模型误差率的仿真结果如图4所示。
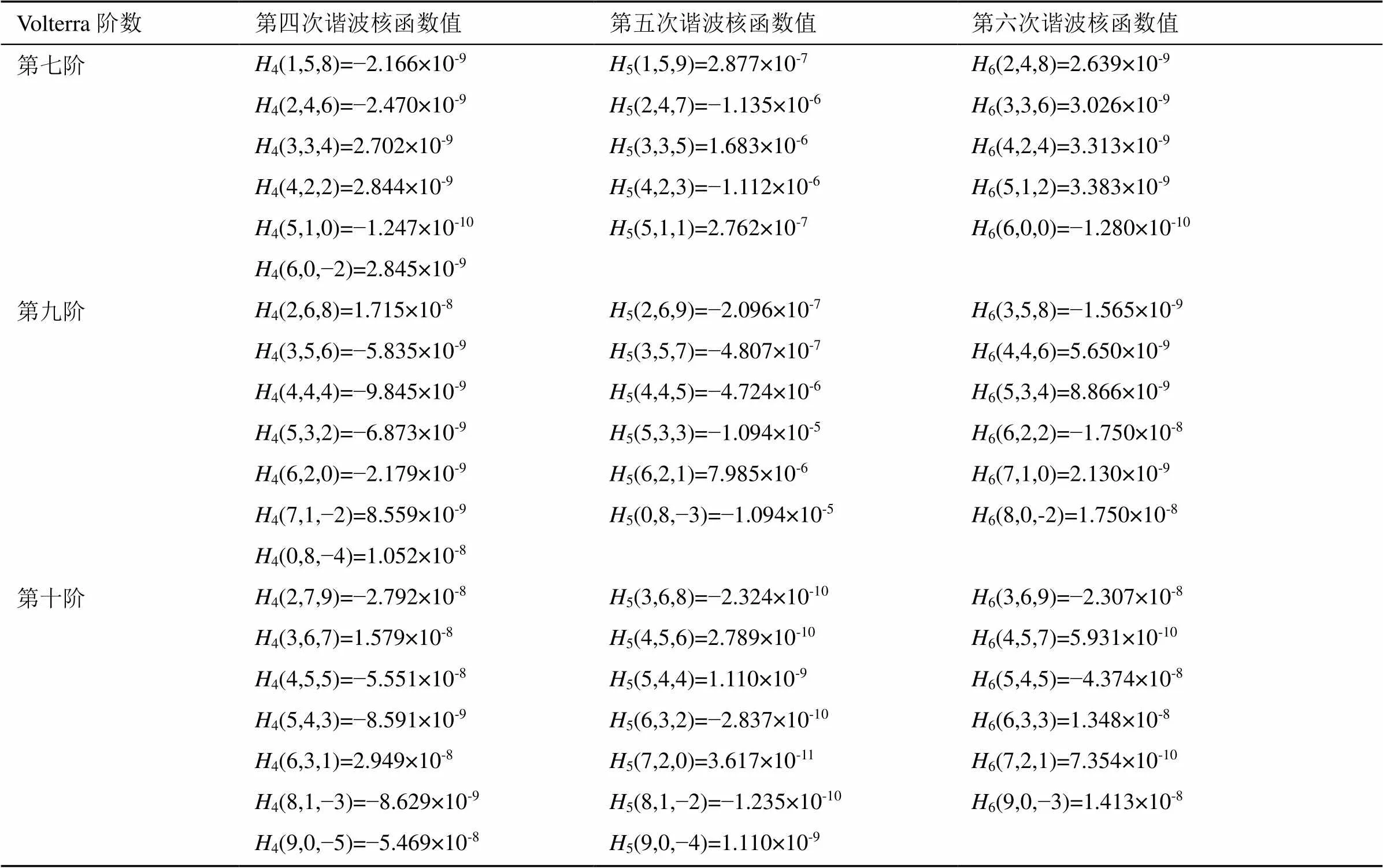
表1 第四次至六次谐波项对应的Volterra核函数值

图4 一阶至十阶简化频域Volterra级数的铁芯电感形式非线性系统模型误差率的仿真结果
由图4可知,当输入S模式信号时,一阶和二阶简化频域Volterra级数的铁芯电感形式非线性系统模型的误差率较大,三阶至十阶模型的误差率较小。但七阶、九阶和十阶简化模型的第五次谐波误差率明显高于其他次谐波,可以认定第五次谐波项误差率为异常值。由表1可得,第五次谐波项的核函数值与第四次、第六次谐波项的核函数值存在数量级的差距,进而造成第五次谐波项误差率远大于第四次、第六次谐波项误差率。直流项误差率最大约7.01%,而四阶简化模型的误差率最小,在0.25%以下。故四阶简化频域Volterra级数的非线性系统模型可以准确描述铁芯电感形式非线性系统的输出特性。
现对第五次谐波的核函数值进行修正。令表1中第七阶模型的第五次谐波核函数值缩小至1/100,第九阶模型的第五次谐波核函数值整体缩小至1/100,第十阶模型的第五次谐波核函数值整体扩大10倍。修正后的第五次谐波核函数值见表2。
对Volterra核函数值修正后,分析简化频域Volterra级数的铁芯电感形式非线性系统模型误差率。设待验证信号仍是S1,则一阶至十阶简化频域Volterra级数的铁芯电感形式非线性系统误差率的仿真结果如图5所示。

图5 一阶至十阶简化频域Volterra级数的铁芯电感形式非线性系统误差率的仿真结果

表2 修正后的第五次谐波核函数值
由图5可知,第七阶、第九阶、第十阶简化模型的第五次谐波误差率明显降低,此时高阶简化频域Volterra模型能够准确描述铁芯电感形式非线性系统的输出特性。
2.2 基于核函数S模式信号的MLAT接收系统误差分析
当输入信号是S模式信号时,通过求解非线性系统的核函数构建基于核函数的S模式信号,分析基于核函数S模式信号的MLAT接收系统模型误差率。设待验证信号为S2,计算式为:

基于核函数S模式信号的MLAT接收系统模型误差率仿真结果如图6所示。
由图6可知,基于核函数S模式信号的MLAT接收系统中,七阶至十阶模型的第五次谐波误差率不存在异常值;直流项的误差率最大约为105%,七阶至十阶模型的误差率均小于1.57%,远低于误差率阈值。故基于核函数S模式信号的MLAT接收系统可以准确描述MLAT接收系统的输出特性。
2.3 仿真结果分析
当输入基于核函数的S模式信号时,通过分析非线性系统模型误差率,可得以下结论。
●输入S模式信号时,简化频域Volterra级数的铁芯电感形式非线性系统模型误差率较小,但高阶模型中存在误差率异常值。通过对第五次谐波对应的核函数值修正,使其与第四次、第六次谐波对应的核函数值保持相同的数量级,能够降低第五次谐波项的误差率。
●通过Volterra核函数构建基于核函数的S模式信号。当输入基于核函数的S模式信号时,基于核函数S模式信号的MLAT接收系统可以准确描述MLAT接收系统的输出特性。
3 简化频域Volterra级数的S模式信号接收系统模型性能分析
3.1 简化频域Volterra级数的S模式信号接收系统误差分析
当输入基于核函数的S模式信号时,分别分析信噪比为20 dB、15 dB、10 dB时的简化频域Volterra级数的S模式信号接收系统模型误差率,设待验证信号仍是S2。
信噪比为20 dB、15 dB、10 dB时的一阶至十阶简化频域Volterra级数的S模式信号接收系统模型误差率仿真结果如图7所示。
图7(a)表示信噪比为20 dB时简化频域Volterra级数的S模式信号接收系统模型误差率。整体来看,七阶至十阶简化模型的误差率较大,在100%以上;一阶至六阶简化模型的误差率在100%以下;四阶简化模型的误差率最小,在15.7%以下,低于误差率阈值。说明输入基于核函数的S模式信号时,信噪比为20 dB的四阶简化频域Volterra级数的S模式信号接收系统模型可以准确描述MLAT接收系统的输出特性。

图7 一阶至十阶简化频域Volterra级数的S模式信号接收系统模型误差率仿真结果
图7(b)表示信噪比为15 dB时简化频域Volterra级数的S模式信号接收系统模型误差率。整体来看,六阶至十阶简化模型的误差率较大,在116.47%以上;一阶至五阶简化模型的误差率较小,在112.93%以下。二阶简化模型的误差率最小,在23.23%以下,低于误差率阈值。说明输入基于核函数的S模式信号时,信噪比为15 dB的二阶简化频域Volterra级数的S模式信号接收系统模型可以准确描述MLAT接收系统的输出特性。
图7(c)表示信噪比为10 dB时简化频域Volterra级数的S模式信号接收系统模型误差率。此时一阶至十阶简化模型的误差率均在94.6%以上,大于误差率阈值。说明输入基于核函数的S模式信号时,信噪比为10 dB的简化频域Volterra级数的S模式信号接收系统模型不能描述MLAT接收系统的输出特性。
随着简化频域Volterra级数的S模式信号接收系统模型信噪比减小,对应的模型误差率在增大,但误差分布状态相似,即低阶简化模型的误差率较小,高阶简化模型的误差率较大。信噪比为10 dB的简化频域Volterra级数的S模式信号接收系统模型误差率非常大,不能描述MLAT接收系统的输出特性。
分析信噪比为20 dB、15 dB、10 dB的二阶完整形式Volterra级数的S模式信号接收系统模型误差率,与简化频域Volterra级数的S模式信号接收系统模型误差率进行对比。不同信噪比、不同形式Volterra级数的S模式信号接收系统模型误差率对比如图8所示。
图8(a)、图8(b)、图8(c)分别表示信噪比为20 dB、15 dB及10 dB的二阶完整形式Volterra级数与简化频域Volterra级数的S模式信号接收系统模型误差率对比图。由图8可知,信噪比分别为20 dB和15 dB时,简化频域Volterra级数与完整形式Volterra级数的直流项与第五次谐波误差率相差较大,其余谐波的误差率相差较小;信噪比为10 dB时,简化频域Volterra级数与完整形式Volterra级数的第三次谐波与第五次谐波误差率相差较大,其余谐波的误差率相差较小。故比较信噪比分别为20 dB和15 dB时两种Volterra级数的直流项与第五次谐波误差率及信噪比为10 dB时两种Volterra级数的第三次谐波与第五次谐波误差率。以两种Volterra级数的误差率差值作为比较指标,差值大于0,说明简化频域Volterra级数的误差率更高;差值小于0,说明完整形式Volterra级数的误差率更高。不同信噪比的误差率差值见表3。
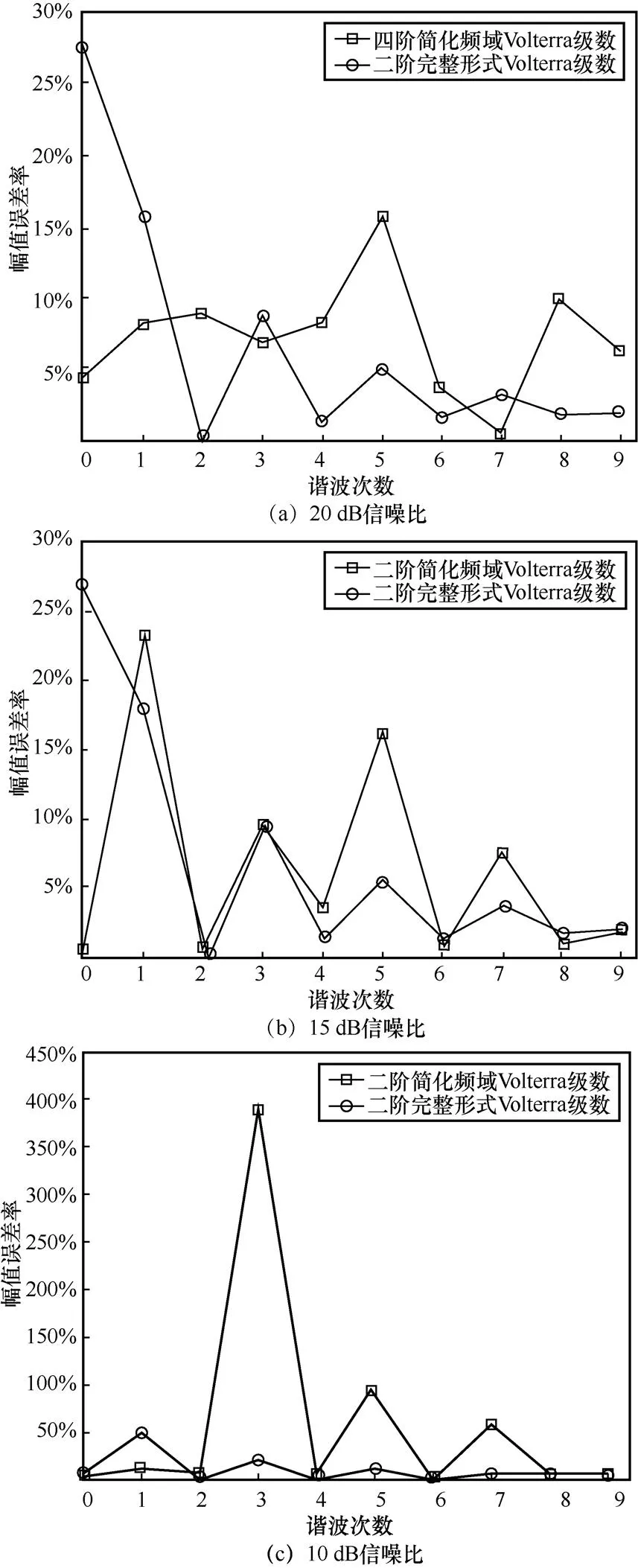
图8 不同信噪比、不同形式Volterra级数的S模式信号接收系统模型误差率对比

表3 不同信噪比的误差率差值
由表3可知,信噪比为20 dB时,两种Volterra级数的直流项误差率差值为−23.06%,第五次谐波误差率差值为10.56%。简化频域Volterra级数的第五次谐波误差率较高,但直流项误差率远低于完整形式Volterra级数。说明信噪比为20 dB时,四阶简化频域Volterra级数的S模式信号接收系统对MLAT接收系统输出特性的描述更准确。
信噪比为15 dB时,两种Volterra级数的直流项误差率差值为−26.56%,第五次谐波误差率差值为10.78%。简化频域Volterra级数的第五次谐波误差率较高,但直流项误差率远低于完整形式Volterra级数。说明信噪比为15 dB时,二阶简化频域Volterra级数的S模式信号接收系统对MLAT接收系统输出特性的描述更准确。
信噪比为10 dB时,两种Volterra级数的第三次谐波项误差率差值为370.24%,第五次谐波误差率差值为85.25%。简化频域Volterra级数的误差率明显高于完整形式Volterra级数的误差率。说明信噪比为10 dB时,二阶完整形式Volterra级数的S模式信号接收系统对MLAT接收系统输出特性的描述更准确。
以上说明,当信噪比大于15 dB时,简化频域Volterra级数的S模式信号接收系统对MLAT接收系统输出特性的描述准确度略优于完整形式Volterra级数的S模式信号接收系统;当信噪比为10 dB时,完整形式Volterra级数的S模式信号接收系统对MLAT接收系统输出特性的描述准确度略优于简化频域Volterra级数的S模式信号接收系统。说明完整形式Volterra级数的S模式信号接收系统对噪声的抗干扰能力更强。
3.2 实际S模式测试信号验证
使用MLAT系统中的实际S模式测试信号进行验证。对实际S模式测试信号进行归一化处理,一个周期的实测S模式信号如图9所示。

图9 一个周期的实测S模式信号
图9所示的信号的信噪比约为16.25 dB。当输入实际S模式测试信号时,一阶至十阶简化频域Volterra级数的S模式信号接收系统模型误差率仿真结果如图10所示。
由图10(a)可知,六阶至十阶简化频域Volterra级数模型的误差率最大,在55.7%以上;一阶至三阶简化模型的误差率较小,在44.9%以下,二阶简化模型的误差率最小在22%以下,低于误差率阈值。说明,当输入实际的S模式测试信号时,二阶简化频域Volterra级数的S模式信号接收系统模型可以准确描述实际的MLAT接收系统输出特性,且误差率低于规定的阈值。
图10(b)表示输入实际S模式测试信号时,二阶简化频域Volterra级数的S模式信号接收系统与二阶完整形式Volterra级数的S模式信号接收系统模型误差率对比图。由图10(b)可知,简化频域Volterra级数的第三次谐波误差率比完整形式Volterra级数低10.04%,直流项误差率低7.89%,第二次谐波误差率高8.17%,其余项的误差率相差较小。对比完整形式Volterra级数误差率,虽然简化频域Volterra级数的第二次谐波误差率较高,但直流项和第三次谐波的误差率较低。说明当输入实际S模式测试信号时,二阶简化频域Volterra级数的S模式信号接收系统模型对MLAT接收系统的输出特性描述更准确。
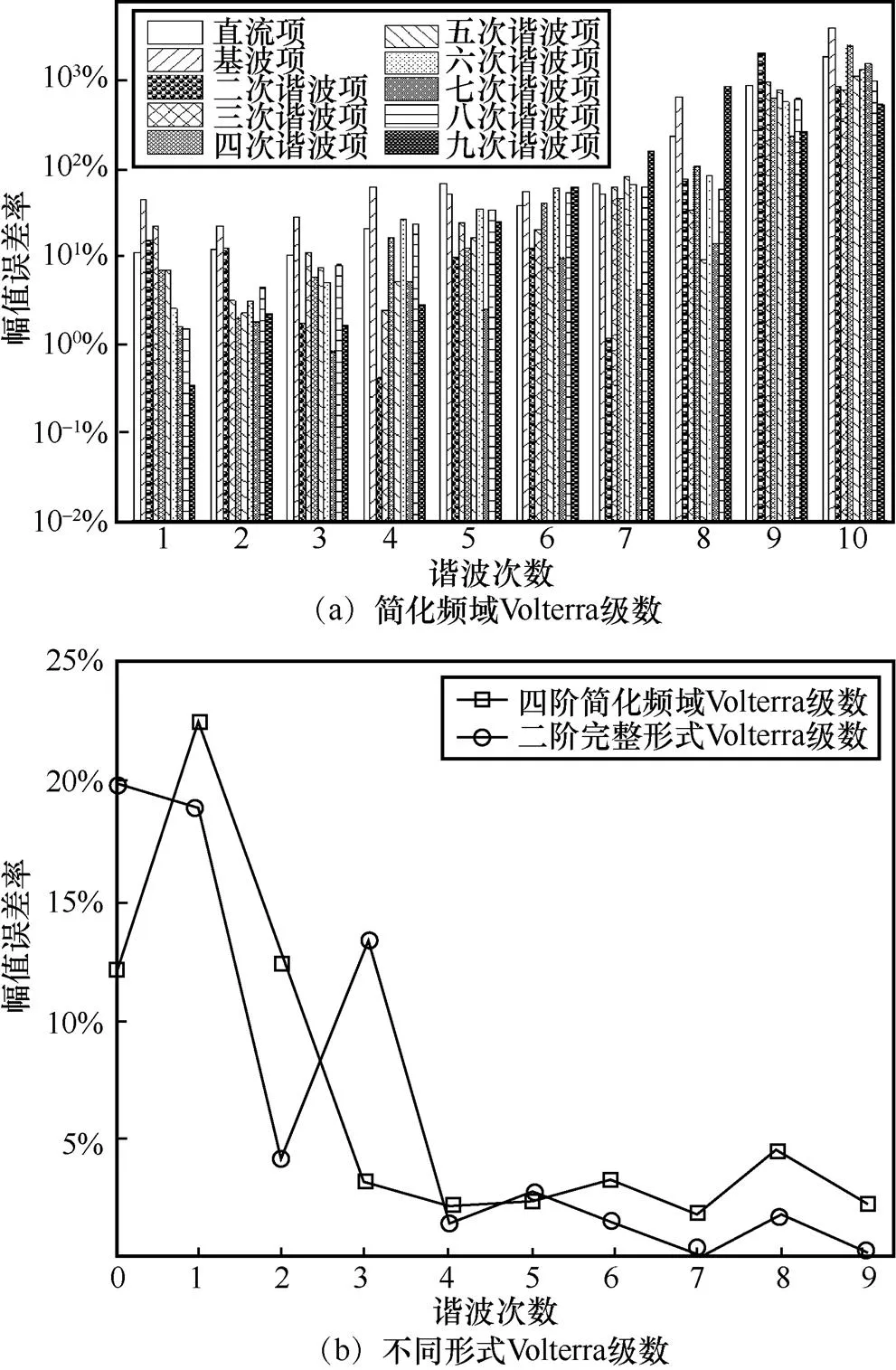
图10 一阶至十阶简化频域Volterra级数的S模式信号接收系统模型误差率仿真结果
4 结束语
研究基于简化频域Volterra级数的S模式信号多点定位系统特性,通过输入基于非线性系统核函数的S模式信号,分析简化频域Volterra级数的S模式信号接收系统模型误差率,结论如下。
●基于简化频域Volterra级数的接收机模型误差率在10.44%以下,小于误差率阈值。说明简化频域Volterra级数的多点定位系统模型可以准确描述多点定位系统模型的输出特性。
●当输入基于核函数的S模式信号时,简化频域Volterra级数的接收系统模型信噪比越小,误差率越大。当信噪比在15 dB以上时,该模型的误差率最小为23.23%,小于误差率阈值。说明当信噪比大于15 dB时,简化频域Volterra级数的S模式信号接收系统模型可以准确描述MLAT接收系统的输出特性。
●对简化频域Volterra级数的S模式信号接收系统模型进行实际测试。当输入信号是含有16.25 dB信噪比的实测S模式信号时,该模型的误差率最小在22%以下,小于误差率阈值。由此说明,基于简化频域Volterra级数的S模式信号接收系统模型可以准确描述实际的MLAT接收系统的输出特性。
[1] ANDREI A, VINCENZO R, VALERY V, et al. Trajectory phase-plane method - based analysis of stability and performance of a fuzzy logic controller for an anti-Lock braking system[C]//Proceedings of 2019 IEEE International Conference on Mechatronics (ICM), Piscataway: IEEE Press. 2019: 602-607.
[2] 何群, 邵丹丹, 王煜文, 等. 基于多特征卷积神经网路的运动想象脑电信号分析及意图识别[J]. 仪器仪表学报, 2020, 41(1): 138-146.
HE Q, SHAO D D, WANG Y W, et al. Analysis and intention recognition of motor imagery EEG signals based on multi-feature convolutional neural network[J]. Chinese Journal of Scientific Instrument, 2020, 41(1): 138-146.
[3] 陈森林, 高正红. 基于多小波展开的Volterra级数非线性系统建模方法[J]. 西北工业大学学报, 2017, 35(3): 428-434.
CHEN S L, GAO Z H. Nonlinear system modeling using multiwavelet expansion based volterra series[J]. Journal of Northwestern Polytechnical University, 2017, 35(3): 428-434.
[4] WEN W T, YE P, SONG J P, et al. A behavioral dynamic nonlinear model for time-interleaved ADC based on Volterra series[J]. IEEE Access, 2019(7): 41860-41873.
[5] 邱棚, 姚旭日, 李鸣谦, 等. Volterra级数模型的非线性压缩测量辨识算法[J].国防科技大学学报, 2020, 42(1): 125-132.
QIU P, YAO X R, LI M Q, et al. Nonlinear compressed measurement identification based on Volterra series[J]. Journal of National University of Defense Technology, 2020, 42(1): 125-132.
[6] AYDIN O. IMD analysis of the output section of an RF power amplifier using Volterra series[C]//Proceedings of the 2020 International Conference on Electrical, Communication, and Computer Engineering (ICECCE). Piscataway: IEEE Press, 2020: 1-5.
[7] FAIFER M, LAURANO C, OTTOBONI R, et al. Definition of simplified frequency-domain Volterra models with quasi-sinusoidalinput[J].IEEE Transactions on Circuits and Systems 2018, 65(5): 1652-1663.
[8] ALIZADAH M, AMIN S, RONNOW D. Measurement and analysis of frequency-domain Volterra kernels of nonlinear dynamic 3*3 MIMO systems[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66(7): 1893-1905.
[9] 武钰龙. 基于伏特拉级数的功放线性化技术研究[D]. 成都: 电子科技大学, 2020.
WU Y L. Research on linearization technology of power amplifier based on Volterra series[D]. Chengdu: University of Electronic Science and Technology of China, 2020.
[10] 李敏玥. 基于多项式的接收机非线性行为建模方法研究[D]. 西安: 西安电子科技大学, 2020.
LI M Y. Research on receiver nonlinear behavioral modeling method based on polynomial[D]. Xi'an: Xidian University, 2020.
[11] WARD E, MULGREW B. Baseband equivalent Volterra series for modelling cross-channel nonlinear distortion[C]//Proceedings of 2019 IEEE Radar Conference (RadarConf). Piscataway: IEEE Press, 2019: 1-4.
[12] 刘国华. 基于神经网络的接收机非线性行为建模[D]. 西安: 西安电子科技大学, 2021.
LIU G H. Nonlinear behavior modeling of receiver with neural network[D]. Xi'an: Xidian University, 2021.
[13] 李攀攀, 谢正霞, 乐光学, 等. 基于深度学习的无线通信接收方法研究进展与趋势[J]. 电信科学, 2022, 38(2): 1-17.
LI P P, XIE Z X, LE G X, et al. Research progress and trends of deep learning based wireless communication receiving method[J]. Telecommunications Science, 2022, 38(2): 1-17.
[14] 赵宏泽, 魏光辉, 杜雪, 等. 卫星导航接收机三阶互调阻塞效应分析[J]. 系统工程与电子技术, 2022, 44(4): 1336-1342.
ZHAO H Z, WEI G H, DU X, et al. Analysis of third-order intermediation blocking effect of satellite navigation receiver[J]. Journal of Systems Engineering and Electronics, 2022, 44(4): 1336-1342.
[15] FAIFER M, OTTOBONI R, PRIOLI M, et al. Simplified modeling and identification of nonlinear systems under quasi-sinusoidal conditions[J]. IEEE Transactions on Instrumentation and Measurement, 2016, 65(6): 1508-1515.
[16] 宫峰勋, 曹雅茹. S模式前导脉冲过零点提取与TOA时间戳精确度研究[J]. 南京航空航天大学学报, 2020, 52(5): 701-707.
GONG F X, CAO Y R. Zero-Crossing extraction of S-mode preamble plus and TOA timestamp accuracy[J]. Journal of Nanjing University of Aeronautics, 2020, 52(5): 701-707.
Characteristics of simplified frequency-domain Volterra series based S-mode receiver
GONG Fengxun, LI Jiankun
Civil Aviation University of China, Tianjin 300300, China
The nonlinear characteristics of multilateration(MLAT) system were analyzed by simplified frequency-domain Volterra series when the S-mode signal response pulse was input. Firstly, take the typical super heterodyne receiver system for example, the model based on simplified frequency-domain Volterra series and error rate model of MLAT system were explored and created. Secondly, the S-mode response pulse signal model based on kernel function was researched and established. Finally, the model error rate of S-mode signal receiver system based on simplified frequency-domain Volterra series was analyzed when the S-mode signal based on kernel function was input. The results show that the minimum error rate of the receiver system based on 15 dB SNR simplified frequency-domain Volterra series is less than 23.23% when the S-mode signal based on kernel function is input. When the actual S-mode test signal with 16.25 dB SNR is input, the minimum error rate of the model is less than 22%, which is less than the error rate threshold. It shows that the receiver system model based on simplified frequency-domain Volterra series can accurately describe the characteristics of S-mode signal receiver system, which provides the theoretical foundation for the identification of preamble arrival timestamp in MLAT system.
simplified frequency-domain Volterra series, S-mode signal, nonlinear system, kernel function
Key Research and Development Program of the Ministry of Science and Technology (No.2018YFC0809500)
TN851
A
10.11959/j.issn.1000−0801.2022153
2022−04−11;
2022−06−10
科技部重点研发计划项目(No. 2018YFC0809500)
宫峰勋(1965− ),男,中国民航大学教授、硕士生导师,主要研究方向为电磁辐射与电磁兼容、民航通信导航监视及多源数据融合等。

李建坤(1996− ),男,中国民航大学硕士生,主要研究方向为电磁辐射与电磁兼容。
