一种分析公路桩板式结构水平位移的简化方法

朱 俊

(1.安徽省交通规划设计研究总院股份有限公司，安徽 合肥 230088；2.公路交通节能环保技术交通运输行业研发中心，安徽 合肥 230088)

1 公路桩板式结构概述

安徽省首创的基于工业化建造的公路新型桩板式结构是在吸收既有桩板码头、铁路桩板路基的使用经验基础上，结合高速公路荷载特点进行创新，形成相关关键技术的新型桩板结构。

新型公路桩板式结构，是由工厂化生产的管桩、梁板组成的框架结构体系。预制板通过特有的连接装置支撑在管桩桩顶，桩间不填土，解决了征地困难、填土量大的问题，已成功应用于安徽省多条改扩建公路工程和新建公路工程[1]。

新型公路桩板式结构体系如图1所示。其为典型的框架结构体系，所有中墩均与梁板固结，联端设滑板支座。公路桩板式结构的设计难点在于联长的确定，需要准确分析各种荷载及作用引起的联端框架水平位移[2]，才能合理确定联长范围，确保结构安全与耐久。本文着重探讨了一种分析公路桩板式结构水平位移的简化方法。

图1 框架式公路桩板式结构体系

2 分析公路桩板结构水平位移的有限元法

2.1 精确有限元模型

采用Dr.Bridge有限元软件进行分析，按照实桥结构建立有限元二维分析模型。如图2所示的二维有限元分析模型以5跨为例，跨径6 m，柱高6 m，入土桩长10.5 m。

边界条件：

(1)联端采用活动铰支座。

(2)桩底固定。

(3)利用“m法”水平弹簧模拟地基土体对桩基的横向约束，其中填筑土，淤泥质粉质黏土的比例系数m值取4000 kN/m4，粉质黏土m值取7 000 kN/m4，碎石土m值取20 000 kN/m4，节点弹簧刚度K=b(桩计算宽度)×h(单元厚度)×m×y(单元深度)，详细模型如图2所示。

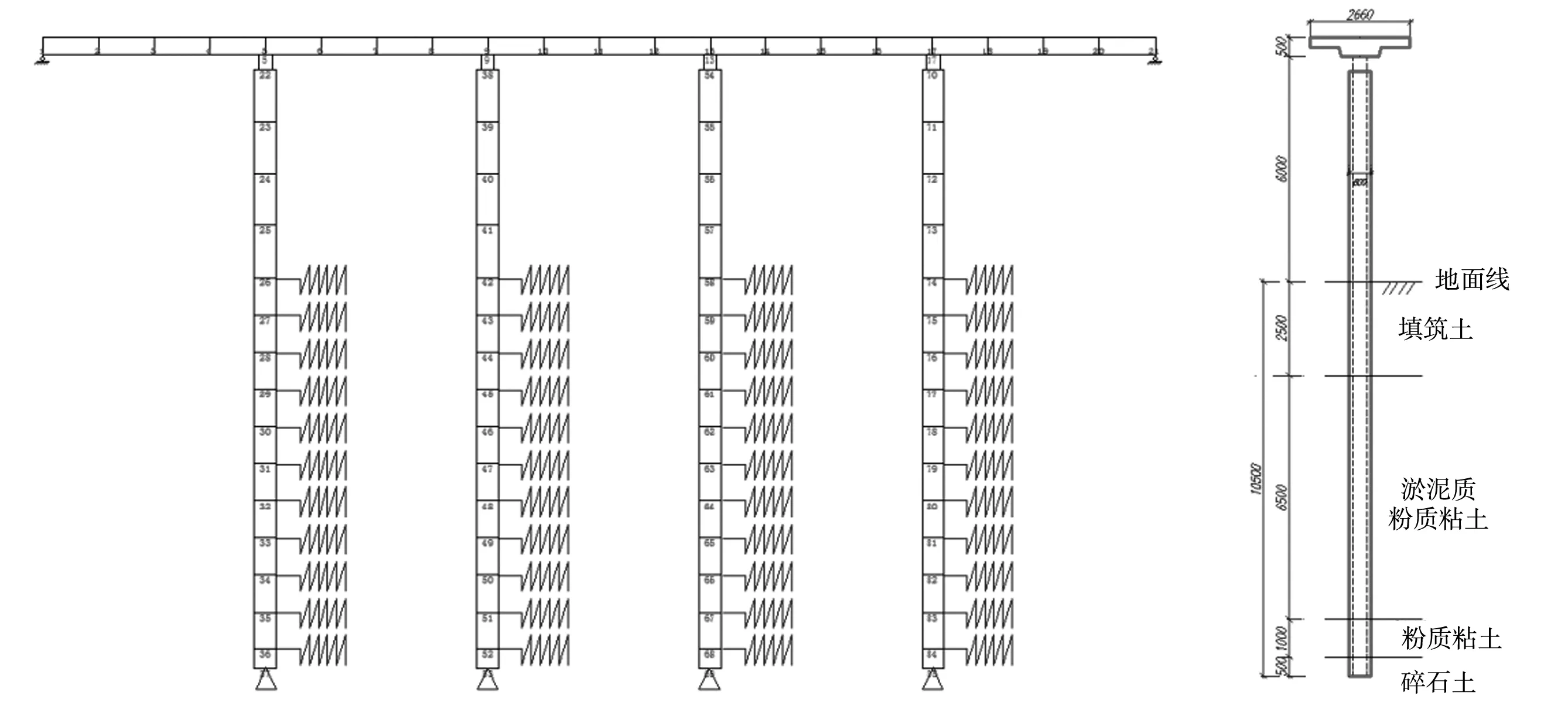
图2 二维精确有限元分析模型(以5跨为例)

2.2 简化有限元模型

以上精确有限元模型考虑了桩土相互作用，与结构实际几何模型一致，计算精度高，但土弹簧计算烦琐。当改变模型跨数时，建模周期长，效率低。为此，提出改良的换算桩长计算方法，对桩板结构计算模型进行简化。

依据“变形等效原理”将桩基简化为下端与地基固接的柱，以桩顶至第一个变形零点的距离作为等效柱长H，桩、柱的顶部变形值均为X0，因此可将桩和板一起等效为混凝土框架结构[3]。桩基水平变形曲线如图3所示。

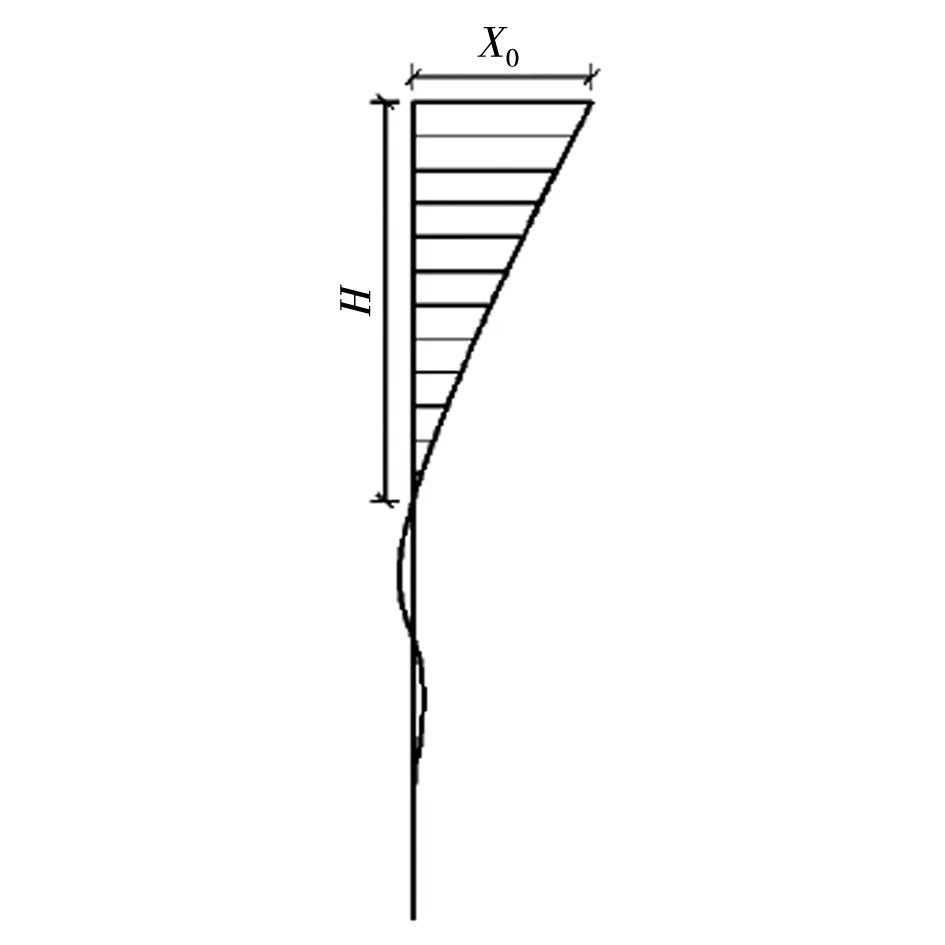
图3 桩基水平变形曲线

具体计算时，换算桩长可按实际桩土综合抗推刚度与换算桩抗推刚度相等的原则求得。在精确模型桩顶施加单位水平力1 kN，计算得到墩顶位移1.41 mm，按固端悬臂梁反算得到等效桩长(包括柱高)为9.5 m。简化后的二维有限元模型如图4所示。

图4 二维有限元简化分析模型(以5跨为例)

3 D值法——快速简便实用的理论计算方法

由以上二维有限元简化分析模型可以看出，其力学理论分析模型为平面框架，主要分析对象为平面框架在温度和制动力作用下的框架侧移，以下提出更为简便实用的一种框架侧移理论计算方法——“D值法”来替代有限元建模。当墩高、跨数等参数改变时，采用“D值法”分析框架侧移能大大减小有限元计算工作量，有效提升计算效率。

3.1 基本假定

(1)桥墩(管桩)视为下端固结，上端弹性固结的超静定梁。

(2)由温度、制动力等水平力所引起的墩顶位移先分别进行力学分析，然后进行内力叠加，不计这些力的相互作用影响。

(3)计算制动力时，各墩墩顶所受剪力按各墩等效抗侧移刚度D(墩顶产生单位水平位移的剪力)分配——简称“D值法”。

(4)计算温度变形时，桩墩对梁产生的弹性拉伸或压缩影响忽略不计，梁接近于自由变形。

基于基本假定的“D值法”简化计算模型如图5所示。

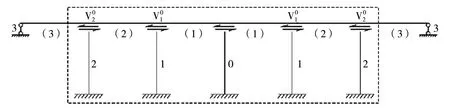
图5 “D值法”简化计算模型

3.2 计算步骤

3.2.1 等效抗侧移刚度D的计算

由结构力学经典位移法公式可知，两端固结的杆，当一端发生单位侧移时，引起的杆端剪力为12i/h2，i为线刚度，i=EI/h，则两端固结的杆抗侧移刚度D为：

理论简化计算模型中，桥墩(管桩)下端固结，上端为弹性固结(有转角)，非完全固结，故实际桥墩的等效抗侧移刚度D应进行修正[4]，修正公式为：

式中：αA是考虑了梁、柱刚度比值对侧移刚度影响的修正系数，具体推导见参考文献[5]；h为柱高。

3.2.2 制动力引起的墩顶位移计算

设桩板结构的总跨数为n，墩数则为(n-1)，根据假定c，则有：

式中：ViT为作用在第i墩墩顶的分配的制动力(剪力)；

T为全联承受的制动力；

Di为第i墩等效抗侧移刚度。

于是墩顶水平位移△iT为：

梁的联端的水平位移与边墩墩顶的水平位移相同。

3.2.3 梁的温度位移计算

只考虑年温差的作用，首先求出温度变化时梁的位移等于零时的位置。

根据假定c、d，导得该位移值为零的位置为：

式中：l为跨径，统一取6 m。

若全联墩高相同，则梁的位移零点位置在一联的正中。

如果用x0表示联端至位移零点的距离，x1表示1号墩(边墩)至位移零点的距离，xi表示i号墩至位移零点的距离，

则得联端由年温差引起的水平位移为：△0t=α×t×x0

由年温差引起的各墩墩顶水平位移为：△it=α×t×xi

式中：α为上部结构的线膨胀系数；

t为温度升降的度数，即当量温差。

4 数值计算与理论分析对比

将以上介绍的三种计算模型，即二维精确有限元分析模型、二维有限元简化分析模型、D值法理论解析模型，进行结果对比，分别建立了5×6 m(联长30 m)和10×6 m(联长60 m)两种联长状态下的三种计算模型，结果对比主要关注梁端水平位移、边柱顶水平位移、边柱顶剪力三个指标。具体结果见表1、表2：

表1 温差荷载作用[升(降)温25℃]下数值计算与理论分析结果对比

表2 制动力荷载作用下数值计算与理论分析结果对比

从对比结果可以看出，使用“D值法”理论解析模型可以得到足够精确的计算结果，其相对于有限元模型的误差均小于5%，完全可以代替有限元模型对桩板结构的水平位移进行分析。

5 结 语

温度与制动力是控制公路桩板式结构联长的重要因素。本文以联端位移、桩顶位移为定量控制指标，分析了温度与制动力对公路桩板式结构水平位移的影响，提出了一种分析公路桩板式结构水平位移的简化方法。分析时首先建立桩板结构的二维精确有限元分析模型，在精确模型基础上提出用“换算桩长法”对桩板结构计算模型进行简化，得到简化的二维有限元分析模型。最后，采用“D值法”对简化模型进行理论分析，得到位移计算的解析公式，其相对于有限元模型的误差均小于5%，完全可以代替有限元模型对桩板结构的水平位移进行分析，大大减轻了建模计算工作量。