基于可破碎颗粒的高填方碎石土地基强夯颗粒流数值分析

陈 南, 尚晓一, 吴 彪, 余 虔, 熊勇林

基于可破碎颗粒的高填方碎石土地基强夯颗粒流数值分析

陈 南1,2, 尚晓一3, 吴 彪4, 余 虔4, 熊勇林1,2*

（1.宁波大学 冲击与安全工程教育部重点实验室, 浙江 宁波 315211; 2.宁波大学土木与环境工程学院, 浙江 宁波 315211; 3.大连国际机场集团有限公司, 辽宁 大连 116033; 4.民航机场规划设计研究总院有限公司, 北京 100101）

依托某碎石土地基强夯工程, 通过PFC2D建立模拟碎石土地基在单点多次夯击作用下碎石颗粒破碎的过程. 结果表明: 相比于不考虑颗粒破碎, 考虑颗粒破碎情况下造成的强夯沉降更大, 模拟效果更好. 强夯过程中, 初始阶段主要是夯坑底部碎石颗粒发生破碎, 随着夯击次数增多, 颗粒破碎带逐渐向夯坑两侧发展, 破碎的碎石颗粒的广度和深度一定程度上与夯击能大小成正相关. 夯坑底部主要由破碎的块石颗粒与土颗粒嵌合形成壳状结构起到加固作用.

碎石土; 颗粒破碎; 离散元; 强夯

强夯工法在实践中已得到了广泛运用, 但其作用机理尚不清晰[1]. 目前对强夯的研究主要分为物理试验和数值模拟两种方向. 在物理试验方面, 许多学者针对不同的地质条件进行了现场试验, 得到了土体的动应力分布特征及其衰减规律[2-4]. 数值模拟主要分为有限元和离散元两种, 许多学者通过有限元软件模拟结合现场试验提出了不同条件下的有效加固深度经验公式[5-6], 但有限元模拟作为一种连续介质力学计算方法无法对土体中的孔隙率直接进行计算, 也无法考虑碎石土颗粒形状的影响. 颗粒流离散元能较好地模拟强夯过程中土体孔隙率的变化, 同时也可以根据现场的块石形状进行模拟, 能更好地反映实际碎石土地基强夯过程中土体的变化.

现有的离散元数值模拟强夯主要采用接触粘结模型和动力阻尼滞回模型[7-10], 将碎石视为不可破碎的刚体, 但实际工况中对于大夯击能强夯, 填埋的碎石常常容易出现颗粒破碎的现象[11], 从而使大颗粒碎石含量减少, 细粒增加, 改善级配, 提高承载能力. 目前考虑颗粒破碎的研究主要用于模拟室内试验方面[12-15], 对于强夯的研究目前还存在一定空白.

本文针对这一情况, 依托某碎石土地基强夯工程, 利用PFC2D离散元计算软件内置的平行粘结接触模型+线性接触模型模拟大颗粒碎石+土, 分别考虑了颗粒破碎和不破碎两种情况, 建立了能够模拟强夯过程的离散元数值模型, 从而研究6000和10000kJ两种能级强夯冲击下碎石颗粒破碎的发展趋势, 并对模拟结果进行了相应验证, 为今后研究碎石土地基强夯加固提供一种新的思路.

1 接触模型

(1)线性接触模型: 基于弹性理论建立的接触模型, 主要通过法向刚度和切向刚度来定义. (2)平行粘结接触模型: 在线性接触的基础上加入平行粘结接触, 颗粒之间可视为采用粘结键连接, 由粘结键负责传递力和力矩, 当其承受的力或力矩超过粘结力时, 粘结键发生断裂, 退化为线性接触. 接触模型如图1所示.

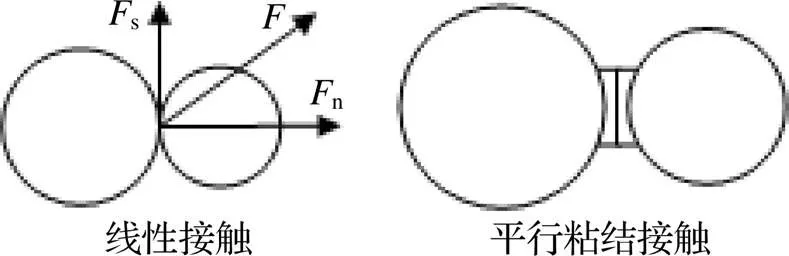
图1 接触模型

2 强夯模型

2.1 颗粒级配

PFC软件可较好地模拟材料的细观力学行为, 但使用离散元软件进行模型试验分析及工程分析时, 需要考虑计算精度与计算速率的平衡, 过大的颗粒尺寸跨度也容易导致计算时小颗粒悬浮使得计算不易收敛. 颗粒尺寸与模型尺度的相对大小以及颗粒粒径的最小值对颗粒数量影响最大.

图2为现场碎石土颗粒级配曲线, 直接使用初始建模级配建立的模型颗粒数量庞大, 计算效率过低, 故采用“等质量逐级替换最细颗粒”法[16]进行级配修正, 得到最终用于建模的颗粒粒组, 见表1.

图2 现场碎石土颗粒级配曲线

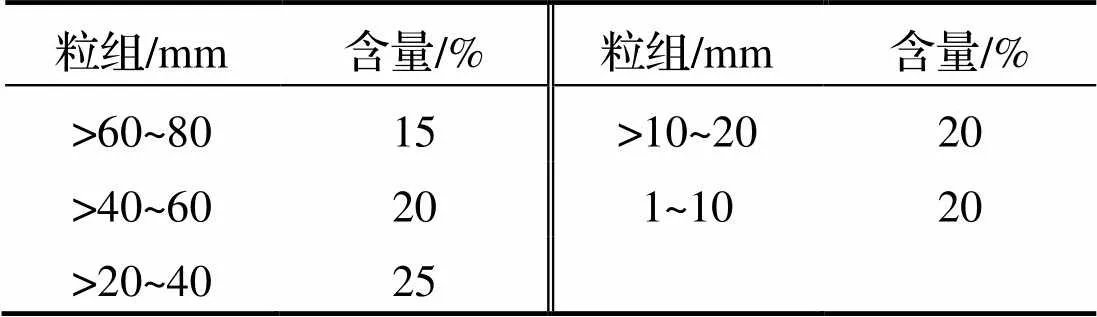
表1 模拟采用颗粒粒组

2.2 模型建立

在PFC2D程序中, 采用柔性簇(Cluster)模拟碎石, 圆盘颗粒(Ball)模拟土颗粒, 用Clump块组合5个Ball单元形成夯锤模型. 夯锤初始位置为地基模型上方0.5m处, 直径为2.5m, 初始速度为16 m·s-1, 根据工况的不同设置不同的夯锤密度. 考虑到实际工况中填土过程是分层进行的, 同时为了保证土体的均匀性, 共分5层从底部开始建模, 建立考虑颗粒破碎的Cluster+Ball地基模型. 同时建立不考虑颗粒破碎的纯Ball地基模型进行最终沉降对比, 其对应的模型颗粒总数为4614个.

综合考虑夯击能、夯锤直径以及颗粒尺寸对强夯的影响范围和数值计算效率的影响, 模型采用高25m、宽20m的墙体模拟数值模型的边界, 共52583个颗粒. 地基模型如图3所示, 其他细观计算参数见表2.

表2 颗粒流模型细观参数

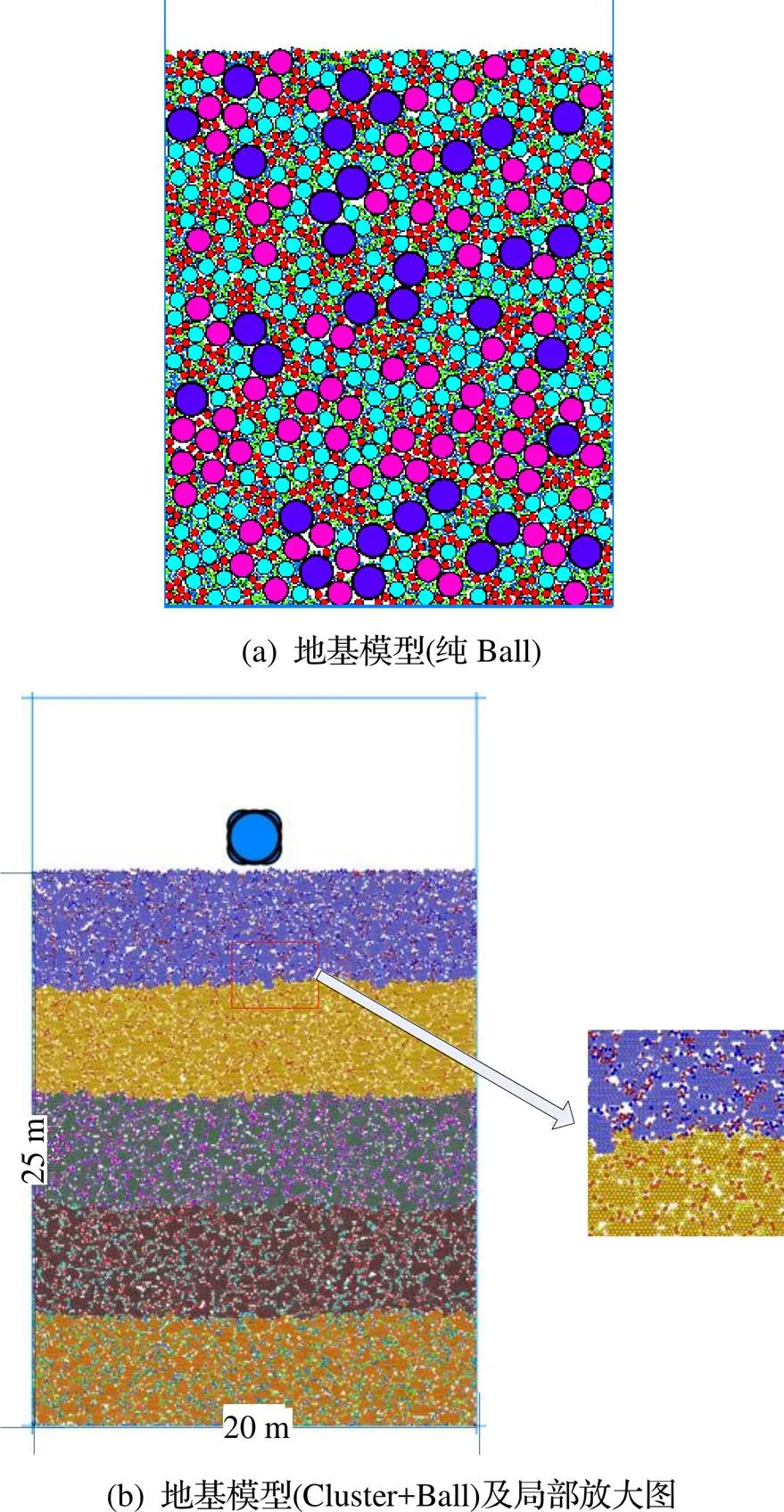
图3 数值模型

3 数值模拟及结果验证

3.1 计算流程

强夯计算可分为两个过程, 分别为成样和强夯, 具体步骤如下:

(1)根据预计的尺寸设置墙体作为计算模型的边界, 先根据级配由下至上分5层逐步成样建模;

(2)将刚性簇转换为柔性簇, 赋予表2中细观模型参数, 施加重力场, 以系统内不平衡力小于1.0×10-4N作为平衡指标, 平衡初始地应力, 直到系统达到平衡稳定状态;

(3)在模型中线上方设置夯锤, 在重力作用下自由落体, 为节省计算时间, 用低位赋予等效速度代替, 以夯锤速度小于0.01m·s-1, 保持夯沉量基本不变作为一次夯击试验的终止条件;

(4)在每次夯击完成后删去夯锤, 模型自平衡一定时间, 保证土体回弹时间;

(5)在土中每隔一定深度设立监测点, 监测土体位移时程;

(6)重复(3)、(4)过程, 进行多次夯击, 直到达到预计夯击次数或者其他设定条件.

3.2 强夯结果分析

为验证数值模型的可靠性, 将模型计算结果与现场监测结果进行对比. 现场共分为Ⅰ、Ⅱ两个试验区. Ⅰ区面积为60m×60m, 采用6000kJ夯击能进行试夯, Ⅱ区面积为120m×60m, 采用10000kJ夯击能进行试夯, 填料为附近爆破得到的开山石土. 现场采用履带式起重机进行夯锤吊装, Ⅰ区夯锤质量为47.94t, 对应夯锤落距为13.0m, Ⅱ区夯锤质量为61.98t, 对应夯锤落距为16.5m, 锤底直径均为2.5m. 模拟与现场试验结果对比如图4所示. 可以看到考虑碎石颗粒破碎情况的沉降相对于不破碎情况更接近现场试验结果, 6000和10000kJ对应的最终夯沉量为195.5和285.5cm. 与现场监测沉降量相比, 对应的最大夯沉量差值为15和26cm; 12次夯击累计沉降差值为2和26cm, 误差较小, 可认为本次模拟结果具有一定可信度.

由于该级配下对应的纯Ball模型的颗粒数较少, 仅为4614个, 计算效果上不如Cluster+Ball模型. Cluster+Ball模型颗粒数为52583个, 相当于纯Ball模型中的大粒径Ball单元转换成了Cluster柔性簇, 考虑到计算效率和级配对应性, 未对纯Ball模型颗粒数进行扩充. 图5为纯Ball模型夯击结束后的沉降结果.

图4 现场沉降结果与模拟结果对比

图5 纯Ball地基最终沉降

除地表夯坑沉降监测点外, 在模型的中线下方间隔一定深度分别布置6个监测点, 用来监测强夯过程土体的深层沉降, 监测结果如图6所示. 可以看到强夯主要的作用分为夯击沉降、土体回弹、土体平衡3个阶段, 两种工况的影响深度均主要在地下5m以内.

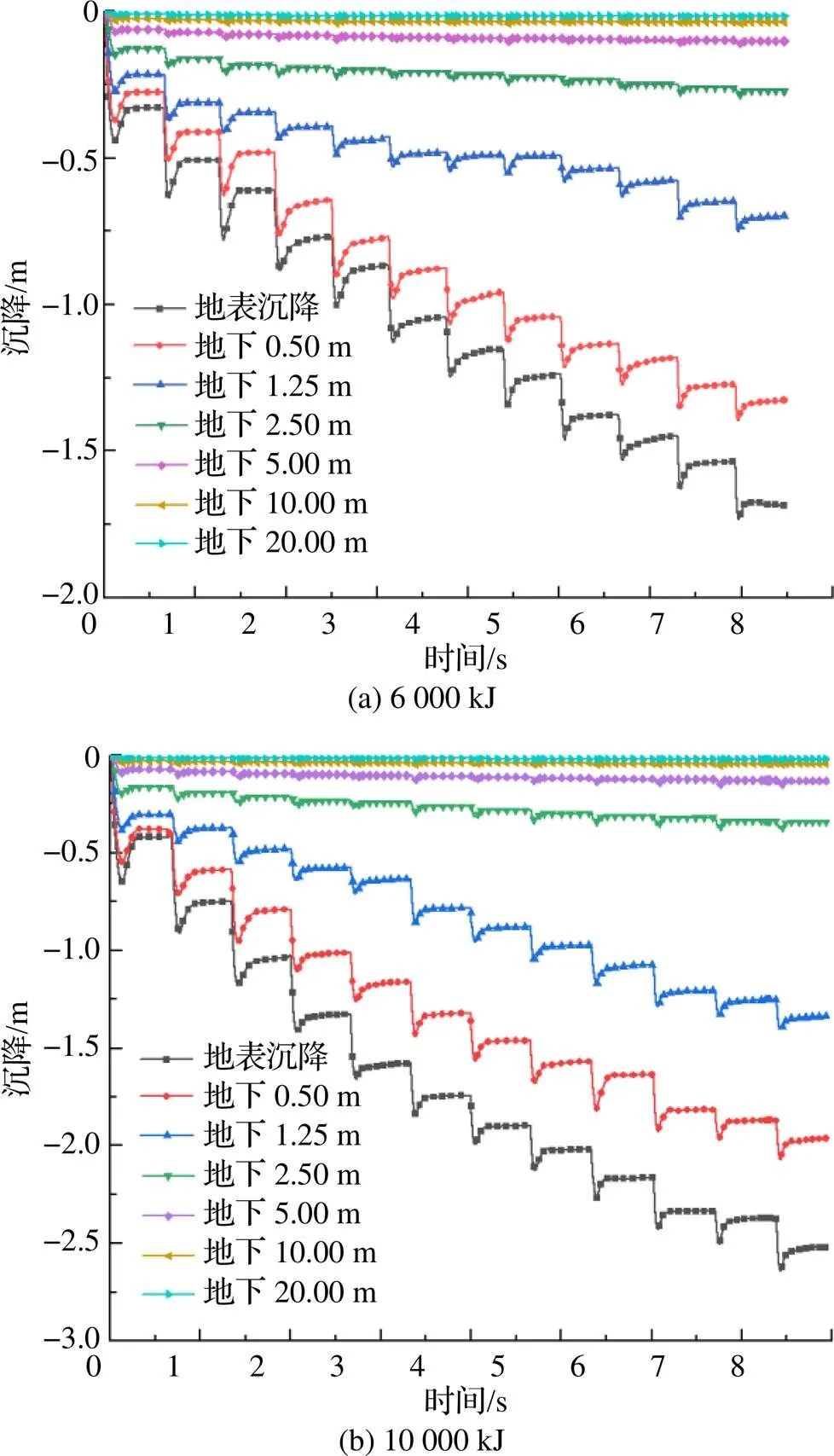
图6 各工况沉降曲线

夯击结束后模型的沉降云图如图7所示, 可以看到夯坑两端均出现了一定程度的隆起现象.

夯坑底面上部颗粒沉降较小是由于夯击过程中坑壁发生了一定程度的坍塌, 掉落到坑底的坑壁颗粒覆盖在了原有地表颗粒的上方, 并非初始阶段与夯锤接触的颗粒.

对比夯坑初始阶段与两种工况夯击结束的图像, 明显可以看到夯坑竖直方向的土体由于受到夯锤冲击作用, 颗粒之间孔隙变小, 破碎的碎石颗粒与土颗粒挤压形成壳状结构, 起到加固作用; 夯坑侧下方向表现为水平挤密作用, 同时发现夯坑坑壁出现一定程度的坍塌.

图7 夯击沉降云图

夯坑底部的碎石柔性簇受到冲击作用发生破碎, 由原来的簇状结构被压碎压平, 坑壁方向的柔性簇部分表现为从中间断裂的状态. 图8为两种工况强夯完成前后的颗粒状态图.

图8 夯击完成前后颗粒状态图

3.3 颗粒破碎分析

通过PFC2D内置的FISH语言对裂缝监测进行了二次开发, 以柔性簇内部粘结键破坏作为裂缝形成条件. 图9为夯击过程中产生的裂缝云图. 强夯造成的碎石破碎带初始主要分布在夯击坑下方, 随着夯击次数增多, 破碎带逐渐向夯坑两端发展. 由图可见, 强夯能级对颗粒破碎的影响主要表现在深度和广度上, 并在一定程度上呈正相关. 6000与10000kJ能级的第一击均造成碎石柔性簇破碎, 10000kJ能级造成的破碎明显更多, 强夯结束后10000kJ能级监测到的裂缝数几乎是6000kJ能级的两倍, 影响范围明显更广. 通过监测裂缝坐标数据, 10000kJ能级造成土中颗粒破碎的深度主要分布在夯坑底下2m左右, 6000kJ能级造成土中颗粒破碎的深度主要分布在夯坑底下1.5m左右.

图9 裂缝云图

模拟过程中发现两种工况的力链发展情况较为相似, 以10000kJ夯击能工况为例, 如图10所示, 初始状态即重力平衡状态下颗粒接触力链及大小分布较为均匀, 可以看到随着强夯次数增加, 土体中的力链逐渐向夯击坑中心集中, 呈放射状分布, 未破碎的碎石柔性簇相对土颗粒承担更多的轴向力, 同时力链逐渐向水平方向发展.

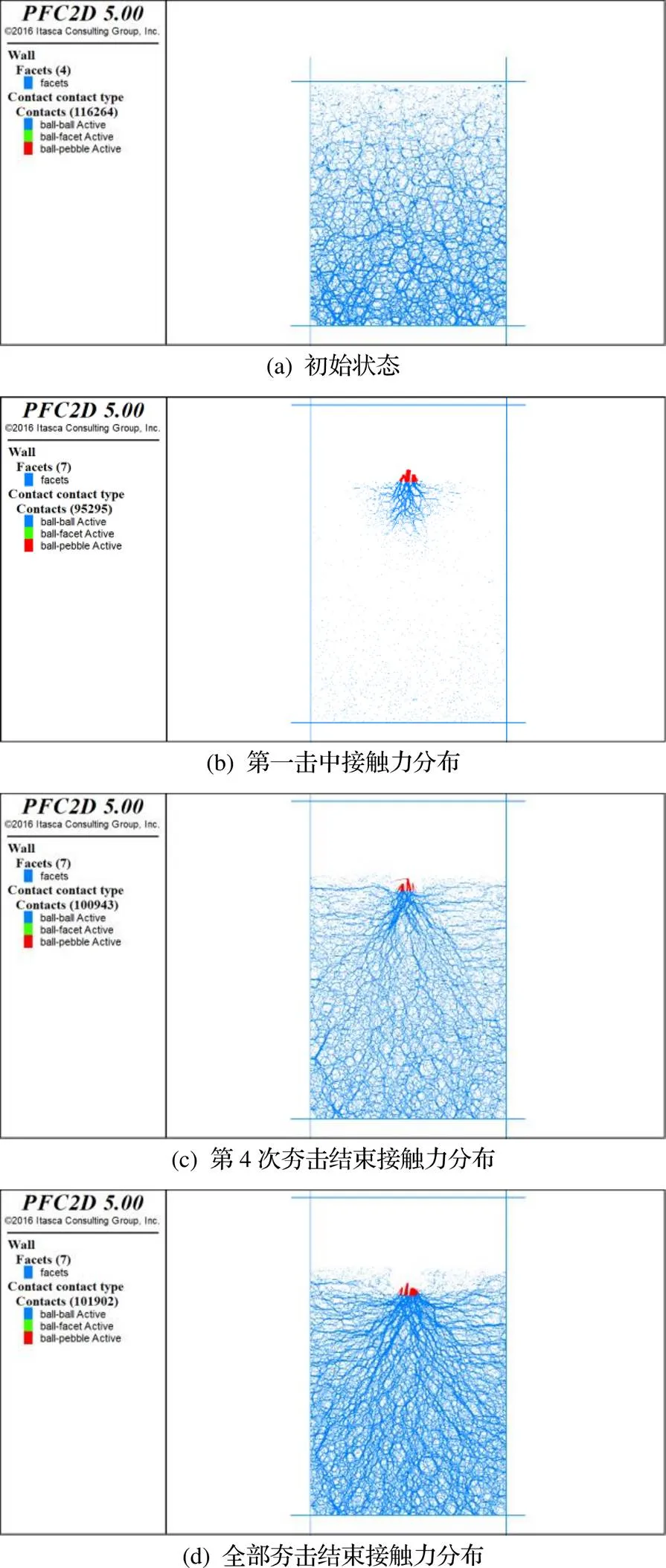
图10 10 000 kJ力链云图

4 结论

结合强夯现场试验, 利用PFC2D离散元软件建立了一个考虑碎石土地基强夯过程中颗粒破碎的数值模型, 探究碎石土地基强夯过程中碎石颗粒破碎的过程及发展趋势, 得到以下结论:

(1)相同参数下, 考虑碎石颗粒破碎比不考虑破碎造成的沉降更大, 相对更接近于实际沉降.

(2)碎石土地基强夯过程中, 夯坑底部主要由破碎的块石颗粒与土颗粒嵌合形成壳状结构起到加固作用, 夯坑侧方向土体表现为水平挤密.

(3)强夯过程中, 夯坑两端出现隆起现象, 同时随着强夯能级增大, 坑壁出现坍塌, 造成一定程度偏锤, 同时部分颗粒出现飞起现象.

(4)6000kJ对应的12次夯击最终沉降量为195.5cm, 与实际沉降误差为2cm, 约为1%, 10000kJ对应的12次夯击最终沉降量为285.5cm, 与实际沉降误差为26cm, 约为9%, 可认为本次模拟具有一定的可信度.

(5)强夯过程中, 初始阶段主要是夯坑底部碎石颗粒发生破碎, 随着夯击次数增多, 破碎带逐渐向夯坑两侧发展, 破碎的碎石颗粒的广度和深度一定程度上与夯击能大小成正相关.

[1] 周梦佳, 宋二祥. 高填方地基强夯处理的颗粒流模拟及其横观各向同性性质[J]. 清华大学学报(自然科学版), 2016, 56(12):1312-1319.

[2] 年廷凯, 李鸿江, 杨庆, 等. 不同土质条件下高能级强夯加固效果测试与对比分析[J]. 岩土工程学报, 2009, 31(1):139-144.

[3] 宋修广, 周志东, 杨阳, 等. 强夯法加固无黏性土路基的现场试验与数值分析[J]. 公路交通科技, 2014, 31(3): 1-6; 37.

[4] 胡长明, 梅源, 王雪艳. 离石地区湿陷性黄土地基强夯参数的试验研究[J]. 岩土力学, 2012, 33(10):2903- 2909.

[5] 高政国, 杜雨龙, 黄晓波, 等. 碎石填筑场地强夯加固机制及施工工艺[J]. 岩石力学与工程学报, 2013, 32(2): 377-384.

[6] 赵家琛, 吕江, 赵晖, 等. 高能级强夯处理抛填路基的有效加固深度[J]. 土木与环境工程学报(中英文), 2021, 43(5):27-33.

[7] 马宗源, 徐清清, 党发宁. 碎石土地基动力夯实的颗粒流离散元数值分析[J]. 工程力学, 2013, 30(S1):184- 190.

[8] 贾敏才, 王磊, 周健. 干砂强夯动力特性的细观颗粒流分析[J]. 岩土力学, 2009, 30(4):871-878.

[9] 贾敏才, 吴邵海, 叶建忠. 基于三维离散元法的强夯动力响应研究[J]. 湖南大学学报(自然科学版), 2015, 42(3):70-76.

[10] 李希, 张勋, 马新岩, 等. 土石混合填料强夯过程三维离散元模拟[J]. 北京交通大学学报, 2020, 44(3):88-92; 108.

[11] 张清峰, 王东权, 王伟. 强夯加固煤矸石地基破碎密实机理探讨[J]. 建筑科学, 2010, 26(7):13-16; 79.

[12] 刘新荣, 涂义亮, 王鹏, 等. 基于大型直剪试验的土石混合体颗粒破碎特征研究[J]. 岩土工程学报, 2017, 39(8):1425-1434.

[13] 张文力. 循环载荷作用下碎石集料的力学特性及宏细观破裂机理研究[D]. 徐州: 中国矿业大学, 2019.

[14] 付乐. 工程碎石土基本力学特性与强夯加固机理研究[D]. 北京: 北京科技大学, 2016.

[15] 雪青华. 土石混合体直剪特性及颗粒破碎特征研究[D]. 徐州: 中国矿业大学, 2020.

[16] 曹智. 砂泥岩及其颗粒料力学特性PFC模拟方法研究[D]. 重庆: 重庆交通大学, 2016.

Numerical analysis of dynamic compaction particle flow of high fill gravel foundation based on broken particles

CHEN Nan1,2, SHANG Xiaoyi3, WU Biao4, YU Qian4, XIONG Yonglin1,2*

( 1.Key Laboratory of Impact and Safety Engineering of Ministry of Education, Ningbo University, Ningbo 315211, China; 2.School of Civil and Environmental Engineering, Ningbo University, Ningbo 315211, China; 3.Dalian International Airport Group Co., Ltd., Dalian 116033, China; 4.China Airport Planning & Design Institute Co., Ltd., Beijing 100101, China )

Based on a dynamic compaction project of gravel soil foundation, the crushing process of gravel particles under single point and multiple tamping is simulated by PFC2D. The results show that the dynamic compaction settlement caused by considering particle breakage is larger than that without considering particle breakage, and the simulation effect is better. In the dynamic compaction process, the initial broken gravel particles are mainly concentrated at the bottom of the tamping pit. With the increase of tamping times, the particle crushing zone gradually develops to both sides of the tamping pit. The breadth and depth of broken gravel particles are positively correlated with the tamping energy to some extent. The bottom of the rammed pit is mainly composed of broken stone particles and soil particles to form a shell structure to reinforce.

gravel soil; particle breakage; discrete element; dynamic compaction

2022−02−24.

宁波大学学报（理工版）网址: http://journallg.nbu.edu.cn/

宁波大学冲击与安全工程教育部重点实验室开放基金（CJ-20180110）.

陈南（1996－）, 男, 浙江温州人, 在读硕士研究生, 主要研究方向: 岩土数值计算. E-mail: 371257313@qq.com

通信作者:熊勇林（1989－）, 男, 江西南昌人, 副教授, 主要研究方向: 土力学. E-mail: xiongyonglin@nbu.edu.cn

TU411.5

A

1001-5132（2022）04-0058-07

（责任编辑 韩 超）