基于数字高程模型的雷达探测威力计算方法
2022-07-07费晓超
费晓超
(南京国睿防务系统有限公司 江苏省南京市 210012)
1 引言
现代战争中,为了提高战机的生存能力和突防成功概率,面对敌方的探测雷达进行低空或超低空突防时,需要以最小的被探测风险通过雷达的威胁空间。探测雷达由于地形遮蔽、地球曲率以及地面杂波干扰等因素的影响会产生探测肓区,在进行突防航迹规划过程中要充分考虑敌方雷达探测威力,并尽可能利用地形遮蔽盲区来避开敌方探测[1]。实际探测威力的计算比较复杂,其中地形因素对雷达探测效果的影响较大,是雷达部署及突防作战必须考虑的因素。因此,快速获得基于地形遮蔽的雷达探测威力对突防飞机显得尤为重要。关于雷达探测盲区的方法[2-6]主要是建立一个以雷达为中心构简化地形模型或极坐标辅助模型,然后比较各方位线上的雷达探测高度和地点高度,从而得到雷达地形遮蔽盲区。这类方法基本可以判断出雷达地形遮蔽,但是对于复杂地形建模不够准确,模型数据与实测地形数据并不完全符合,难以说明雷达的实际探测性能。本文基于高精度的数字高程模型(Digital Elevation Model, DEM)数据,首先将包含经纬高信息的DEM数据从空间直角坐标系转换到雷达极坐标下,然后将雷达探测范围在方位和距离上网格化,依次计算各方位网格上指定目标高度的雷达探测威力,最后形成全方位的雷达探测威力,还可以进行多高度层的雷达探测威力计算。本文方法可以真实反应雷达的实际探测性能,为突防任务的航迹规划与威胁评估提供关键依据。
2 雷达探测威力影响分析
突防飞机通常采用超低空方式,利用敌方地面雷达盲区达到隐身目的。雷达探测盲区主要由地球曲率、地形遮蔽和地杂波干扰等因素产生,这些因素最终影响雷达的探测威力。
2.1 地球曲率
雷达工作时电磁波在空间中以直线传播,然而实际的地球表面是一个曲面而非平面,地球曲率对于雷达波束的指向和覆盖有着不可忽略的影响。如图1所示,假设雷达天线架设高度为HR,目标飞机高度为HT,Rd为考虑大气折射后的等效地球半径。若该目标位置与雷达位置连线刚好处与地表面相切,则图中的阴影区域即为地球曲率引起的雷达探测盲 区,该区域内的目标无法被雷达探测到,此时雷达位置与切点的直线距离即为雷达视线距离RS。
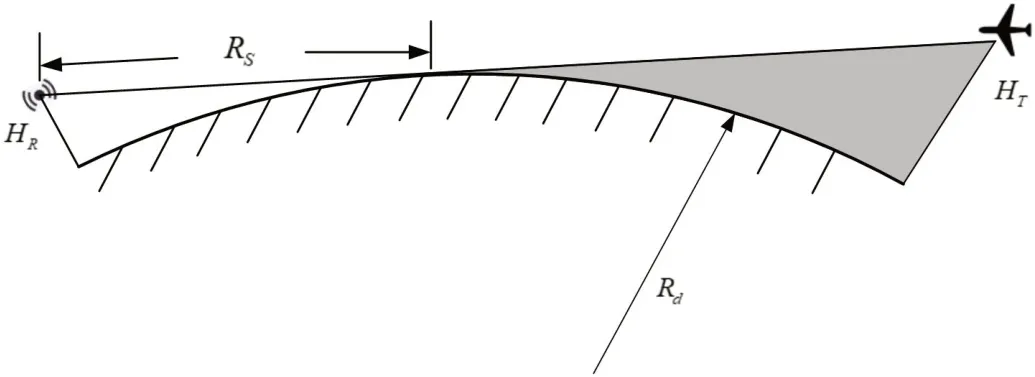
图1:地球曲率引起的探测盲区
雷达视线距离由天线高度HR和目标高度HT决定,可表示为[7]:

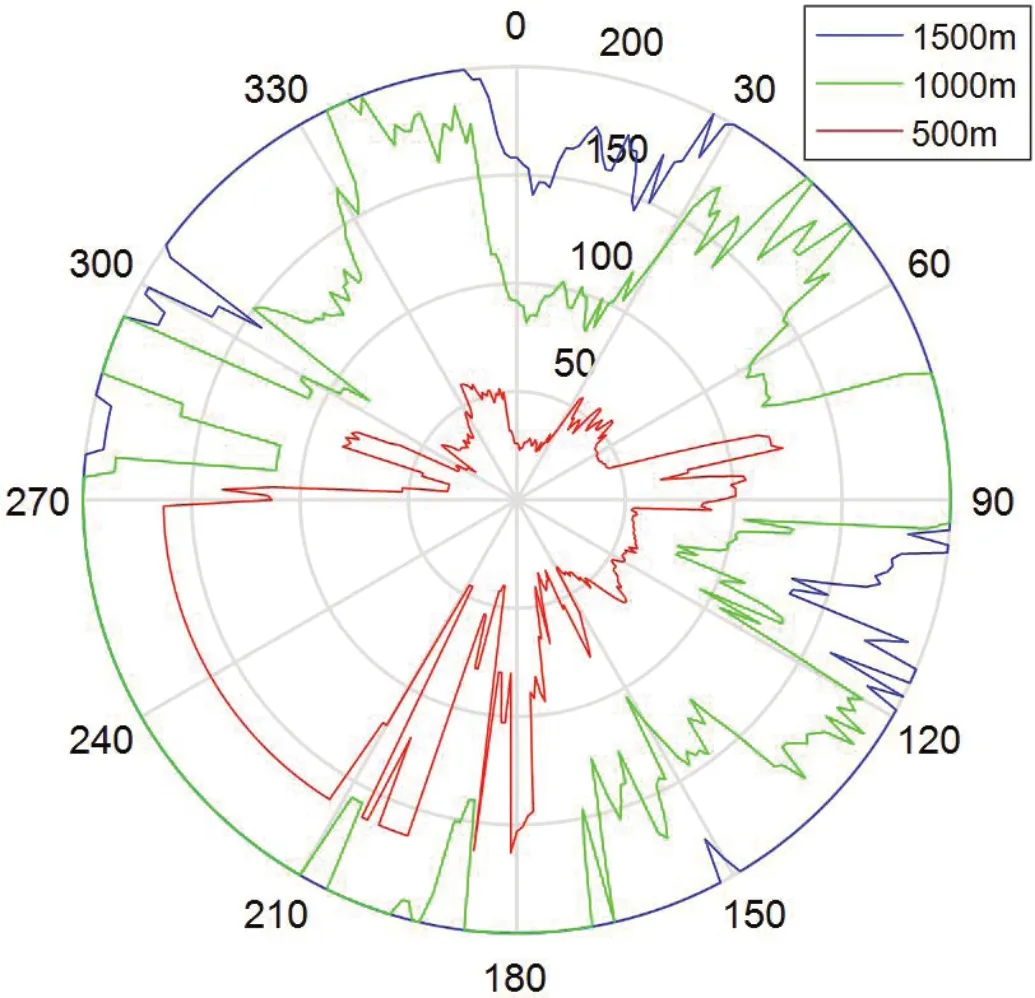
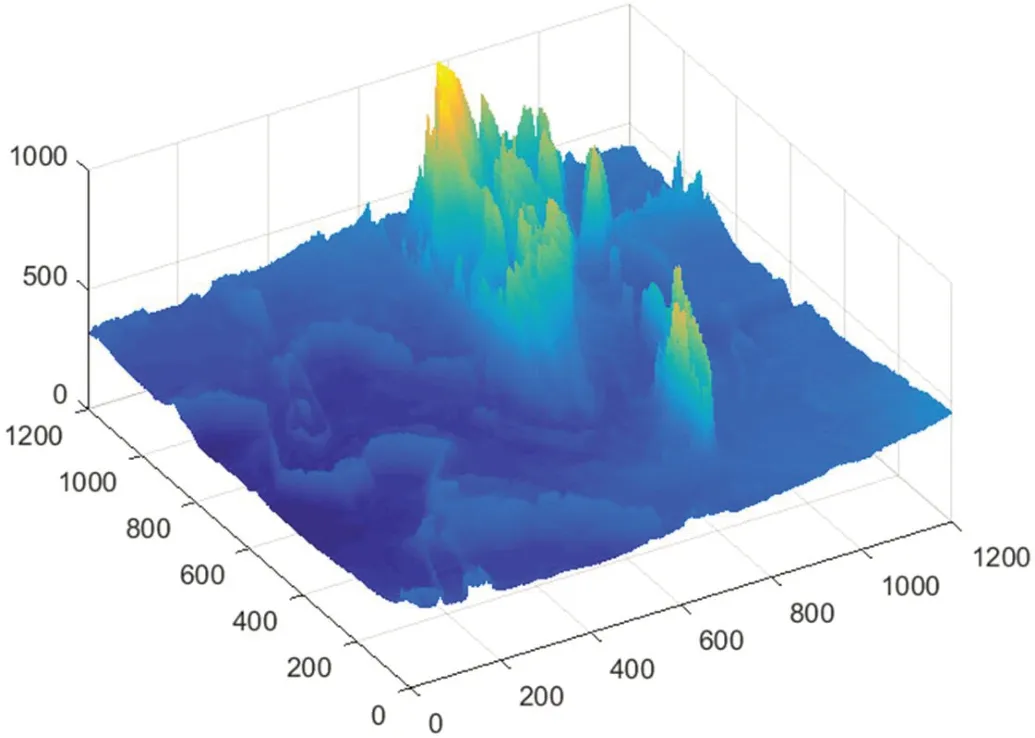
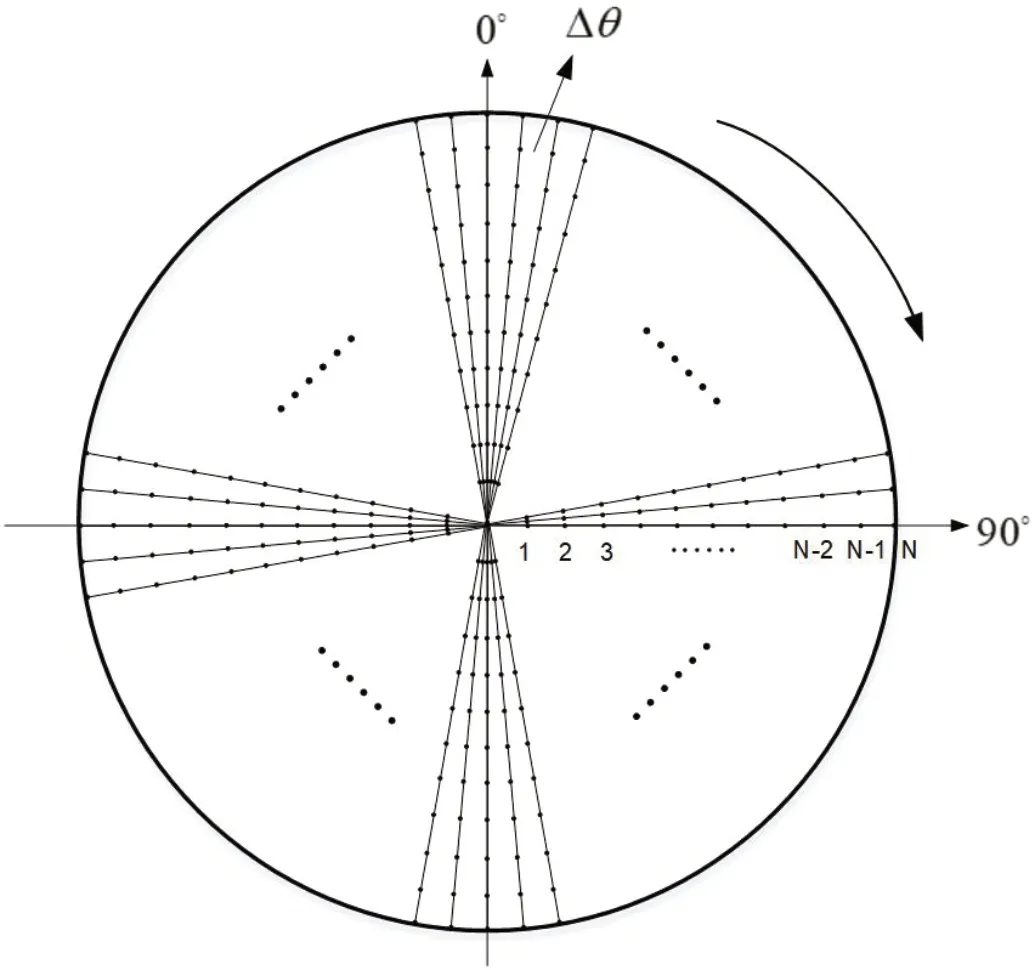
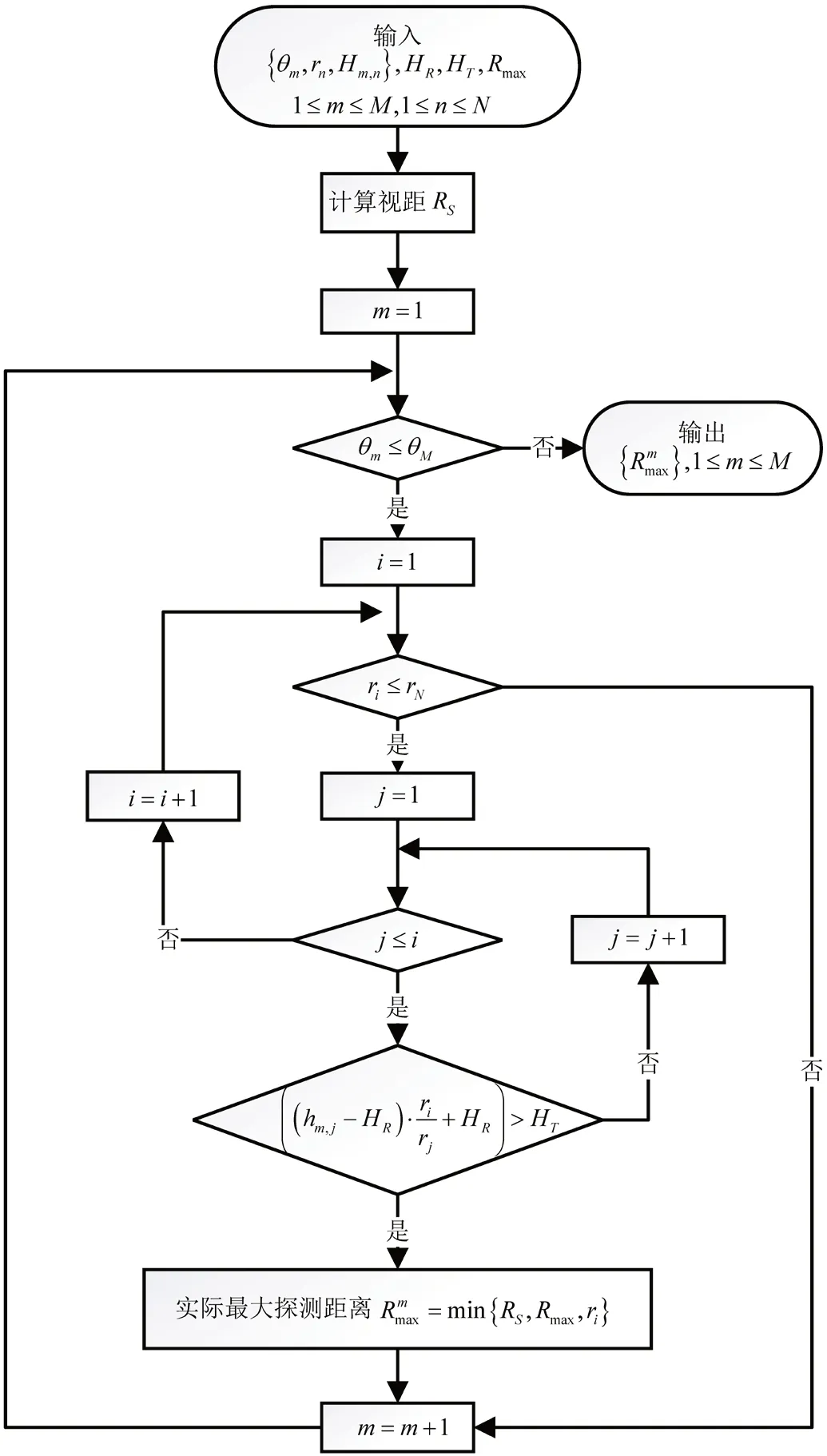
已知雷达的最大作用距离为Rmax的情况下,如果Rmax>RS,说明地球曲率限制了雷达的最大探测距离;反之,如果Rmax 雷达电磁波在空间传播过程中被起伏的地形表面和地面障碍物遮挡,形成地面雷达在有效作用距离内不能到达的空间,即雷达地形遮蔽盲区(如图2所示),从而导致雷达无法发现突防至其探测范围内的飞机。在山区或地表起伏不定的环境下,不可避免地存在雷达地形遮蔽盲区,无人机任务规划系统可以利用这种有利条件规划突防航线。雷达地形遮蔽盲区与雷达天线位置和雷达探测范围内的地形起伏情况有关。 图2:雷达地形遮蔽盲区 突防飞机在复杂地形上空作超低空飞行时,由于地表面起伏很大,雷达回收的地杂波功率很强,雷达波作用在飞机的反射信号被地杂波掩盖,形成了地杂波盲区。地杂波盲区是由飞机在雷达作用范围内具有50%被发现概率的空间点构成,具体计算过程见文献[8-9]。地杂波盲区与地面粗糙度、雷达波波段、飞机的雷达反射面积(Radar Cross Section, RCS)和飞机飞行高度有关。 与地杂波相比,决定雷达地形遮蔽盲区的因素具有数量少、容易确定和容易精确描述等特征,而与地面雷达的灵敏度、分辨率、雷达波长、波束形状、大气湿度以及地面的粗糙程度无关,具有全隐身性能好、隐身状况稳定、容易计算和精确判断等优点。在雷达天线位置固定时,地形遮蔽盲区的状态不随时间变化。因此,突防飞机应尽量利用雷达地形遮蔽盲区来进行全隐身突防飞行,本文方法只考虑在地球曲率和地形遮蔽影响下的雷达探测威力。 DEM是对地球表面地貌的一种离散的数学描述,它是表示区域D上的三维向量有限序列{Vi=(xi,yi,zi),i=1,2,3,…, n},其中,平面坐标zi是(xi,yi)对应的高程[10]。当该序列中各向量的平面点位坐标是规则格网排列时,则其平面坐标可省略,此时,DEM就简化为一维向量序列{zi,i=1,2,3,…,n}。 本文采用的高精度DEM数据由若干个数据块组成,每个数据块大小为经纬度1°×1°,在经度和纬度方向分别细化为1200份,即分辨率为 。1°×1°的数据块划分为1201×1201个点,每个点代表一组经度、纬度、高度数据如图3所示。 图3:高程数据块三维图(1°×1°) 根据雷达所在经纬度,找到该点所在数据块。定位雷达坐标所在DEM数据块后,根据雷达的最大作用距离Rmax,以该数据块为中心,读取经纬度±δ的地图数据拼成一个大数据块,记作保证覆盖360°雷达作用范围。 基于常用的雷达操作界面,雷达极坐标以雷达所在位置为圆心,正北方向为方位0°,方位按顺时针方向增加,雷达最大作用距离为Rmax。把雷达极坐标覆盖范围网格化,方位上间距Δθ,共分成M=360°/Δθ份,每个方位在距离上间距Δr,共分成N=Rmax/Δr份。因此,雷达最大探测距离覆盖范围下共被划分成M×N个点,如图4所示。 图4:雷达极坐标网格划分示意图 由于原始的DEM数据是在空间直角坐标系下的,为了计算过程的便捷性和准确性,需要把DEM数据转换成雷达极坐标系下的数据。在知道空间直角坐标系下经度、纬度、高度数据的情况下,极坐标下点的高度Hm,n需要通过坐标转换找到在空间直角坐标下对应的经纬度。假设某点在雷达极坐标下方位、距离、俯仰为雷达所在的点经度、纬度、高度为则转换过程可以通过以下步骤得到: 本文通过平面的极坐标点计算其经纬度,并根据经纬度查找对应的高度,因此令俯仰角φ=0。经过以上步骤,计算得到极坐标下该点的经纬度(α,β),找到该经纬度的在数据块中对应的高度。由此可以得到一组雷达极坐标下的地形高程数据M为方位扇区数,N为距离点数。 若存在j满足式(5)条件,则表示雷达在高度HT下受地形遮蔽影响的最大探测距离为ri。此时,该方位扇区最大探测距离为ri,综合考虑视距和最大作用距离,则方位扇区m实际雷达最大探测距离为 由此方位扇区计算结束,进入下一个扇区,M个方位扇区依次按上述方法计算,最终可以得到一组高度下全方位的雷达最大探测威力数据 。本文方法计算流程如图6所示。 图5:雷达遮蔽盲区判断计算示意图 图6:本文方法计算流程图 为了验证本文算法的可行性,本节将通过仿真实验对计算结果进行验证。本文使用C++实现了整个计算过程,最后通过MATLAB图形展示雷达探测威力。设置雷达站位置为东经3.114713°,北纬26.907825°,雷达天线高度为300m,最大作用距离为200km,以雷达站址为中心,其覆盖范围内的地形DEM数据三维图如图7所示。计算过程中设置方位间距Δθ=1°,距离间距Δr=200m,分别计算500m、1000m、1500m三个高度层下雷达探测威力,结果如图8所示。 图7:雷达作用距离内的极坐标DEM三维图 图8:不同高度层下雷达探测距离 对比不同高度遮蔽盲区及对照三维模型可发现,随着飞机飞行高度的降低,雷达可探测区域明显减小,而雷达遮蔽盲区明显增大。并且,地形遮蔽盲区的分布随方向不同存在较大差异。这是由于雷达周围不同方向的地形起伏分布差异较大引起的。从图9中在方位60°时的雷达威力探测情况可知,该方向离雷达约43km处有一处高约533m地形,这就导致了雷达在该方向上探测威力受限。因此突防飞机在突防过程中可以结合雷达遮蔽盲区的分布情况选择合理的突击方向。 图9:在60°方位雷达探测威力情况 针对不同的距离间距Δr=100m,200m,400m的情况,分别统计三个高度层的计算时间,结果如表1所示。随着距离间距的增加,计算时间随之减少,这是因为距离上的网格点相应的减少。此外,目标高度越低,越容易受雷达近区地形遮蔽的影响,计算量也会随之降低。 表1:不同距离间距下各高度层的计算时间 以上试验结果说明本文所提方法可以快速、准确地计算得到雷达的探测威力。2.2 地形遮蔽

2.3 地杂波干扰
3 高精度DEM数据下的雷达威力计算
3.1 DEM数据准备
3.2 网格划分及坐标转换

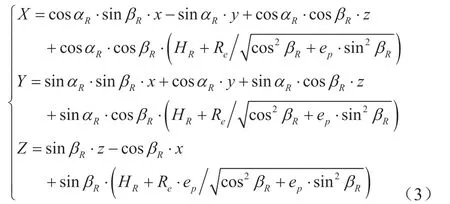
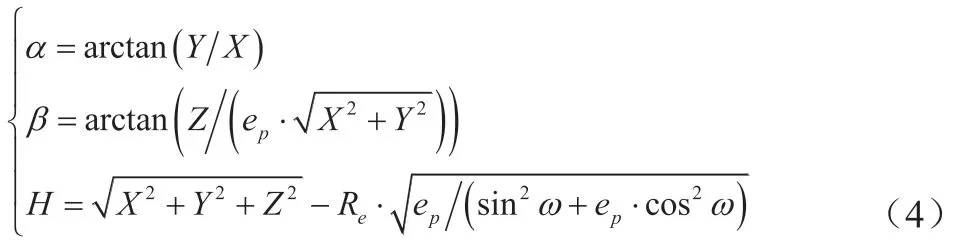
3.3 雷达威力计算


4 仿真实验