基于CMAES-LSTM的便利店SKU日销量预测方法

万忠赫 姜同强 张青川

(北京工商大学计算机与信息工程学院 北京 100048)(农产品质量安全追溯技术及应用国家工程实验室 北京 100048)(食品安全大数据技术北京市重点实验室 北京 100048)

0 引 言

随着企业管理信息化和机器学习领域的快速发展，连锁便利店行业急需基于精准销量预测的库存管理，而目前便利店销量预测还处于门店、大类粒度，粗粒度的销量预测对库存管理的作用较小，亟需实现对门店-SKU细粒度的日销量预测，优化库存促进资金周转。

传统的基于统计的销量预测方法包括：指数平滑法[1-2]、支持向量回归[3]、差分整合移动平均自回归模型[4-5]、扩散模型[6]和灰度预测模型[7-8]等，这些方法基于大量历史销售数据，在理论上对未来销量有着准确的预测，但其容易受偶然性外部因素的影响，导致准确性下降。近年来深度学习技术发展迅速[9]，深度神经网络能够从复杂的数据中提炼特征，其中LSTM(Long Short-Term Memory)凭借其“理解”上下文的记忆机制在许多序列数据预测任务中表现优异[10-12]，而LSTM网络超参数的设定能显著影响其表现，在大批量细粒度销量预测任务中，一成不变的超参数则难以保证预测精度稳定性。

综上所述，针对连锁便利店门店-SKU粒度的精准销量预测任务，本文将协变量信息引入LSTM预测模型，并通过CMAES(Covariance Matrix Adaptation Evolution Strategy)[13]对LSTM网络超参数独立调参，实现准确并且稳定的大规模销量预测。

1 时间序列特征构建

1.1 日销量时间序列

构建SKU粒度的日销量时间序列时，对于不同门店、不同SKU都需要单独构建，而每个序列的长度是不同的，因为不同的门店开业时间不同，而同一家门店的SKU因不断更迭，所以当前在售SKU的上架时间也不尽相同。设门店i∈I，SKUj∈J，其上架日期距今天数为dij，将其在x天前的日销量表示为sij，则该门店该SKU的日销量时间序列表示为:

Sij={sijdij,sijdij-1,…,sij2,sij1}

(1)

1.2 协变量特征引入

传统的统计预测方法只能使用时间序列本身，无法引入外部信息，而天气、节假日等信息对商品销量有着显著的影响。如冷饮在高温晴朗的日子更受欢迎；而在阴雨天气时虽然大部分商品销售较差，但热饮商品销量却不降反升；在学校或写字楼附近的便利店，即食盒饭在工作日一般比较畅销，而在节假日时则销量寥寥。以上例子均为外部因素直接影响着不同门店不同商品的销量，与此同时商品之间的关联性使得大量商品的销量间受到外部因素的影响，也说明了对门店-SKU粒度进行建模预测的有效性和必要性。

本文使用LSTM模型预测销量时间序列，该模型可以引入任意多个协变量，提供更加充分的商品销量相关信息，从而增强模型的预测准确性。协变量信息需覆盖销售数据中任一天有销量的日期，则有:

n=max(dij)i∈I,j∈J

(2)

温度时间序列T和空气指数时间序列A分别表示为:

T={tn,tn-1,…,t2,t1}

(3)

A={an,an-1,…,a2,a1}

(4)

天气类型包括风、云、雾、雨、雪、雷、雹、霾，该特征为定性特征，故用one hot编码进行数值表示，即生成维度等于该特征不同值个数的向量，每种特征取值在向量固定位置取值为1，其余位置取值为0，各天气类型独热码如表1所示。

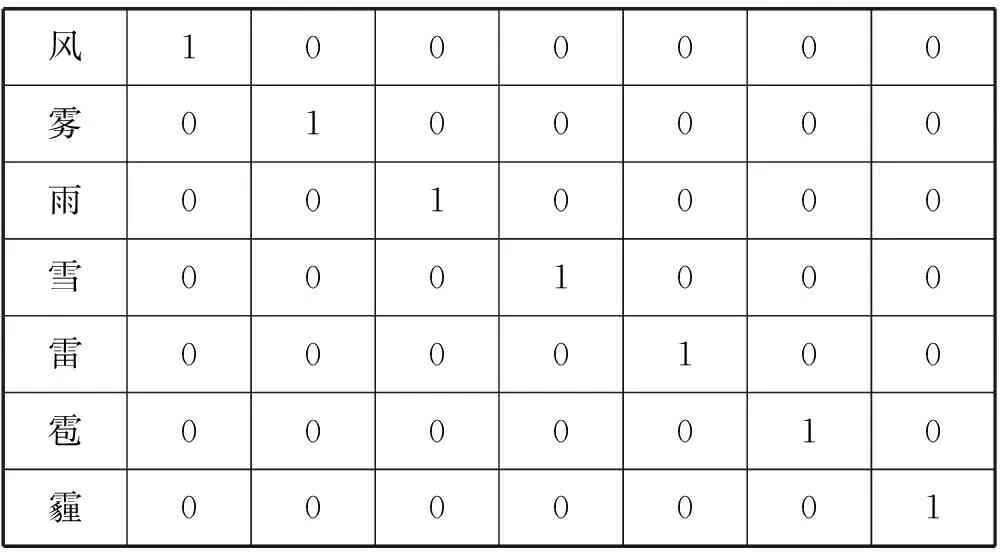
表1 天气独热码

天气类型时间序列W表示为:

W={wn,wn-1,…,w2,w1}

(5)

当x天前为工作日时hx值为0，否则为1，节假日信息时间序列H表示为:

H={hn,hn-1,…,h2,h1}

(6)

1.3 权值归一化

将协变量引入模型时，不同特征量纲会导致对模型预测结果影响的权重不同，因此需要对协变量特征值进行归一化处理，对温度时间序列T={tn,tn-1,…,t2,t1}有：

(7)

同样的，对空气指数时间序列A进行归一化处理，而天气类型时间序列W和节假日时间序列H原始值已经符合要求，取值为{0,1}，无需进行归一化处理。

2 CMAES-LSTM预测模型

2.1 LSTM模型

长短期记忆神经网络LSTM是在循环神经网络RNN的基础上发展而来，RNN按时间序列逐个输入到细胞中，并保有细胞状态，每一时刻通过当前输入值和网络权值更新细胞状态，并得到该时刻的输出，在预测问题中RNN网络为多入单出，即只取最后时刻网络的输出作为预测结果。而预测损失通过链式求导法则反向传播，从而更新网络权值。典型的RNN网络根据时序t展开如图1所示。

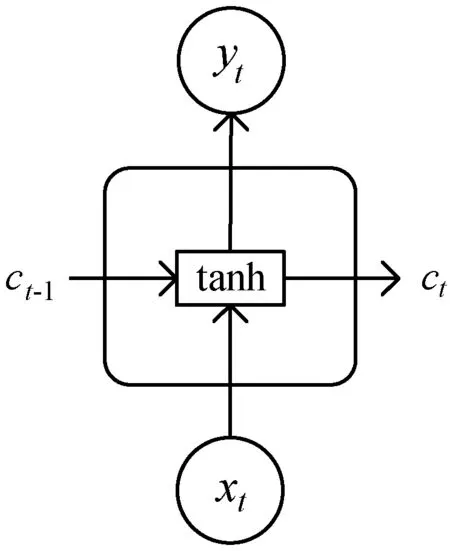
图1 循环神经网络

RNN理论上具备记忆机制，可以对输入的序列进行学习，而实际训练过程中深度过深的链式求导则会导致梯度消失或梯度爆炸的问题，这会使得RNN出现“记忆衰退”，对时序较早的信息不够敏感，丢失信息。

LSTM网络型的三重门机制避免了RNN中“记忆衰退”的问题，三重门为输入门、遗忘门和输出门，t时刻的LSTM细胞如图2所示。时间序列数据按序输入细胞中，首先遗忘门对细胞状态选择性遗忘，然后通过输入门对当前时刻输入选择性记忆，最后输出门控制细胞状态的输出。

图2 长短期记忆神经网络

具体地，LSTM细胞在t时刻需要对t-1时刻传来的细胞状态中的部分信息进行遗忘，遗忘门即一个普通的BP神经网络，通过权值和偏置对上一时刻的细胞状态和这一时刻的输入信息进行计算，并经过sigmoid函数得到与状态维度相同的向量ft，其值在[0,1]范围内，1代表对该位信息完全保留，0代表完全遗忘。

ft=σ(Wf·[ht-1,xt]+bf)

(8)

接下来输入门首先计算要将这一时刻输入的信息哪些部分写入细胞状态，与遗忘门的计算相似，同样通过sigmoid函数表示对每一维度信息的保留程度it。

it=σ(Wi·[ht-1,xt]+bi)

(9)

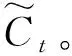
(10)

(11)

输出门的计算与输入门和遗忘门相似，对上一时刻的输入ht-1以及此刻的细胞输入xt计算后的结果进行sigmoid激活，得到对细胞状态输出的控制向量ot。

ot=σ(Wo·[ht-1,xt]+bo)

(12)

ht=ot·tanh(Ct)

(13)

2.2 模型输入样本构建

假设构建了所有门店所有SKU的日销量时间序列sij,i∈I,j∈J，以及外部特征的时间序列，分别是温度T、天气类型W、空气指数A以及节假日H。进行深度学习模型的训练和预测，需要将数据处理成feature-label对的形式。设一个样本的特征取窗口大小为p的序列，以步长r滑动窗口不断生成样本，则对于门店i的SKUj，一共能够生成Kij个样本，其中第k个样本的特征为featurek，标签为labelk。

Kij=(dij-p+r)%r-1=(dij-p)%r

(14)

(15)

labelk=sijk·r

(16)

2.3 CMAES

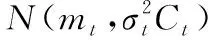
首先，在一次迭代中，从每个超参数的正态分布中取值，共产生λ个超参数组：

xi=mt+σtyi,yi～N(0,Ct)

(17)

式中：yi是通过协方差矩阵C特征分解得到的搜索方向，即：

yi=BDzi,zi～N(0,I)

(18)

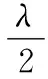
f(x1:λ)≤f(x2:λ)≤…≤f(xλ:λ)

(19)

最后使用最大似然估计的方法分别对每个超参数的分布参数mt、Ct和σt独立更新，在t+1时刻的更新表示为：

(20)

(21)

(22)

(23)

(24)

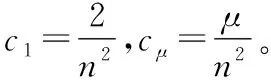
2.4 CMAES-LSTM超参数优化步骤

LSTM预测模型中，超参数的选择会对模型性能及预测结果产生影响，传统的依据经验的人工选择方法很难保证选择到最优参数，网格搜索通过穷举的方法保证选择性能最优的一组参数，但其时间复杂度是不可接受的。LSTM模型中主要的超参数及其取值范围如表2所示。

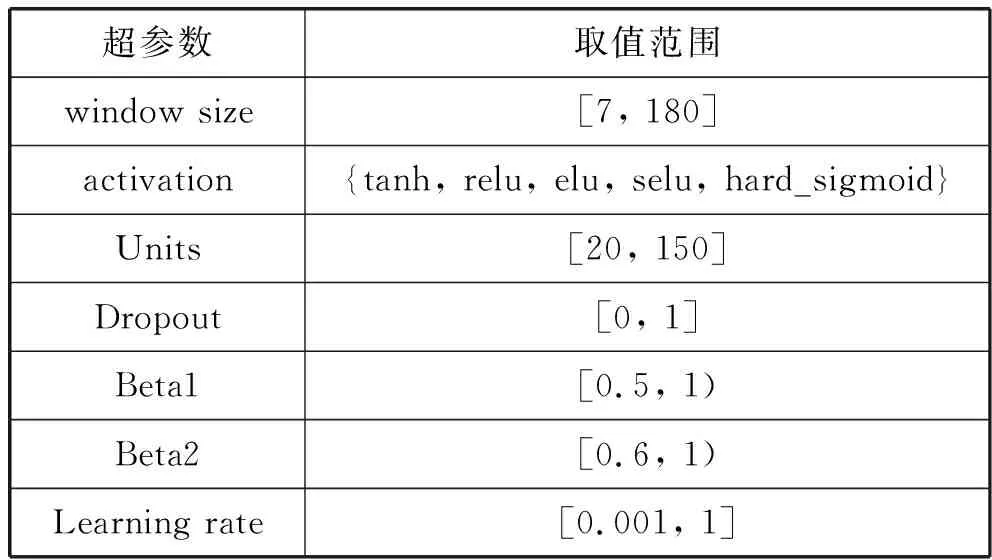
表2 超参数取值范围

其中window size表示基于时间序列构建样本时间窗口p的大小；activation表示网络输出使用的激活函数；在LSTM细胞中的三重门均为传统BP神经网络，units设置了其神经元个数；Dropout的比例表示在训练过程中以概率是神经元失效，从而使得每轮训练使用的网络结构不完全相同，提高模型鲁棒性；本文使用Adam优化器，learning rate表示其学习率，beta1和beta2为Adam优化过程中一阶和二阶据估计的指数衰减率。

通过协方差自适应调整的进化策略在LSTM超参数空间的搜索过程如图3所示。(1) 基于日销量及协变量时间序列构建样本，并划分训练验证集；(2) 输入各超参数的取值范围并初始化超参数的分布；(3) 产生λ个超参数组；(4) 计算每一个超参数组产生的LSTM模型在训练验证集上的适应度并舍弃一半的解；(5) 逐个更新超参数分布的每个参数；(6) 判断是否满足终止条件，损失函数低于阈值或达到最大迭代次数，如不满足终止条件则返回步骤(3)；(7) 取适应度最大的解作为LSTM超参数生成模型，对测试集进行预测，输出预测结果。

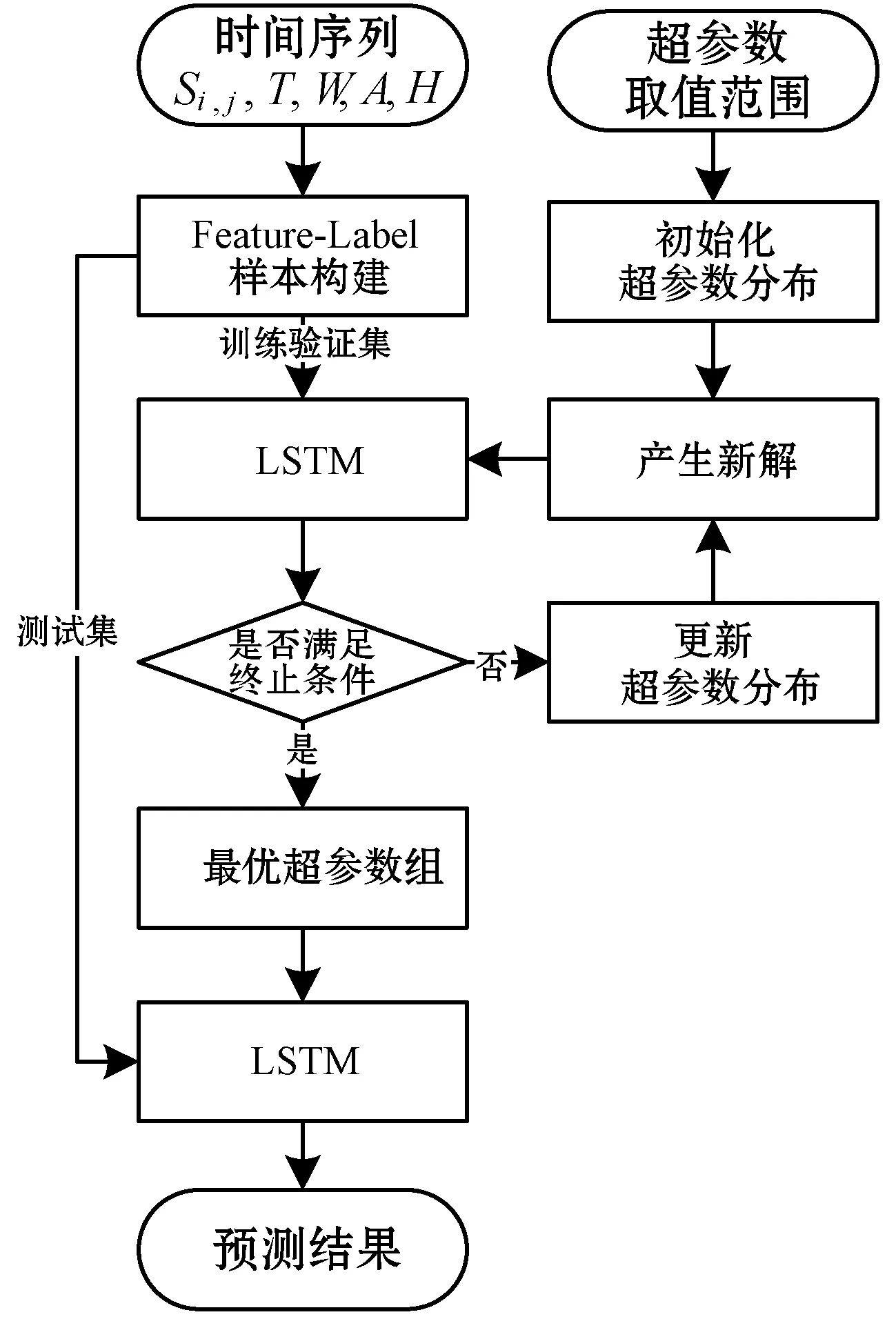
图3 CMAES-LSTM流程图

3 实验与结果分析

3.1 实验数据

数据来自某连锁便利店300家门店2018年1月至2019年12月的销售数据，每一家门店根据其地理位置有着不同的定位，包括地铁店、商务店、学校店、社区店以及景区店，便利店集团共有超过2 000个不同的SKU，覆盖13个大类，因此共有20 000余个门店i-SKUj日销量时间序列，本文对5类门店以及13个大类的SKU，等比例随机抽取共1 000个时间序列进行实验。

3.2 评价指标

(1) 平均百分比绝对误差。本文使用平均百分比绝对误差来对比不同预测算法的性能，该指标能够衡量销量预测的准确性，并且能直观地反映出预测值的准确程度。

(25)

(2) 标准差。标准差是离均差平方的算术平均数的平方根，用σ表示，标准差能反映一个数据集的离散程度。平均数相同的两组数据，标准差未必相同。

(26)

3.3 时间序列预测算法对比实验

实验对比了不同算法在1 000个门店-SKU销量预测任务的性能，平均MAPE值可以对比不同算法的整体性能，只使用日销量时间序列进行预测的评价值为MAPE-a，引入协变量时间序列得到的评价值为MAPE-b，实验结果如表3所示。

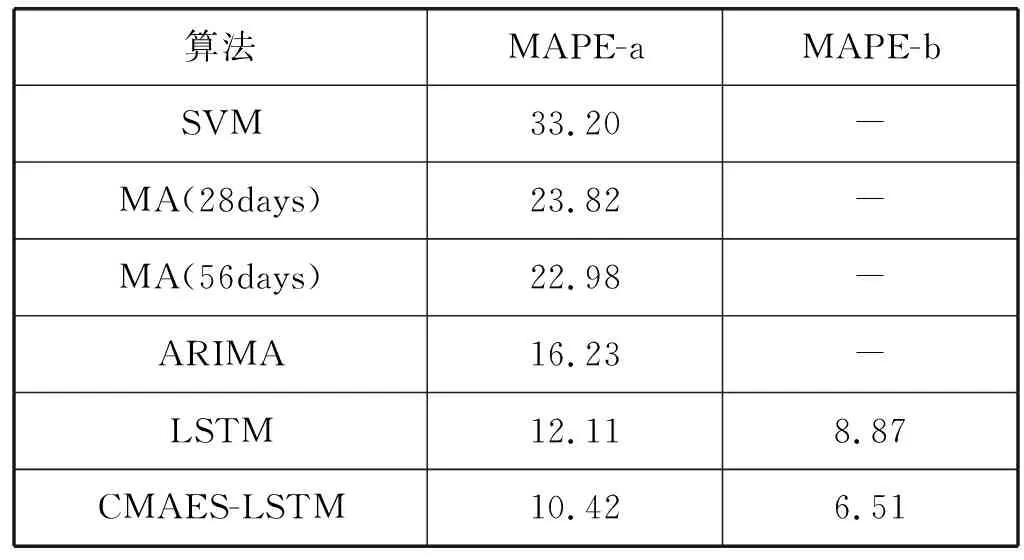
表3 MAPE值对比(%)

根据表3中的实验结果，移动平均法作为传统的时间序列预测方法，其原理简单使用广泛，一般作为时间序列预测任务的benchmark，可以发现当时间窗口从4周扩大到8周时，整体性能有提升但不显著，ARIMA在MA的基础上增加的差分，使得序列平稳，可以发现其整体性能较MA有显著提升。LSTM在本文任务表现最佳，MAPE值降至12.11%，作为深度学习算法，凭借其有效的特征抽取能力，在引入协变量信息后预测性能进一步提升。但本文任务为门店-SKU粒度的销量预测，不同门店SKU销售情况差异大且受外部因素影响的模式也不尽相同，通过CMAES对每个模型独立调参，整体性能进一步提升，并且在引入协变量后性能提升幅度相较固定参数的LSTM方法提升20.68%，验证了本文销量预测方法的有效性。

而在实际应用过程中，预测偏差较大的情况则会直接导致库存积压或不足并带来经济损失，所以算法预测性能的稳定性也是重要的参考标准，可通过计算标准差和绘制盒须图的方法进行观测。只使用日销量时间序列进行预测的评价值为sigma-a，引入协变量时间序列得到的评价值为sigma-b，标准差计算结果如表4所示，盒须图如图4所示。

表4 标准差值对比

图4 盒须图

根据表4及图4的实验结果可以发现，SVM预测结果方差大，盒须图中离群点较多，其稳定性较差。移动平均法通过扩大时间窗口预测稳定性略有提升，MAPE值下限有所提升，而加入方差平稳序列后，ARIMA预测结果方差降低不明显，但从盒须图中可以发现其最远离群点位置明显下降，稳定性有一定的提升。本文方法CMAES-LSTM相对于固定超参数的LSTM模型，预测方差显著降低，盒须图中离群点位置下降明显，且1/4和3/4分位数差值减小，表明其预测稳定性更高。

4 结 语

本文针对连锁便利店的门店-SKU粒度日销量预测任务，提出引入协变量的CMAES-LSTM时间序列预测方法，得到以下结论。

(1) 由于LSTM能够对输入信息进行深度特征提取，因此在引入外部信息后预测准确性有了较大提升。

(2) 对于不同门店-SKU的时间序列，其场景不同、属性不同，使用超参数固定的LSTM模型预测整体性能较差且稳定性不足，使用进化策略独立调参，能够明显提升其预测的准确性。

在未来的工作中，可以引入更加丰富的协变量，获取更多影响销售的外部信息输入模型，提高预测性能；还可以将销售记录与用户关联，通过用户画像等方法，使用对人的购买意向的预测来影响销量预测。