基于CNN的低信噪比多载波测控信号调制识别算法

杨亮亮

（中国西南电子技术研究所 四川省成都市 610036）

1 引言

测控（遥测遥控）系统在无人机、导弹、航天器的发射和应用中占有极其重要的地位。侦收测控信号是获取空间高速目标信息的重要手段，在现代电子战中的角色也越来越重要，是电子侦察对抗中的重点任务。通过对遥控遥测信号进行跟踪侦收，一方面可以发现确认目标、收集信号样本，另一方面可以支撑引导对抗干扰。

测控系统一般采用较复杂的复合调制形式，常用调制信号有BPSK-FM、BPSK-PM、QPSK-FM、QPSK-PM，与BPSK、QPSK、OQPSK等之间具有相似性，识别分类具有模糊性。因此在大范围参数、低信噪比条件下提升多载波复合调制信号的识别能力具有重要研究意义。

信号调制样式的识别一般都是基于判决理论、统计模式以及深度学习三个方面进行实现，目前对复合调制信号的自动识别已有相关研究。文献采用基于判决理论的识别方法，根据瞬时频率直方图区分载波FM和PM调制，再利用相应特征参数对副载波调制样式PSK、FSK等进行判决识别，理论完善、步骤简单，具有很好的效果，但需较多的先验知识，适用于特定模型环境。文献采用统计模式的识别方法，对常规和复合调制信号采用不同方法，复合调制信号先进行内外调制分离识别，结合频谱幅度的紧致性特征和瞬时相位功率谱特征进行内外层调制识别，验证表明PM复合类调制信号的识别性能较好，但FM复合类调制信号，由于噪声影响识别效果较差。基于深度学习的识别方法目前大多针对常规调制信号，复合调制信号较少。

本文采用基于深度学习的设计思路。针对常用的载波测控信号调制样式，设计卷积神经网络，提取训练数据库中信号的一阶、二阶、四阶循环谱特征进行学习训练，循环谱不仅可以表征信号自身频谱特性，还可表征信号周期性特征，包括隐藏在噪声中的弱周期性，而且多阶循环谱特征有利于区分复合信号BPSK-FM、BPSK-PM、QPSK-FM、QPSKPM及BPSK、QPSK相似性，避免分类的模糊性。另外，提出了利用自身高频方差作为参考，动态调制阈值的小波阈值算法，设计阈值求取公式，将待识别的未知信号进行降噪处理后输入到训练好的模型中实现调制样式的自动识别，提升低信噪比条件下的识别概率。

2 多载波测控信号循环谱特征

2.1 循环谱理论及算法

循环谱及相关理论分析信号时，不仅能够解析出信号的一阶周期性，还能解析出高阶周期性及隐藏在噪声中的弱周期性，并利用信号的自相关性来抑制噪声，具有良好的抗噪声性能。

假设随机信号为x(t)，如果其均值为M(t)=E(x(t))为周期函数，相关函数展开傅里叶级数的系数为：

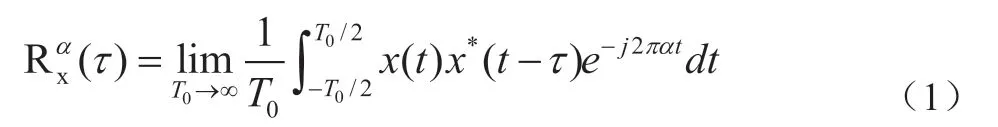
为循环谱密度函数，也称为循环谱。

调制信号虽是非平稳过程，但其统计特性呈周期或多周期规律变化，为循环平稳过程。循环谱的工程计算方法有很多种，工程实现可采用计算量小的SSCA算法，其在损失一定性能的条件下能够大幅度降低运算量。

2.2 多载波测控信号循环谱分析

多载波测控信号的循环平稳特性与符号速率、载波频率、副载波频率、失真等因素相关，利用循环谱特征，可以寻找不同调制信号特征差异，实现调制样式的识别。循环谱谱峰含有丰富的信号参数比如载频、码元速率等特征信息，同时谱峰位置以及峰值大小均能体现很多特征。

以复合调制PCM/BPSK/FM信号为例，信号循环自相关性函数只与每项自相关有关，推导可得s(t)的谱密度函数为：

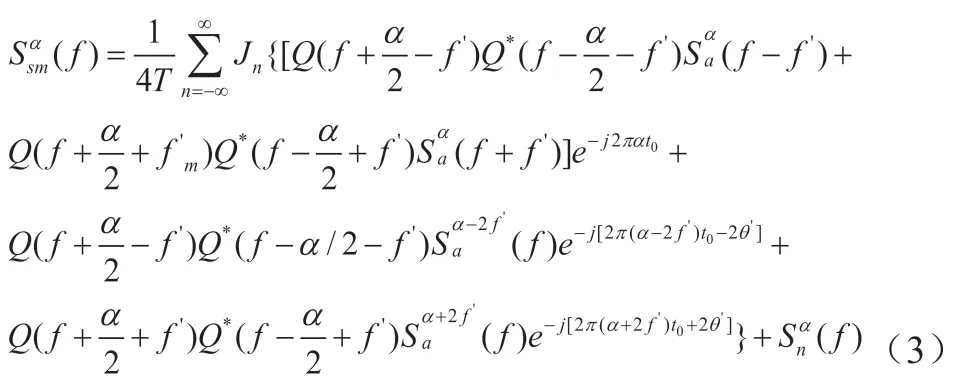
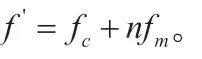
3 小波降噪

3.1 小波分析理论基础

小波是在定义域为有限长、期望为零的波形，小波变换即为信号与小波基函数的卷积处理，改变小波基函数的时间和尺度两个参数可实现对目标信号的局部时频分析，相比短时傅里叶变换，小波变换能够克服由时间分割造成的频率特性损失。小波变换也可看做是信号通过冲击响应为小波基函数的带通滤波器组的滤波，滤波器的中心频率和带宽随尺度变化而变化。小波变换具有很好的时频分析能力，但运算复杂，Mallat算法能够极大减少计算量，实现工程应用。利用滤波器H、G获取层数不同的小波系数，各层计算公式为：

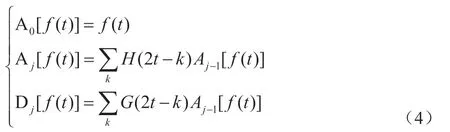
t为时间，f(t)为输入原始信号，j为分解层数，H为低通分界滤波器，G为高通分界滤波器，A为j层小波系数低频部分，D为j层小波系数高频部分。

3.2 小波阈值降噪设计

测控信号长距离传输过程中会有较大衰减，同时容易受噪声干扰，降噪处理能够有效提升对低信噪比信号的识别概率。噪声信号在空间和时间上一般为离散状态，小波系数较小，有效信号一般呈连续状态，小波系数较大，所以在Mallat算法获取层数不同的小波系数后，可对其进行阈值处理，最后再利用重构滤波器恢复出有效信号。步骤如下：

步骤1：选择合适小波基，变换得到小波系数；

步骤2：设置阈值，确定阈值函数；

步骤3：根据阈值进行小波系数分离处理；

步骤4：小波逆变换，合成降噪后的信号；

小波基选择：小波母函数多种多样，针对信号特征以及数字离散处理的可行性，可在小波基Symlets、Daubechies中进行选择，通过仿真实验，在条件都一致的情况下，小波函数Daubechies具备最优降噪效果。

分解层数选择：分层越多降噪效果越好但计算量也越大，需权衡两者选择合适分解层数，通过仿真分析，三层分解即可有效降低噪声影响，图1为加噪BPSK/FM调制信号小波分解每层低频分量与高频分量图。

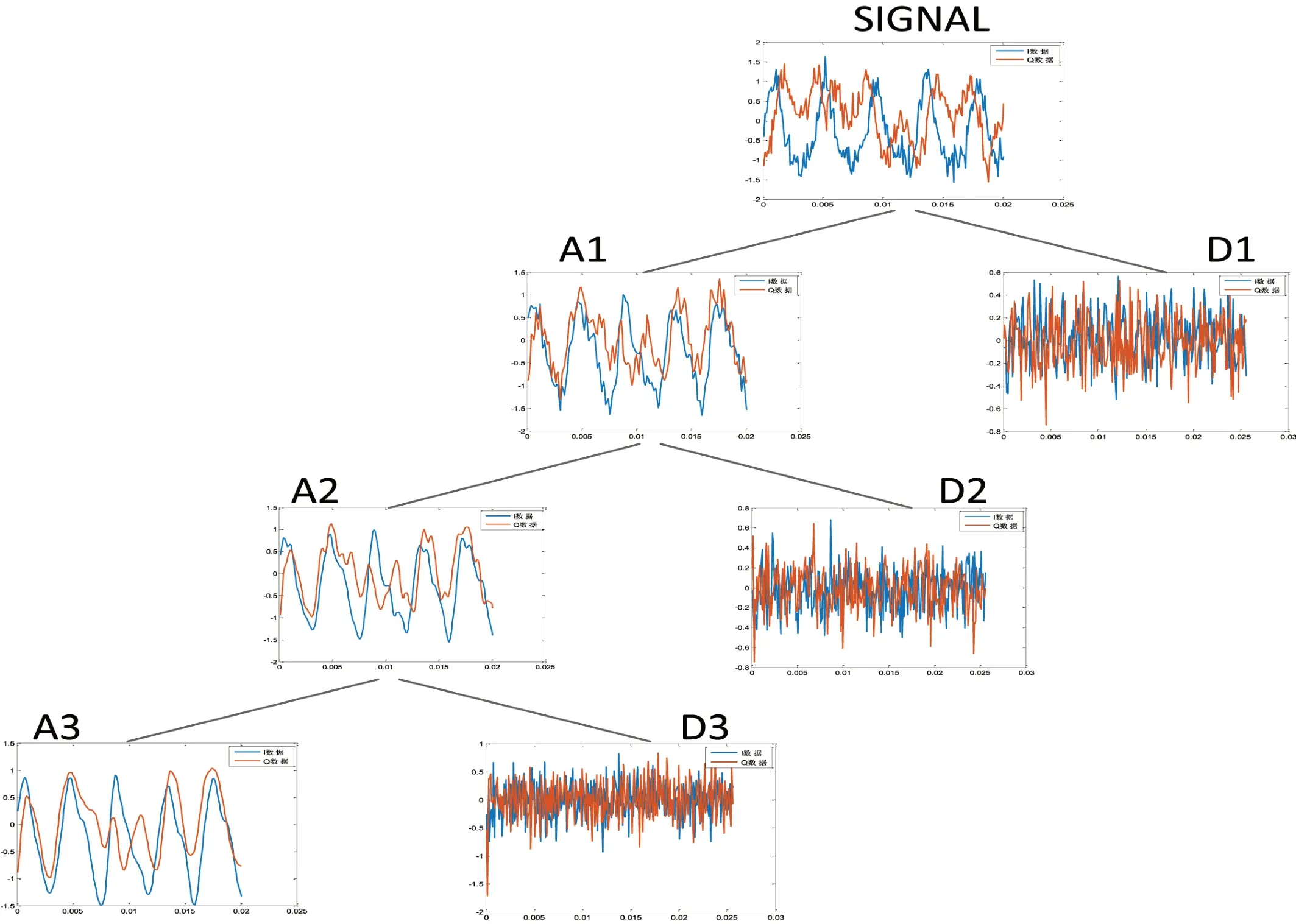
图1：加噪BPSK/FM调制信号小波分解

鉴于信号和噪声具有明显差异，为便于工程实现，选用硬阈值处理，小于阈值的小波系数（噪声产生）置零，保留大于阈值的小波系数，阈值函数：

式中ω为小波系数，T为硬阈值系数。

阈值系数设计：硬阈值T的设定至关重要，过小不能降低噪声，过大则会过多抑制有用信号，造成失真。另外，不同环境、不同调制信号均会不同，所以阈值T必须从信号自身提取。结合经典的阈值计算公式，采用分层阈值方法，用第一层高频系数作为方差参考值，计算公式：

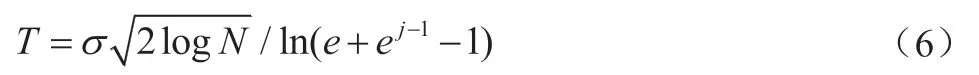
式中，σ为分解第一层小波分解高频系数，N为信号长度，j为小波分解层数。图 2为BPSK/FM加噪信号去噪前后信号IQ数据对比图。

图2：去噪前后信号IQ对比

图3：算法框图

4 基于CNN架构的调制识别算法

4.1 卷积神经网络（CNN）基础

卷积神经网络在传统多层神经网络的基础上发展而来，增加了更为有效的特征学习，主要是在全连接的基础上增加了部分连接的卷积层和池化层，使得学习的网络层数加深，学习能力加强。

卷积神经网络主要有输入层、卷积与池化层、全连接层。输入层进行去均值和归一化处理，规范输入数据的完整性。卷积和池化层主要完成特征工程，卷积层提取输入数据的局部特征，后级层网络从前级特征中迭代提取更为复杂特征，池化层也叫下采样层，通过压缩数据参数，降低网络复杂度。全连接层也为输出层，起到分类回归的作用。

4.2 算法及框架设计

算法分为训练过程和识别过程两部分。训练过程是针对训练库的数据进行自动学习提取特征的过程，识别过程则是对未知信号通过已经训练好的模型进行类型判别的过程，整体算法框架如图 3。

训练过程针对已知调制类型信号进行特征自动提取学习。为了能准确识别信号，需采集大量已知调制方式信号组建全面的高质量训练数据库，同时为了使训练模型具备泛化能力，训练信号的载波和码速率组合须全部覆盖。为更多维度表征信号特征，提取一阶、二阶、四阶循环谱作为训练输入，并通过图像化处理形成标准训练图像。训练过程是一个不断调整CNN架构的过程，通过对提取的样本数据库进行学习训练，不断的迭代调整架构参数，使得识别误差达到或者趋于理想值，最终获取最优模型。

识别过程采用已训练好的模型对未知信号进行调制识别。依据循环谱特征理论，噪声及干扰不具备周期循环平稳特点，在循环频率为零（α=0）平面上表征噪声及干扰自身特征，在循环频率非零（α≠0）噪声干扰为零，但这是在检测数据连续且开窗无限长度的前提下，而实际工程中，信号的分析长度都是有限的且离散的，在α≠0平面仍然会出现噪声残留，及噪声会影响信号循环谱的表征，尤其是低信噪比信号。结合小波降噪处理方法，首先将采集的未知信号进行降噪处理，然后再计算循环谱，图像化处理后形成标准图片，输入到训练后的神经网络进行识别判断，最后输出识别结果。

4.3 卷积神经网络设计

卷积网络采用共10层共28级的架构。第一层为输入层，输入维度33x4097x3，循环频域33个像素点，信号频率4097个像素点，即一阶、二阶、四阶三组循环谱图像化处理后输入。中间包含6层共24级的卷积池化处理，每层卷积核大小均采用3x3大小，激活层函数选用ReLU函数，前5层均采用最大池化方式，第六层采用平均池化方式。最后为全连接层及输出层，激励函数选择softmax函数。具体网络架构如表1。

表1：卷积神经网络架构

5 试验及结果

采集训练数据库进行训练，经过多次的迭代训练，验证准确度及损失值趋于收敛，如图 4。

图4：训练过程图

采用验证数据进行验证，不同信噪比下进行识别，识别概率如图5、图6，信噪比在10dB情况下能够精确识别各调制样式，当信噪比将为3dB时，识别概率下降。

图5：SNR=10dB识别概率

图6：SNR=3dB识别概率

6 结论

为自动识别低信噪比条件下多载波复合调制测控信号的调制样式，本文分析其循环谱特点，设计卷积神经网络架构，对信号循环谱图像化后进行迭代学习，自动提取各调试样式特征，获取识别模型；同时设计小波阈值降噪算法，阈值依据信号自身方差动态计算，对未知信号进行降噪处理后，计算循环谱输入到训练好的模型中，实现调制样式的自动识别。通过试验验证，该方法不仅能够自动识别出多载波测控信号的复合调制样式，且能有效降低噪声干扰影响，提升低信噪比条件下的识别性能。