基于自适应EKF-AHI的锂电池SOC加权估计

张帅帅 毕恺韬 颜文旭 倪宏宇 储杰

摘  要：为了更准确估计锂电池的SOC，从两方面考虑，即模型选择和估计算法。首先，为了减小由于模型引起的估计误差，采用带有遗忘因子的递推最小二乘法对二阶RC等效电路模型参数进行在线辨识，实现锂电池模型参数的自适应。其次，针对SOC的估计，提出了基于EKF结合AHI法实现加权在线估计。实验表明所提方法相比其中单一算法具有更高的估计精度和稳定性，尤其是提高了低SOC区间的估计精度，验证了所提算法的有效性。

关键词：SOC估计;在线参数辨识;EKF;AHI;加权算法

中图分类号：TM912         文献标识码：A文章编号：2096-4706（2022）04-0048-06

Lithium Battery SOC Weighting Estimation Based on Adaptive EKF-AHI

ZHANG Shuaishuai1， BI Kaitao1， YAN Wenxu1， NI Hongyu2， CHU Jie2

（1.School of Internet of Things Engineering， Jiangnan University， Wuxi  214122， China; 2.State Grid Shaoxing Power Supply Company， Shaoxing  312000， China）

Abstract： In order to estimate the SOC of lithium battery more accurately， this paper considers two aspects： model selection and estimation algorithm. Firstly， in order to reduce the estimation error caused by the model， the recursive least square method with forgetting factor is used to identify online the second-order RC equivalent circuit model parameters， so as to realize the self-adaptive of the lithium battery model parameter. Secondly， for SOC estimation， a weighting online estimation based on EKF and AHI is proposed. Experiments show that the proposed method has higher estimation accuracy and stability than the single algorithm， especially the estimation accuracy of low SOC interval， and verifies the effectiveness of the proposed algorithm.

Keywords： SOC estimation; online parameter identification; EKF; AHI; weighting algorithm

0  引  言

由于锂电池相较于其他类型电池具有能量密度高、使用寿命长、绿色环保等优点[1]，目前作为主要的动力源和储能单元已广泛应用于多个领域。因此，为了更好地优化电池管理系统（Battery Management System， BMS）[2]，保证电池使用的安全性和可靠性是非常有必要的。BMS的难点之一是SOC的估计[3，4]。SOC的精度直接对系统的安全管理、决策和均衡控制等起到决定性作用。

影响SOC的估计精度主要来自模型选择和估计算法。首先，针对模型的选择，文献[5-7]给出了目前锂电池估计SOC时常用的几种等效电路模型，比如RINT模型、n阶RC模型、GNL模型和PNGV模型等，像GNL模型、PNGV模型等一些改进的等效电路模型复杂，估计精度高，但是算法计算量比较大，不太适用于工程实践中。针对SOC的估计，常见的方法有开路电压（Open Circuit Voltage， OCV）法[8]、安时积分法（Ampere Hour Integral， AHI）[9]、卡尔曼滤波系列算法[10-13]和人神经网络法[14]等。AHI法和OCV法是最简单的方法，复杂度低。但是AHI法因为存在积分环节导致误差无法消除且随时间推移会逐渐增大;而OCV法需要电池进行长时间静置提前获悉SOC-OCV关系且受多方面影响，不适用于汽车的实时在线估计;卡尔曼滤波系列算法可以利用噪声传感器使系统的均方根估计误差降低，但是对建模精度要求较高，并且卡尔曼系列算法目前大都无法解决在低SOC区间下误差不可控的情况;神经网络算法虽然精度较高，但计算量大且耗时长。因此在选择模型和SOC估计算法时都要考虑估计精度与复杂度。

为此，本文首先用带有遗忘因子的递推最小二乘法（Forgetting Factor Recursive Least Squares， FFRLS）對模型进行在线参数辨识，实现模型参数的动态更新，以减小由参数辨识引起的估计误差;然后将辨识出来的模型参数作为输入，通过基于扩展卡尔曼滤波（Extended Kalman Filter， EKF）算法结合AHI法的加权实时估计SOC，充分利用两种算法的优点来提高SOC的估计精度，既可以解决AHI法因为积分环节导致误差累积的天然弊端，也有效解决了EKF在线性化时忽略高阶项所引起估计误差的局限性和严重依赖于电池模型的问题，有效提高了整个SOC区间的估计精度，尤其降低了在低SOC区间下的误差。DCD84A21-20B9-4127-8F37-916BA023FC35

1  锂电池建模和参数估计

1.1  锂电池等效电路模型

等效电路模型是SOC估计中最常用的模型，这主要因为能够良好反应电池充放电特性、结构简单和运算复杂度低。因此，本文采用二阶RC模型，即由一个内阻和两个RC环构成，如图1所示。

图1中：Ut为电池端电压;UOCV为开路电压，它与SOC有一定關系;I为充放电电流（充电为正，放电为负）;R0 为电池内阻，两个RC环用来表征电池内部发生的极化效应，此模型能较好地模拟电池的动态响应特性。

根据图1所示的等效电路模型可以得到电池各状态参数之间的关系：

式中，U1和U2分别为RC环上的电压。

1.2  SOC-OCV特性曲线

SOC反映了电池当前时刻的电量与额定电量之比。常用安时积分方程为：

式中，SOC（0）为电池初始状态下的SOC值;Cb为电池的额定容量;t表示采样时间;I（t）表示充放电电流。

在进行电池模型参数辨识及SOC的估计过程中，还需要提前测取OCV与SOC关系曲线。本文利用静置法来获取，并将得到实验数据如表1所示。

将表1收集好的数据利用多项式拟合函数Polyfit进行函数拟合，七阶效果较好，符合实际情况，拟合结果曲线，如图2所示，对应的SOC与OCV之间的拟合函数关系为：

Uocv（SOC）=99.6SCC7-399.8SCC8+470.5SCC5

-342.5SCC4+141SCC3-32.1SCC2

+4.19SCC+3.324（3）

1.3  模型参数辨识

由于锂电池在充放电过程的内部化学反应较为复杂，模型参数易受多个因素影响，因此为了排除由于模型参数造成SOC的估计误差，并实现模型参数的自适应，需要对模型参数在线辨识并做出实时修正。

本文采用FFRLS方法来实时辨识并更新模型参数（R0，R1，C1，R2，C2），此方法是基于递推最小二乘（Recursive Least Squares， RLS）法的一种改进方法。可以有效解决RLS算法中由于数据量过大而造成“数据饱和”问题[15]。

FFRLS算法按式（4）推导得到：

式中，是上一时刻估计值;y（k+1）是系统测量值;y（k+1）-ΦT（k+1）是预测误差;K（k+1）为增益;E为单位矩阵;λ为遗忘因子，取0.95～1。

将电池模型转换成可应用于FFRLS算法的数学形式。由图1的电池模型可得：

其中时间常数τ1=R1C1，τ2=R2C2;

令

将式（5）离散化后，整理可得：

其中：

式中T为采样时间，即可将式（8）代入FFRLS的辨识方法中，其中：

其中θ是FFRLS算法中的直接辨识参数﹐模型参数再由θ推导而出。

令k0=T2+bT+a，可以推出：

至此，式（10）即是等效电路模型中所有参数的估计值。

2  联合估计算法

2.1  EKF算法

卡尔曼滤波系列算法本质上是一种最小方差的估计算法。其核心思想是：利用上一时刻的状态估计值和当前时刻的观测值来求得当前时刻的状态估计值，同时更新状态变量[16]。标准卡尔曼滤波只适用于线性系统，但是由式（3）可以看出UOCV（SOC，k）是一个非线性函数，对于非线性系统，本文采用EKF算法。

设锂电池非线性模型的状态和观测方程为：

x（k+1）=f[x（k），u（k）]+W（k） （11）

y（k）=g[x（k），u（k）]+V（k） （12）

分别将系统中的非线性函数f [x（k），u（k）]和g[x（k），u（k）]线性化，得到近似线性化状态空间方程：

x（k+1）≈A（k）x（k）+B（k）u（k）+W（k）  （13）

y（k）≈C（k）x（k）+Y（k+1）+V（k）（14）

其中：

然后利用基本线性卡尔曼滤波的方法进行计算。计算公式为：

在使用EKF算法之前，要将式（1）和式（2）进行离散化，得到离散化的状态方程和输出方程，如式（17）～式（18）：

Ut（k）=Uocv（SOC，k）+U1（k）+U2（k）+I（k）R0（18）

式（17）和式（18）已经建立了电池模型的状态空间表达式，对状态空间表达式进行线性化处理。得到A（k），B（k）和C（k）分别为：

然后利用式（16）进行EKF的递推运算。从公式（17）和（18）看出，EKF算法本质上其实还是基于OCV法去估计SOC;其步骤是先利用AHI法得到SOC的初值，然后通过辨识出来的等效电路模型参数计算出电池的端电压，并和观测出来的端电压之间的误差作为校正SOC的依据;同时，状态和观测方程中的W和V还考虑了噪声和误差的影响，通过计算出每次迭代的滤波增益k（k），从而得到SOC的最优估计。

2.2  EKF-AHI加权算法

由图2的SOC-OCV曲线可以观察到，基于开路电压法的EKF算法在SOC特定区间里（例如SOC在0.2～0.5和0.7～0.9区间）时，斜率较小，即SOC对OCV的微小变化过于敏感，由于EKF算法本质上是基于OCV法去估计SOC，在此区间内难以准确估算SOC，容易造成误差。

此外，基于二阶RC的等效模型的SOC估计算法还有一个弊端，从公式（16）（17）可以看到EKF算法对非线性函数使用泰勒展开式进行一阶线性化时，忽略了其余的高阶项，从而导致了由于线性化所引起的估计误差，会使滤波发散，具体会表现在EKFS算法在估计SOC时，会始终与参考值保持一定的误差且无法单独消除，其误差根源就在于忽略的高阶项，这种误差在SOC较高时，所占比值可以当作估计误差忽略不计;但是在低SOC区间时，虽然SOC估计误差本身并没有发生明显变化，但所占比值会因SOC逐渐降低而增大，这是EKF算法本身存在的局限性。因此EKF算法是最小方差准则下的次优滤波器，其性能依赖于局部非线性度。DCD84A21-20B9-4127-8F37-916BA023FC35

综合以上分析，为了降低误差，提高SOC的估计精度，尤其是低SOC区间的精度，本文增加AHI法作为基于OCV法的EKF算法的一种辅助算法，两种算法通过加权的方式进行融合。算法流程图如图3所示。

图3中，SOCEKF和WEKF分别代表着主要算法EKF所估算出的SOC和所代表算法的权重大小，SOCAHI和WAHI代表着辅助的AHI法估算出的SOC和權重大小，两种算法的权重之和应为1。权重分配法则依据SOC-OCV分段线性曲线中每段的斜率进行权重分配，表2为各个SOC线段区间的斜率。因为EKF算法本质上是基于OCV法改进而来，斜率的大小和主要算法EKF所估算出来的SOC权重成正相关，和辅助算法AHI法所估算SOC的权重呈负相关，即斜率较大时，则表明更多的是依靠EKF算法所估计的SOC，说明EKF算法所估计的SOC越精确。相反时，则表明更多的是依靠AHI法所估算SOC，说明AHI法越精确。

实时权重分配根据前一时刻所联合估算的SOC值进行分配，这样就实现了SOC的闭环估计。表2为具体权重分配图，具体的分配规则为：WEKF的权重为当前EKF算法估计的SOC值所对应的SOC-OCV曲线各个线段斜率与线段最大斜率之比，两种算法权重的大小代表了该种算法所估算SOC值的可信程度。

最终获得的SOC估算结果为：

SOC=WEKF×SOCEKF+WAHI×SOCAHI（19）

至此，式（19）把两种算法巧妙地结合起来，一方面利用EKF算法作为主要算法去估计SOC，另一方面增加AHI法作为辅助算法去修正SOC，然后利用SOC-OCV曲线斜率作为权重分配的依据，接着通过加权的方式联合估算SOC，最后通过加权算法将所估计的SOC进一步返回迭代，实现了SOC的闭环估计。该联合算法不仅融合了基于OCV法的EKF算法和AHI法各自的优点，还能克服AHI法由于存在积分环节导致误差持续增大的缺点，此外，还有效解决了EKF算法严重依赖于模型参数导致在某些特定SOC区间情况下误差不可控和线性化变换中忽略了高阶项所引起误差的弊端，能够得到较好的估算结果。

3  实验验证与分析

为了验证上述算法的可靠性，本次实验数据所使用UDDS工况，所采用的锂电池标称电压为3.6 V，充电和放电截止电压分别为4.2 V和3.2 V，最大充电电流为40 A，最大放电电流为60 A，容量为33 Ah。图4即为UDDS工况下的电流变化示意图，采样时间为1 s，共采集18 000个数据。

3.1  FFRLS在线参数辨识

图5（a）和图5（b）为FFRLS算法在线辨识五个参数（R0，R1，C1，R2，C2）的结果。

在UDDS工况下，辨识刚开始阶段，各个电池参数都有一些剧烈的变化，这可能是参数初始化存在较大偏差所导致的，但是随着FFRLS算法的作用，各参数值逐渐趋于稳定。因此，由图5可知，即使给定初值不准确，FFRLS算法也能及时修正各个参数，使参数快速收敛到真实值附近并保持稳定。根据UDDS工况数据实时迭代更新五个参数，这样就可以把图1所示原本静态的二阶RC模型动态化，将电池模型转变为时变系统，从而实现电池模型参数的自适应，有利于提高SOC的估计精度。

3.2  SOC联合估计

图6（a）和图6（b）为二阶RC等效电路模型在UDDS工况下EKF算法所估计的端电压和端电压参考值之间的比较。从这两张图可以看出，EKF算法所估计的端电压趋势均与参考值相似，误差精度较小，误差范围在-0.025～0.021 V，说明EKF算法稳定性较好，跟踪精度也很高，验证了所提模型的高精度性和稳定性。

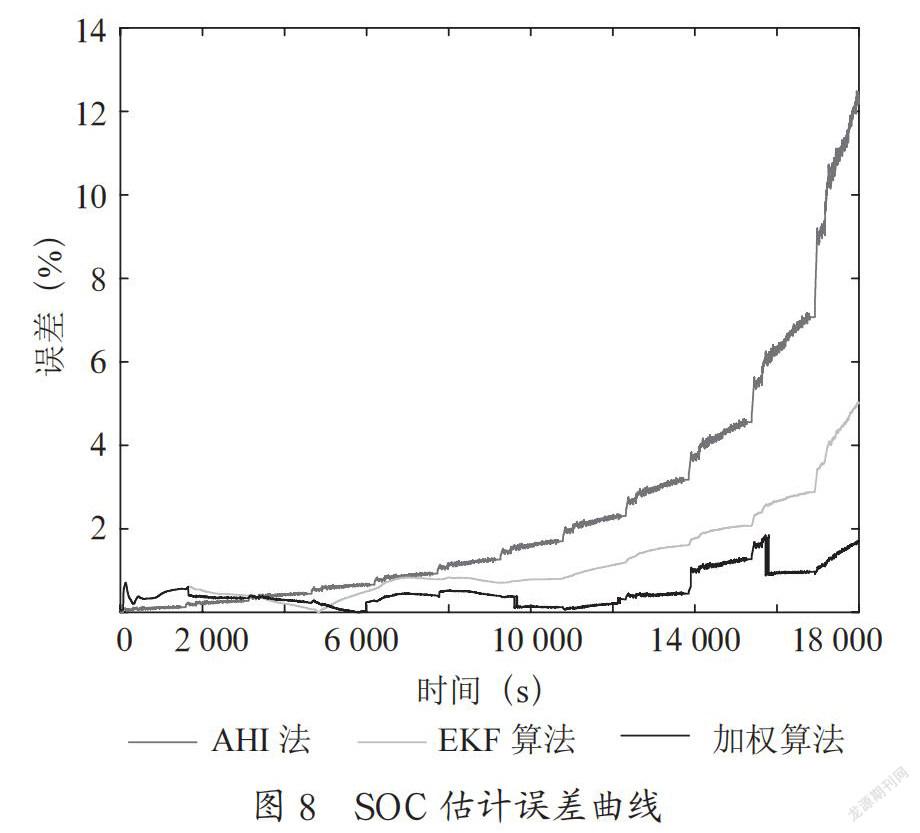
在UDDS工况下，利用3.1节中所辨识的参数，使用EKF算法计算锂电池SOC，并结合AHI法进行加权，然后与SOC参考值、AHI法和EKF算法进行比较，如图7和图8所示。图7为各个算法的估计曲线，图8为SOC估计误差。

从图中可以看出：所有算法在SOC比较高的时候（50%～100%），即使是AHI法也都有着不错的性能，误差都在2%以内，但是随着放电时间的增长，AHI法由于存在积分环节，误差逐渐增大，最大误差甚至超过12%;而EKF算法相较于AHI法能一直保持较高的精度。但是在SOC较低时（0～30%），虽然误差绝对值并没有增加多少，但是由于SOC参考值减小，导致误差百分比迅速增大，使SOC估计出现较大误差，最大误差甚至超过5%。这是由于二阶RC模型本身存在的问题和EKF算法存在弊端。因此，使用单一算法无法解决;此外，在仿真过程中发现：SOC参考值在较低时始终处在AHI法和EKF算法估计值之间，根据这一发现，本文提出一种加权估计算法，将AHI法和EKF算法估计结果进行加权，使SOC估计值尽量跟随参考值，尤其在低SOC区间，误差得到显著减小。仿真结果表明：加权算法所估计的SOC曲线较为光滑、平稳，说明稳定性比较好，即使SOC较低时，最大误差也在2%以内，说明误差精度很小。

为了比较三种算法（AHI法、EKF算法和加权算法）估计SOC的误差精度，本文采用三个数学指标来评估观测器性能：SOC实验参考值和估计值之间的均方根误差（Root Mean Square Error， RMSE）、最大绝对误差（Maximum Absolute Error， MAE）[17]和平均绝对误差（Mean Absolute Deviation， MAD），定义为：

（20）

MAE=max丨y*-y丨 （21）

（22）

式中，y*为估计值;y为参考值;N为样本个数。

表3为各个算法估计SOC的RMSE、MAE和MAD对比情况。从表3分析可知，在UDDS工况下，加权算法在整个SOC区间明显优于EKF算法和AHI法，尤其是在SOC较低时，也能有效地跟随参考值。最大绝对误差仅为1.85%，平均绝对误差和均方根误差均小于0.5%。因此，本文提出EKF和AHI法联合加权算法优于其中任何单个算法。DCD84A21-20B9-4127-8F37-916BA023FC35

4  结  论

为了能够更准确地估计锂电池SOC，提高SOC估计的精度。本文先通过FFRLS对二阶RC模型进行实时参数辨识，然后将辨识出来的参数作为输入，再联合EKF算法和AHI法去估计锂电池SOC，在UDDS工况进行分析对比，得到以下结论：

（1）基于FFRLS算法的参数辨识能够准确实时地获取锂电池二阶RC模型参数，避免了模型参数不精确引起的误差。

（2）EKF算法联合AHI法相比单一EKF算法或者AHI法能够很好地预测锂电池的SOC。尤其在较低SOC区间时，依然能够准确估计SOC，使最大绝对误差仅在2%以内，远远小于AHI法的12%和EKF算法的5%;平均绝对误差和均方根误差更是小于0.5%;能够快速、稳定地纠正给定值，更精确地估计出锂电池的SOC。

综上分析，EKF算法联合AHI法比单一EKF算法或者AHI法更适合于锂电池SOC的预测。

参考文献：

[1] LI Z，HUANG J，LIAW B Y，et al. On state-of-charge determination for lithium-ion battery [J].Journal of Power Sources，2017，348：281-301.

[2] 彭思敏.电池储能系统及其在风—储孤网中的运行与控制 [D].上海：上海交通大学，2013.

[3] PARTOVIBAKHSH M，LIU G J. An Adaptive Unscented Kalman Filtering Approach for Online Estimation of Model Parameters and State-of-Charge of Lithium-Ion Batteries for Autonomous Mobile Robots [J].IEEE Transactions on Control Systems Technology，2015，23（1）：357-363.

[4] 罗志亮.锂电池荷电状态自适应估计算法研究 [D].哈尔滨：哈尔滨工业大学，2016.

[5] CACCIATO M，NOBILE G，SCARCELLA G，et al. Real-time model-based estimation of SOC and SOH for energy storage systems [C]//2015 IEEE 6th International Symposium on Power Electronics for Distributed Generation Systems （PEDG）.Aachen：IEEE，2015：1-8.

[6] 谈发明，王琪.基于改进无迹卡尔曼滤波算法的动力电池SOC估计模型 [J].汽车技术，2019（3）：18-24.

[7] 罗勇，赵小帅，祁朋伟，等.车用动力电池二阶RC建模及参数辨识 [J].储能科学与技术，2019，8（4）：738-744.

[8] GISMERO A，SCHALTZ E，STROE D I. Recursive State of Charge and State of Health Estimation Method for Lithium-Ion Batteries Based on Coulomb Counting and Open Circuit Voltage [J].Energies，2020，13（7）：1-11.

[9] 陈德海，华铭，徐王娟，等.优化安时积分法实时预测电动自行车电池SOC [J].电池，2019，49（1）：41-45.

[10] 王党树，王新霞.基于扩展卡尔曼滤波的锂电池SOC估算 [J].电源技术，2019，43（9）：1458-1460.

[11] AUNG H，LOW K S，GOH S T. State-of-Charge Estimation of Lithium-Ion Battery Using Square Root Spherical Unscented Kalman Filter（Sqrt-UKFST）in Nanosatellite [J].IEEE Transactions on Power Electronics，2015，30（9）：4774-4783.

[12] 宮明辉，乌江，焦朝勇.基于模糊自适应扩展卡尔曼滤波器的锂电池SOC估算方法[J].电工技术学报，2020，35（18）：3972-3978.

[13] ZHANG L Y，ZHANG L，PAPAVASSILIOU C，et al. Intelligent Computing for Extended Kalman Filtering SOC Algorithm of Lithium-Ion Battery [J].Wireless Personal Communications，2018：2063-2076.

[14] 苏振浩，李晓杰，秦晋，等.基于BP人工神经网络模型的动力电池SOC估算方法 [J].储能科学与技术，2019，8（5）：868-873.

[15] 田茂飞，安治国，陈星，等.基于在线参数辨识和AEKF的锂电池SOC估计 [J].储能科学与技术，2019，8（4）：745-750.

[16] CHAO H，YOUN B D，Chung J. A multiscale framework with extended Kalman filter for lithium-ion battery SOC and capacity estimation [J].Applied Energy，2012，92（C）：694-704.

[17] 李嘉波，魏孟，李忠玉，等.基于自适应扩展卡尔曼滤波的锂离子电池荷电状态估计[J].储能科学与技术，2020，9（4）：1147-1152.

作者简介：张帅帅（1995—），男，汉族，安徽蚌埠人，硕士研究生在读，研究方向：锂离子电池状态估计;通讯作者：颜文旭（1971—）男，汉族，福建莆田人，博导，教授，博士，研究方向：电力电子技术及智能控制、电力系统及其自动化。DCD84A21-20B9-4127-8F37-916BA023FC35