Task-adaptation graph network for few-shot learning①

ZHAO Wencang(赵文仓), LI Ming, QIN Wenqian

(College of Automation and Electronic Engineering, Qingdao University of Science and Technology, Qingdao 266061, P.R.China)

Abstract Numerous meta-learning methods focus on the few-shot learning issue, yet most of them assume that various tasks have a shared embedding space, so the generalization ability of the trained model is limited. In order to solve the aforementioned problem, a task-adaptive meta-learning method based on graph neural network (TAGN) is proposed in this paper, where the characterization ability of the original feature extraction network is ameliorated and the classification accuracy is remarkably improved. Firstly, a task-adaptation module based on the self-attention mechanism is employed,where the generalization ability of the model is enhanced on the new task. Secondly, images are classified in non-Euclidean domain, where the disadvantages of poor adaptability of the traditional distance function are overcome. A large number of experiments are conducted and the results show that the proposed methodology has a better performance than traditional task-independent classification methods on two real-word datasets.

Key words:meta-learning,image classification,graph neural network (GNN),few-shot learning

0 Introduction

Plentiful machine learning problems have been solved by the development of deep learning. Based on large datasets and high-dimensional datasets, high prediction accuracy has been achieved in tasks such as computer vision, machine translation, sentiment analysis, as well as speech recognition, and the development of artificial intelligence has also been promoted.However, the following key problem still remains: a large number of labeled samples are required when training models;on the contrary,in the real world,the labeled samples are quite rare or undisclosed, which makes it impossible to train a highly accurate model.The problem mentioned is the few-shot classification problem[1].

In recent years, in order to solve the above fewshot learning problem, researchers have shifted their focus to meta-learning (learning to learn). Thanks to prior knowledge can be used by meta-learning to train a model with strong generalization ability, the most important thing is that it has weak demand for sample labels and has a wide range of applications. The existing meta-learning methods can be divided into the following four categories: meta-learning methods based on parameter optimization, such as MAML algorithm[2];meta-learning methods based on external memory,such as MetaNet algorithm[3]; meta-learning methods based on data enhancement, such as the SGM algorithm[4];meta-learning methods based on metric learning, such as RepMet algorithm[5]. Metric learning is also called similarity learning. Its essence is to complete the fewshot classification by comparing the similarity of two images.

Although stupendous progress has been made by these methods,limitations still remain. First of all,the feature vectors extracted by most methods are not sufficiently distinguishable for new tasks. The main reason is that they do not consider that different classification tasks have different differences between their features,and the feature representation should also be adjusted according to the task. In other words, the feature representation that is applicable to a certain task does not be applicable to other tasks. In order to overcome this shortcoming, a feasible solution is to link the training task with the test task, so that the feature extraction process is more focused on the task to be completed next, rather than extracting feature representations for all classification tasks. Secondly, Euclidean or other artificially defined distance functions are usually used by most of the existing few-shot learning methods based on metric learning, which are limited to a two-dimensional or multi-dimensional space[6]. The solution is to use a neural network to train this metric,so that the distance function can be adjusted according to different tasks.

A self-attention learning module based on the metric learning algorithm is proposed in this paper, which is used to improve the characterization ability of the original algorithm feature extraction network, so that the extracted feature vectors can be applied to various tasks(task-adaptation). In addition, a graph neural network (GNN) is employed as a distance measurement method to overcome the shortcomings of traditional measurement methods and the relationship between samples is fully used to further improve the accuracy of few-shot classification.

1 Related work

The essence of the attention mechanism is to only focus on key information, that is, when multiple types of information appear, only a specific part is captured.A great success in natural language processing, semantic segmentation, image classification and other fields[7]has been achieved.

In recent years, the attention mechanism has been improved and the self-attention mechanism has been produced by researchers, where the ability to capture the internal correlation of features is referred to by attracting attention to each information in a set of information. Similarly, remarkable results in various fields have been achieved by attention mechanism. For example, when completing natural language processing,a self-attention mechanism instead of a recurrent neural network was used to excellently complete the learning of text representation[8]. In Ref.[9], the task of instance segmentation and target detection was completed through adding a non-local module(the modeling method is the self-attention mechanism) to the ResNet network, and the performance was greatly improved. In addition, the task of extracting biomedical relationships was completed through applying the self-attention mechanism in Ref.[10].

Recently, innumerable image classification work have shifted to the attention mechanism[11-13]. Different weights were assigned to different samples in the training set, so that important features were paid more attention by the classification model. In this way, irrelevant information was ignored, however, the sample features in the training set were weighed while the samples in the test set were not considered. That is to say,after the attention mechanism, feature vectors are more conducive to the classification of specific tasks, the generalization ability on other tasks is still not ideal.The reason is that feature vectors should be different for different tasks. For example, two tasks are given, one is to distinguish between lion and tiger, the other is to distinguish between lion and wolf, the difference of lion and tiger must be different from the difference of lion and wolf. If the feature vectors used for classification are the same, the accuracy will be definitely affected. In order to overcome this limitation, a taskadaptive few-shot learning method is proposed.

For the above considerations, the characteristics of the test set samples are merged when the attention weights of the training set samples are calculated, so that the trained model can adapt to various classification tasks. In addition, a large number of existing fewshot classification methods based on metric learning are limited to the use of cosine distance[14],Euclidean distance[15]or nonlinear neural network[16]to calculate similarity, where the correlation between the samples is not sufficiently considered. And the graph neural network model[17]is used as the classification module,that is, the distance measurement is transferred from the Euclidean space to the non-Euclidean space, so as to fully explore the relationship between the samples and further improve the classification accuracy.

2 Problem definition

In this section, the definition of the meta-learning problem and graph classification problem will be introduced.

2.1 Meta-learning problem

Firstly, the specific meaning ofN-wayK-shot will be presented: the unlabeled samples predicted by classification models belong to one of theNcategories, and there are onlyKlabeled samples in each category,whereKis a very small number.N×Ksamples with known labels will be used to make predictions on samples with unknown labels. All the samples mentioned above are from the test set, denoted asDtest, and the set of labeled samples in the test set is also called the support setDsupport, the set of unlabeled samples is called the query setDquery. And the samples inDsupportare denoted asxs, while the samples inDqueryare denoted asxq.

Since there are few samples with known labels,Dtrain, whose samples are all labeled, is used to simulateN-wayK-shot tasks. The specific steps are: randomly selectNclasses from the training set, where there areKsamples in each class, and theseN×Ksamples form support setDsupport, and then randomly selectPsamples from the remaining samples in each category to form query setDquery, and repeat the above stepsMtimes,M N-wayK-shot tasks can be derived.In order to simulate the test task, what need to do is to use the samples in the support set to predict the labels of samples in the query set ,that is,train the model on theMtasks in the training set, and then generalize it to the test set. Usually the classification modelfis trained by minimizing the loss sum of these tasks(Eq.(1)). The specific steps are shown in Algorithm 1.

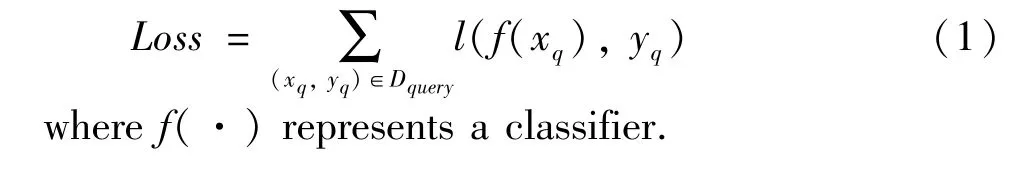
Algorithm 1 The formation process of meta-tasks for all samples x in Dtrain do for each task Ti, ∀i ∈{1,…,M} do Randomly sample N classes from Dtrain;Randomly sample K instances from N classes to form Dsupport;Randomly sample P instances from (Dtrain -Dsupport)to form Dquery;end for end for

2.2 Graph classification problem

The definition of the graph is briefly introduced.Graph is a data structure consisting of two components:nodes and edges. Nodes represent the object of classifying and edges represent the specific relationship between the two objects. An undirected graph can be described as a set of nodes and edges, denoted asG=(V,E),Gis a two-tuple, whereV={v1,v2,…,vi,…,vn} is a node set;E={ei,j=(vi,vj)}⊆(V×V)is an edge set. In addition, the matrix storing the data of the relationship (edge) between nodes is called the adjacency matrix (A)[18].

The graph neural network used for classification in this paper contains two modules: weight update module and node update module. The weight update module is composed of 5 fully connected layers. Four of them have a batch normalization layer and an activation function leaky ReLU layer. In order to learnθ, a fully connected layer is added at the end of the network.When the nodes need to be classified, the softmax function is used to normalize the adjacency matrixArow by row, and outputs the adjacency matrixB,whose elements represent the similarity between nodes.The node update module is composed of graph convolution block and cascading operation layers. Among them,the graph convolution block contains a batch normalization layer and a leaky ReLU layer. The network structure of the graph neural network and its detailed work process is shown in Section 3.

3 Methods

The task-adaptive few-shot learning method will be introduced in this section. Firstly, how the embedding module extracts the initial feature representations is explained. Then the initial feature vectors are operated based on the self-attention mechanism, so that the output of the self-attention module is a series of taskrelated feature vectors. Finally the working process of the classification module (graph neural network) is illustrated.

The visualization of the operation process is shown in Fig.1.

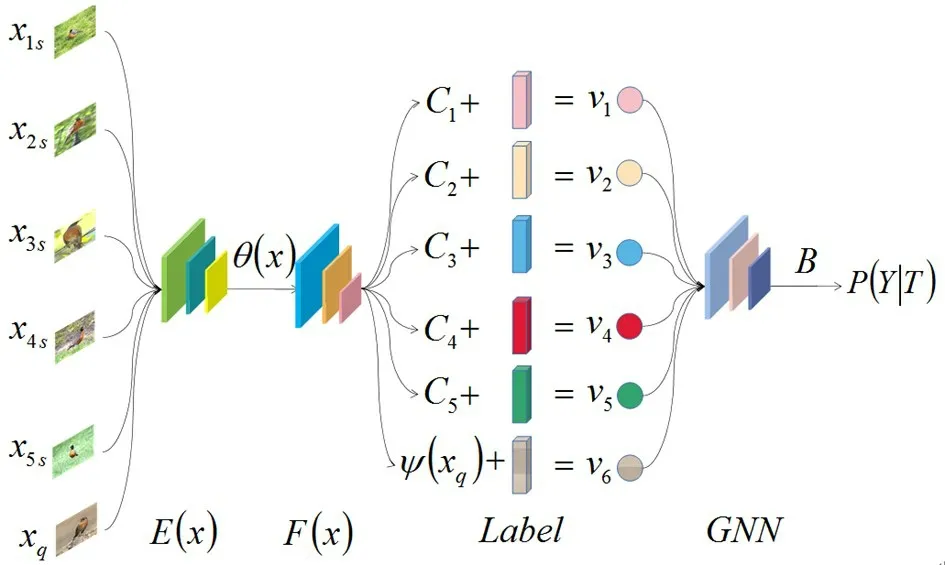
Fig.1 The overview of task-adaptation graph network (TAGN) method

3.1 Feature embedding module

In order to learn the initial feature representationsθ(x)(Eq. (2)) of the inputsx, the prototype network[18]is used as the feature extraction networkE(x)(as visualized in Fig.2). The core of this network is transforming the comparison betweenθ(xq) (the feature vectors of samples inDquery) andθ(xs) (the feature vectors of samples inDsupport) (Eq.(3)) into the comparison betweenθ(xq) andCi(the category center ofDsupport)(Eq. (5)). Among them, the calculation method of the category center ofDsupportis to take the average value of all the sample features in the category(Eq.(4)).

Fig.2 The overview of the network structure of feature embedding module

3.2 Self-attention module

The purpose of self-attention module is to transform the initial feature representationθ(x) unrelated to the task into a task - adaptive feature representationψ(x) (Eq.(7)). The specific operation steps are based on the self-attention mechanism, that is, a converterFis introduced, whose function is to calculate the correct value corresponding to the query point. It is a store of triplets, which is composed of query, key and value[8]. Among them,the query vector represents the feature of the sample, the key vector represents the feature of the information, and the value vector represents the content of the information. The way of defining them will be described later.

To convert the task-independent feature vectorsθ(xq) to the task-adaptive feature vectorsψ(xq), the‘self-attention’ operation is utilized, and the scaling dot is used to get the self-attention score. In addition,the self-attention module consists of a fully connected layer, a matrix multiplication layer, and a softmax normalization layer. In order to improve the generalization ability of the model and prevent overfitting, a dropout layer (which rate is set as 0.5) is added to the network structure. In addition, in order to make the final model more stable and effective, layer normalization layer instead of batch normalization layer is utilized at the end, and its network structure is shown in Fig.3.

3.3 Classification module

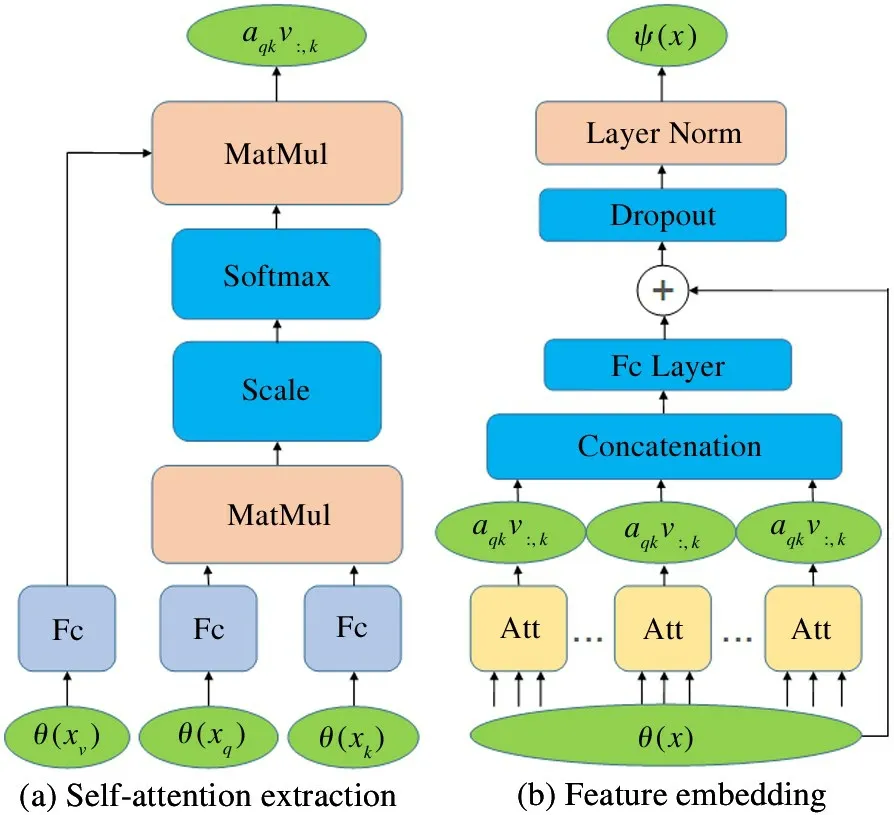
Fig.3 The overview of the network structure of self-attention module

As mentioned in subsection 3. 1, the center of task-adaption feature representationψ(x) will be obtained firstly according to Eq.(12),and then the category centerCiand query set sample representations will be connected with their labels. For test samples that do not know the labels,h(l) is defined as a uniform distribution function(for the sake of simplicity, the label is filled with all 0) (Eq.(13)), and the spliced feature vectors are regarded as nodes, denoted asV={v1,v2,…,vi,…,vn}, wheren=N+P(Pis the number of sample points inDquery), which will be the inputs of the graph neural network.

whereGc(·) represents a neural network layer,ρ(·) represents the activation function leaky ReLU,dis the number of rows of the node vector, andBis the adjacency matrix normalized by softmax for each row of the adjacency matrixA.

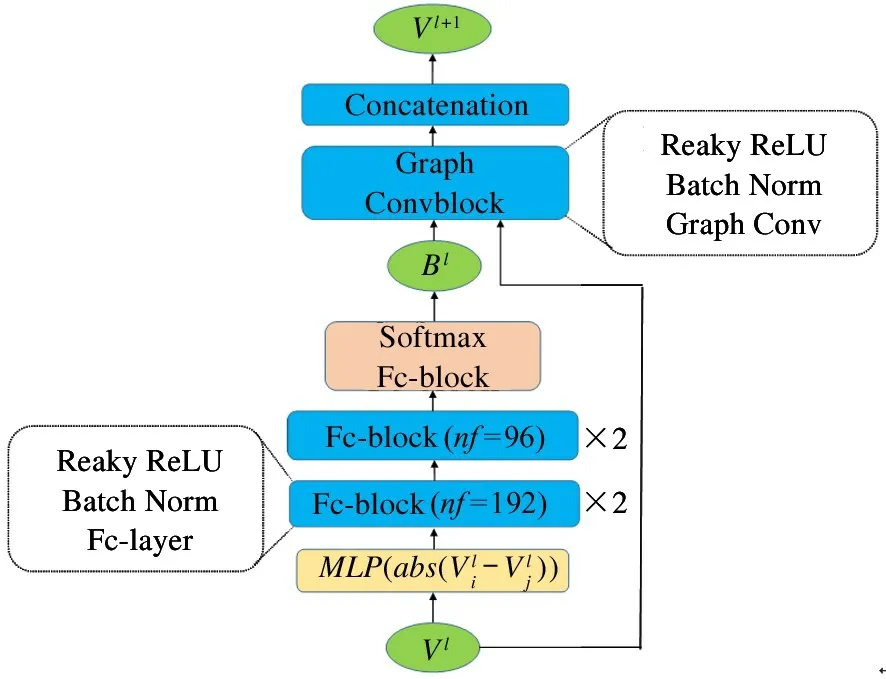
Fig.4 The overview of the network structure of classification module

Algorithm 2 Training strategy of task-adaption graph network Inputs: DSupport = {(x1, y1),…, (xN×K, yN×K)}; Dquery ={x1,…,xP}Outputs: labels y of samples in Dquery for all M tasks do Calculate θ(x) using Eq.(2);Calculate aqk using Eq.(10);Calculate ψ(x) using Eq.(11);Calculate Ci using Eq.(12);Connect Ci, ψ(xj) with its labels using Eq.(14)→V= (v1,…, vN+P);for all layers=1,…, l do Calculate Al using Eq.(14);Calculate Vl+1 using Eq.(15);Predict the labels ypq of xq using adjacency matrix B;Calculate the loss function l(ypq,yq)using Eq.(16);end for Calculate the gradient of Loss using Eq.(1);Update E, F and GNN with the gradient of Loss using stochastic gradient descent;end for

wherekis the number of samples inDquery.

4 Experiments

The performance of the task-adaptation method on two general datasets (MiniImageNet and CUB200-2011) is shown in this section. Firstly, a brief introduction to the two datasets and their category allocation is given. Then the accuracy of the proposed method and baselines is compared to verify the advancement of the proposed method based on two backbone networks.Finally ablation experiments are conducted to further test the significance of each module in TAGN.

4.1 Datasets

MinilmageNet(Mini) dataset[15]is excerpted from the ImageNet dataset and it is the benchmark dataset in the field of meta-learning and few-shot learning. It contains 100 categories of 60 000 images. And there are 600 samples in each category.

CUB200-2011(CUB) dataset[15]is a fine-grained dataset presented in 2010, and it contains 200 categories of 11 788 images. More about the setting methods of these two datasets are shown in Table 1.

Table 1 Descriptive statistics of datasets

4.2 Backbone networks

Two traditional feature extraction networks are used asE(x), namely four-layer convolution network(ConvNet-4) and residual network (ResNet-12).Next, they will be introduced in detail.

ConvNet-4 consists of 4 identical convolutional blocks, and each convolutional block contains a 3 ×3 convolutional layer, a batch normalization layer, an activation function layer and the maximum pooling layer for compression. And in order to reduce the amount of calculation for subsequent operations, a global max pooling layer (GMPL) that reduces the dimension of feature representation is added at the end. Its network structure is shown in Fig.2(a).

ResNet-12 is composed of 4 convolutional blocks,and each convolutional block contains a 3 ×3 convolutional layer, a batch normalization layer, and an activation function layer. Also in order to reduce the amount of calculation, a global average pooling layer (GAPL)is added at the end. Its network structure is shown in Fig.2(b).

4.3 Results and discussion

Table 2 and Table 3 indicate the results of the performance comparison between task-adaptive method and baselines, where the model of this paper achieves the best performance on two datasets. Among all models, two non-linear neural networks-based models, relation network and GNN, have shown better results,compared with traditional distance function-based models matching network and prototypical network. For example, in 5-way 1-shot setting the accuracy of GNN improved by at least 0.16% (50.46% vs. 50.62%)on MiniImageNet and 1.27% (62.45% vs. 63.72%)on CUB200-2011,while in 5-way 5-shot setting the accuracy of GNN improved by 0.62% (65.85% vs. 66.47%)on MiniImageNet and 5.44% (76.12% vs. 81.56%)on CUB200-2011. To further demonstrate the advancement of the method of this paper, it is compared with EGNN[20]and TPN[21], where the accuracy is improved by at least 0. 97% (52. 46% vs. 53. 43%)and 1.05% (81.64% vs. 82.69%), under 5-way 1-shot setting and 5-way 5-shot setting compared with EGNN,and the accuracy is improved by at least 0.08%(53. 35% vs. 53. 43%) and 0. 97% (81. 72% vs.82.69%),under 5-way 1-shot setting and 5-way 5-shot setting compared with TPN (as shown in Table 2 and Table 3).

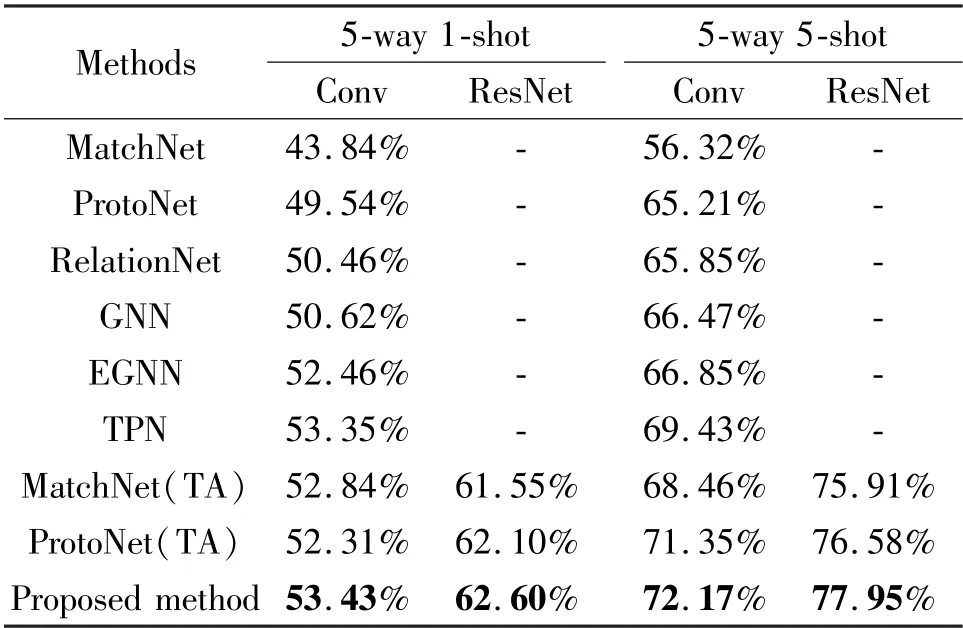
Table 2 Few-shot classification accuracy on MiniImageNet dataset

In addition, in order to verify the effectiveness of the task-adaptation module (TA), a self-attention module is added to the original structure of the matching network and the prototype network. The results show that due to the addition of the self-attention mechanism on MiniImageNet, the accuracy of matching network has increased from 43.84% to 52.84% (5-way 1-shot setting), the accuracy of prototype network increased from 49.54% to 52.31% (5-way 1-shot setting).

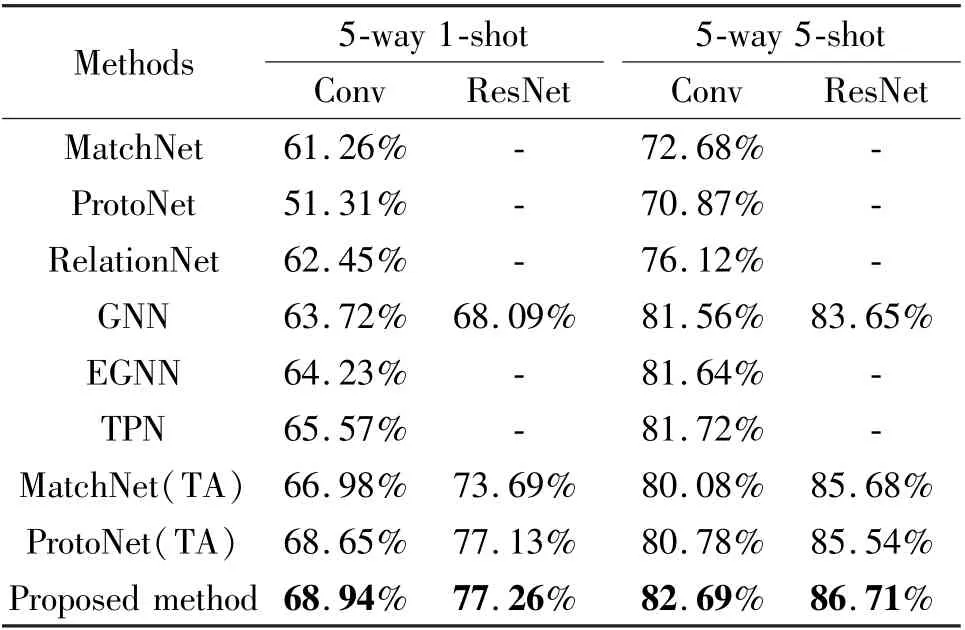
Table 3 Few-shot classification accuracy on CUB200-2011 dataset

As for CUB200-2011, the accuracy of the matching network increased from 62.26% to 66.98% (5-way 1-shot setting), the accuracy of prototype network has risen from 51.31% to 68.65% (5-way 1-shot setting). This proves that the motivation using self-attention module as supplement to feature extraction module gets benign results. Moreover, the task-adaptive graph neural network has at least improved accuracy compared with the task-unknown baselines 0.5% (62.10% vs.62.60%) and 0. 13% (77. 13% vs. 77. 26%) for MiniImageNet and CUB200-2011 respectively. It implies that the model that uses self-attention mechanism to get task-adaptation feature vector and then utilizes GNN as classification module has received well performance.

4.4 Ablation experiments

To predict how the regularizationλimpacts the results, another experiment is implemented, where the value ofλis changed and all other parameters are fixed to the values that produce the best results. In addition,the value ofλis set as 0,1,10, 100, and the changes of classification accuracy are observed based on ConvNet-4 on the dataset MiniImageNet. The results show that when the value ofλchanges within a certain range, the accuracy is increased. And models perform well when the value ofλ=10. The overall operational results is depicted in Fig.5.

In order to prove the advancement of TAGN,comparative experiments are conducted on the MiniImageNet dataset and CUB200-2011 dataset based on ConvNet-4. Among them, the comparison baselines are the matching network using the cosine distance, the prototype network using the squared Euclidean distance,and GNN which changes the distance measurement from the Euclidean domain to the non-Euclidean domain. Results are shown in Fig.6, where MatchNet,ProtoNet, GNN and TA represents matching network,prototype network, graph neural network and the selfattention (task-adaptation) module, respectively. The results prove that the methods of training the metric function with neural network are better than the traditional methods of fixed distance function.

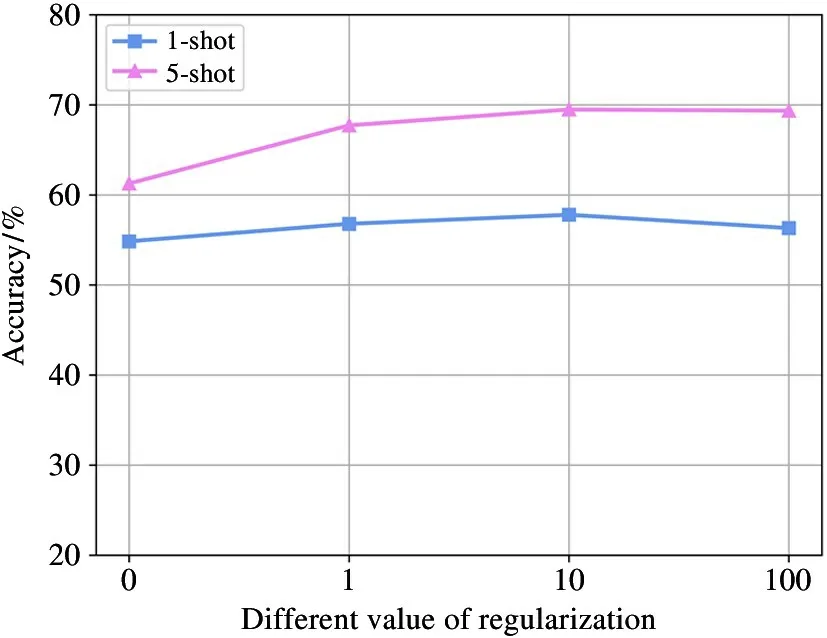
Fig.5 Line chart of the accuracy for different value of regularization

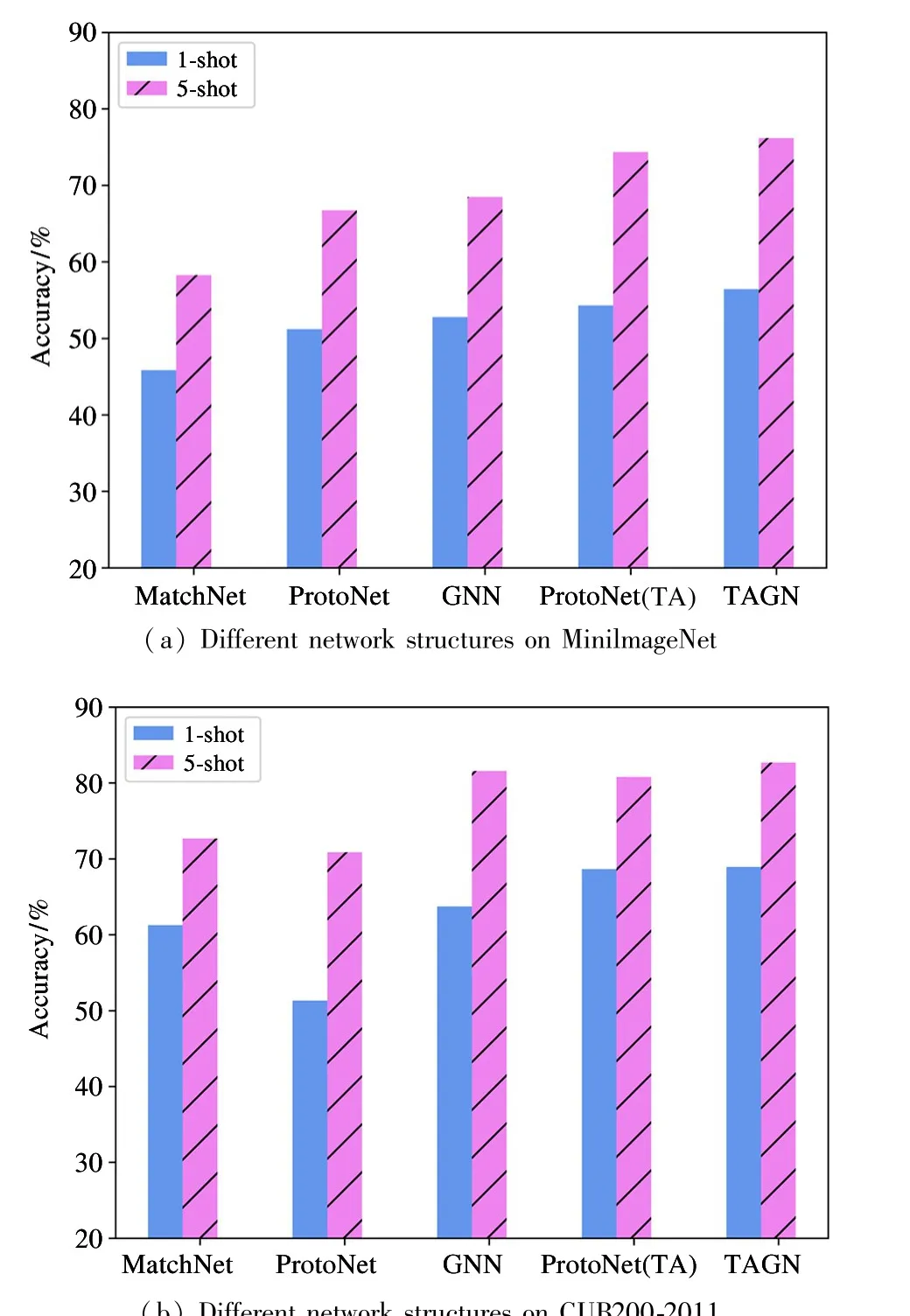
Fig.6 Histogram of the accuracy for different network structure

As for the accuracy on the MiniImageNet dataset,the addition of self-attention module improves the accuracy from 49.54% and 65.21% to 52.31% and 71.35%,under 1-shot and 5-shot settings, respectively. And the method TAGN increases the accuracy by at least 2.21% (52.31% vs. 54.43%) and 0.82% (71.35%vs. 72.17%) under 1-shot and 5-shot settings. As for the accuracy on the CUB200-2011 dataset, the addition of self-attention module improves the accuracy from 51.31% and 68.65% to 70.87% and 80.78%, under 1-shot and 5-shot settings,respectively. And the method TAGN increases the accuracy by at least 0.29% (68.65%vs. 68.94%) and 1.13% (81.56% vs. 82.69%)under 1-shot and 5-shot settings.

5 Conclusions

A feature learning model based on the metric learning algorithm is proposed in this paper, where the self-attention mechanism is utilized to produce taskadaption feature vectors and adaptable model. In addition, a classification framework based on graph neural network is established, where the relationship between samples can be fully explored by the model, and the effect of improving the accuracy of few-shot classification can be achieved. The experimental results on the datasets MiniImageNet and CUB200-2011 prove that the method of this paper is better than task-independent methods. In the future, the model will be extended to the two settings including zero-shot classification and generalized few-shot classification.