基于改进剪切应力输运k-ω湍流模型对考虑风向随高度偏转大气边界层的数值模拟
2022-07-06冯成栋
冯成栋,顾 明
(同济大学土木工程防灾国家重点实验室,上海 200092)
当前,计算风工程(computational wind engineering,CWE)在结构风工程领域的研究与应用越来越广泛。在计算风工程中,正确模拟不可压缩中性层结水平均匀稳态正压的大气边界层(以下简称“大气边界层”)是非常重要的一项工作,它直接关系到后续建筑绕流模拟的准确性。所谓“水平均匀”,是指各流动物理量的水平梯度为零,大气边界层风特性在入口到模型之间不发生明显的变化,也即大气边界层的“自保持”。为了满足这一要求,诸多学者从不同方面进行了研究。Richards 和Hoxey[1]基于标准k-ε模型,提出了一组适用于近地层的边界条件。这组边界条件已得到广泛应用[2-3]。Blocken等[4]、Hargreaves和Wright[5]、方平治等[6]据此对壁面函数以及粗糙度参数进行修正,以实现近地面风场的准确模拟和自保持。Yang等[7-8]推导了近似满足大气边界层自保持要求的湍动能表达式,建议了一组新的入流边界条件,将其成功应用于标准k-ε模型和剪切应力输运(shearstress transport,SST)k-ω模型。唐煜等[9]基于SSTk-ω模型和平衡湍流假设,推导了适用于一般风工程计算的入口来流边界条件表达式,并给出了适用于地形尺度风场计算的湍流模型常数建议值。Parente等[10-11]、Longo 等[12]则对k-ε两方程分别添加了源项,以实现入流边界条件和湍流模型方程的相容。Hargreaves 和Wright[5]、O’Sullivan 等[13]、Richards 和Norris[14]特别强调了流域顶部边界条件对于实现自保持的重要性。
然而,以上研究仅着眼于近地层特性的模拟。实际上,大气边界层由近地层和Ekman层组成,其中的气流可近似看作是水平气压梯度力、科里奥利力和湍流摩擦力平衡的结果。“三力平衡”不仅导致了平均风速随高度的增加而增加,也导致了平均风向随高度的增加而沿顺时针方向偏转(北半球)。图1给出了大气边界层中风向随高度的变化示意图(θ表示风偏角,Vgr表示梯度风高度处的风速),称为“Ekman 螺线”[15]。一般认为,近地层高度数值在20~200 m 左右[16],此范围内风向基本不随高度变化,而在约占大气边界层总高度90%的Ekman 层中,风向随高度的偏转表现得尤为显著[17-18]。
近年来,全球出现了多座超过500 m 高度的超高层建筑,如上海中心大厦(Shanghai Tower,632 m,2015)、哈利法塔(Burj Khalifa Tower,828 m,2010)等,而在规划中的国王塔(Kingdom Tower)更是超过1 000 m。对这些千米级超高层建筑而言,高空风特性将会对风荷载和风致响应产生很大影响,甚至可能是决定性的。我国现行建筑结构荷载规范[19]认为各类地貌梯度风高度以上平均风速大小保持不变,但是近来有研究表明,在千米量级附近,平均风速随高度单调增加[20]。另外,荷载规范也没有考虑风向随高度偏转。风向随高度的偏转将使得千米级建筑的风力沿高度分布和响应更加复杂[21],在结构设计时应该引起高度重视。从基本方程出发,对考虑风向随高度偏转的大气边界层进行计算流体动力学(computational fluid dynamics,CFD)数值模拟和自保持实现方法的探讨,是研究千米级建筑风荷载和风致响应特性的基础。
SSTk-ω模型能够有效计算湍流切应力在逆压梯度边界层的输运,被视为目前RANS(Reynoldsaveraged Navier-Stokes)方法中最适用于钝体分离流模拟的两方程湍流模型[22]。为了与后续建筑绕流模拟工作衔接,本文基于SSTk-ω模型,通过修改模型参数、方程源项和湍动粘度,提出了“改进SSTk-ω模型”,并采用该模型对考虑风向随高度偏转的大气边界层进行了CFD数值模拟。通过预前模拟和主模拟两个步骤,对风场自保持的实现方法进行了探讨。通过对比CFD模拟结果和实测结果,验证了改进SSTk-ω模型模拟结果的合理性;通过出流面和入流面各物理量的对比,验证了自保持方法的有效性。
1 预前模拟
所谓预前模拟,是指在模拟主要研究对象之前,设立单独的计算域,对入口湍流进行模拟,而后将模拟得到的入口湍流施加于主模拟计算域的方法。由于本文研究的大气边界层满足稳态假定和水平均匀性假定,因此并不涉及时间存储的问题,且预前模拟只需满足竖向的网格划分与随后主模拟所用网格的竖向划分一致即可,在水平方向可以采用数目较少的网格。这种方法可在模拟精度达到一定要求的前提下,节省计算资源,因此在气象学的相关模拟、地形风场模拟和建筑绕流的前期风场模拟中被广泛采用[2,13,23]。
基于SSTk-ω模型,通过修改模型参数、方程源项和湍动粘度,对考虑风向随高度偏转的大气边界层进行预前模拟,为后续主模拟提供入口信息。
1.1 基本方程
引入不可压缩中性层结水平均匀稳态正压大气边界层假定,忽略分子粘度,并假定垂直方向运动与水平方向运动相比可以忽略,则连续性方程自动满足,水平方向的动量方程可以简化为
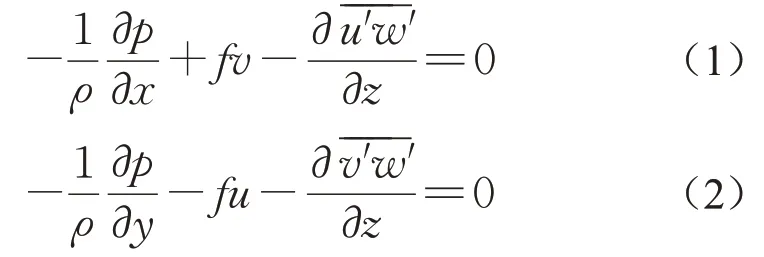
式中:(u,v)为水平平均风速分量;p为压力;ρ为空气密度;f为科里奥利参数(f=2ωsinφ,φ为纬度,ω为地球自转角速度);′和′表示雷诺应力(湍流切应力)。式(1)和式(2)等号左端从左到右依次为水平气压梯度力、科里奥利力和湍流摩擦力。上述方程称为经典Ekman 模型(也称为“三力平衡”模型)。
为了使动量方程闭合,引入Boussinesq 假定,将雷诺应力与平均速度梯度联系起来:

式中:μt为湍动粘度;k为湍动能。
冯成栋和顾明[24]已通过修改标准k-ε模型的基本参数,对考虑风向偏转的大气边界层进行了模拟。为了与后续建筑绕流模拟工作衔接,本文将大气边界层模拟方法推广至SSTk-ω模型,即从k-ε模型方程出发,根据相关数学关系,推导得到适用于SSTkω模型的、可实现大气边界层内风向偏转的改进方案。推导过程如下。
引入比耗散率ω=ε/(Cμk)(其中ε为湍动能耗散率,Cμ为模型常数),将其代入简化的标准k-ε模型方程中(参照文献[24]中公式(4)—(6)),可得(忽略源项Sk和Sε):

式中:Gk为湍动能生成项;C1ε、C2ε、σk和σε均为模型常数。
化简式(6),并用式(6)-式(5)乘以ω可得:

式(7)两端同除以k,可得:

结合比耗散率定义和式(4),进一步简化式(8)得:

若令σk=σε=σω,则式(9)可进一步简化如下:
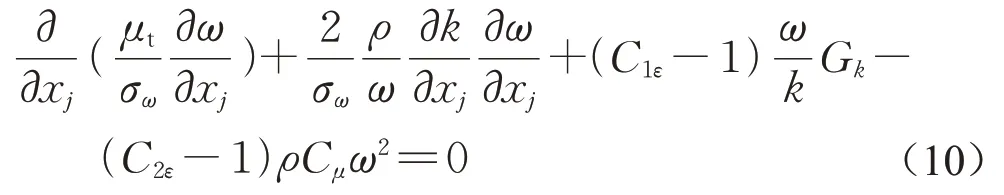
令C1ε-1=C1ω,C2ε-1=C2ω,为了 将Apsley 和Castro[25]提出的方法推广至SSTk-ω模型,参照文献[24]中的公式(7),将式(10)等号左端的C1ω(=C1ε-1)用C*1ω替代,如式(11):
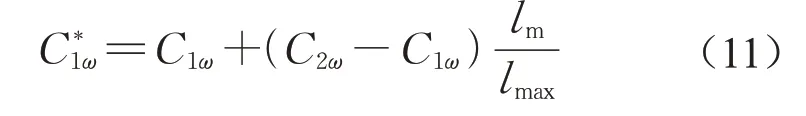
式中:lmax表示边界层最大混合长度;lm为局地混合长度(即湍流长度尺度),用式(12)计算:

综上,为了使大气边界层模拟结果更加接近实测,基于SSTk-ω模型的改进方案如下(简化起见,取σk=σε=σω):

式(13)—(15)表达的模型在本文中被称为“改进SSTk-ω模型”。需要注意的是,该模型方程与ANSYS Fluent 15.0 内置的SSTk-ω模型方程有所区别,为此,应当参照ANSYS Fluent Theory Guide[26]中SSTk-ω湍流模型方程,通过UDF(userdefined function)中的源项宏和湍动粘度宏,对内置的SSTk-ω模型方程进行修改,使之与式(13)—(15)吻合。
1.2 模型参数
湍流模型常数的取值,随研究问题性质的不同而异。诸多研究表明,Cμ在大气边界层的模拟中,取值当与默认推荐值不同,常取Cμ≈0.03[7,23]。需要注意的是,Cμ在SSTk-ω模型中对应β*∞,故其值也应取为0.03。C1ε和C2ε的取值参考文献[23],分别取为1.52 和1.833,故C1ω和C2ω应 分 别 取 为0.52 和0.833。关于σε,应由以下约束关系确定,以使在近地层中能够再现对数律[23]:

式中:κ为冯·卡门常数κ,可取0.42。σk和σω的取值则没有严格规定,简化起见,可取σk=σω=σε。另外,对比式(15)与ANSYS Fluent Theory Guide[26]中SSTk-ω模型方程可以发现,C2ω×Cμ对应SSTk-ω模型常数βi。
除了本身的模型常数外,式(11)还引入了参数lmax。Koblitz 等[23]指出,lmax取28 m(实尺)时,模拟结果和实测结果[27]吻合得很完美。本文采用此值。
表1 给出了ANSYS Fluent 15.0 内置SSTk-ω模型常数的推荐取值和本文大气边界层模拟所用改进SSTk-ω模型常数取值(仅列出有改动的模型常数)。

表1 模型常数取值Tab.1 Model constant values
1.3 目标风场和相似准则
常规大气边界层风洞的风场模拟中,往往只关注平均风剖面、湍流度剖面、脉动风速功率谱和湍流积分尺度等。然而,在真实的大气环境中,风场是水平气压梯度力、科里奥利力、湍流摩擦力等相互作用的结果,Ekman 层内的风速矢量呈现出随高度偏转的普遍特征[28-29]。本文拟采用著名的Leipzig实测风剖面作为大气边界层数值模拟的目标风场。Leipzig风剖面于1931 年由探空测风气球测得,并经Lettau于1950 年重新复核[27]。表2 给出了Leipzig 实测风剖面的风场参数,G为地转风速,φ为纬度,u*为摩擦速度,z0为空气动力学粗糙长度,f为科里奥利参数,θ0表示地面附近水平风速矢量到水平地转风速矢量的总风偏角。关于目标风场的湍动能剖面,有大量现场实测和数值模拟资料可供参考[30-32]。
建筑结构的风洞试验和数值模拟通常采用缩尺模型。为了与后续建筑绕流模拟工作衔接,可根据常规风洞试验的风场参数和相似准则,确定各物理量的缩尺比。本文在数值模拟中,采用的几何缩尺比λL为1:1333、风速缩尺比λV为1:1.12,密度缩尺比λρ为1:1,在此缩尺比下得到的Leipzig 风剖面参数u*和z0与TJ-2 某风洞试验[33]目标风剖面取值相同。此外,由于动量方程式(1)和式(2)引入了科氏力,故必须考虑动力气象学中罗斯贝数Ro 相似,罗斯贝数Ro定义如下:

式中:V表示特征速度;L表示特征长度;f为科里奥利参数。由罗斯贝数相似准则可以导出科里奥利参数f的缩尺比:

缩尺后用于数值模拟的Leipzig 风剖面的风场参数一并示于表2。

表2 Leipzig风剖面参数Tab.2 Leipzig wind profile parameters
1.4 网格划分
为了验证本文大气边界层预前模拟结果的网格无关性,采用表3中的三组网格方案,水平向网格均匀划分,高度方向网格采用增长比率,由密到疏。

表3 预前模拟所用网格Tab.3 Grids for precursor simulations
1.5 边界条件和求解设置
大气边界层预前模拟采用的边界条件设置见图2和表4。

表4 预前模拟边界条件Tab.4 Boundary conditions for precursor simulations

图2 预前模拟边界条件Fig.2 Boundary conditions for precursor simulations
假定地转风方向平行于x轴,为了驱动空气形成风场,需要施加压力梯度。考虑到在正压大气边界层中,水平气压梯度力不随高度变化,则其值可由地转平衡关系推导得到:

式中:ρ为空气密度;f为科里奥利参数;(ug,vg)为地转风速分量。
为了使风向随高度形成偏转,需要在动量方程中以源项形式加入科氏力,可通过UDF(user-defined function)源项宏实现。为了使模拟结果更加接近实测,“改进SSTk-ω模型”需借助UDF源项宏和湍动粘度宏实现。
本文数值模拟采用ANSYS Fluent 15.0模拟平台,稳态求解,设置压力速度耦合方式为SIMPLEC,动量方程和湍流模型方程非线性对流项采用二阶迎风格式离散,压力插值格式采用Standard,梯度插值方法采用Least Squares Cell Based。所有变量和连续性方程的残差收敛标准设置为10-6。
1.6 模拟结果分析
图3~图7 分别给出了预前模拟所得平均风速u、平均风速v、平均合风速Uavg、平均风偏角θ随高度的变化曲线,以及量纲一化湍动能随量纲一化高度(大气边界层高度h取Detering 和Etling[34]给出的1600 m,缩尺后为1.2 m)的变化曲线,并将Leipzig实测结果[27]、Ekman 理论解[28]、同济大学TJ-2 某风洞试验目标风剖面[33]及其对数律拟合曲线、ESDU(engineering sciences data unit,英国工程科学数据库)规范平均风剖面[35],以及由Detering 和Etling[34]推演得到Leipzig 实测中的湍动能、Brost 等[30]和Grant[31]的湍动能实测结果、Esau[32]针对不同大气边界层高度h的LES模拟得到的湍动能结果一并示于图中,以资比较。
由图3~图7可见,无论是平均风速、风偏角,还是湍动能,模拟结果均与实测结果吻合得很好。由于经典Ekman 解的前提是湍动粘性系数为常量(缩尺后此处取为0.0053 m2·s-1),所以其值与模拟结果有一定的偏差,但是趋势一致。对于量纲一化湍动能,本文模拟结果与实测结果较为吻合,且基本落在LES 模拟结果范围内。总体来讲,本文大气边界层模拟结果合理,可以满足后续自保持研究和建筑绕流模拟的需要。

图3 平均风速u随高度的变化Fig.3 Profiles of mean velocity component u with height

图7 量纲一化湍动能随量纲一化高度的变化Fig.7 Profiles of non-dimensional turbulent kinetic energy with non-dimensional height
值得注意的是,对数律平均风剖面对真实大气边界层风速存在严重低估。具体说来,图5 中的“TJ-2 目标风剖面对数律拟合”得到的u*和z0与表2缩尺之后的Leipzig 风剖面对应参数(“模拟”栏)相同,但由图5可见,对数律平均风剖面仅在近地层范围内有效,其适用高度为100 m左右,这与Li等[36]和Drew 等[37]通过分析实测结果得到的对数律在高空风的预测中对实际风速低估的结论相吻合。此外,ESDU规范平均风剖面[35]与实测平均合风速结果总体上较为接近(在较高位置处存在低估,但相比对数律风剖面已有明显改善),然而尚不能准确反映风向沿高度偏转的规律。
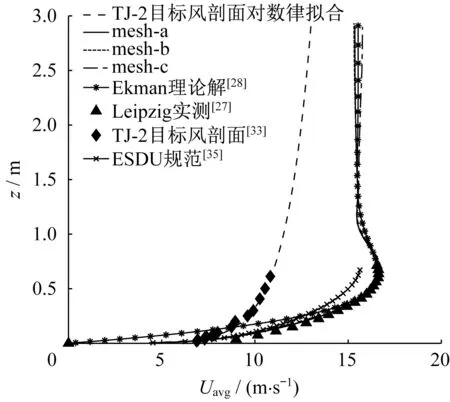
图5 平均合风速随高度的变化Fig.5 Profiles of mean velocity magnitude with height
2 主模拟
大气边界层风场自保持的实现至少需要处理以下三方面的相容问题:①来流边界条件和湍流模型的相容问题;②壁面函数和湍流模型的相容问题;③来流边界条件和壁面函数的相容问题[6]。预前模拟得到的大气边界层风场可以很好地与壁面函数和湍流模型相适应[13],而壁面函数和湍流模型的相容问题已由CFD计算软件(如ANSYS Fluent 15.0)内置解决。因此,采用预前模拟和主模拟两个步骤可使以上三方面问题基本解决,从而较好地实现大气边界层风场的自保持。
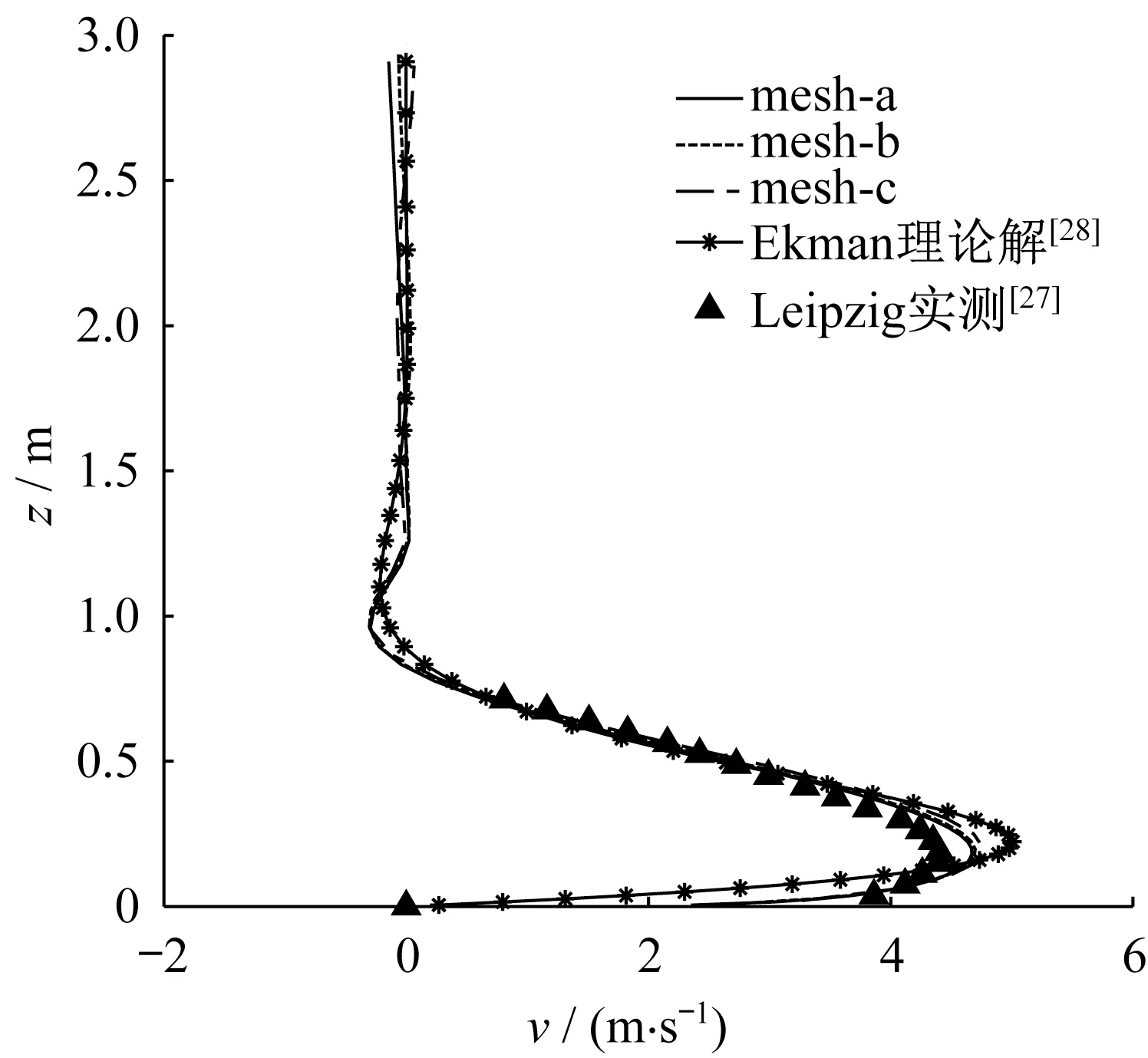
图4 平均风速v随高度的变化Fig.4 Profiles of mean velocity component v with height

图6 平均风偏角随高度的变化Fig.6 Profiles of mean wind veering angle with height
2.1 网格划分
为了验证本文大气边界层主模拟结果的网格无关性,采用表5中的三组网格方案,水平向网格均匀划分,高度方向网格采用增长比率,由密到疏。

表5 主模拟所用网格Tab.5 Grids for main simulations
2.2 边界条件和求解设置
在主模拟中,采用UDF 将1.6 小节中改进SSTk-ω模型预前模拟所得平均风速剖面、湍动能剖面和比耗散率剖面以入流边界条件的形式施加于主模拟区域入口。需要特别说明的是,由1.6小节图3~图5 可见,在相当一部分高度范围内,平均风速大小超越了地转风速G(表2),且在平均风向与地转风向第一次平行后,平均风速的v分量出现了负值,这一现象已为诸多实测和理论分析所证实[16]。这种“超地转”现象导致了主模拟区域边界条件指定的复杂性,特别是给侧向边界的指定增加了难度;侧向边界的回流对应于平均风速v分量的负值,这意味着侧向边界的入流和出流情况很难明确地予以指定[38]。为了克服这一困难,可以将1.6 小节模拟所得来流风场整体旋转一定的角度,而流域外轮廓保持不变。方便起见,可将来流风场整体顺时针旋转26.1o(此角度为来流地面风与地转风的夹角,参见表2),即将“原地面风”和“原地转风”旋转至“新地面风”和“新地转风”的位置,如图8 所示。在新的来流风场下,流域边界的鉴定比较明确,在出流边界不会出现回流现象,因而更加合理。图9和表6给出了大气边界层主模拟边界条件设置。

表6 主模拟边界条件.Tab.6 Boundary conditions for main simulations
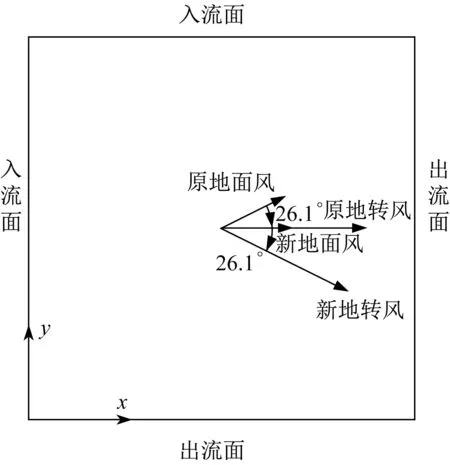
图8 来流风场旋转示意图Fig.8 Overall inflow rotation diagram
此外,由于以速度入口边界给定的风场风向已随高度偏转,且速度入口边界可作为“风场驱动源”[38],故可在主模拟中去掉动量方程中的科氏力源项和水平压力梯度驱动项。为了实现风场自保持,预前模拟中改进SSTk-ω模型添加的源项宏和湍动粘度宏仍需在主模拟中添加。其余参数设置和求解设置同前。
2.3 模拟结果分析
图10~图12分别给出了入流面(inlet)和出流面(outlet)的平均合风速Uavg、平均风偏角θ和湍动能k随高度的变化曲线。由图可见,虽然在地面附近出流面的各物理量相比入流面有所变化,但是总体而 言,大气边界层风场在流域中得到了较好的保持。

图10 出流面与入流面的平均合风速对比Fig.10 Comparison of mean velocity magnitude of inlet and outlet

图12 出流面与入流面的湍动能对比Fig.12 Comparison of turbulent kinetic energy of inlet and outlet
3 结论
本文基于SSTk-ω模型,通过修改模型参数、方程源项和湍动粘度,提出了“改进SSTk-ω模型”,并采用该模型对考虑风向随高度偏转的大气边界层进行了CFD 数值模拟。通过预前模拟和主模拟两个步骤,对风场自保持的实现方法进行了探讨。得到如下结论:
(1)本文提出的“改进SSTk-ω模型”引入了比耗散率生成项和湍流长度尺度之间的反馈机制,综合考虑了模型参数取值的合理性,可取得与大气边界层实测较一致的模拟结果。对数律平均风剖面仅适用于近地层,对高空风速存在严重低估的现象。ESDU规范风剖面对整个大气边界层平均风速预测较好,但尚不能准确反映风向沿高度偏转的规律。

图11 出流面与入流面的平均风偏角对比Fig.11 Comparison of mean wind veering angle of inlet and outlet
(2)通过预前模拟和主模拟两个步骤,即把“改进SSTk-ω模型”预前模拟得到的风剖面以入流边界条件的形式施加于主模拟入口,平均风速、平均风偏角和湍动能均可以在流域中得到较好的保持。
(3)本文提出的“改进SSTk-ω模型”,是对已有修正k-ε模型的推广,丰富和完善了考虑风向偏转的大气边界层RANS模拟方法。基于此进行的大气边界层风场模拟及自保持方法研究,可为后续建筑绕流模拟提供前提和基础。由于SSTk-ω模型在钝体分离流模拟中更具优势,因而“改进SSTk-ω模型”可在实现偏转风场准确模拟的基础上,对建筑平均风压和绕流进行较为精准的预测。
