船体兴波阻力快速预报方法研究

陈帅，王超，周广利，蒋彩霞

1. 中国船舶科学研究中心，江苏 无锡 214082

2. 哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001

船体兴波阻力快速预报是船型优化设计方法研究的关键技术之一，它可以通过求解定常兴波问题得到。现在主流的船舶兴波阻力预报的理论方法有基于势流理论的Rankine源面元法（Dawson法）、Neumann-Michell （NM）理论[1-4]和考虑黏性的计算流体动力学(computational fluid dynamics,CFD)技术。CFD方法由于求解Navier-Stokes方程需要数小时或更长时间，其适用于评估设计，很难满足船型优化高效的要求。在上两个世纪中，出现了一些经典的兴波势流理论，如Michell理论、Kelvin源（或Havelock源）、Neumann-Kelvin（NK）理论和新细长体理论等，这些理论为后续的兴波问题研究奠定了基础。

Dawson[5]在自由面和船体表面布置Rankine源1/r来求解定常兴波问题，使得Dawson法在船舶兴波阻力预报上取得了巨大的成功。Tarafder等[6]提出了一种改进的Dawson方法计算了Wigley和S60船型的阻力和波高分布，自由面采用贴体网格代替流线网格，其预报值与实验值误差较小。Rabaud等[7]基于Dawson法考虑了非线性的影响，预报了Wigley和KCS船型的阻力、纵倾、升沉和自由面波高，其预报值与实验值误差较小。

在国内，张宝吉等[8-10]利用Dawson法对船体兴波阻力进行数值预报，并应用于某高速水面舰船进行优化设计。程京普等[11]提出了一种改进的Dawson方法，采用静水面贴体网格代替流线网格，对方尾船型的兴波阻力进行预报并验证。范井峰等[12]利用Dawson方法预报了小水线面双体船在不同航速下的兴波阻力、升沉和纵倾等，并与实验结果进行了对比。何广华等[13]建立了一种水下航行体兴波尾迹和兴波阻力的快速分析模型，其Rankine源项采用Newman解析法进行求解。

国内外更多针对Dawson方法的应用以及考虑非线性因素等，缺乏对求解过程的计算效率分析和研究，鉴于此，本文编写了基于贴体网格的Dawson方法计算程序，引入加速大规模并行计算(accelerated massive Parallelism, AMP)技术，建立了船体兴波阻力快速预报模型。本文开发的程序只需数十秒就可以计算一次兴波，适用于船舶初步设计和船型优化。

1 理论与数值离散模型

1.1 兴波理论

本文采用C++语言自编程开发，基于Dawson法的兴波阻力计算步骤[2]：1) 在船体表面上用面元法计算叠模扰动流；2) 在船体表面和自由面上利用物面边界条件、自由边界条件和辐射条件计算兴波扰动流，把求解的叠模绕流和兴波扰动流问题转化为求解船体表面和自由面分布源点强度问题：

式中：U为航速；Φ为总速度势，满足拉普拉斯方程；φr为叠模扰动速度势；φw为兴波扰动速度势；为叠模表面源强；σB和σF分别为船体表面和自由面源强；SB为船体表面；SF为自由面；rpqb、rpqw为场点p到船体表面上点qb和自由面上点qw的距离。

除了满足拉普拉斯方程和远前方无波的辐射条件，还在船体表面上满足物面条件，在自由液面z=ζ(x,y)上满足自由面边界条件：

式中：下标x、y、z为该变量沿x、y、z方向的偏导数，Φx为总速度势沿x方向的偏导数。

自由面边界条件可推导[2]为

式中l为该变量沿流线方向的导数。满足线性化边界条件的Bernoulli方程由船体周围的速度表达，略去φw的二阶项，船体表面无量纲化压力系数为

湿表面积无量纲化的兴波阻力系数为

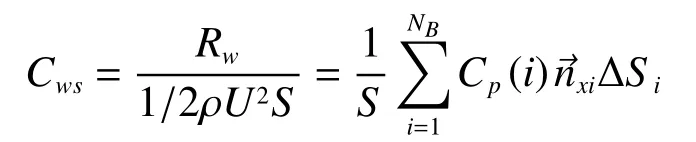
式中：ΔSi为船体离散面元的面积，S为船体湿表面积，为面元单位法向量的x方向分量。水平面波高起伏为

1.2 数值离散

为获得积分方程数值解，采用NURBS技术将船体表面和自由面离散成一系列小单元，该方法实现过程见文献[14]。如图1所示，考虑到船体具有对称性，采用半自由面和半船体进行计算。根据式(1)～式(3)边界条件，可得船体表面与自由面离散的线性方程组[14]：

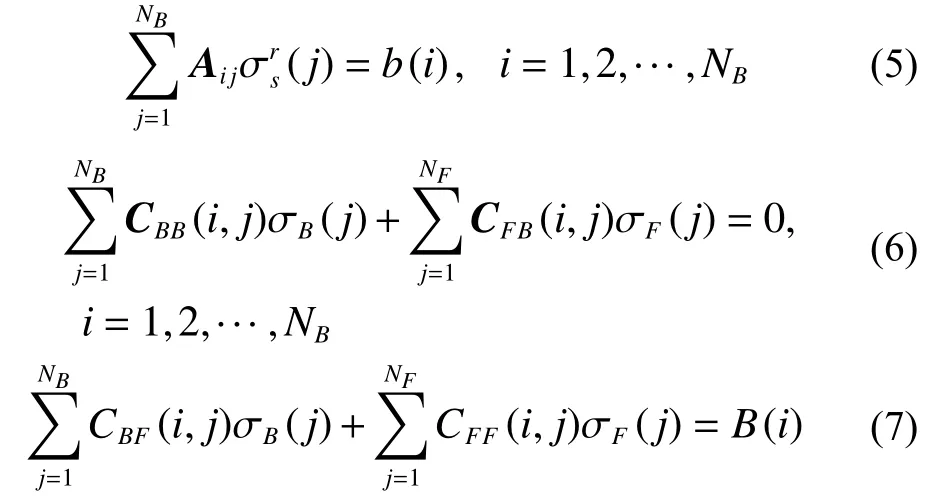
式中：NB和NF分别为半船表面和半自由面的面元数，影响系数Aij、b(i)，j=1,2,···,NF，CBB、CFB、CBF、CFF和B(i)由文献[5]提供计算方法。运用Gauss消去法可直接求解SB和SF上离散分布源的密度，进一步求解场点处兴波引起的扰动速度∇φw，最后计算出兴波阻力系数Cws和波高起伏ζ(x,y)。

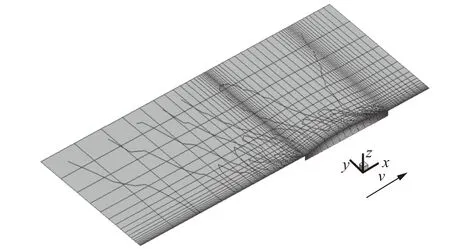
图1 计算模型示意

1.3 贴体网格

图2 自由面网格图

如图2，静水面上流线网格是通过上游点的速度追踪求得，形成了一条条流线；贴图网格是使用水线和计算域边界采用NURBS曲面[14]求得。本文Dawson法的自由面离散采用贴体网格以代替传统的叠模流线网格，进而式(4)中的Φll数值离散的过程中，二阶导数的计算转换到大地坐标系下进行。有

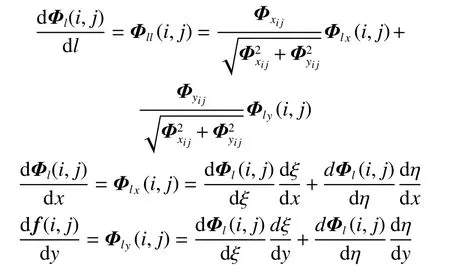
式中：(ξ，η)为物理坐标系下的点，(x，y)为大地坐标系下的点。纵向和横向的导数都采用单边上游有限差分算子：

式中J为雅可比矩阵。

Φll求出之后可以解出式(5)～式(7)中的影响系数。同时，在使用贴体网格求解的过程中，减少了使用叠模流场求解自由面离散网格这一步骤，进一步减少了兴波问题数值求解的计算时间。

2 数值计算

2.1 航行体模型

如图3和图4所示，采用2种航行体，船型参数如表1，一种是直接由数学公式来描述的Wigley船型，被广泛地用于研究常规船型的兴波问题；另一种为具有代表性的集装箱船（KRISO container ship，KCS）。采用本文开发的程序计算其兴波阻力、波高分布和船侧波高，并与相关文献的结果进行比较分析，验证该计算方法的可靠性。

图3 Wigley船型

图4 KCS船型

表1 船型参数

2.2 数值模型收敛性验证

为了研究数值模型对兴波阻力预报精度的影响，本文模拟了Wigley船型以Fr=0.3均速航行时的兴波运动，主要以航行体网格、自由面区域大小和自由面网格划分3方面关键参数进行收敛性分析。如图5～图10所示，在其他参数值不作特别说明时，取值如下：自由液面下游le=2L，自由液面上游Lf=0.5L，自由液面宽度Lw=1L，数值计算离散模型均采用非均匀网格，网格沿着各方向以系数1.1的增长率划分，船体模型网格数量NX=50，NY=20，自由液面网格数量NW=30，Ne=60，Nf=15。

2.2.1 自由面区域收敛性验证

为了对自由液面区域大小进行收敛性验证，如图5和图6所示，分别对计算域上游lf、下游le和宽度lw进行收敛性分析。从图6可以看出，当自由液面宽度lw∈[1.5L,2.2L]、上游lf∈[0.5L,1.0L]和下游le∈[2.5L,3.3L]时，兴波阻力计算结果十分接近。为了获取更高的预报精度，在下面的算例中，计算域均大小均采用le=2.5L、lf=0.5L和lw=1.5L。

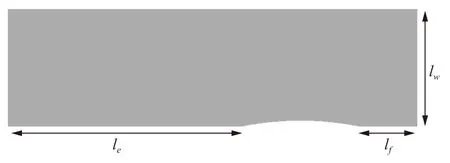
图5 自由面区域

图6 兴波阻力随自由面区域大小的变化

2.2.2 航行体网格划分收敛性验证

同上，改变Wigley船型X和Y方向网格数量进行收敛性验证，船艏艉0.2L处区域网格进行加密，如图7和图8所示，分别对船体垂向网格数NY和纵向网格数NX进行收敛性分析。从图8可以看出，NY对兴波阻力预报的结果影响较小且具有较好的收敛性，纵向网格数NX∈[50,68]时，兴波阻力计算结果具有较小波动。为了获取更高的预报精度，在下面的算例中，船体网格划分采用NX=50和NY=20。

图7 航行体网格

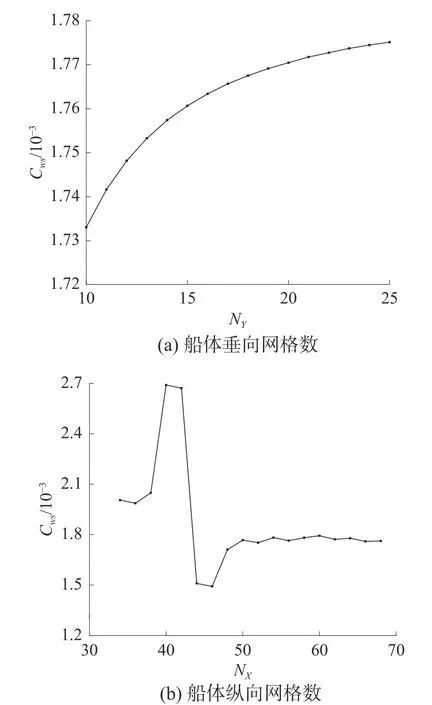
图8 兴波阻力随船体网格数量的变化

2.2.3 自由面网格划分收敛性验证

同理，对自由液面网格划分进行收敛性分析，如图9和图10所示，加密增长率Ge、Gf和Gw均为1.1。从图10可以看出，当自由液面宽度网格数较大时兴波阻力预报精度较高，而自由液面纵向网格数对计算精度波动较大，但在Nf∈[10,20]和Ne＞40时，兴波阻力计算结果十分接近。综上，自由液面网格划分采用Nw=35、Ne=40和Nf=15具 有较高的计算精度。

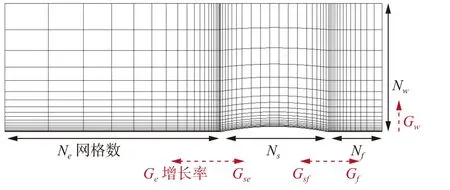
图9 自由面网格划分示意

图10 兴波阻力随自由面区域大小的变化

2.3 数值模型网格划分策略

同理，对KCS船型进行了收敛性分析，在下面的算例中，船体网格、自由面区域大小和自由面网格划分如表2。由于KCS船体曲面较为复杂，为了提高计算精度，本文采用NURBS技术[14]对艏艉进行加密，图11为船体和自由液面划分3 830个面元的计算结果，从图11中可以看出船艏艉沿纵向的网格数更为密集。

表2 计算模型数值离散网格值

图11 KCS船体及自由面网格示意

3 并行技术

C++ AMP[15]是Microsoft Corporation开发的一套C++应用程序加速技术，使用AMP并行技术编写的程序可在图形处理器（graphics processing unit，GPU）等硬件上进行计算。C++AMP的使命是将GPU编程带给每一位开发者，由于支持C++AMP的显卡没有限制，并且它包含了近乎全面的代码库，使用这些库的代码无需了解底层代码就能获得加速，这一点对于创建面向船体兴波阻力预报的代码库而言很重要。

C++AMP的“入口”即parallel_for_each (array.extent, [=] (index＜1＞ idx) restrict (amp){kernel执行体}，主要用到array容器，它用于储存加速器上同时计算的一组数据，index＜N＞用于索引指定的某个位置，其整数值N为数组维度，extent代表执行线程的数量，kernel执行体为计算函数，也是AMP的核心，为了调用函数库amp.h，必须使用restrict(amp)标记。计算环境运行在一台配置为AMD 锐龙5 3500U CPU @2.1 GHz；操作系统为Windows 10；运行内存8 GB的笔记本上。如图12，在Dawson方法的求解过程中可以在多个部分用到并行技术，主要是影响系数的计算。

图12 Dawson方法求解过程

如图13，在指定的面元数下，正常计算需要70～300 s，通过AMP方法加速计算后，基本在10～50 s左右就能算完。绿色虚线代表正常计算与AMP并行计算消耗时间的比例，总时间提速5～6倍。

图13 Dawson方法加速计算分析

4 数值方法验证

4.1 Wigley船型的兴波阻力预报

图14为以自由面横向网格数为变量的兴波阻力系数收敛图，从图14中可以看出，贴体网格的计算速度明显快于流线网格，随着面元数的增加兴波阻力系数逐渐收敛。当Fr=0.316时，如图15波高分布和图16船体吃水处波切图，从图15和图16中较为明显地看出有首尾波兴起，船体两侧出现开尔文波形，符合船体航行特征。

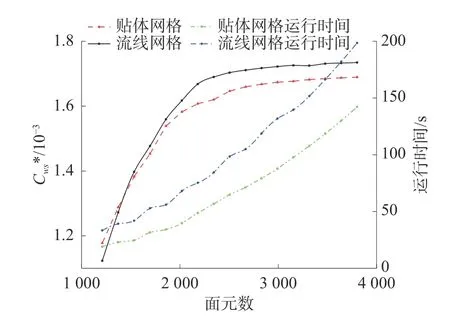
图14 不同面元数下的兴波阻力系数收敛图

图15 Fr=0.316时Wigley船型波高分布

如图17为Wigley船型兴波阻力系数随不同Fr数下航行的变化曲线，对比值来自Kim[16]和陈纪康等[17]。由图17可以看出，本文计算结果随Fr数波动趋势一致，与文献值对比有一定的差距，考虑这种差距是由网格划分的差异以及数值计算过程中本身的误差所致。针对船体近水线网格划分，采用NURBS曲面的离散精度较低，而流线网格是通过忽略黏性的叠模流场计算出来的，计算精度存在误差叠加。从本文流线网格和贴体网格程序的计算结果对比来看，后者的计算速度提升30%左右，波高的幅值较前者略大，但兴波阻力的预报结果较为接近，且贴体网格适用于方尾船型、多体船等复杂船型的兴波阻力预报[11-12]，因此采用AMP并行技术和贴体网格的结合可实现船体兴波阻力的快速预报。

图16 Fr=0.316时船体表面波切

图17 阻力计算

4.2 KCS船型的兴波阻力预报

采用本文建立的快速预报方法对KCS船型进行计算，图18为不同面元数下的兴波阻力系数收敛图。从图18中可以看出，兴波阻力系数具有较好的收敛值。当Fr为0.26和0.35时，如图19为不同航速下的船体航行波高分布图，从图19中较为明显地看出有首尾波兴起，船体两侧出现开尔文波形，Fr数越大自由面兴波起伏越大。如图20为KCS船型兴波阻力系数随不同Fr数下航行的变化曲线，其中对比值来自NM理论[3]和高阶Rankine源法[18]。可以看出，计算结果虽有些不同，但随Fr数变化较为一致，说明本文的开发程序计算结果可靠。

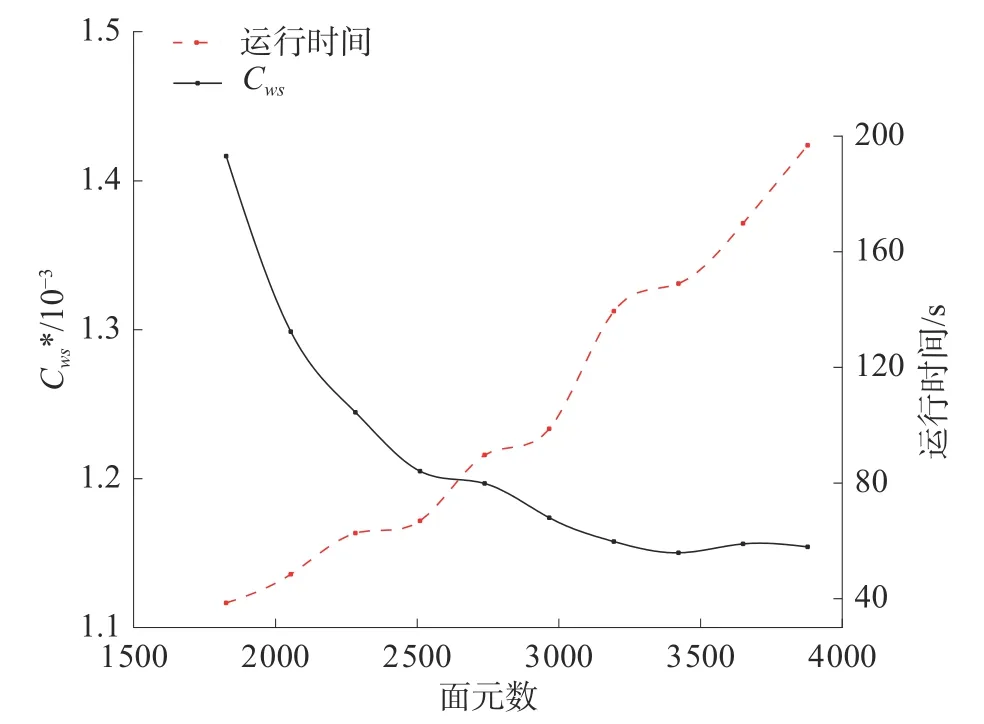
图18 不同面元数下的兴波阻力系数收敛图

图19 KCS船型波高分布

图20 KCS船型阻力计算

5 结论

本文编写了基于Dawson方法的船体兴波阻力计算程序，实现了典型船型的兴波阻力预报，并对兴波阻力的快速预报与精确求解展开研究与分析，可得出如下结论：

1）以航行体网格、自由面区域大小和自由面网格划分3方面关键参数对兴波阻力计算结果进行收敛性验证，确定了Wigley和KCS船型数值离散的网格划分策略；

2）在Dawson方法的求解过程中多处引入并行技术，采用AMP方法兴波阻力计算提速5～6倍，数十秒完成一次预报，计算效率显著提升；

3）自由面离散采用体贴网格代替流线网格，计算速度提升30%左右，波高的幅值较前者略大，兴波阻力的预报结果收敛性较好；

4）在Dawson方法中引入贴体网格和AMP并行技术，建立了船体兴波阻力快速预报方法，在两条标模船模兴波阻力的预报上取得了实效。