智能小车循迹与避障的仿真与实现

王 辉, 廖峰林,2

(1.成都大学 机械工程学院，四川 成都 610106; 2.四川新绿色药业科技发展有限公司，四川 成都 610036)

0 引 言

智能小车作为无人驾驶汽车的“缩小版”，综合了车辆工程、测控工程与人工智能等多个学科领域的相关技术，其环境适应性强，易于开发，具有广阔的应用前景[1-2].目前在实际应用中，智能小车需要解决的关键技术问题是循迹和避障的实现[3].对此，本研究采用纯跟踪算法对智能小车进行运动控制，选择适用于坐标轴或黑白地图搜寻点的A*算法对路径进行构建，通过对该算法进行优化，使得两点一线之间的连线由循迹跟踪点转变为循迹跟踪线.同时，将控制算法应用到实物智能小车中，通过超声波传感器测距与灰度传感器循迹来进行实际测试，验证了本仿真构建的智能小车运动模型、PID的参数调节、控制算法及规划出的路径的有效性.在具体测试中，实物智能小车实现了按照设定要求行走的目的.

1 智能小车的模型构建

1.1 智能小车运动模型

实际运动中的智能小车可以视为一个刚体，用其质心的空间坐标与空间姿态的6个坐标可近似描述其运动过程[4].基于此，本研究的智能小车循迹与避障主要以仿真模拟为基础，选取前轮转向后轮驱动模式，同时仅考虑智能小车的运动特性，而忽略诸如车身滑动、轮胎摩擦等动态因素.据此建立智能小车的理想运动模型，即把智能小车的运动简化为平面运动，具体构建的智能小车运动模型如图1所示，

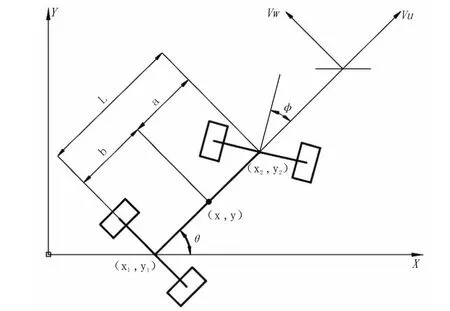
图1 智能小车运动模型示意图

图1中，设定智能小车的质心坐标为(x,y)，后轴中心坐标为(x1,y1)，前轴中心坐标为(x2,y2)，角度θ为智能小车的航向角，为车身与X轴正方向的夹角，角度φ为智能小车前轮转向角，轴距为L，前轴中心到质心长度为a，后轴中心到质心长度为b，据此，可以得到智能小车的平面运动模型方程式为，

(1)

式中，V是智能小车的速度.

1.2 基于MATLAB/Simulink仿真工具的智能小车仿真模块构建

在MATLAB/Simulink仿真工具中构建的智能小车的整体仿真模块主要由智能小车的运动仿真模块、速度仿真模块和转向角仿真模块所组成.

1.2.1 运动仿真模块

智能小车的运动模型经转换后变为运动仿真模块，具体如图2所示.

图2 智能小车的运动仿真模块

1.2.2 速度仿真模块

在建立智能小车速度仿真模拟中，由于智能小车的输入环节存在速度的变化，仿真中可能会出现振荡，因此需要添加PID控制器对其进行控制.同时，在设定车速时，需要将带动车轮旋转的电机驱动转换为速度的转换函数，从而得到智能小车的速度仿真模块，具体如图3所示，图3中，PID(s)为MATLAB/Simulink仿真工具中自带的控制模块，可以进行相关参数的调整.

图3 智能小车的速度仿真模块

1.2.3 转向角仿真模块

智能小车的转向角仿真模块同样也需要利用PID控制.由于智能小车的转向角采用平滑的曲线达到预设角度，为了使智能小车在开始有位移时能够快速动起来，其速度需要先超过预设数值再退回至预设数值，因此其需要通过PD控制来实现，具体如图4所示，

图4 智能小车转向角第一模块

此外，智能小车在转向时通常会引起较大的惯性，对此需要添加一阶惯性环节作为转向角的第二模块，具体如图5所示.

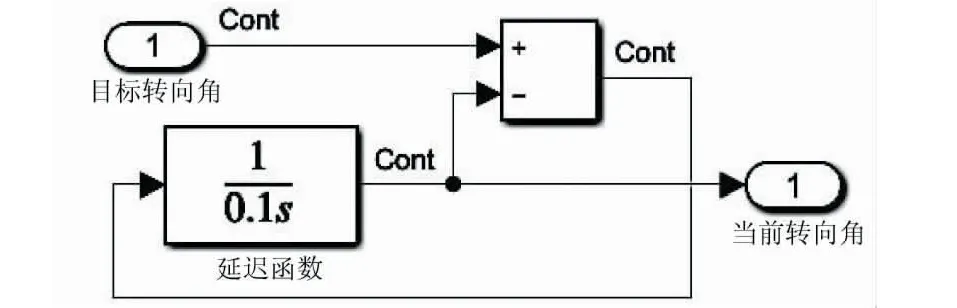
图5 智能小车转向角第二模块

1.2.4 智能小车整体仿真模块

把智能小车的运动仿真模块、速度仿真模块、转向角仿真模块与输入输出模块连接起来，最终得到智能小车的整体仿真模块，具体如图6所示.

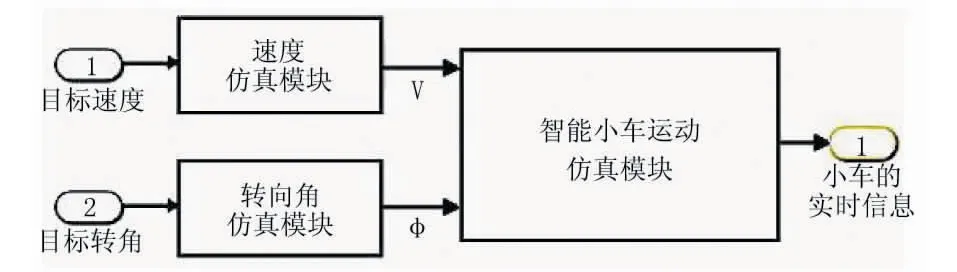
图6 智能小车仿真模块的整体构架示意图

图6中，输入为智能小车的目标速度V和目标转向角φ，输出为智能小车当前所处的位置(x,y)、航向角θ、轴向速度vμ和法向速度vω以及当前智能小车的转向角φ，实现实时显示智能小车的当前位置与姿态.

2 控制算法

本研究通过选用纯跟踪控制算法对智能小车的输入参数进行控制，可以使智能小车按照设定路径运行且输入平滑、振荡减小.

2.1 纯跟踪控制算法

智能小车在行进过程中通常都是直接跟踪由一系列路径点所构成的规划路径来自动识别路线.本研究以智能小车的输入参数转向角φ为目标，选择纯跟踪控制算法，利用路径信息对智能小车的转向进行控制[5]，其基本思路是，在每个控制周期，通过前方目标轨迹上的一个点，控制智能小车当前方向盘的动作，使其产生向目标点的运动，同时反映智能小车的位置、速度、加速度与时间变化的关系.其具体原理如图7所示，

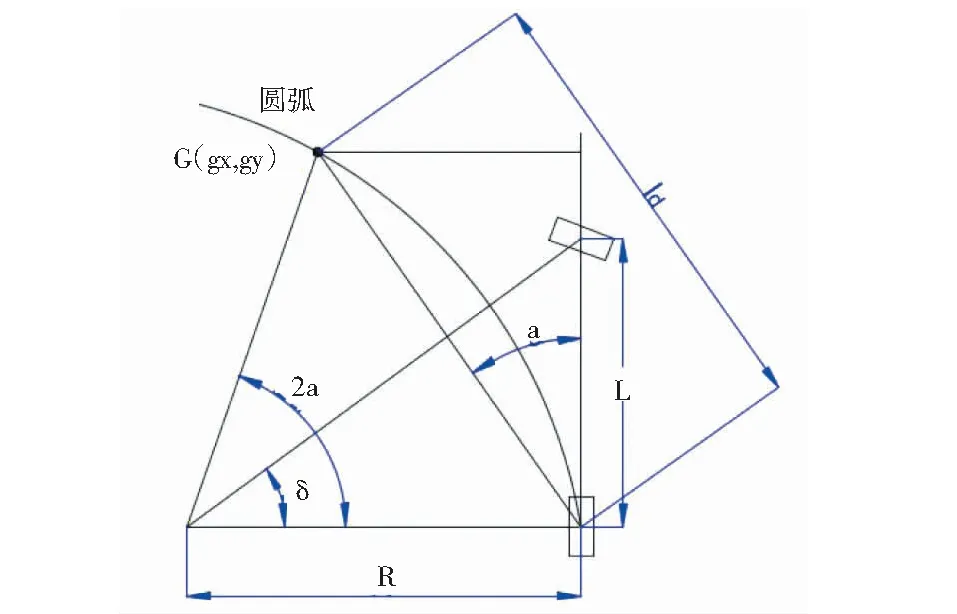
图7 纯跟踪控制算法示意图

图7中，R是智能小车的转弯半径；L是智能小车的轴距；δ是智能小车的前轮转角；α是智能小车车身与预瞄点的夹角；G(gx,gy)是智能小车在轨迹上的预瞄点；ld是智能小车的预瞄距离，用于在前方循迹的引导线上选择某个期望点[6]；圆弧表示智能小车的目标轨迹.

将纯跟踪控制算法化简后得到其计算式为，

δ(t)=arctan(2L*sin(a(t))/ld)

(2)

2.2 寻找预瞄点

在本研究中，纯跟踪算法中的预瞄点是智能小车下一个需要到达的地方.而在MATLAB仿真软件中，预瞄点的实现可通过修改代码为寻找最近点来实现.预瞄点的计算方法为：设定当前智能小车的位置坐标为(x1,y1)，其他目标的坐标为(x2,y2)，d为其他目标点到当前坐标点的距离，其计算式为，

(3)

将计算得到的距离d进行对比分析，并选择最小的距离d，然后将对应的坐标点输入至预瞄点，即获得下一个需要到达的坐标点.

2.3 PID控制

智能小车避障最关键的技术是控制好智能小车行驶的方向和速度.PID控制具有鲁棒性强的特点，因而在工业工程过程控制中被广泛地应用.PID控制的计算式为，

(4)

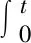
1)本研究智能小车的输入速度在PID控制的前后对比如图8所示，

图8 智能小车速度PID控制前后对比

图8中，虚线为PID控制调节前的速度输入，实线为PID控制调节后的速度输入.在1 s时输入速度设定为1 m/s.由图8可以看出，在PID控制调节前速度输入偏大，在接近3 s时稳定，而PID控制调节后输入速度为设定的1 m/s速度，在接近2 s时输入稳定.

2)智能小车的输入转向角在PID控制前后的对比如图9所示，

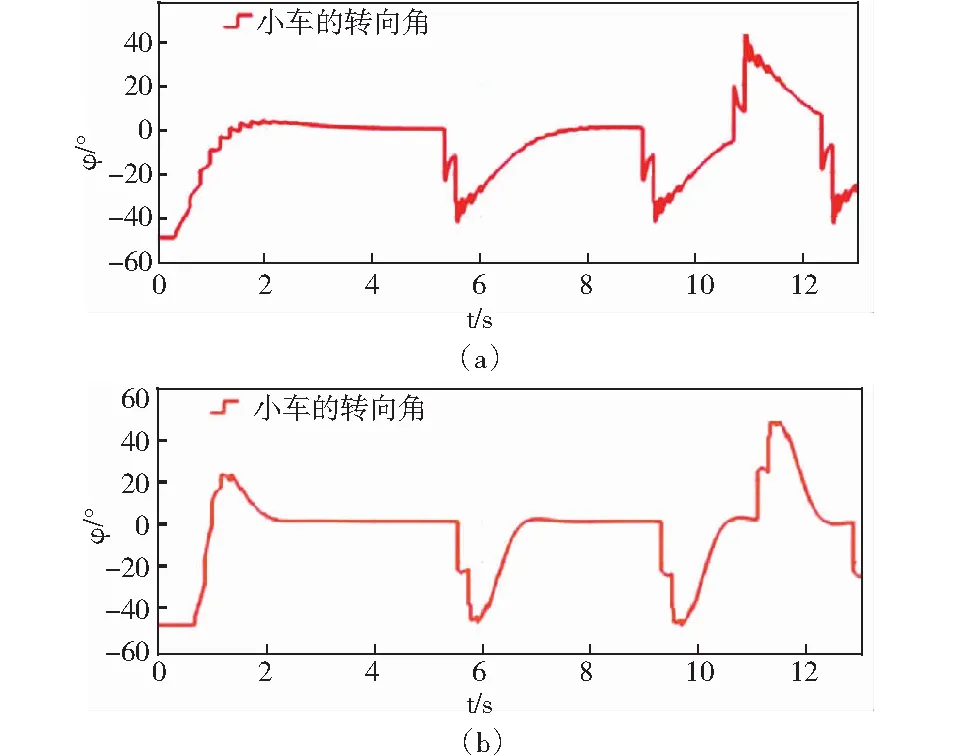
图9 转向角的PID控制前后对比

图9中，图9(a)为没有PID控制调节的转向角输入，图9(b)为有PID控制调节的转向角输入.通过对比可以看出，PID控制调节后的转向角输入平滑稳定，且振荡较小.

3 地图与路径构建及优化

3.1 地图构建

利用MATLAB仿真工具的矩阵数据可构建costmap地图.即将坐标地图显示成栅格化地图[7].在本研究中，地图坐标中含有障碍物、可行区域、起始点及目标终点，具体如图10和图11所示，

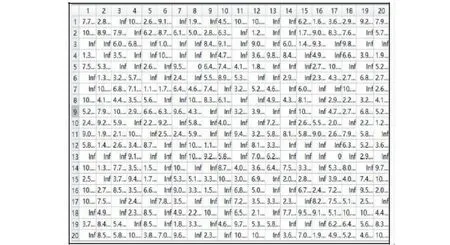
图10 矩阵数

图11 cotsmap地图

图10中，有数据的地方为可行区域，Inf表示障碍物，0表示起始点及终点.

图11为转换后的cotsmap地图，其上障碍物的位置与图10矩阵中障碍物的坐标一一对应.由于图中的障碍物数据是变化的，所以每次生成的地图也是变化的，而障碍物的比例是设定的，故障碍物的方格在每次的数量是一致的.

3.2 路径构建及优化

路径构建即是避开障碍物寻找一条或者多条可行性的道路，本研究的路径构建采用A*算法，其基本思路是：首先，设定2个空矩阵：一个命名“道路”，一个命名“距离”；然后，对所生成的地图矩阵进行搜寻，将搜寻过程中遇到的可行性路径坐标放入“道路”矩阵之中，并将该点和目标点的距离放入“距离”矩阵之中，在起始点到终点之间一直循环该步骤，直到寻找到目标点位置后跳出循环；第三，跳出循环后，对“距离”矩阵进行各点比较，直到距离为“0”，即寻到了目标点为止；最后，得到这一系列点之后，再从目标点出发，寻回至初始点，得出路径中每一个点是如何由上一个点寻找出来的，再将各点连成线，即可得到该地图中搜寻出来的一条由起始点到终点的路径.本研究依据此思路搜寻得出的路径如图12所示.

图12 地图路径构建

本研究利用A*算法搜寻出的地图路径各点坐标及对该路径优化后的部分坐标对比结果如图13所示，

图13 路径构建及优化

图13中，左边为A*算法搜寻出来的路径坐标、右边为优化后的部分路径坐标，横向1、2表示(x,y)坐标，纵向1～21表示从起始点到目标终点搜寻出来并按顺序得到的各点坐标.

4 智能小车仿真运行

智能小车与路径的匹配度，不仅可以检验智能小车的控制算法是否有效与运动模型建立是否匹配，还可以判断所获得的路径是否适用.由于避障路径的分度值为m，本研究设定的智能小车的车身长度仅为0.2m，故控制算法向前搜寻的范围仅有0.25 m.这就意味着，智能小车不能够完全看清范围点内的位置而导致搜寻点失败.对此，本研究的解决方法是将得出的路径分度值变小，并将优化后的路径坐标重新部署到智能小车的跟踪地图之中，可以发现路径中的坐标点之间的距离变小了，而路径的长度没有变化.将搭建好的智能小车模块在有规划出路径的地图中进行循迹与避障仿真运行，其仿真运行轨迹如图14所示，

图14 智能小车仿真运行轨迹

图14中，红线为智能小车运行轨迹，蓝线为规划出来的路径，可以看出智能小车在循迹避障过程中能够按照设定的路径运行，只有在直角拐弯时，会出现不重合情况.这是因为智能小车设定转向是由前轮转向角来控制，因本研究的智能小车前轮最多可以转向50°，导致其在直角转弯时不能按照直角路线行走，而是按照圆弧路线行走.

智能小车仿真运行的实时数据如图15所示，

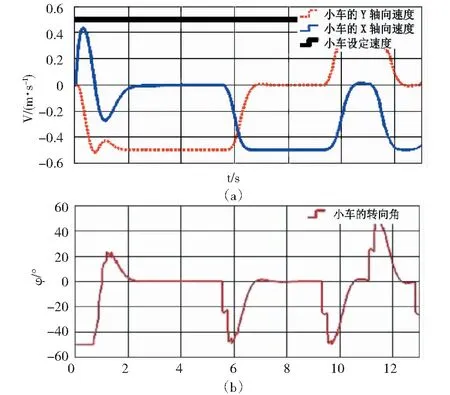
图15 智能小车仿真实时数据

图15中，图15(a)显示智能小车的实时速度,其中，黑色的线为智能小车的最大速度，设定值为0.5 m/s，蓝色的线为智能小车的X轴向速度，红色的线为智能小车的Y轴向速度.当智能小车以45 °方向行走时，速度为恒定值.由红色的线与黑色的线交点可以得知智能小车此刻的车身朝向，X轴向速度在向负值变化，Y轴向速度在向正值变化，说明智能小车在向车头的左侧转弯行驶.图15(b)显示智能小车实时转向角，正值为向左转弯，负值为向右转弯，而最大转角则和之前设定的一样为50 °.由图15的智能小车仿真实时数据与图14的智能小车行进轨迹对比可知，本研究的智能小车构建的运动模型、控制算法、设定轨迹与实际运行状态一一对应，即创建的各个模块合理、有效.

5 智能小车实车测试

本研究的智能小车实车采用差速轮运行及转向，构建的控制算法模型转换为C语言[8]嵌入其中，并采用灰度传感器及超声波传感器进行循迹与避障.灰度传感器的作用是使智能小车循着黑线运行，超声波传感器则感应前方是否有障碍物及判定障碍物的距离.在实际测中，将静态地图的路径探索转换为在地面铺设的轨迹.铺设的轨迹可以作为分度值趋近于0的坐标点，使得智能小车能够有路径可以跟踪.在智能小车的车头布置了4个灰度传感器，将仿真中的纯跟踪算法以传感器的感应来表示.

本研究智能小车实车循迹的思路为：设定智能小车的4个灰度传感器的顺序以沿着智能小车车头方向从左后、左前、右前、右后的顺序依次为1、2、3、4.当传感器2和3感应为黑且传感器1和4感应为白时，智能小车向前行；当传感器2感应为黑且传感器1、3和4感应为白时，智能小车轻微左转，此时，左轮电机转速降低，右轮电机转速不变，直到传感器2和3感应为黑，1和4感应为白时左右轮电机转速恢复相等，继续前行；轻微右转同理；当传感器1和2感应为黑时且传感器3和4感应为白时，智能小车向左大转弯，左轮电机减速，右轮电机加速，直到传感器2和3感应为黑且传感器1和4感应为白时继续前行；当4个传感器均感应为黑时，智能小车停止运行.智能小车实车测试结果如图16所示.

图16中，图16(a)是智能小车正常循迹的过程，图16(b)是智能小车遇到障碍物躲避的过程，图16(c)是智能小车躲避障碍物后重新进行循迹，回到正常路线上来的过程.

图16 智能小车循迹与避障实物测试示意图

6 结 论

本研究通过建立智能小车的运动模型，并基于MATLAB/Simulink分析工具进行了仿真模拟，完成了对仿真中智能小车控制算法的选型及优化，使智能小车在仿真中能按照设定路径运行，确定了仿真中智能小车的避障算法，完成了仿真所需要的对智能小车速度及转向角的PID控制参数调整及确定，使仿真中的智能小车轨迹能够与设定轨迹相吻合.

同时，本研究对构建的智能小车实车进行了相关测试，结果验证了本智能小车控制算法的有效性.