基于EEMD-SSA-LSSVR的短期交通流预测

李俊?胡婷

摘  要：为了提高物流的配送效率，寻求合理的配送路径，通过分析短期历史交通流量，使用集合经验模态分解去噪，以拟合优度最大化为目标，运用麻雀搜索算法优化惩罚参数和核函数参数的最小二乘支持向量机回归预测短期交通流。结果表明集合经验模态分解能有效去除短期交通流中的噪声，构建的EEMD-SSA-LSSVR模型可以高效地预测短期交通流量。

关键词：麻雀搜索算法;集合经验模态分解;短时交通流预测;最小二乘支持向量机回归

中图分类号：TP18         文献标识码：A文章编号：2096-4706（2022）06-0093-04

Short Term Traffic Flow Prediction Based on EEMD-SSA-LSSVR

LI Jun， HU Ting

（School of Business Administration， Chongqing Technology and Business University， Chongqing  400067， China）

Abstract： To improve the distribution efficiency of logistics and find the reasonable distribution route， the ensemble empirical mode is used to decompose noise signals by analyzing the short-term historical traffic flow. Aiming at maximizing the goodness of fit， the sparrow search algorithm is used to optimize the least squares support vector machine regression of penalty parameters and kernel function parameters to predict the short-term traffic flow. The results show that the ensemble empirical mode decomposition can effectively remove the noise in the short-term traffic flow， and the constructed EEMD-SSA-LSSVR model can effectively predict the short-term traffic flow.

Keywords： SSA; EEMD; short term traffic flow prediction; LSSVR

0  引  言

交通状况直接影响着车辆的行驶速度，因而间接影响着物流的配送效率。本文在时变路网下冷链低碳物流路径优化研究和重庆市物流发展水平与农业现代化测度及其时空耦合协调研究这两个课题中，发现道路交通流预测对路径优化和区域经济发展至关重要。因此本文使用麻雀搜索算法优化最小二乘支持向量机回归的参数以提高交通流预测准确度。

1  模型构建

1.1  集合经验模态分解

集合经验模态分解（Ensemble Empirical Mode Decomposition， EEMD）是由Wu等[1]在2009年提出的一种噪声辅助数据分析方法。EEMD首先将白噪声wj（d）引入到初始数据I（d）中，如式（1）。其次对含噪数据Ij（d）进行分解得到第j个本征模函数（intrinsic mode function， IMF）集。在EEMD的第j轮分解过程中，带噪的Ij（d）被分解为IMFsj，k（d）和残差rj，k（d），如式（2）。当完成N轮分解后，求解N组IMF的平均值獲得最终IMF集，如式（3）所示：

Ij（d）=I（d）+wj（d）（1）

（2）

（3）

其中，j表示第j次分解，满足0（4）

1.2  最小二乘支持向量机回归

对于一个给定的学习样本集，，利用非线性映射φ把数据集从输入空间映射一个高维特征空间，以使输入空间中的非线性拟合问题变成高维特征空间中的线性拟合问题[2]。高维特征空间的线性回归函数如式（5）所示。式中，w为权值矢量，b为偏置。

f （x）+wTφ （x）+b（5）

LSSVM选择误差ξi的二次项，优化问题和约束条件为：

（6）

St.yi=wTφ（xi）+b+ξi，i=1，2，…，l （7）

式（6）中，ξi表示误差，C为容错惩罚因子，定义Lagrange函数：

i=1，2，…，l （8）

根据库恩-塔克（KKT）条件可得：

，，αi=Cξi，（9）

消去变量w和ξ可得到如式（10）的线性系统。式中，lv=[1，…，1]T，Ωij=φT（xi）φ（xj）。

（10）

采用最小二乘法求解上面的线性方程组得到回归函数为：

（11）

引入核函数K（x，xi）=φT（x）φ（xi），则LSSVR回归模型见式（12）：

（12）

本文K（x，xi）选取径向基函数。

2  算法设计

麻雀搜索算法（Sparrow Search Algorithm， SSA）由Xue等在2020年提出[3]。算法中麻雀分为发现者和加入者，发现者负责搜索食物和为加入者提供方向，加入者利用发现者提供的信息获取食物。麻雀可以在这两种身份之间相互转换，但发现者和加入者的比例不变。

假设在d维空间中存在n只麻雀，第i只麻雀的位置为Xi=[xi1，xi2，…，xid]，i=1，2，…，n，xid为第i只麻雀在第d维空间中的位置。f（Xi）=f（[xi，1xi，2…xi，d]）为麻雀i的适应度，其中f（）为适应度函数。在算法迭代过程中，发现者的位置更新方式如式（13）所示。

（13）

t为当前迭代次数，维度j∈[1，2，…，d]，为t次迭代中麻雀i在j维的位置，T为最大迭代次数，随机数Q服从正态分布，L为1×d的矩阵，随机数α∈（0，1），预警值R2∈[0，1]，安全值ST∈[0.5，1]。R2ST表示一些麻雀已经发现了天敌，并发出了警报，此时所有麻雀需迅速向安全区域移动。

（14）

加入者的位置更新方式如式（14）所示。为在第t次迭代中全局最差位置，1×d的矩阵A中每个元素随机赋值1或-1，A+=AT（AAT）-1。为t+1次迭代中发现者的最优位置。当i>n/2时，适应度值较低的加入者i处于十分饥饿的状态，需要飞往其他地方觅食。

当麻雀发现天敌时会发出报警信号，这些麻雀的位置在种群中随机产生，如式（15）所示：

（15）

为第t次迭代中全局最优位置，步长控制参数β为服从正态分布的随机数，随机数K∈[-1，1]表示麻雀移动方向同时也是步长控制参数，fi为麻雀i的适应度，fw为当前全局最差适应度值，fg为当前全局最优适应度值，ε为极小常数。fi>fg表示麻雀处于种群边缘，易受天敌攻击。fi=fg表明处于种群中间的麻雀意识到了危险，需要靠近其他麻雀以减少被捕食的风险。SSA-LSSVR短期交通流预测的适应度函数为拟合优度，如式（16），其中yi为真实值，为预测值，为均值。算法流程图如图1所示。

（16）

3  短期交通流预测

交通数据来自明尼苏达州交通部数据研究实验室（http：//www.d.umn.edu/～tkwon/TDRL-Software/Download.html）。数据是位于I-35W上S64站点的341号、342号和343号探测器2016年1月1日至2016年1月15日（15天）的平均值，站点位置如图2所示。数据每隔5分钟测量一次。数据集分为训练集和测试集，分别为14天和1天。实验采用PyCharm IDE编程，在Windows11 X64操作系统、AMD Ryzen 75800H CPU、16 GB内存环境下运行。本文麻雀种群规模为30，迭代次数为50，发现者比例为20%，预警麻雀比例为10%，预警值为0.6。

3.1  数据预处理

3.1.1  时序相空间重构

设时间序列数据为[T1，T2，…，Tn]，建立滑动窗口如式（17）所示，参考文献[4]，本文m=5。

，（17）

3.1.2  数据标准化

由于LSSVR的假设建立在数据集是正态分布的基础上，因此采用Z-score规范化，将原始交通流映射到均值为0，标准差为1的分布上，见式（18），其中μ为均值，δ为方差[5]。

z=（Xi-μ）/δ（18）

3.2  集合经验模态分解

采用EEMD分解得到的IMF函数如图3所示。根据波动频率和瞬时频率，将IMF1和IMF2作为噪音去除，将IMF3-11求和重构为去噪交通流。以2016年1月15日的交通流为例，由图4可知，去噪后的交通流曲线更加平滑。

3.3  预测结果比较

四种模型的预测结果如表1所示，预测效果如图5至图8所示。使用默认参数的LSSVR预测原始交通流，拟合优度R2为0.776 07。使用SSA优化LSSVR的惩罚系数C和核函数参数gamma预测原始交通流，拟合优度R2增加，均方误差MSE减小，拟合效果提高。优化后的惩罚系数C和核函数参数gamma分别为0.286 000 42和0.212 426 08。SSA-LSSVR的收敛曲线如图9所示，发现收敛曲线呈阶梯型，SSA在第12代收敛。

为降低噪声对预测的影响，使用EEMD对原始交通流去噪，再使用LSSVR预测去噪后的交通流，拟合优度R2为0.996 78。相比原始交通流预测，去噪后的预测效果明显提升。最后，使用SSA优化LSSVR的惩罚系数C和核函数参数gamma预测去噪后的交通流，拟合优度R2增加，为0.996 93;均方误差MSE减小，为0.034 47，进一步提高了LSSVR的预测效果，优化后的惩罚系数C和核函数参数gamma分别为18.939 801 07和0.652 176 03。

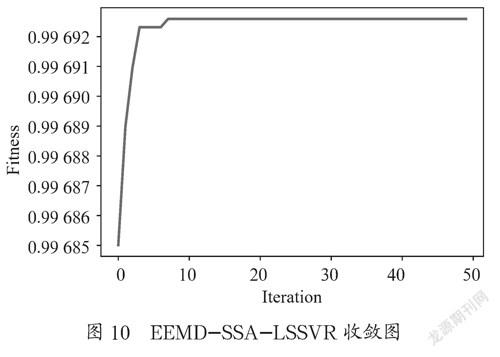
SSA-EEMD-LSSVR的收敛曲线如图10所示，发现SSA在第8代收敛，相比原始交通流预测，去噪后算法收敛速度更快，寻优精度更高。

4  结  论

针对短期交通流非线性、含噪性的特点，本文使用集合经验模态分解去除短期交通流中的噪音，提高了短期交通流预测的准确率;其次，本文使用麻雀搜索算法優化最小二乘支持向量回归的惩罚参数和核函数参数，可以减少试参的盲目性并提高模型预测的精度。

参考文献：

[1] WU Z H， HUANG N E. ENSEMBLE EMPIRICAL MO DEDECOMPOSITION：ANOISE-ASSISTED DATA ANALYSIS METHOD [J].Advances in Adaptive Data Analysis，2009，1（1）：1-44.

[2] SUYKENS J A，VANDEWALLE J，MOOR B D. Optimal control by least squares support vector machines [J].Neural Networks，2001，14（1）：23-35.

[3] XUE J K，SHEN B. A novel swarm intelligence optimization approach：sparrow search algorithm [J].Systems Science & Control Engineering，2020，8（1）：23-24.

[4] 曹成涛，徐建闽.基于PSO-SVM的短期交通流预测方法 [J].计算机工程与应用，2007（15）：12-14.

[5] ZHANG Q Y，QIAN H，CHEN Y P， et al. A short-term traffic forecasting model based on echo state network optimized by improved fruit fly optimization algorithm [J].Neurocomputing，2020，416：117-124.

作者简介：李俊（1998—），男，汉族，江西九江人，中级物流师，硕士研究生，研究方向：智能算法;胡婷（1996—），女，汉族，四川遂宁人，硕士研究生在读，研究方向：智能算法。

收稿日期：2022-02-09

基金项目：重庆工商大学研究生创新型科研项目（yjscxx2021-112-14、yjscxx2021-112-15）