考虑流固耦合效应的漂浮物撞击平面钢闸门的研究

刘江川, 李晓东，朱茂源

(长春工程学院 水利与环境工程学院，吉林 长春 130012)

水工钢闸门作为防洪、排涝和水资源利用工程中的重要结构物，闸门的安全运行将直接影响整个水利枢纽的安全运行，一旦闸门结构发生破坏将会严重威胁下游居民的生命财产安全[1]。流体与闸门结构二者之间组成两个存在相互作用的系统，当闸门开启时，流体本身所储存的势能转化为动能，与闸门结构发生相互作用时，将其携带的动能的一部分传递给闸门结构，从而导致闸门发生震动；同时振动的闸门反作用于流体，改变流体原有的流动状态，称这种现象为激流振动[2]。在水流作用下，闸门可能受到静荷载、动水荷载、漂浮物撞击荷载以及由风场产生的波浪荷载作用。其中闸门在动水作用下产生振动而引起的动水荷载和漂浮物撞击闸门而产生的漂浮物撞击荷载[3]的影响最大，流速较大的洪水及其携带的漂浮物会对闸门产生很大的冲击作用，是引起闸门结构失稳破坏一个主要原因。目前对闸门主要研究方向为闸门和水流的流固耦合所导致的闸门流激振动问题，国内外学者对此展开了大量的研究，并取得了丰厚成果。物理模型实验法[4]：通过电压式加速传感器以及振动信号采集系统，得到不同来流情况与平板闸门振动的关系；数值模拟计算法[5]：通过对不同开度下闸门流激振动情况的数值模拟，得到了闸门不同开度下的位移、应力情况；物理模型实验和数值模拟相结合法[6]：通过巴塘水电站导流洞平面闸门流激振动试验和ANSYS Workbench数值模拟相结合的方法，得出闸门的流激振动响应特性。关于闸门泄流时，水流携带的漂浮物撞击闸门的研究鲜见，漂浮物撞击对闸门结构的影响的研究有待于深入。

为此，借助ABAQUS软件建立水流场-闸门-漂浮物数值模型，研究了考虑流固耦合效应下的漂浮撞击对开启的平面钢闸门的影响。

1 漂浮物撞击平面钢闸门理论

1.1 流固耦合理论

考虑动水质量对闸门结构的影响，其在坐标系中的动力平衡方程为[7-9]：

[М] {W}+[C] {W}+[K] {W}={Fs(t)}+{Fg(t)}

(1)

式中：[М]、{W}、[C]、[K]、{Fs}、{Fg}分别为质量矩阵、结构的节点自由度、阻尼矩阵、刚度矩阵、由流场附加产生的压力和由其它荷载附加产生的压力。其中{W}由流固耦合面的自由度[Ws]，流固耦合面以上的自由度[Wg]组成，其表达式为：

{W}=[[Ws]T×[Wg]T]T

(2)

{Fs}可改写为：

{Fs}=-[Mg]×{W}

(3)

其中：[Мg]为附加质量矩阵，对于流固耦合问题此处附加的介质为“水”。

推导得：

([M]+[Mg]){W}+[C]{W}+[K]{W}={Fg(t)}

(4)

实际工程中闸门结构会因动水冲击发生自由振动，此时荷载向量为0且可以不考虑结构阻尼对闸门自振的影响[9]，式(4)可改写为：

([M]+[Mg]){W}+[K]{W}=0

(5)

式(5)即为闸门结构在动水冲击作用下闸门的振动方程。

1.2 Heins-Derucher碰撞理论

利用能量守恒定律将漂浮物和闸门作为研究对象，假定发生完全非弹性碰撞并且考虑流体和摩擦的影响，建立总能量方程[10]：

E=E1+E2+E3+E4

(6)

式中：E、E1、E2、E3、E4分别为碰撞前的系统总能量、漂浮物碰撞后的变形能、碰撞后闸门的变形能、漂浮物得回弹势能、摩擦势能。

当漂浮物与闸门发生完全弹性碰撞时，能量全部转化为闸门的变形能，此时闸门变形最大，能量方程为：

E=E2

(7)

为了简化碰撞模型的多种变量的复杂工况，基于能量守恒原理，引入弹簧数学模型并结合交换理论来研究碰撞问题。即将漂浮物碰撞闸门简化为弹簧体系，建立如下方程：

(8)

Fmax=KXmax

(9)

amax=V0λt

(10)

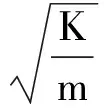
2 计算模型

2.1 工程概况

某水库枢纽主要建筑物包含：挡水建筑物、泄洪建筑物、放水建筑物。其中泄洪建筑物为正常溢洪道，位于大坝中部，分二级消能；一级消能由泄洪闸控制段、陡坡、消力池组成，泄洪闸共3孔，孔口尺寸为2 m×6 m(宽×高)，闸底板高程19.50 m，正常蓄水位22.5 m，汛限水位22.5 m；二级消能由溢流控制段、陡坡、消力池组成，溢流堰为钢筋混凝土结构，溢流宽度8.5 m，二级消能堰顶高程16.3 m，一、二级消能由35 m长泄洪渠相连。

2.2 计算模型及网格划分

通过查阅相关文献资料发现闸前流场对闸门结构的影响较大[11-12]。本文包含两组有限元模型分别为：流固耦合模型和漂浮物撞击耦合模型，其示意图如图1、图2所示。流体域由闸前和闸门开启时的闸下流体域组成，固体域包含漂浮物(以圆木为例)和闸门(闸门开度为0.5 m)。对其进行网格划分，流固耦合模型结点总数为29 996个，单元总数为24 910个；漂浮物撞击模型结点总数为34 892个,单元总数为28 886个。闸门跨度方向为x向，闸门高度方向为y向，上游至下游的流向方向为z向，闸门受到跨度方向，水流上游方向及闸门底部的水流的约束。

图1 流固耦合模型

图2 漂浮物撞击模型

2.3 流固耦合及碰撞的接触设置

将闸门与流体域的接触面设置为流固耦合面，流场域除进出口面以外均设置为壁面条件。流场向结构场传递力，结构场向流场传递位移。漂浮物与闸门的碰撞常用计算方法有：流固耦合方法[13],附加质量法[14]。流固耦合方法通过对撞击物周围的流场变化过程的计算，真实地体现出碰撞的情况，得到漂浮物撞击对闸门结构的影响，但该方法将会极大的增加计算量且精确的结果需要庞大的网格基础进行支撑。附加质量方法通过增加漂浮物的密度来附加水流的影响效果，该种方法的弊端在于附加质量的精确附加量无法确定[15]。两种方法均存在一些不足之处，本文在考虑流场和闸门之前流固耦合效应的基础上[16]，将漂浮物定义为刚体，其速度为最大流场速度的1/3。

3 有限元计算结果分析

3.1 流场水动力分析

3.1.1 流场最大流速变化分析

流场的最大流速首先出现于闸前的闸门开启部位，而后逐渐向闸门底缘移动。闸门开启时闸前最大流速的变化规律为：最大水流速度随着闸门的开启时间增加而呈现逐步减小的趋势，前期降幅明显，中后期整体呈波浪式减小趋势，减小幅度相对较小。闸前最大流速Vm的时程曲线如图3所示。

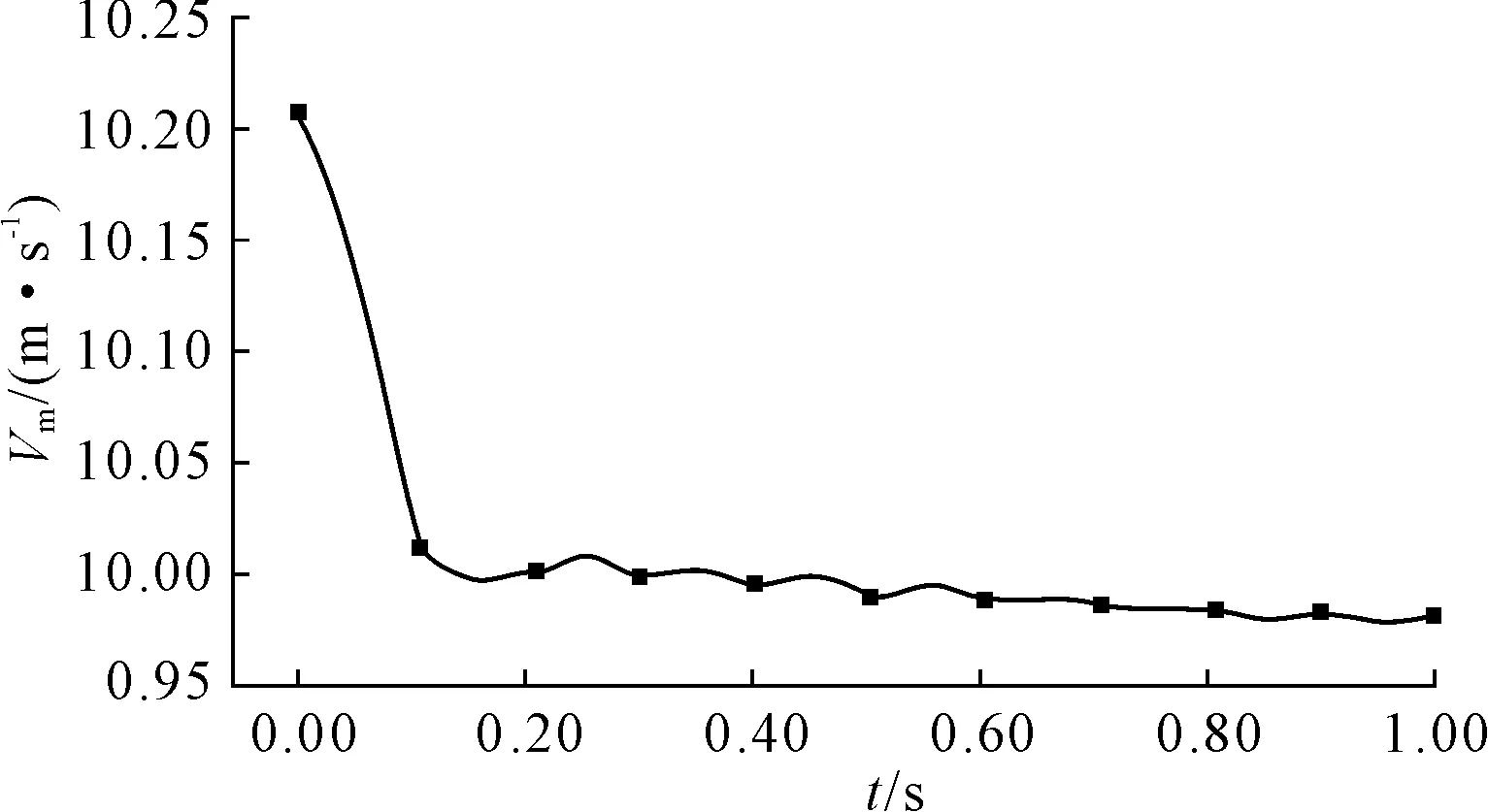
图3 闸前最大流速Vm的时程曲线

3.1.2 流场位移分析

水面线是溢洪道等泄水建筑物的重要设计参数，计算方式为体积比函数的50%时的水气交界面。当比值为0时表示该泄水建筑物中无水体存在；当比值为0～1之间时，表示该泄水建筑物存在水气交接面；当比值为1时，表示该泄水建筑物充满水体。

图4为闸前流场的横向位移剖面云图，当闸门开启时流场的最大位移位于闸门挡水侧中央位置。流场位移的分布情况为自远处至挡水面较近处位移变化相对较小，至临近挡水面处位移迅速增大至最大值。流体域的最小位移位于闸门挡水面边缘附近，为泄流时闸前出现漩涡和涌浪等现象所致。

图4 流体域的位移x剖面云图

3.1.3 流场压力分析

闸门未开启时流场未发生流动，其水压力为静水压力，当闸门刚开启时，流体域距闸门较远处水流的流动相对较小可视作静水压力。闸门底缘下方及其周围距离较近位置的流场流动性较大，此处水压力为动水压力，水压最大值由闸门底缘前方逐渐向闸门底缘下方移动。一段时间后闸前流场全部发生流动，此时水压逐渐增大，其水压分布与速度分布基本一致。

3.2 闸门结构分析

3.2.1 闸门结构位移分析

图5为闸门的位移云图，闸门在水流振动作用下最大位移出现在闸门面板跨度方向中轴线处。位移由闸门面板中部逐渐向左右两侧减小，且沿闸门中线位置对称。闸门与水流流固耦合面以上部分位移量较小，约0.9 mm。

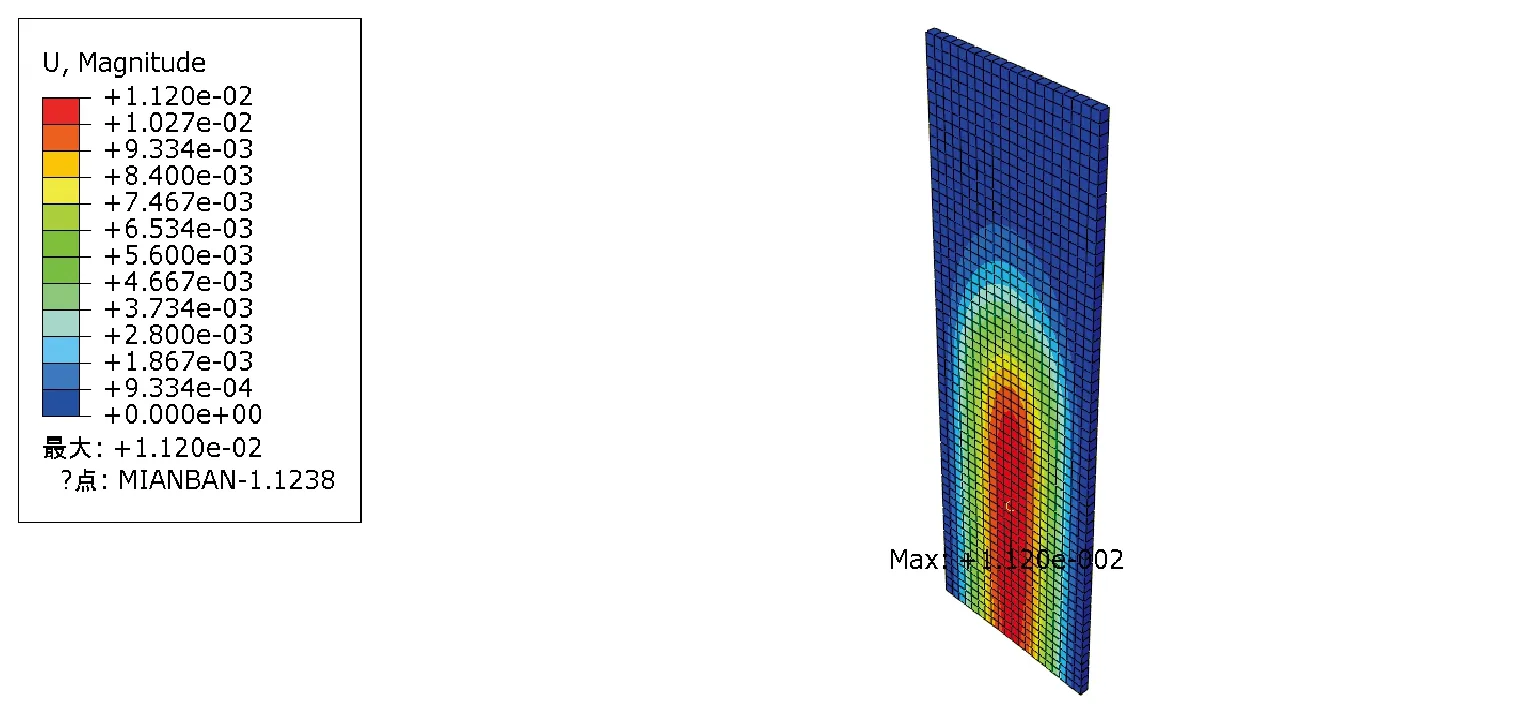
图5 闸门位移云图

图6为闸门的最大位移Um的时程曲线，从图6可知无漂浮物碰撞情况，闸门开启时为闸门位移量最大时刻，最大值为23 mm；随着闸门开启时间的增加闸门位移量逐渐趋于稳定并维持在11.2 mm附近。

图6 最大位移Um的时程曲线

3.2.2 闸门结构应力分析

图7为闸门面板的最大应力时程曲线。闸门开启前的最大应力为86.45 MPa，闸门刚开启时的最大应力为96.35 MPa，应力值瞬间增大10%，结合图7可知闸门刚开启时瞬间面板应力迅速增大，随着闸门开启时间的增加，闸门面板的最大应力首先迅速降低，而后与闸门位移的变化基本一致，在0.5 s后逐渐趋于稳定并最终稳定在24.26 MPa附近。

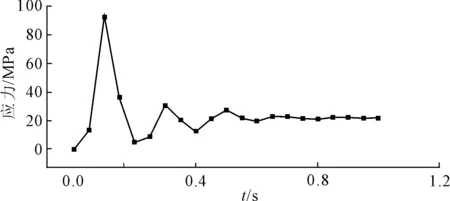
图7 面板最大应力的时程曲线

3.3 漂浮物撞击对闸门结构的影响分析

为使撞击力及撞击位移在云图上显示更加清晰，本文选择闸门中线与流固耦合面顶部的交线点为碰撞点。

3.3.1 漂浮物撞击对闸门结构应力的影响

图8、图9分别为闸门在有、无漂浮物撞击闸门面板的应力云图。从应力云图可清晰的看出有无漂浮物撞击流固耦合面以上位置应力分布基本一致，最小应力位于闸门顶端，且漂浮物撞击下的闸门面板的应力值大于无碰撞情况。对比发现，漂浮物撞击将使闸门面板的应力出现整体性的增加现象。

从图8和图9比较发现，流固耦合面以下位置应力较为集中的区域亦大致相同，其中漂浮物撞击情况的闸门面板中部出现大范围的应力集中现象，且应力值接近闸门面板应力最大值。

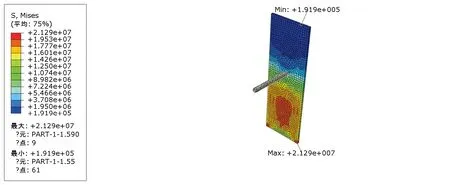
图8 有漂浮物撞击的应力云图

图9 无漂浮物撞击的应力云图

3.3.2 撞击对闸门结构位移的影响

为进一步探明水流及携带的漂浮物撞击闸门结构的动力响应情况，以撞击中心点下方0.5 m、中心点、右侧0.5 m、上方0.5 m为例研究闸门结构的位移情况。

图10曲线自上而下分别为撞击中心点下方0.5 m、中心点、右侧0.5 m、上方0.5 m的闸门面板位移时程曲线。由图10可知四个不同位置的闸门位移时程曲线的变化趋势基本相同。漂浮物自远处漂来未与闸门面板发生撞击时，位移时程曲线与前文相同。当漂浮物与闸门发生撞击后，此时各条逐渐趋于稳定的时程曲线均出现一个较小的位移增大的现象，增大幅度从小到大依次为撞击中心点、下方0.5 m处、上方0.5 m处和右0.5 m，这与上节关于漂浮物对面板闸门应力响应结果一致。

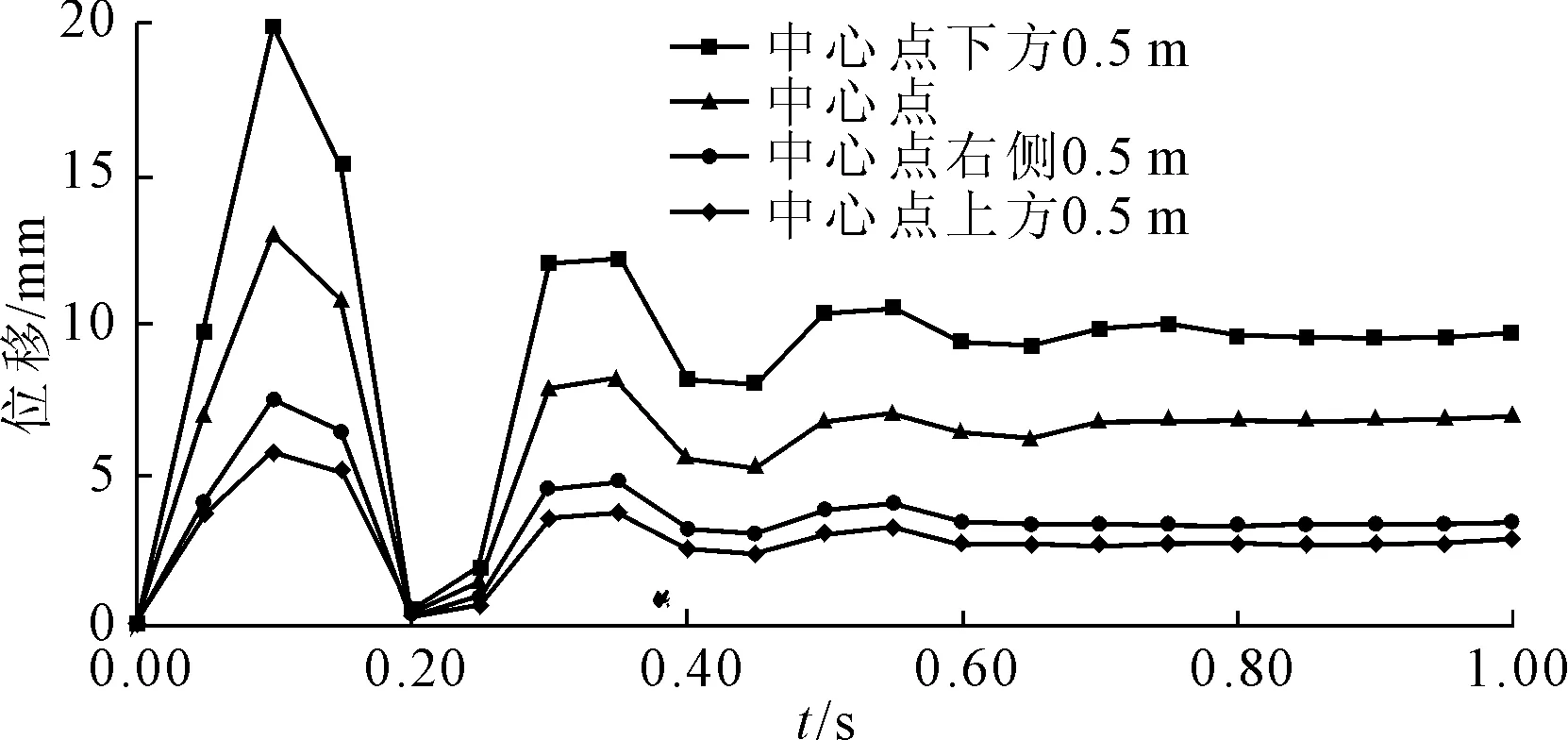
图10 撞击作用下不同点的位移时程曲线

4 结 论

本文对考虑流固耦合响应的平面钢闸门受到漂浮物撞击的动力响应分析进行研究，得到主要结论如下：

(1) 对于水流场：流场的最大流速、压力、位移均出现在闸门附近，且随着开启时间的增加逐渐向闸门底缘移动。

(2) 对于闸门结构：闸门最大应力出现在闸门面板底部两侧位置，且应力由闸门面板底部向上逐渐减小，沿着闸门面板中线呈对称分布；漂浮物撞击对闸门的影响主要表现为：闸门面板中部出现大范围的应力集中现象，且闸门面板出现整体性的应力增加现象。在工程中可以通过增加或增强该处空间梁结构的方法以达到增强闸门结构稳定性的目的。