右C-qrpp半群的性质与结构

饶冬飞，邓梓杨

(豫章师范学院数学与计算机学院，江西 南昌 330103)

在半群S中，称a为正则元，若∃x∈S使得axa=a；称S为正则半群，若半群S的元素都是正则元；正则半群S称为完全正则半群若S中任意元素a，∃x∈S使得xa=ax，它在研究正则半群的结构理论中起着重要作用。在rpp半群范围内完全正则半群的类似，Guo-Shum-Zhu[1]定义了强-rpp半群并介绍了半织积概念，证得了：一个半群是左C-rpp的当且仅当该半群同构于一个左正则带与一个C-rpp半群的某个半织积。随后，许多学者进行强-rpp半群的研究工作[2-6]。Tang[7-8]引进Green**关系L**,R**，定义并研究了C-wrpp半群。作为强rpp半群在wrpp半群范围的一般化，Du-Shum[9]定义了适当wrpp半群，研究了左C-wrpp半群的半织积结构。饶[10]定义的强qrpp半群是强rpp半群在wrpp半群范围的另外一种推广，探讨了这一半群的子类右C-qrpp半群，获得了右C-qrpp半群的一些特征。

本文是对右C-qrpp半群的进一步研究，发现它与右C-rpp半群[6]有一些相似的特征，文章的最后部分定义了对偶半织积，证得：一个半群是右C-qrpp的当且仅当该半群同构于一个C-wrpp半群与一个右正则带的对偶半织积。

1 若干准备

定义1.1[8]半群S称为左(右)K可消的：若∀a,x,y∈S,axKay(xaKya)⟹xKy，其中K是S上的一个等价关系。半群S称为K可消的：若S既左K可消又右K可消。

设S为半群，定义关系L**,R**：对于a,b∈S

aL**b当且仅当∀x,y∈S1,(ax,ay)∈R⟺(bx,by)∈R；

aR**b当且仅当∀x,y∈S1,(xa,ya)∈L⟺(xb,yb)∈L[8]

L**是S上的右同余且L⊆L*⊆L**而R**是S上的左同余且R⊆R*⊆R**。记R(+)=R,L(+)=L**H(+)=L(+)∩R(+),D(+)=L(+)∨R(+),且aJ(+)b⟺J(+)(a)=J(+)(b)[9],其中J(+)(a)是包含a，既被L(+)渗透，又被R(+)渗透的最小理想。换句话说,J(+)(a)是些L(+)类的并，也是些R(+)类的并。

定义1.2[10]称S为qrpp半群若半群S的每一个L(+)类至少含有一个幂等元；称S为强qrpp半群若qrpp半群S满足：∀a∈S，存在唯一的幂等元a+，使得a+L(+)a且aa+=a=a+a。

可以看出，适当wrpp半群[9]是强qrpp半群，一个C-wrpp半群S本质上是幂等元集E(S)是中心的qrpp半群。

定义1.3[10]称S为右C-qrpp半群，若强qrpp半群S满足：①D(+)是S上的一个同余，②对于∀e∈E(S)，Se⊆eS，③D(+)|Reg(S)=D|Reg(S)，其中Reg(S)是S的正则元集。

引理1.1[9]半群S是C-wrpp半群当且仅当半群S左R可消幺半群的强半格。

定义1.4[11]称半群B为带若B内每个元都是幂等元；称带B为右正则带若∀b1,b2∈B，b1b2b1=b2b1。注意到，一个右正则带B的每个L类仅有一个元[11]。

引理1.2[10]设S是一个强qrpp半群，以下命题等价：

(1)S是右C-qrpp半群；

(2)D(+)是S上的半格同余，且D(+)|Reg(S)=R|Reg(S)；

(3)S=∪α∈Y(Mα×Λα),其中Y为半格，且Mα是左R可消幺半群,Λα是右零带。

设S=∪α∈Y(Mα×Λα),其中Y为半格,Mα是左R可消幺半群,Λα是右零带。记M=∪α∈YMα,对M的元素定义运算⊗:

∀u∈Mα,v∈Mβ,α,β∈Y,u⊗v=w⟺∃λ∈Λα,τ∈Λβ使得(u,λ)(v,τ)=(w,k)，

其中(w,k)∈Mαβ×Λαβ。容易看出∀u,v∈Mα,α∈Y,u⊗v=uv，其中uv是u,v在Mα中的乘积。

引理1.3[8](M,⊗)是一个左R可消幺半群的强半格。

引理1.4[9]任一个半群S上都成立:L(+)°R(+)=R(+)°L(+)且D(+)=L(+)°R(+)。

命题1.1若强qrpp半群S具有半格分解:S=∪α∈YSα,其中Sα是强qrpp半群，则:

a∈Sα⟹a+∈Sα；

(2)L(+)(S)∩(Sα×Sα)=L(+)(Sα).

证明(1)令a∈Sα,∃a+∈E(S)，使得a+L(+)(S)a及aa+=a=a+a。假设a+∈Sβ,因为a+a=a,所以α≤β。Sα是强qrpp半群,故存在唯一a◇∈E(Sα)，使得a◇L(+)(Sα)a，aa◇=a=a◇a。因为aa+=a,所以(aa+,aa◇)∈R;又a+L(+)(S)a,得(a+,aa◇)∈R.于是a+a◇∈Sβ，从而α≥β。这就是说，α=β及a+∈Sα。

(2)设a,b∈Sα且aL(+)(S)b.若x,y∈S1且满足(ax,ay)∈R(Sα),则(ax,ay)∈R(S)。注意到aL(+)(S)b，于是(bx,by)∈R(S)。我们断言:(bx,by)∈R(Sα)。实际上，存在u,v∈S1使得bxu=by及byv=bx；因而bx(bx)+u=by及by(by)+v=bx；由结论(1)知，(bx)+u,(by)+v∈Sα，我们得到(ax,ay)∈R(Sα)⟹(bx,by)∈R(Sα)。反之，(bx,by)∈R(Sα)⟹(ax,ay)∈R(Sα)。于是结论(2)成立。

命题1.2设M是左R可消幺半群且Λ是右零带，则直积M×Λ是L(+)单的强qrpp半群。

证明设(a,e),(b,f)∈M×Λ，易见(a,e)R(b,f)⟺aRb。可令(x,g),(y,h)∈(M×Λ)1,且(a,e)(x,g)R(a,e)(y,h)，则axRay。由M是左R可消幺半群知：xRy。由R是个右同余，则bxRby，因而(b,f)(x,g)R(b,f)(y,h)。反之，(b,f)(x,g)R(b,f)(y,h)蕴含(a,e)(x,g)R(a,e)(y,h)。故(a,e)L(+)(b,f)，即直积M×Λ是L(+)单半群，(a,e)L(+)(1,e)蕴含M×Λ是qrpp半群。

再来证明M×Λ是强qrpp半群。易见(1,e)(a,e)=(a,e)=(a,e)(1,e)。设幂等元(1,f)满足(1,f)L(+)(a,e)且(1,f)(a,e)=(a,e)=(a,e)(1,f)，于是fe=e=ef，考虑到Λ是右零带，有f=e，故M×Λ是强qrpp半群。

定义1.5右C半群是指正则半群满足条件∀e∈E(S),Se⊆eS，其中E(S)是S的幂等元集。右C半群是左C半群[12]的对偶。

引理1.5[12](1)在右C半群中有：D=R；

(2)设S是半群，则S是右C半群当且仅当S是完全正则半群且E(S)是右正则带。

命题1.3设S是半群，若S=∪α∈Y(Mα×Λα)，其中Y为半格，且∀α∈Y,Mα是左R可

消幺半群,Λα是右零带，则D(+)|Reg(S)=R|Reg(S).

证明记Sα=Mα×Λα，幺半群的单位元1唯一，Mα是左R可消，e2=e⟹(e2,e)∈R

⟹(e,1)∈R⟹e·1=1⟹e=1，可设E(Sα)={((1α,i)|i∈Λα}，其中1α是Mα的单位元。

设a∈Reg(S)∩Sα，b∈Reg(S)∩Sβ，aD(+)b，根据引理1.4知，存在c∈S使得

aL(+)cRb；设u∈Sα，v∈Sβ，uR(S)v⟹α=β，因而c∈Sβ。可设c=(cβ,iβ)，易见

cRc(1β,iβ)。又aL(+)c，故aRa(1β,iβ)。于是α=αβ⟹α≤β。利用D(+)的对称性可得

β≤α，于是α=β。根据Reg(S)中任何两个元必有R关系，于是aRb。这就得到了

D(+)|Reg(S)⊆R|Reg(S)，由D(+)定义可知，D(+)|Reg(S)⊇R|Reg(S)，结论成立。

2 右C-qrpp半群的性质

我们来探讨一些右C-qrpp半群的性质。

引理2.1在半群S中，若∀e∈E(S),有Se⊆eS，则Reg(S)是右C半群。

证明设e,f∈E(S)，ef∈Sf⊆fS⟹∃x∈S,ef=fx=ffx=fef。于是ef·ef=e·fef=e·ef=ef，从而E(S)是右正则带。这就表明：Reg(S)是S的子半群。再由Se⊆eS⟹Reg(S)e⊆eReg(S)可知Reg(S)是右C半群。

在强qrpp半群S上，定义关系aR(◇)b⟺a+Rb+，易见：R(◇)是S上的等价关系，且R(◇)⊆D(+).

定理2.2设S是一个强qrpp半群且D(+)|Reg(S)=D|Reg(S)，则S是右C-qrpp半群当且仅当

R(◇)是S上的半格同余且∀e∈E(S)，Se⊆eS。

证明(⟹)设S是右C-qrpp半群，根据定义1.3，只需证明R(◇)是S上的半格同余。由引理1.2可设S=∪α∈Y(Mα×Λα),其中Y为半格，且∀α∈Y,Mα是左R可消幺半群,Λα是右零带。根据命题1.2知，Mα×Λα(α∈Y)是L(+)单的强qrpp半群。当我们设(a,i)∈Mα×Λα，(b,j)∈Mβ×Λβ时，会有(a,i)+∈Mα×Λα，(b,j)+∈Mβ×Λβ，于是(a,i)+=(1α,i)，(β,j)+=(1β,j)。因而(a,i)R(◇)(b,j)⟺(1α,i)R(1β,j)⟺α=β。这就表明：R(◇)=∪α∈Y((Mα×Λα)×(Mα×Λα))，即R(◇)是S上的半格同余。

(⟸)设R(◇)是S上的半格同余且∀e∈E(S),有Se⊆eS，根据引理3.1，Reg(S)是右C半群，根据引理1.5(1)，DReg(S)=RReg(S)。设a,b∈Reg(S)且aDb，则∃c∈Reg(S)，使得aLcRb，故aDReg(S)b，即DReg(S)=D|Reg(S)。根据第二章命题4.5[11]得，RReg(S)=R|Reg(S)，故D|Reg(S)=R|Reg(S).由大前提D(+)|Reg(S)=D|Reg(S)知：D(+)|Reg(S)=R|Reg(S)。只需再证明，R(◇)=D(+)。aD(+)b⟹a+D(+)b+且a+Rb+，故aR(◇)b。

即R(◇)⊇D(+)，显然有R(◇)⊆D(+)。

推论2.3设S是一个强qrpp半群且D(+)|Reg(S)=D|Reg(S)，则S是右C-qrpp半群当且仅当

R(◇)是S上的半格同余且Reg(S)是右C半群。

证明(⟹)设S是右C-qrpp半群，根据定理2.2得，R(◇)是S上的半格同余且∀e∈E(S),有Se⊆eS，由引理2.1得，Reg(S)是右C半群。

(⟸)在定理2.2的⟸证明中已证。

引理2.4[13]在带B中，B是右正则的当且仅当B右零带的半格。

定理2.5设S是一个强qrpp半群且D(+)|Reg(S)=D|Reg(S)，∀e∈E(S),有Se⊆eS，则下列条件等价：(1)S是右C-qrpp半群，

(2)R(◇)=J(+)，

(3)D(+)=J(+)。

证明：(1⟹2)设S是右C-qrpp半群，根据定理2.2，则R(◇)是S上的半格同余。可设S=∪α∈YSα，其中Y是半格，Sα是S的一个R(◇)类。令a∈Sα,b∈Sβ，则J(+)(a)=∪x∈J(+)(a)Jx(+).而R(◇)⊆D(+)⊆J(+)，有J(+)(a)=∪γ∈Y,γ≤αSγ，J(+)(b)=∪γ∈Y,γ≤βSγ故J(+)(a)=J(+)(b)当且仅当α=β。因此，aJ(+)b⟺J(+)(a)=J(+)(b)⟺α=β且R(◇)=J(+)。

(2⟹3)由R(◇)⊆D(+)⊆J(+)且R(◇)=J(+)可知D(+)=J(+)。

(3⟹1)设D(+)=J(+).∀e∈E(S),有Se⊆eS，根据引理2.1可知，Reg(S)是右C半群，根据引理1.5(1)得，DReg(S)=RReg(S)，进而D(+)|Reg(S)=R|Reg(S).还需证明，R(◇)是S上的半格同余。分两步来证明：第一步，证明J(+)是S上的半格同余。L(+)是S上的右同余，a∈S，有a2L(+)a+a,a2J(+)(a).于是J(+)(a2)=J(+)(a)。设u,v∈S，则J(+)(uv)=J(+)((uv)2)=J(+)(u(vu)v)⊆J(+)(vu)，同理J(+)(vu)⊆J(+)(uv)，故J(+)(vu)=J(+)(uv)。设a,b,u∈SauL(+)a+uJ(+)ua+L(+)u+a+,buL(+)b+uJ(+)ub+L(+)u+b+,即auJ(+)u+a+，buJ(+)u+b+。设aJ(+)b,则a+Rb+，由引理2.4得u+a+Ru+b+，根据J(+)的定义得auJ(+)bu。

故J(+)是S上的半格同余。第二步，aJ(+)b⟹aD(+)b⟹a+D(+)b+⟹a+Rb+,于是aR(◇)b，即J(+)⊆R(◇)从而J(+)=R(◇).综合第一步和第二步得R(◇)是S上的半格同余。

设B=∪α∈YEα是带B的矩形带半格分解，若e∈Eα，为了方便，E(e)表示Eα，Eα≤Eβ表示EαEβ⊆Eα.

引理2.6[8]半群S是C-wrpp半群当且仅当S是左R可消幺半群的强半格。(Theorem3.1[8])。

定理2.7设S是强qrpp半群，其幂等元集E(S)是个带，则S是右C-qrpp半群当且仅当ζ={(x,y)∈S×S|(∃f∈E(y+))x=yf}是S上的C-wrpp半群同余。

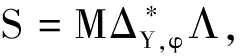
(u,i)ζS(v,j)⟹∃(k∈Λβ)(u,i)=(v,j)(1β,k)⟹u=v且α=β。反过来，若u=v且α=β,则(u,i)=(v,j)(1α,i)⟹(u,i)ζ(v,j)。这就是说，(u,i)ζ(v,j)当且仅当u=v且α=β。

根据同余和同构的定义有：ζ={(x,y)∈S×S|(∃f∈E(y+))x=yf}是S上的同余且S/ζ≅M。ζ是S上的C-wrpp半群同余。

(⟸)设ζ={(x,y)∈S×S|(∃f∈E(y+))x=yf}是S上的C-wrpp半群同余。若aζ是幂等元，即(a2,a)∈ζ，则∃f∈E(a+)使得a2=af，于是a2=a2a+=afa+=aa+fa+=aa+=a∈E(S)。也就是说，ζ是幂等元纯的。可以断言，ζ|E(S)=R|E(S)。实际上，ζ⊆R(y=yy+=yy+fy+=yfy+=xy+)。设e,f∈E(S)且eRf，则E(e)=E(f)，e=fe,即eζf。故ζ|E(S)=R|E(S)。

下面证明ζ是保持L(+)类的。∀x,y∈S1，若(aζ·xζ,aζ·yζ)∈R，则((ax)ζ,(ay)ζ)∈R，即∃u,v∈S1，使得(axu)ζ=(ay)ζ,(ayv)ζ=(ax)ζ。由ζ⊆R得，(axu,ay)∈R,(ax,ayv)∈R。设(a,b)∈L(+)，则(bxu,by)∈R,(bx,byv)∈R。∃s,t∈S1使得bxus=by,bx=byvt，则(bxus)ζ=(by)ζ,(bx)ζ=(byvt)ζ，即((bx)ζ,(by)ζ)∈R.这就是说(a,b)∈L(+)，则∀x,y∈S1,(aζ·xζ,aζ·yζ)∈R⟹(bζ·xζ,bζ·yζ)∈R，反过来(bζ·xζ,bζ·yζ)∈R⟹(aζ·xζ,aζ·yζ)∈R,即(aζ,bζ)∈L(+).

以下记E(S)为E，概括起来已经证得，E/(ζ|E)=E(S)/(R|E)=E(S/ζ)是个半格，即E是右零带的半格，根据引理2.4，E右正则带。可设E=∪α∈YΛα，其中Y是半格，Λα是右零带。可看做Y=E(S/ζ)。根据引理2.6，S/ζ=∪α∈YMα，其中Y是半格，Λα是左R可消幺半群。记T=∪α∈Y(Mα×Λα)，可以定义映射θ:S→T,θs=(sζ,s+)，设(m,λ)∈T，则∃s∈S，使得sζ=m,s+Rλ，s+ζ=λζ.故(sλ)ζ=sζ·λζ=sζ·s+ζ=(ss+)ζ=sζ=m.又sλL(+)s+λ=λ,sλλ=sλ=s+sλ=λs+sλ=λsλ得，(sλ)+=λ。因而(sλ)θ=(m,λ)且θ是满射。对于θ，有sθ=tθ⟹sζt且s+=t+，又sζt⟹(∃e∈E(t+))s=te，于是s=ss+=tet+=tt+et+=tt+=t，故θ是双射。

在T上定义⊗：(sζ,s+)⊗(tζ,t+)=((st)ζ,(st)+)，易见运算满足结合律，故(T,⊗)是半群且θ是同构映射。另一方面，(sζ,s+),(tζ,t+)∈Mα×Λα⟹t+s+=s+,s+t+=t+，故stL(+)s+t=(s+t+)t=t+t=tL(+)t+.由stt+t=st=s+st=t+s+st=t+st得，(st)+=t+，(st)+=s+t+，这就表明T是Mα×Λα的半格，根据引理1.2得S是右C-qrpp半群。

3 右C-qrpp半群的半织积结构

半织积的概念由文[1]提出来，受其启发，下面给出右C-qrpp半群对偶半织积结构。

定义3.1设T=∪α∈YTα，Λ=∪α∈YΛα分别是半群T和Λ在半格Y上的分解。构造Cartesian积Sα=Tα×Λα，令S=∪α∈YSα，建立映射η:S→Tr(Λ),(a,λ)|→η(a,λ),μη(a,λ)=μ(a,λ),其中Tr(Λ)是半群Λ上的右平移变换构成的半群，设(a,λ)∈Sα,(b,μ)∈Sβ,要求η满足：

(C1)μ(a,λ)∈Λαβ;(C2)当α≤β时，μ(a,λ)=μλ;(C3)η(a,λ)η(b,μ)=η(ab,λ(b,μ)),

引理3.2[7]设Y是半格，S=[Y;Sα,θα,β]是Sα的强半格，则R(Sα)=R(S)∩(Sα×Sα)。

(1)E(S)=∪α∈Y({1α}×Λα);

(2)∀(a,λ)∈Tα×Λα,(a,λ)L(+)(1α,λ)；

(3)S是右C-qrpp半群且∀(a,λ)∈Tα×Λα,(a,λ)(+)=(1α,λ).

证明(1)若(a,λ)2=(a,λ)，则∃α∈Y使得(a,λ)∈Sα且a2=a∈Tα.注意到Tα是左R可消幺半群，则a=1α.反过来，(1α,λα)2=(1α1α,λα(1α,λα))=(1α,λαλα)=(1α,λα)。故E(S)=∪α∈Y({1α}×Λα)。

(2)设(x,j),(y,k)∈S1，(a,λ)(x,j)R(a,λ)(y,k)，则axRay⟹(∃γ∈Y)ax,ay∈Tγ。

由引理3.2得axR(Tγ)ay，又Tγ是左R可消幺半群，故1αxR(Tγ)1αy.计算(1α,λ)(x,j)=(1αx,uγ)，(1α,λ)(y,k)=(1αy,vγ)，由Λγ是右零带可知，(1α,λ)(x,j)R(1α,λ)(y,k)。

反过来，若(1α,λ)(x,j)R(1α,λ)(y,k)，由R是左同余知(a,λ)(x,j)R(a,λ)(y,k)。

故∀(a,λ)∈Tα×Λα,(a,λ)L(+)(1α,λ)。

定理3.4设S是半群，则S是右C-qrpp半群当且仅当S同构于一个C-wrpp半群和一个右正则带的对偶半织积。

证明(⟸)根据引理2.6和定理3.3得证；

(⟹)设S是右C-qrpp半群。根据引理2.1和引理1.5(2)，幂等元集E是右正则带。设E=∪α∈YEα是E的右零带Eα半格分解，根据定理2.7，Y≅E(S/ζ)，不妨假设Y=E(S/ζ)。根据引理2.6，设S/ζ=∪α∈YMα是C-wrpp半群S/ζ的左R可消幺半群Mα的强半格分解，其中的每个Mα都是S/ζ的一个L(+)类[8]，记M=S/ζ，T=∪α∈Y(Mα×Eα)，由定理2.7的证明可知，映射θ:S→T,θs=(sζ,s+)是双射，T关于⊗：(sζ,s+)⊗(tζ,t+)=((st)ζ,(st)+)是半群且S≅T。

可以建立映射τ:T→Γr(E)，(sζ,s+)|→τ(sζ,s+);其中iτ(sζ,s+)=i(sζ,s+)=(is)+,Γr(E)是E的右平移变换半群。由于L(+)是右同余，于是s1s2L(+)s1+s2，根据命题1.3得，(s1s2)+R(s1+s2)+，因而，(s1+s2)+(s1s2)=(s1+s2)+(s1s2)+(s1s2)=(s1s2)+(s1s2)=s1s2=s1s1+s2=s1(s1+s2)(s1+s2)+=(s1s2)(s1+s2)+，即(s1s2)+=(s1+s2)+。

计算得，(s1ζ,s1+)⊗(s2ζ,s2+)=((s1s2)ζ,(s1s2)+)=((s1s2)ζ,(s1+)(s2ζ,s2+))，这满足定义3.1(C1)；设(aζ,a+)∈Mα×Eα,e∈Eβ,α≤β，计算得，

(eζ,e)⊗(aζ,a+)=(eζ,e)⊗(a+ζ,a+)⊗(aζ,a+)=((ea+)ζ,ea+)⊗(aζ,a+)=((ea)ζ,ea+)=((ea)ζ,e(aζ,a+))

这满足定义3.1(C2)；设(bζ,b+)∈Mβ×Eβ,f∈Eγ，计算得，

(eζ,e)⊗(aζ,a+)⊗(bζ,b+)=(eζ,e)⊗((ab)ζ,(a+)(bζ,b+))=((eab)ζ,eτ((ab)ζ,(a+)(bζ,b+)))

且

(eζ,e)⊗(aζ,a+)⊗(bζ,b+)=((ea)ζ,e(aζ,a+))⊗(bζ,b+)

=((eab)ζ,eτ(aζ,a+)τ(bζ,b+))

于是，τ((ab)ζ,(a+)(bζ,b+))=τ(aζ,a+)τ(bζ,b+)，这满足定义3.1(C3)；