MATLAB 在污水管道水力计算中的应用研究

2022-07-04陈嘉禾

科技创新与应用 2022年19期

陈嘉禾

（湖南大学土木工程学院，湖南长沙 410082）

设计污水管道就必须对污水管道进行水力计算，对此传统的方法是根据各水力参数的限制范围，在水力计算图中查出一组可行的设计方案。这实际上是一项十分繁琐的工作，并且精度不高，不利于设计方案的优化。笔者在本文中将介绍一种新的方法——用MATLAB 来编程。

MATLAB 是目前常用的工程软件，它集数值计算、矩阵计算和图形绘制等功能于一体，广泛应用于各种数学及工程计算中。它采用数学语言编写程序，更加通俗易懂，并且自带矩阵和数组的运算函数，减少了编程和调试的工作量，这就是MATLAB 相比于其他语言如Fortran、C++等的显著优点。

截至目前，已经有不少学者成功应用MATLAB 解决了一些工程计算问题，如进行梯形明渠、供热管网、燃气管网的水力计算；建立供水管网平差模型等。大大缩短了计算时间，提高了计算精度和工作效率。

1 污水管道水力计算的试算法及程序框图

1.1 污水管道水力计算的试算法

对于无压圆管流，其水力计算基本公式有：

对以上公式进行整理可知，h/D和R均为θ 的函数，而v、I和θ 均同时为θ 和v的函数。因此，可先假定设计流速v的值，再算出其他参数的值。

此外，还应考虑到在污水管道水力计算过程中可能涉及到的约束条件：

a. 管径D对应的最小流量Q（min）；

b. 管径D对应的最大充满度h/D（max）；

c. 管径D对应的最大流速v（max）；

d. 管径D对应的最小水力坡度I（min）；

e. 管径D对应的最大水力坡度I（max）。

结合上述分析及约束条件，可整理得出污水管道水力计算的试算法，步骤如下：

（1）绘出计算草图，对各点、管段进行编号；

（2）计算各管段设计流量；

（3）根据约束条件a 和设计流量，求出各管段对应的最大管径；

（4）对每段管段的每种可能管径，使设计流速v从最小值（0.6 m/s）以步长（0.01 m/s）增大到相应的最大值（约束条件c），计算相应的θ、R、h/D、I；

（5）判断求出的h/D和I是否同时满足约束条件b、d、e；

（6）若满足，则记录这一组设计方案；若不满足，则继续试算下一个设计流速v，直至计算出所有管段的所有可行方案为止。

1.2 程序框图

试算法计算程序框图如图1 所示。

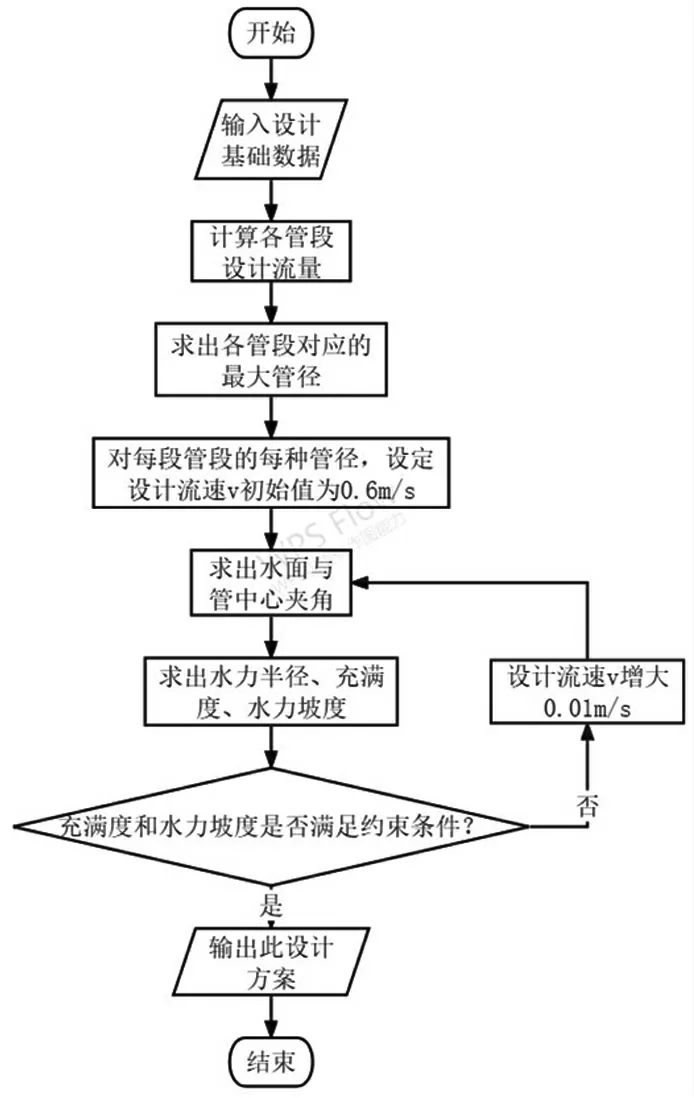
图1 试算法计算程序框图

2 计算实例

2.1 例题

【例】用试算法计算排水管道，如图2 所示。设节点流量Q1=24.28，Q2=12.4，Q3=14.6，Q4=9.5，Q5=8.7，Q6=12.8，单位均为L/s。

图2 具有6个排出口的污水管道示意图

2.2 示例程序

用MATLAB 编写如下程序就能对这一管道进行水力计算。

%水力约束矩阵,按列依次为D-Q(min)对应关系,D-(h/D)(max)对应关系,D-v(max)对应关系,D-I(min)对应关系,D-I(max)对应关系

%标准管径向量

注:在实际应用中,技术人员应根据工程实际情况适当改变水力约束矩阵中的数值。(如街坊管道的最小管径为200 mm,市政管道的最小管径为300 mm;坡度阈值可参考实际地形坡度设定等)

2.3 计算结果

由于计算结果数目较大, 此处只列出第一段管段第一种管径(200 mm)的计算结果:

设计流量计算结果(L/s):

管径流速充满度水力坡度

第1 段管段：当管径为200 mm 时共有118 种设计方案。

3 分析讨论

3.1 与手工查表的比较

手工查表需要先在不同管径对应的水力计算表中找到流量所对应的列，然后在考虑多种约束条件的情况下选择一组合适的水力参数值。这一过程步骤繁琐、用时较长，加之水力计算表的数据密集性较高，给技术人员准确查找数据带来了不小的困扰。此外，第一次查出的数据可能无法满足后期设计埋深的要求，导致技术人员需要重新查找，这也将耗费大量时间。总体来说，这种方法过程繁琐、效率较低。

在笔者的计算机上运行整个程序，总用时为749 s（在不同的计算机上运行结果不同，用时与计算机的速度有关），这比手工查表节省了许多时间。因此，与手工查表相比应用MATLAB 进行污水管道水力计算，速度快，效率高。