轻量化火星遥感影像超分辨率重建网络

耿铭昆，吴凡路，王 栋

（1. 中国科学院长春光学精密机械与物理研究所，吉林 长春 130033；2. 中国科学院大学，北京 100049；3. 中国科学院月球与深空探测重点实验室，北京 100101）

1 引 言

高分辨率火星遥感影像对人类全面了解火星的地貌地表状态、太阳系起源与演化、火星着陆区的精细勘测和火星车的路径规划起到了至关重要的作用。但由于深空探测的运载能力远不能与地球轨道的大吨位运载能力相媲美，有效载荷的重量依然是执行深空探测任务的首要考虑因素。受限于重量约束，行星遥感相机口径、焦距一般配置不高，分辨率往往不能满足更精细、更微观的使用需求。因此在较低的硬件配置条件下通过软件算法对火星遥感影像进行超分辨率重建成为重要研究方向。

图像超分辨率重建技术旨在通过软件方法从相应的低分辨率图像中恢复具有丰富高频细节的高分辨率图像，1964 年，Harris［1］首次提出“图像超分辨率”这一概念。1984 年，Tsai 等人［2］利用多张低分辨率图像通过傅里叶变换域处理获得了一张高分辨率图像，这是利用软件技术进行图像超分辨率重建的首次尝试。此后又先后出现了插值法、重构法［3-4］、基于例子［5］的方法和基于浅层学习［6-7］的方法等软件方法。目前，图像超分辨率重建在医学成像［8］、安防监控［9］和遥感成像［10-11］等诸多领域均有大量应用。

近年来，基于卷积神经网络的算法在计算机视觉领域展现了突出的性能［12-13］，而在图像超分辨率领域基于卷积神经网络的方法也以其高性能和快速的预测速度成为主流方法。但由于参数量大、计算量大，大多数方法都不能很好地适应遥感影像。因此，用轻量化网络得到良好的火星遥感影像超分辨率效果是一项具有挑战性和关键性的任务。

2016 年，Dong 等人［14］首次提出了一种由三层卷积层组成的神经网络模型，称为SRCNN。然后，Kim 等人［15］在DRCN 中通过使用跳跃连接和递归监督避免训练中出现梯度消失、梯度爆炸现象，该网络通过使用参数共享的递归层使得参数量在一定程度上降低且加快了训练，但由于使用卷积核通道数多导致参数量仍然较大。Lai 等人［16］提出的LapSRN 采用了拉普拉斯图像金字塔作为网络的主体框架，与其他网络对输入的LR 先上采样再计算不同的是该网络对残差图像的推断计算在低分辨率下进行，故节省大量运算量，但不足之处在于其参数量仍然较大。

针对上述问题，本文结合DRCN 与LapSRN的优点提出一种轻量化拉普拉斯金字塔递归残差网络（Lightweight Laplacian Pyramid Recursive and Residual Network，LRN）。本文将参数共享思想引入LapSRN，设计了三种参数共享的递归块，并在拉普拉斯金字塔级间进行参数共享。同时对网络加入同源跳跃连接，保证了浅层特征在不断被进一步加深提取的同时在不同层级间的高效流动，提高了其在残差图像推断中的参与度。对以上改进网络进行了火星遥感影像超分辨率重建测试实验，实验结果表明：在评价指标与视觉效果上，相比LapSRN，LRN 在保持火星遥感影像超分辨率重建效果的同时实现了参数量的大幅压缩。

2 图像超分辨率重建方法

2.1 图像金字塔

图像金字塔主要有向下采样的高斯金字塔［17］（Gaussian Pyramid）和向上采样的拉普拉斯金字塔［18］（Laplacian Pyramid）两种类型，如图1所示。高斯金字塔本质上为信号的多尺度表示法，亦即将同一信号或图片多次进行高斯模糊，并且向下取样，以产生一幅图像在不同尺度下的表示Gi。拉普拉斯金字塔非常类似于高斯金字塔，由一系列残差图像构成，这些残差图像记录了高斯金字塔相邻两层的信息差值Li（下采样后再上采样获得的图像与下采样前原始图像的差值）。

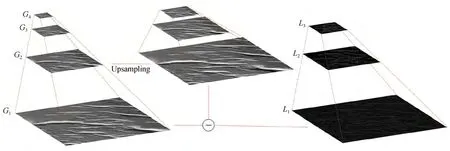
图1 图像金字塔示意图Fig.1 Schematic diagram of the image pyramid

对于大小为R×C的数字图像I，高斯金字塔的定义为：G（I）=｛G1（I），…，GN（I）｝，其中G1（I）=I是高斯金字塔的最底层即原图像，第N层为最高层即经过N-1 次下采样的图像。由第L-1 层图像GL-1（I）生成第L层图像方式如式（1）：

其中：（i，j）表示像素，0＜i≤RL，0＜j≤CL，RL为金字塔第L层图像的行数，CL为金字塔第L层图像的列数，2≤L≤N；ω为高斯低通滤波器；（m，n）为高斯核大小。

拉普拉斯金字塔的定义为：L（I）=｛L1（I），…，LN-1（I）｝。第l层图像生成方式如式（2）：

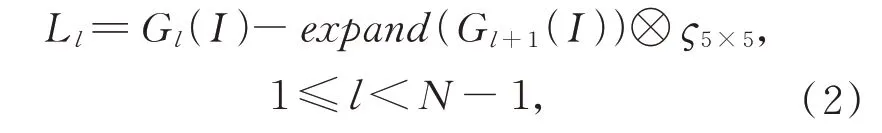
其中：expand（·）是放大算子，⊗是卷积操作，ς5×5是5×5 大小的高斯内核。

近年来，拉普拉斯金字塔结构被广泛应用于图像滤波［19］、语义分割［20］、图像融合［21］、图像生成［22］和图像超分辨率［16，23］等视觉任务。

2.2 网络结构

LRN 以拉普拉斯图像金字塔为总体框架，融合了参数共享思想、递归思想、全局与局部残差学习思想和先计算后上采样策略，其整体结构如图2所示，该网络模型由浅层特征提取子网络（Initial Feature Embedding Sub-network，IFE）、深层特征提取子网络（Deep Feature Extraction Sub-network，DFE）和图像重建子网络（Image Reconstruction Sub-network，IR）三个子网络组成。

图2 LRN 整体结构示意图Fig.2 Overall network architecture of proposed LRN model

LRN 以IFE 为起点，对LR 进行初步的特征提取如式（3），IFE 包含一个卷积层（3×3 kernels，64 feature maps，stride 1）。

其中：HIFE(·)表示对LR 应用的浅层特征提取函数，ILR表示输入网络的低分辨率图像，x1sf表示被金字塔第一级IFE 从LR 提取出来的浅层特征图。

随后x1sf作为输入传入DFE，如式（4）所示：

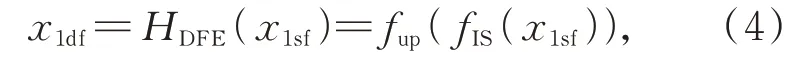
其中：x1df表示金字塔第一级DFE 输出的深层特征，HDFE(·)表示对x1sf应用的深层特征提取函数。HDFE(·)包含两个部分，第一个是fIS表示推断子网络（Inference Sub-network）函数，包含可进行参数共享的递归块（详见2.3 节），负责将输入DFE 的浅层特征进行深层次提取并推断丢失的高频信息；第二个是fup表示上采样函数，包含一个LReLU（leak=0.2）和一个转置卷积层（3×3 kernels，64 feature maps，scale=2），输出2 倍尺寸的特征图，作为输入传入IR 并得到2 倍SR 如式（5）～式（8）：

其中：I2xSR代表2 倍超分辨率图像；HIR表示图像重建函数；I2xLR表示2 倍低分辨率图像；HL1代表金字塔第一级函数；I1r代表金字塔第一级残差图像即2 倍残差图像；fres代表残差推断函数，包含一个卷积层（3×3 kernels，64 feature maps，stride 1）；ftc表示转置卷积函数，包含一个转置卷积层（3×3 kernels，64 feature maps，scale=2）。I1r由x1df经过一层残差推断卷积层得到，残差图像与低分辨率转置卷积而来的2 倍低分辨率图像逐像素相加得到2 倍超分辨率图像I2xSR。以上为金字塔第一级中2 倍超分辨率图像的生成过程。

在金字塔第二、三级，与第一级不同之处在于4 倍低分辨率I4xLR及8 倍低分辨率图像I8xLR不是直接从低分辨率图像ILR转置卷积而来，而是由2 倍和4 倍超分辨率图像I2xSR和I4xSR转置卷积而来，使包含更多高频信息的I2xSR和I4xSR在残差学习中得到利用，如式（9）、（10）所示：

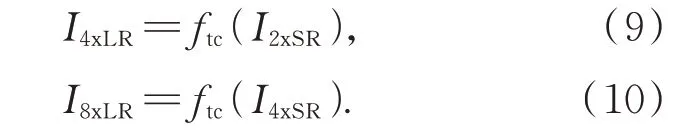
另一个不同之处在于金字塔二、三级的浅层特征x2sf和x3sf由前一级的深层特征x1df、x2df继承而来，如式（11）、（12）所示：

故4 倍超分辨率图像I4xSR及8 倍超分辨率图像I8xSR如式（13）、（14）所示：

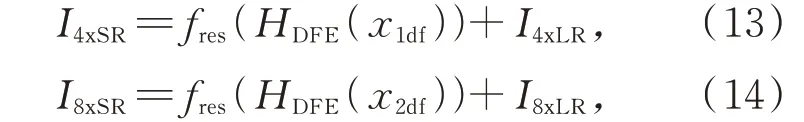
将LRN 与图像金字塔相对应可得，原高分辨率遥感影像及对其分别进行2 倍、4 倍和8 倍下采样得到的低分辨率影像对应高斯金字塔的四层，I1r、I2r和I3r对应拉普拉斯金字塔的三个层级。LRN 生成高质量超分辨率图像的关键在于残差图像的推断。残差图像应包含更多的ILR丢失的高频信息。此任务主要依赖于推断子网络输出的深层信息。

推断子网络结构如图3 所示，由r个递归块组成，并且加入同源跳跃连接，使浅层特征在层级之间流动，使其信息得到更好地保留与利用。

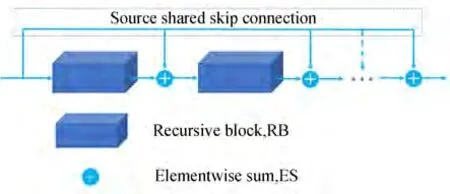
图3 推断子网络结构Fig.3 Architecture of inference sub-network

以拉普拉斯金字塔为框架的LRN 网络在一次8 倍超分辨率图像生成的前馈过程中就可以对LR 产生2 倍、4 倍以及8 倍的超分辨率结果，而不需要针对三种放大倍率准备三个不同的网络模型，故图像金字塔框架本身就是一种轻量化的框架。

2.3 轻量化设计

本文所提LRN 核心在于围绕参数共享思想进行的网络轻量化设计。LRN 在两个层面进行参数共享，一个是级间参数共享，另一个是推断子网络内参数共享。

2.3.1 级间参数共享

如图2 所示，8 倍LRN 网络包含三级金字塔结构，每一层执行一次功能类似的2 倍超分辨率任务，故可在级间进行参数共享，即每一层对应位置的卷积层、转置卷积层使用相同的权重参数。级间参数共享能将8 倍LRN 网络参数量降为约原来的1/3。

2.3.2 推断子网络内参数共享

推断子网络负责从浅层特征中提取出更深层次的特征图以进行残差推断，是LRN 网络的核心结构，本文所提LRN 由可以进行参数共享的递归块结构组成，设计了如下所述的三种不同的递归块。

2.3.2.1 块内共享递归块(Share in Recursive Block, SIRB)

SIRB 结构如图4 所示，由d层递归卷积层堆叠而成，每个卷积层前都有一个LReLU 层，每个递归块内d个卷积层共用相同的权重参数，而递归块间的参数相互独立。使用SIRB 作为递归块的LRN 称为SILRN，本文实验中提到的SILRN每一级的推理子网络均由5 个含有5 层递归层的递归块组成。

图4 SIRB 结构Fig.4 Architecture of SIRB

2.3.2.2 全共享递归块(All Shared Recursive Block, ASRB)

ASRB 与SIRB 结构相同，不同之处在于递归块间也进行参数共享。使用ASRB 作为递归块的LRN 称为ASLRN，本文实验中提到的ASLRN 每一级的推理子网络均由5 个含有8 层递归层的递归块组成。

2.3.2.3 深度递归块(Deep Recursive Block,DRB)

DRB 结构如图5 所示，在堆叠d层递归卷积层后，将每一层的输出进行级联，对级联形成的特征图阵的每一个通道乘以自适应权重ωi，再合并得到子网络输出。使用DRB 作为递归块的LRN 称为DLRN，本文实验中提到的DLRN 每一级的推理子网络均由1 个含有6 层递归层的递归块组成。

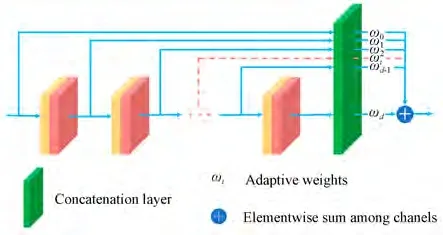
图5 DRB 结构示意图Fig.5 Architecture of DRB

2.4 损失函数

LRN 使用Lai 等人［16］提出的Charbonnier 损失函数作为损失函数，如式（15）：

3 实验与结果分析

3.1 软硬件平台

本文实验在CPU 为i7-8750H@2.20 GHz，GPU 为8 GB 显存的NVIDIA RTX2070 的计算机上进行。实验平台搭载的操作系统为Win10、深度学习框架Matconvnet1.0、CUDA10.0。

3.2 数据集与评价指标

本文选择了高分辨率成像科学实验相机［24］（High Resolution Imaging Science Experiment，HIRISE）拍摄的火星遥感影像作为数据集，其分辨率为25～50 cm/pixel，实验将编号ESP_066115_2055 的遥感影像切割成3 795 张512×512 的图像块作为训练集，并对编号为ESP_066194_2100 和ESP_066828_2050 的遥感影像进行相同操作，并从中选择20 张作为验证集、60 张包含平原、丘陵、山脉和陨石坑等多样地貌特征的火星遥感影像作为测试集，部分影像如图6 所示。训练集、验证集以及测试集三个数据集无重复影像。

图6 火星遥感影像测试数据集示例图像Fig.6 Sample images of Mars remote sensing image test dataset

本文使用峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）、结构相似性（Structural SIMilarity，SSIM）以及信息保真度准则（Information Fidelity Criterion，IFC）作为重建图像质量的客观评价指标。

3.3 数据准备

为了增强网络的泛化性，在训练时使用数据增强来扩充训练集，主要包括三种方式：（1）下采样：对所有训练集图片进行随机下采样，采样因子范围为［0.5，1.0］；（2）旋转：对所有训练集图片随机旋转90°、180°、270°；（3）水平翻转：以0.5的概率水平翻转所有训练集图片。本文通过双三次插值算法对训练集进行下采样，从而产生低分辨率输入图像，原图作为真实高分辨率图像。

3.4 网络参数与训练策略

在所提出的LRN 中，每个卷积层有64 个大小为3×3 的卷积核。本文使用He 等人［25］的方法对卷积核进行初始化。反卷积核的大小为4×4，权值由双线性滤波器初始化。所有卷积和转置卷积层（除重建层外）后面是负斜率为0.2 的泄漏整流线性单元（LReLU）。在应用卷积之前，在边界周围填充零，保持所有特征图的大小与每个级别的输入相同以便于相加。

网络训练策略方面，本文提出的LRN 使用随机梯度下降（Stochastic Gradient Descent，SGD）的策略来优化网络，其中SGD 动量参数设置为0.9，权重衰减为10-4。对于所有层，学习速率被初始化为10-5，并且每50 个Epoches 将学习速率乘以0.8。由于GPU 显存的限制，本文将训练数据集裁剪成128×128 的图像块作为训练对象。

3.5 实验结果对比分析

表1 给出了ASLRN 在8 倍下对60 张火星遥感测试影像进行超分辨率测试时PSNR、SSIM以及IFC 三个客观评价指标的具体数值。表2 给出了SILRN、ASLRN、DLRN、LapSRN、Bicubic等方法在2 倍、4 倍和8 倍三种不同放大倍数下对测试集中60 张火星遥感影像进行超分辨率重建时客观评价指标的平均值及相应参数量。实验中使用的LapSRN 网络已按照原作者给出的训练参数使用与其他三种网络相同的火星遥感影像数据集进行重新训练以保证测试结果的公平性。

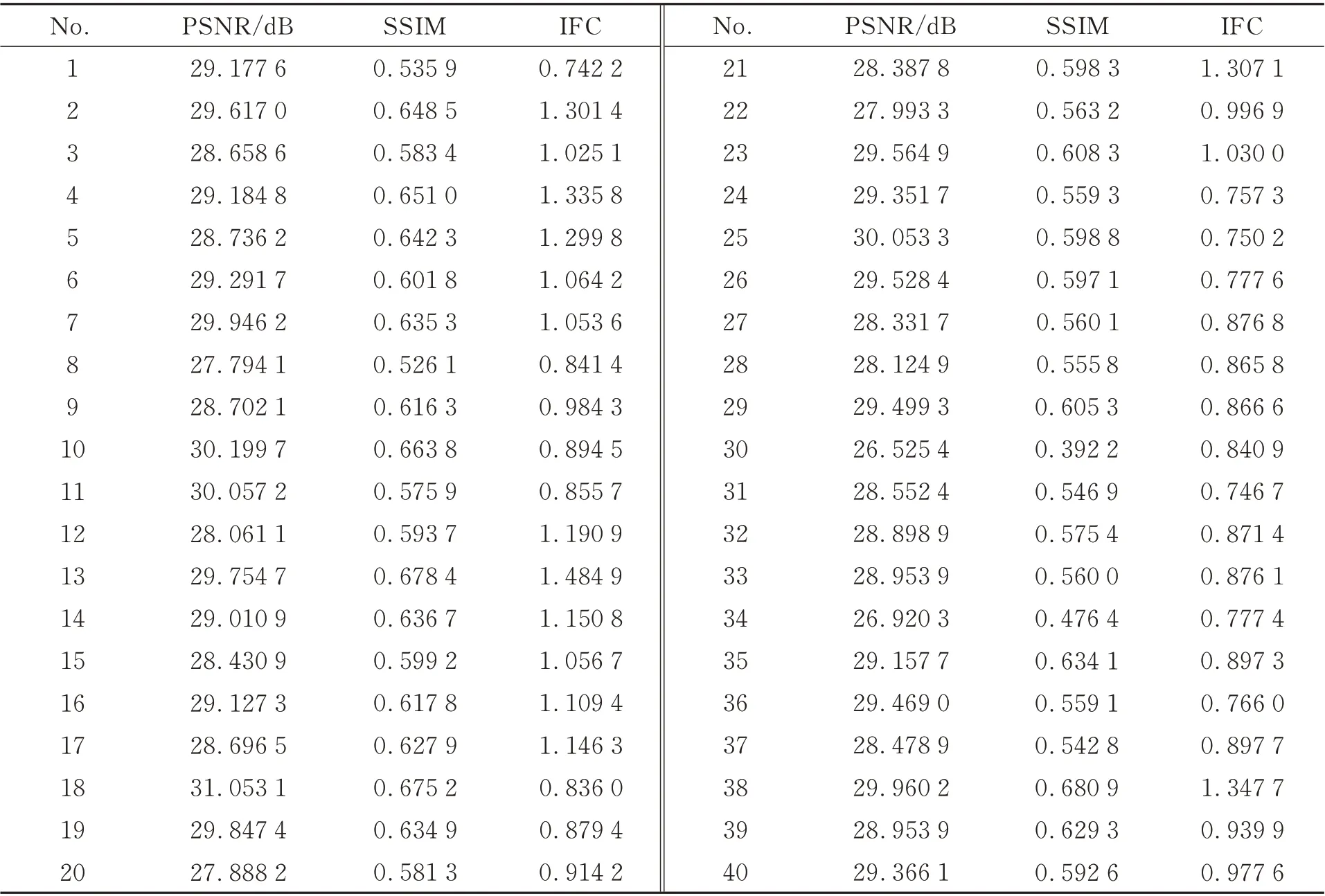
表1 ASLRN 对火星遥感影像测试数据集8 倍超分辨率重建的客观评价指标具体值Tab.1 Objective evaluation index values for×8 super-resolution on Mars remote sensing image test dataset of ASLRN

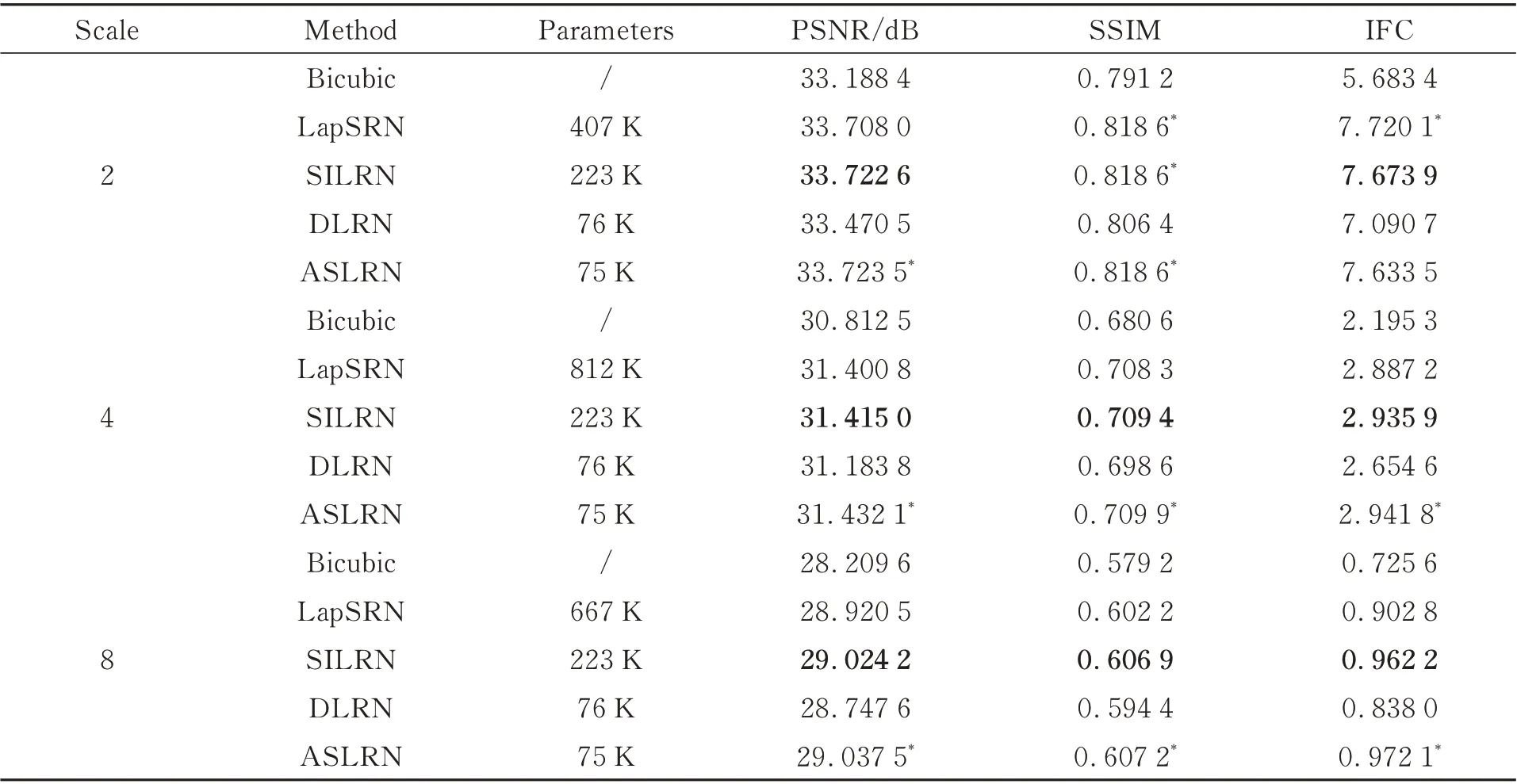
表2 火星遥感影像测试数据集上几种算法比较Tab.2 Comparison of various algorithms on Mars remote sensing image test dataset

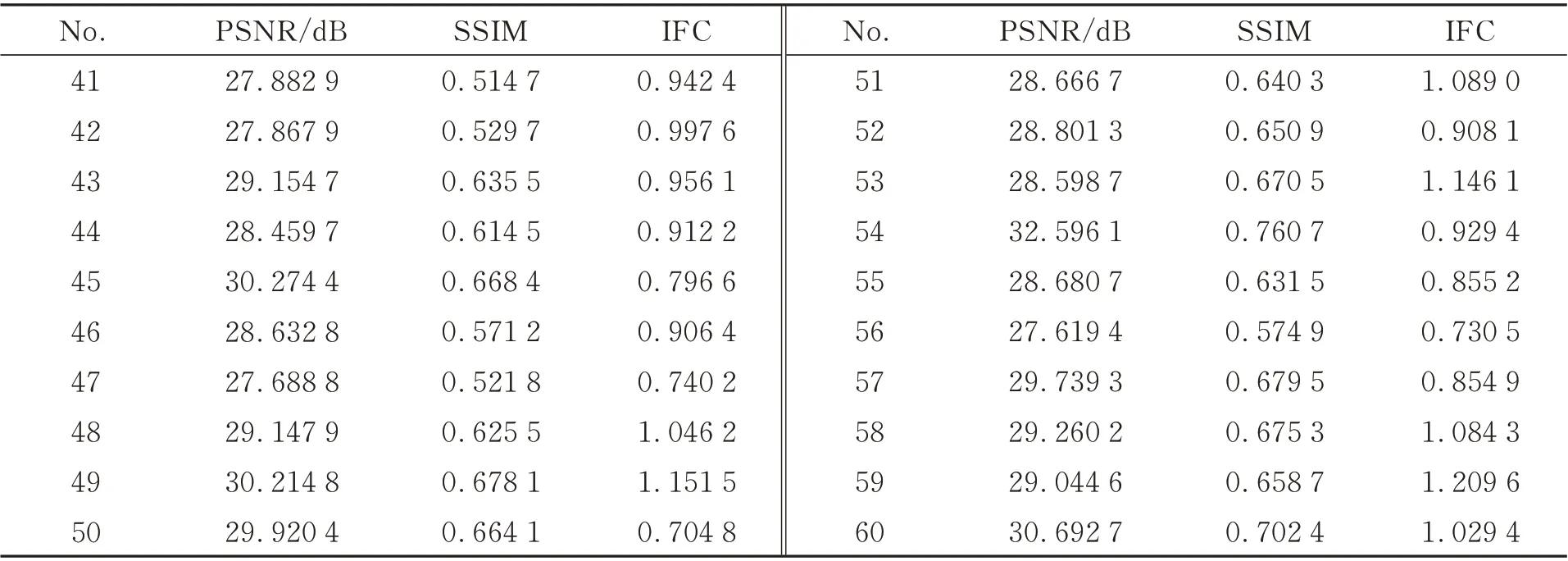
续表1 ASLRN 对火星遥感影像测试数据集8 倍超分辨率重建的客观评价指标具体值Tab.1 Objective evaluation index values for×8 super-resolution on Mars remote sensing image test dataset of ASLRN

从表1 和表2 中可以看出本文所提的三种算法中ASLRN 和SILRN 以低于LapSRN 的参数量在4 倍和8 倍超分下获得了更高的客观评价指标值。ASLRN 以低于LapSRN 一个数量级的参数量，在4 倍和8 倍超分下PSNR 分别提高了0.031 3 dB 和0.116 7 dB，SSIM 分别提高了0.001 6 和0.005 0，IFC 分别提高了0.054 6 和0.069 3。在2 倍超分下ASLRN 与LapSRN 相比，PSNR 提高了0.015 5 dB，SSIM 相同，IFC 差距小于0.1。可以认为三个倍率下ASLRN 与LapSRN 超分辨率结果无论是在像素水平上的灰度值差别还是视觉效果上都无明显差别。在SILRN 参数量约为ASLRN 三倍的情况下，认为ASLRN 是一个有良好超分辨率重建效果的轻量化网络模型，在参数量低于LapSRN 一个数量级的情况下得到了相似的网络性能。

总参数量方面，由于LapSRN 三种不同放大倍率的模型间不共享参数，故总参数量为1 886 K，而ASLRN 三种倍率只需一个网络模型就可以实现，故总参数量为75 K，仅为LapSRN 的3.98%。

图7～9 给出了SILRN、ASLRN、DLRN、LapSRN、Bicubic 等方法在2 倍、4 倍和8 倍三种不同放大倍数下对火星遥感影像测试集中部分影像的超分辨率重建效果及客观指标比较情况。从图中可以看出本文所提的三种算法中ASLRN和SILRN 以低于LapSRN 的参数量在不同重建倍数下得到了与LapSRN 无明显差别的超分辨率视觉效果，DLRN 重建效果略差。

图7 第54 幅火星遥感测试影像2 倍超分辨率重建结果对比Fig.7 Super-resolution results comparison of the No.54 Mars remote sensing test image for scale factor×2

图8 第59 幅火星遥感测试影像4 倍超分辨率重建结果对比Fig.8 Super-resolution results comparison of the No.59 Mars remote sensing test image for scale factor×4

图9 第26 幅火星遥感测试影像8 倍超分辨率重建结果对比Fig.9 Super-resolution results comparison of the No.26 Mars remote sensing test image for scale factor×8

4 结 论

本文提出了一种以拉普拉斯图像金字塔为框架的轻量化残差递归空间遥感图像超分辨率网络模型，以求在不降低重建效果的情况下降低网络的参数量。通过加入以参数共享为思想设计的递归块以及同源跳跃连接机制，使作为网络核心的推断子网络在不降低特征提取能力的情况下参数量大幅下降。所提ASLRN 方法在不降低重建效果的情况下，单倍模型参数量相对于LapSRN 降低了约一个数量级，总参数量缩减至LapSRN 的3.98%。