计及碳捕集和电转气的农村虚拟电厂多目标随机调度优化模型

李鹏，余晓鹏，张艺涵，周青青，田春筝，乔慧婷

(1. 国网河南省电力公司经济技术研究院,郑州市 450000;2. 国网河南省电力公司, 郑州市 450000;3. 华北电力大学经济与管理学院,北京市 100026;4. 南方电网能源发展研究院有限责任公司技术经济中心,广州市 510530)

0 引言

中国农村地区存在大量的秸秆、垃圾等能源资源,及广阔的土地面积为屋顶光伏和分散式风电提供了可用的空间资源[1]。 2021年6月,国家能源局提出开展整县(市、区)屋顶分布式光伏开发试点方案,要求农村居民屋顶总面积可安装光伏发电比例不得低于20%[2],这将极大推动农村分布式光伏的发展。但农村电力设备互联互通基础薄弱,难以直接联网,虚拟电厂(virtual power plant,VPP)通过先进通信技术和软件架构,实现地理位置分散的各种分布式能源的聚合和协调优化[3],为农村地区分布式能源利用提供了新的思路。

目前,国内外学者已对虚拟电厂开展了深入的研究,主要成果集中于系统构建、不确定性分析及运行模型3 个方面。 就系统构建来说,分布式电源、常规可控机组、储能和用户灵活性负荷是VPP 主要组件。文献[4]选择风电、光伏发电、碳捕集等单元组成虚拟电厂;文献[5]选用风电、光伏、光热及储能电池等组成虚拟电厂;文献[6]选用风电、光伏发电、燃气轮机及储能系统等构成虚拟电厂。 上述研究主要是针对城市分布式能源开展聚合优化,缺乏考虑农村垃圾发电(waste incineration power,WI)和生物质燃料发电(biomass power generation,BPG)。 同时,“30·60”双碳目标将有利于将农村地区的环境优势转化为经济优势,为农村地区推广燃气碳捕集(gas-power plant carbon capture,GPPCC) 和电转气(power to gas,P2G)提供了更广阔的空间。 由此,如何将农村屋顶光伏、分散式风电、垃圾发电及生物质燃料发电等分散式资源集成VPP,且将GPPCC 和P2G 嵌入VPP,将有利于充分发挥农村地区的资源和环境优势。

就不确定性分析而言,虚拟电厂主要是将分散式风电、分布式光伏及灵活性负荷等分布式资源进行集成,运行过程中面临多重不确定性因素,如何刻画其不确定性是进行最优化调度的关键。 一般来说,不确定性分析方法主要包括2 个路径,即模拟不确定性变量概率分布曲线[7]和建立不确定性度量方法[8]。 文献[9]应用拉丁超立方抽样法对风电和光伏发电的概率密度进行模拟;文献[10]利用分布式鲁棒方法对负荷不确定性进行分析和建模,用于开展随机优化模型的构建。 然而,对比上述2 种路径,前者受到外部环境影响,获得的概率分布曲线精度难以满足决策要求,后者数学方法往往过于复杂,难以直接实践应用。 实际上,不确定性分析主要是决策变量实际状态与预测值发生偏差,也称之为信息间歇,如何刻画这种信息间歇是不确定性分析的重要问题,由此,本文引入信息间隙决策理论(information gap decision theory,IGDT)[11],构造农村虚拟电厂随机调度优化模型。

就系统运行优化模型构建而言,如何针对不同构成单元运行约束,选择合理的优化目标是VPP 调度的关键。 已有研究更多选择经济效益最大化或成本最小化作为优化目标,如文献[12]基于Pareto 规则提出“聚合-分裂”机制,促进虚拟电厂的有序进化,形成虚拟电厂自组织聚合运行策略;文献[13]整合经济效益、社会效益、弃风成本等构成综合收益最大化目标;文献[14]以居民社区虚拟电厂为例,分析了经济效益最大化目标下不同组件的最优装机容量。上述相关文献未能涉及到虚拟电厂的环境效益,忽略了对VPP 运行碳排放量的测算,特别是,未能结合农村地区的资源条件,分析如何设置环境目标,引导农村地区将环境容量转变为经济效益。 由此,本文考虑到所提的农村虚拟电厂(GPPCC-P2G-WI-based VPP, GPW-VPP)中含有BPG 和WI,并且配置了GPPCC 和P2G,选取收益最大化和碳排放最小化作为优化目标。

综上,为促进农村分散式资源优化利用,本文将GPPCC、P2G 与常规虚拟电厂进行集成,构造农村碳捕集虚拟电厂,并利用IGDT 描述风电、光伏发电及用户负荷的不确定性,建立GPW-VPP 随机调度优化模型,最后以兰考能源革命试点为对象,验证所提模型的有效性和适用性。

1 农村碳捕集虚拟电厂结构与建模

1.1 农村碳捕集虚拟电厂结构

针对我国农村地区存在大量生物质秸秆、垃圾、屋顶光伏、分散式风电等分布式能源特性,本文提出将燃气碳捕集设备、电转气、垃圾发电与常规虚拟电厂集成为GPW-VPP。 其中,VPP 主要包括风电(wind power plant,WPP)、光伏发电(photovoltaic generators,PV)、生物质燃料发电及负荷需求响应(demand response,DR)。 负荷需求响应主要来源于电动汽车(electric vehicle,EV)、小工业负荷、农业负荷和居民生活负荷。 GPW-VPP 系统结构如图1所示。

根据图1,通过将GPPCC、P2G 和WI 与常规虚拟电厂相集成,可利用WPP、PV、BPG 和WI 来满足负荷需求,并通过调用负荷需求响应匹配WPP 和PV发电的不确定性。 同时,GPPCC 可用于捕集BPG 和WI 发电过程中的CO2,再利用P2G 将CO2转化为CH4,用于BPG 再次发电,实现电- 碳- 电循环优化,这将有利于实现碳的循环利用,达到近零碳排放的目标。

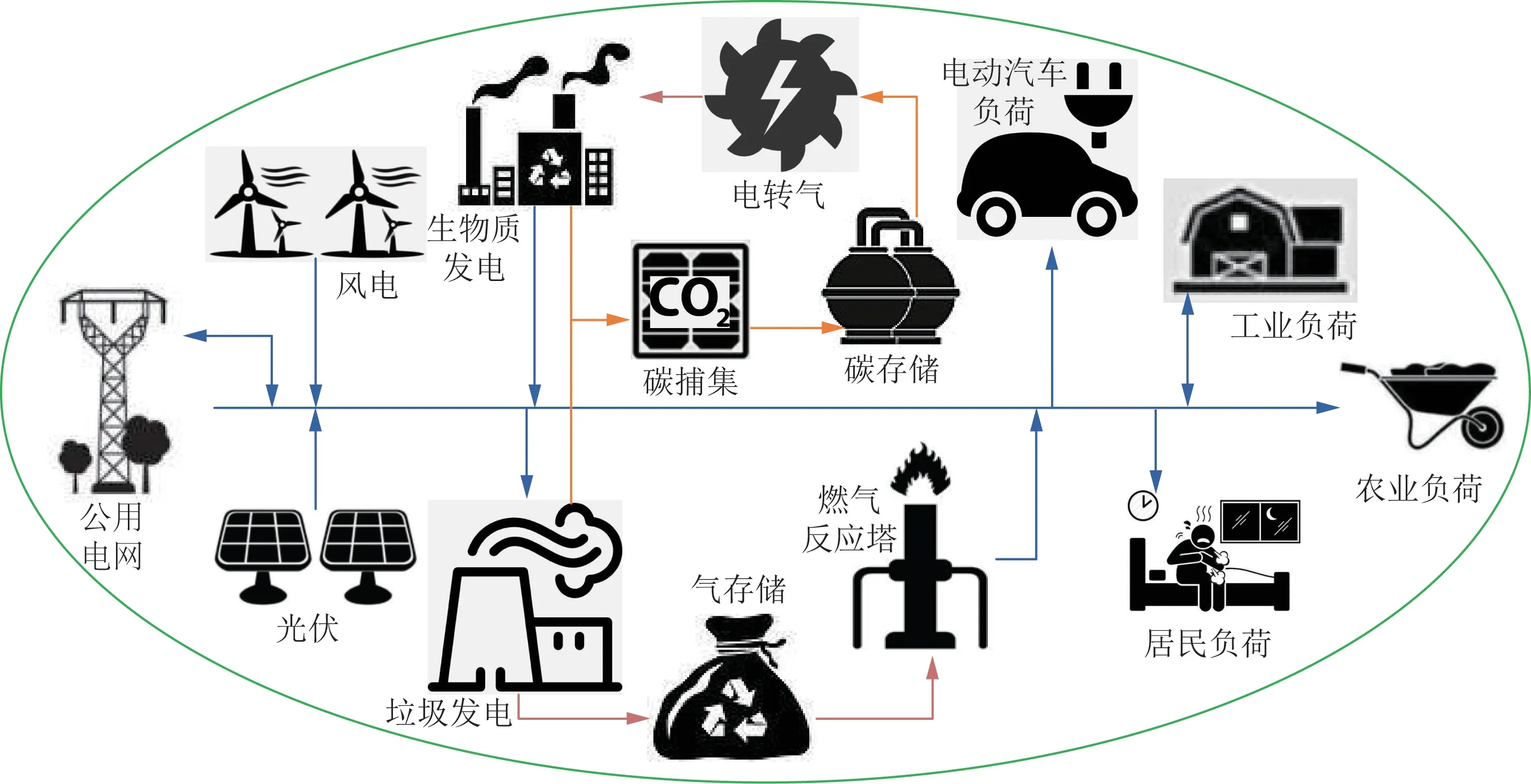
图1 GPW-VPP 系统结构Fig.1 GPW-VPP system structure

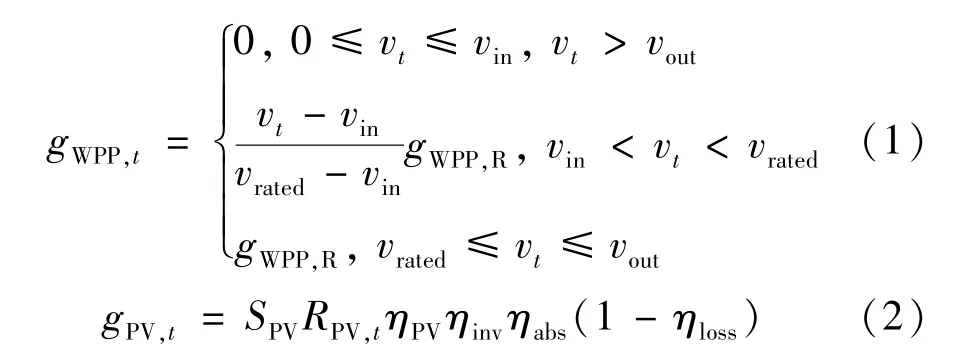
式中:gWPP,t表示WPP 在t时刻的发电出力;vt表示t时刻的自然来风风速;vin、vout分别表示切入风速、切出风速;vrated表示额定风速;gWPP,R表示WPP 的额定功率;gPV,t表示PV 在t时刻的发电出力;SPV表示PV光伏板的面积;RPV,t表示t时刻的光照强度;ηPV、ηinv、ηabs分别表示PV 的光伏模组平均效率、太阳能转换效率和太阳能吸收率;ηloss表示PV 系统损耗。

BPG 存在直燃、沼气、成型3 种方式,由于GPWVPP 存在P2G,为将P2G 产生的CH4用于发电,本文选择生物质燃料汽化发电(沼气)作为BPG 发电方式,并将CH4发电效率近似看作与沼气相同,则BPG发电出力与燃料消耗关系为[15]:

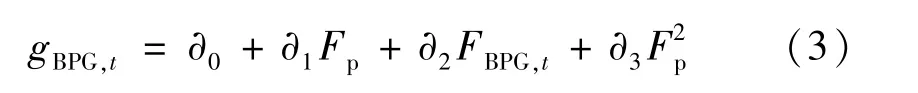
式中:gBPG,t表示沼气发电的输出功率;Fp表示沼气发电的压强;FBPG,t表示BPG 发电在t时刻的沼气消耗量;∂0为常数项系数;∂1和∂2为沼气发电压强和沼气消耗量的线性项系数;∂3为二次项系数。

垃圾焚烧发电主要通过烟气处理系统实现,由于其燃料日供应量约束,发电时间安排上具有可调节性,特别是安装烟气储气装置后,可实现发电时间与烟气处理时间的解耦,作为可控负荷参与VPP 优化调度[16]。 图2 为垃圾焚烧电厂烟气处理系统结构。

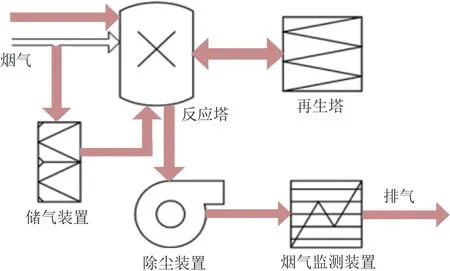
图2 垃圾焚烧电厂烟气处理系统结构Fig.2 Structure of the flue gas treatment system of a waste incineration power plant

1.2 农村碳捕集虚拟电厂建模

农村碳捕集虚拟电厂由分布式电源、灵活性负荷及GPPCC、P2G 构成。

1.2.1 分布式电源建模

WPP 和PV 发电出力主要取决于自然风速和太阳能辐射强度,尽管自然来风风速和太阳能辐射强度具有强不确定性,但已有研究证明Weibull 函数和Beta 函数可分别用于描述自然风速和太阳能辐射的分布规律,具体可见文献[3]。 WPP 和PV 的发电出力模型为:

根据图2,WI 发电产生的烟气分流进入储气装置和反应塔,引入烟气分流比λ反映流入反应塔的烟气量占总烟气量的比值,调节进入储气罐的烟气量,具体数学建模为:

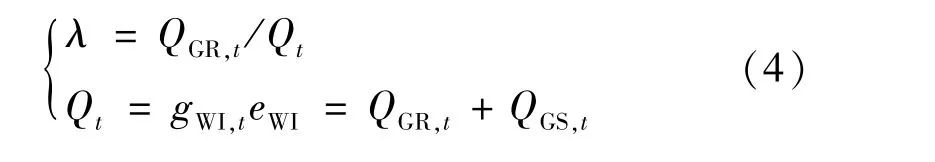
式中:Qt表示WI 在t时刻电厂产生的烟气总量;QGR,t、QGS,t分别表示t时刻进入反应塔和储气罐中的烟气量;gWI,t表示WI 在t时刻的发电出力;eWI表示WI 单位发电产生的烟气量。

WI 发电过程中还存在气泵能耗,包括储气罐进出烟气能耗和储气罐进入反应塔烟气能耗,则WI 处理烟气消耗的总功率包括气泵能耗功率和处理烟气消耗功率两部分,具体建模为:

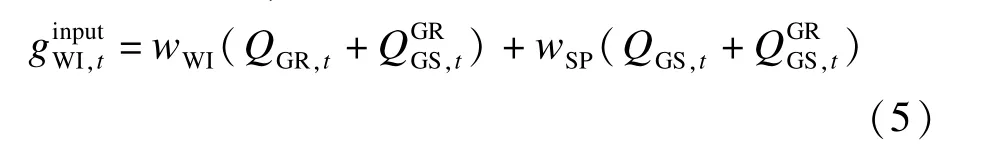
1.2.2 负荷需求响应建模

农村地区存在居民生活用电、小工业用电、电动车充电、农业用电等多种类型,且均能参与需求响应,而DR 主要包括价格型需求响应(price-based demand response,PBDR)和激励型需求响应(incentive-based demand response,IBDR)两种类型,表1 为不同类型负荷参与需求响应方式。

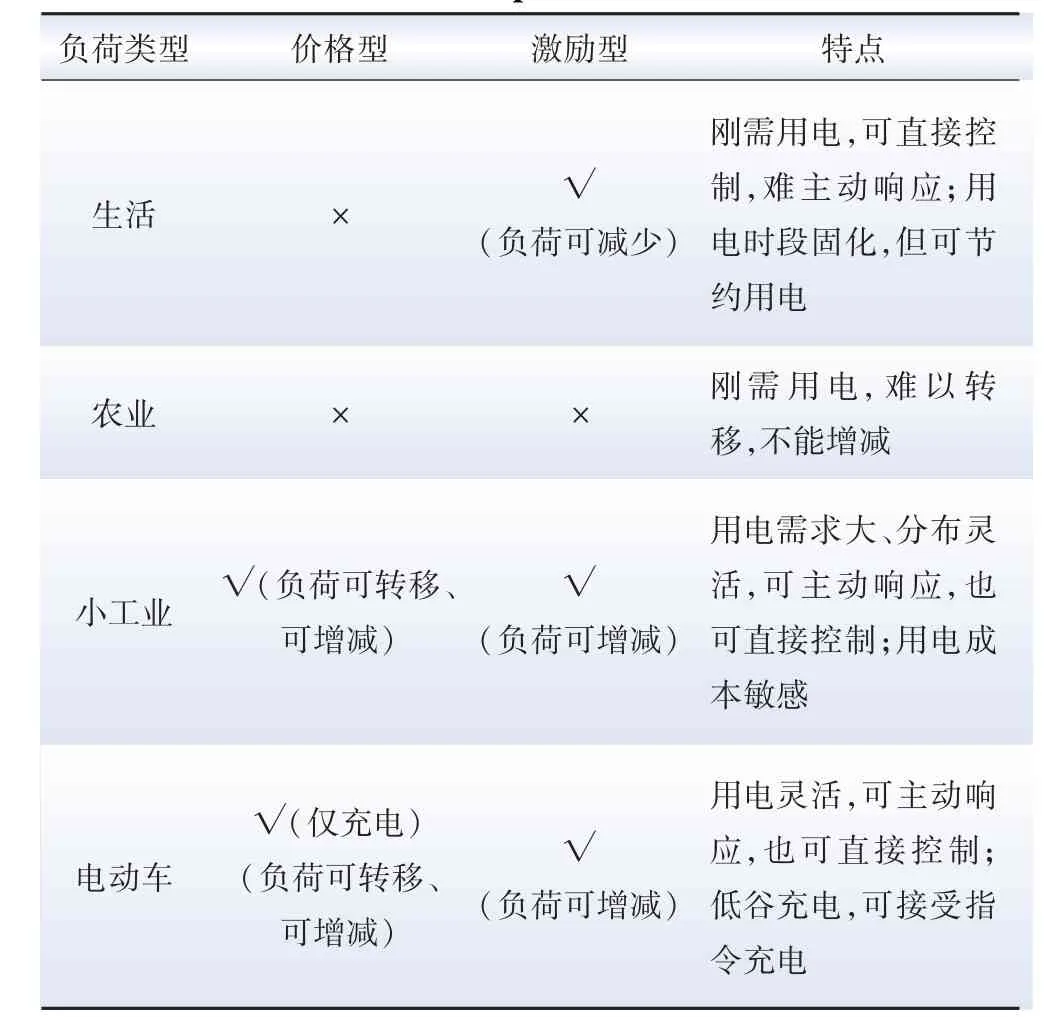
表1 不同类型负荷参与需求响应方式Table 1 Different types of loads participating in demand-response methods

根据表1,农村电动车主要是单向充电,不存在放电。 居民生活用电和农业用电是必需用电,往往难以转移,只能削减,小工业用电相对灵活,能够转移和削减,只有小工业用电负荷可提供价格型需求响应,电动车负荷可提供价格型和激励型需求响应。 因此,农村用户负荷需求响应建模为:

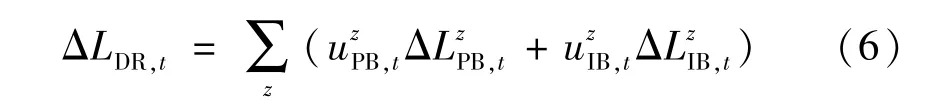
式中:ΔLDR,t表示t时刻用户提供的负荷需求响应;表示t时刻用户z是否参与PBDR 和IBDR;和表示t时刻用户z提供的PBDR 和IBDR。

PBDR 主要是利用分时电价间接引导用户调整用电负荷,是可控的负荷调节资源。

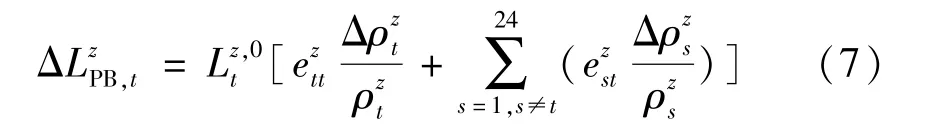
IBDR 主要是由调度中心直接控制,调用用户响应系统运行,并支付相应的备用补偿,包括合约响应负荷和紧急响应负荷。 前者通过与用户签订合约实现,后者则是当发生紧急响应需求时,根据需求情况提供不同的响应价格,用户根据紧急响应价格选择分步提供需求响应,因此,IBDR 主要包括合约响应、增加响应和减少响应三部分,具体模型为[8]:

1.2.3 GPPCC-P2G 模型

GPPCC-P2G 主要是将BPG 和WI 产生的CO2利用GPPCC 设备进行捕集,并配置储碳设备,实现碳捕集和发电时间的解耦。 GPPCC-P2G 通过捕集BPG 和WI 发电产生的CO2,用于P2G 甲烷化生成反应,直接供给WI,实现CO2循环利用,则GPPCCP2G 的能耗模型为:

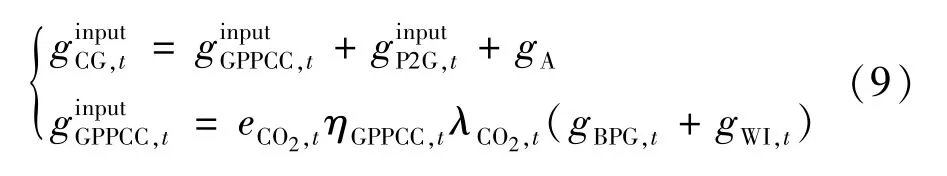
其中,与燃煤机组碳捕集有所不同,BPG 和WI产生的CO2浓度低、氧气浓度较高,故碳捕集工艺由烟气预处理、CO2吸收与溶剂再生、CO2压缩液化三部分组成,具体如图3 所示。

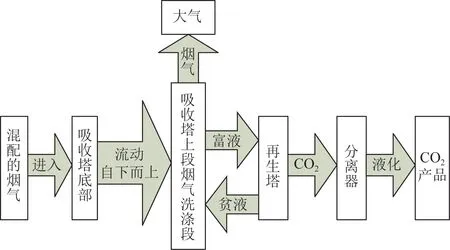
图3 GPPCC 碳捕集运行流程Fig.3 Operation process of GPPCC carbon capture

根据图3,GPPCC 主要是将BPG 和WI 产生的CO2进行捕集,进入碳储设备、P2G 和排向大气,则GPPCC 的碳捕集模型为:

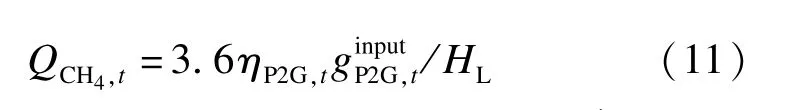
式中:QCH4,t表示P2G 在t时刻产生的CH4;表示P2G 在t时刻的耗电功率;ηP2G,t表示P2G 的设备运行效率;HL表示CH4热值。

2 农村碳捕集虚拟电厂近零碳调度优化模型

2.1 目标函数

如何将农村资源和空间优势转化为电力能源,是提高农村用户经济收益的重要方式,这使得收益最大化目标是GPW-VPP 首要优化运行的目标。 同时,由于农村具有较强的环境承载能力,更多碳配额可进入市场交易,将成为农村地区又一经济来源,故碳排放量最小化目标作为GPW-VPP 运行的第2 个目标。

1)收益最大化目标。

2)碳排放最小化目标。

GPW-VPP 的碳排放主要源于BPG 和WI,而GPPCC 和P2G 能通过捕集CO2,将其转化为CH4,若全部CO2在调度周期末存储于碳储设备中,则GPWVPP 实现了近零碳排放目标,具体目标函数为:

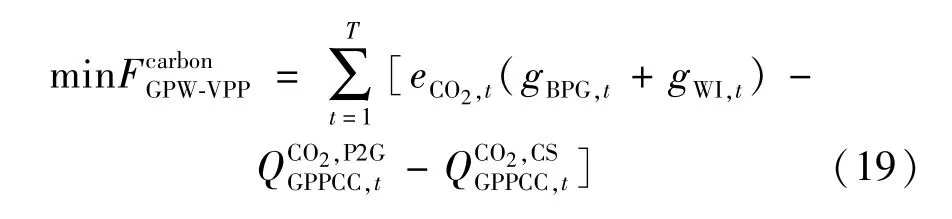
式中:表示GPW-VPP 的碳排放量;表示t时刻P2G 消耗来自GPPCC 的CO2捕集量;表示t时刻CS 再存储来自GPPCC 的CO2捕集量。

2.2 约束条件

对于GPW-VPP 来说,其运行过程中需要考虑负荷供需平衡约束、分布式电源出力约束、灵活性负荷需求响应约束及GPPCC-P2G 运行约束。

1)负荷供需平衡约束。

2)分布式电源出力约束。

VPP 中,WPP 和PV 发电出力不能超过最大发电能力[7],BPG 出力包括自身发电出力和来自P2G提供CH4的发电出力,设,则出力约束为:

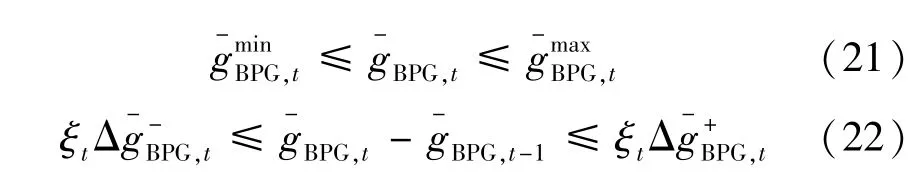
对于WI 来说,主要包括GR 和GS 两部分,涉及到GR 发电约束和GS 储气约束,这就要求满足最大运行功率约束和最大储气量约束,具体约束条件为:

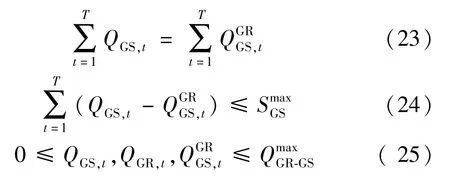
3)灵活性负荷需求响应约束。

DR 运行约束需要考虑负荷调整能力约束、最大变动量约束、负荷爬坡能力和上下调峰能力约束等。PBDR 产生的用户负荷响应及IBDR 提供的合约负荷响应均不能超过最大允许响应[7]。

4)GPPCC-P2G 运行约束。

GPPCC 须考虑最大运行功率约束和碳储设备运行约束,GS 须考虑不能超过最大允许储气容量,具体约束条件如下:

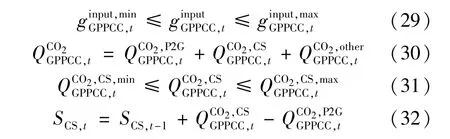
3 农村碳捕集虚拟电厂随机调度优化模型

3.1 IGDT 模型

VPP 的不确定性主要源于WPP、PV 和用户的灵活性负荷,如何刻画不确定性因素的波动特性是构建优化运行模型的重要前提。 实际上,不确定性分析主要是决策变量实际状态与预测值发生偏差,也称之为信息间隙,如何刻画这种信息间歇是不确定性分析的重要问题。

为解决这类信息间隙问题,Yakov Ben-Haim 等人在20 世纪80年代提出并不断完善了IGDT,用于描述不确定性信息已知和未知之间的间隙状态,分析不确定性程度及后果,从而制定更加符合实际的决策方案[17]。 IGDT 基本模型包括系统模型、不确定性模型和最低需求模型。 对于任一个初始系统模型,均可写成目标函数、不等式约束和等式约束的形式,具体为:

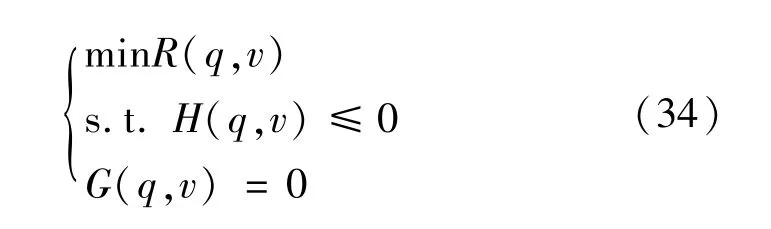
式中:R(·)为目标函数;q为确定参数;v为不确定参数;H(·)为不等式约束;G(·)为等式约束。 考虑不确定性变量v,其对应的预测值是,则可利用区间对不确定性变量的浮动状态进行描述,具体为:

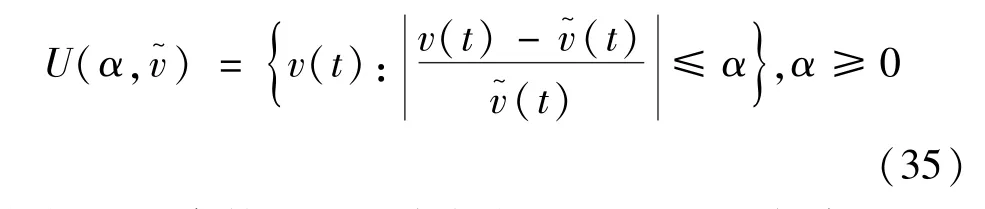
式中:α为参数v的不确定度,也就是对于集合U(α,中的v,其相对于预测值的最大扰动量为。

最低需求模型主要用于描述不确定性变量预测值偏差给系统决策带来的影响,考虑参数rc为决策者能够接受的目标值下限,则对于任意参数v,目标函数R(q,v)都能够满足如下约束[18]:

根据式(34)—(36)可将原初始系统决策模型转化为不确定性决策模型,具体为:

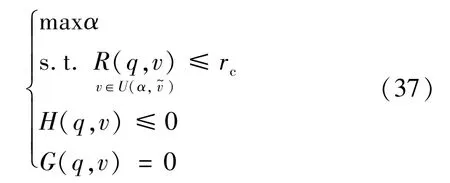
通过上述最优模型能保证在决策者能够接受的目标值前提下,承受不确定性参数的最大化波动。 通过式(37)求取决策值q,能保证v在集合内扰动时,都能取得决策者可接受的目标值rc。

3.2 随机调度优化模型

GPW-VPP 存在WPP、PV 和用户负荷3 个不确定性变量,GPW-VPP 优化决策是以不确定性变量预测信息为基础数据,当不确定性变量实际值与预测值发生偏差时,即认为发生了信息间隙。 因此,本文利用IGDT 方法构造GPW-VPP 随机调度优化模型,该方法通过分别构造与上述2 个方向对应的风险规避(鲁棒)模型和风险投机(机会)模型,形成一个开放式的决策优化策略。

首先,处理WPP、PV 和用户负荷的不确定性,具体为:

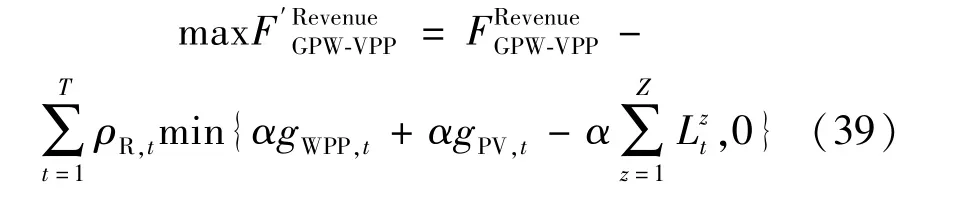
式中:ρR,t表示t时刻单位弃风成本。

传统IGDT 方法只能将单目标模型转换为不确定性决策模型,当GPW-VPP 需要同时考虑运营收益最大化和碳排放量最小化时,需要将双目标转换为单目标。 实际上,在追求最大化收益过程时,风电和光伏发电主要用于直接发电上网获取收益,导致电转气设备利用效率降低,造成BPG 和WI 产生的CO2未被处理,产生更多的碳排放;反之,在追求最小化碳排放过程时,风电和光伏发电会被用于进行电转气,从而将CO2转化为CH4,再次用于发电,这会降低风电和光伏发电收益,影响虚拟电厂收益[19]。

由此,最大化运营收益目标和最小化碳排放量目标的优化方向和单位量纲不一致,如何兼容这2 个目标的优化需求,是需要解决的问题。 本文选择模糊满意度理论中的升半直线形隶属度函数和降半梯度隶属度函数,分别用于处理最大化运营收益目标和最小化碳排放总量目标,具体过程如下:

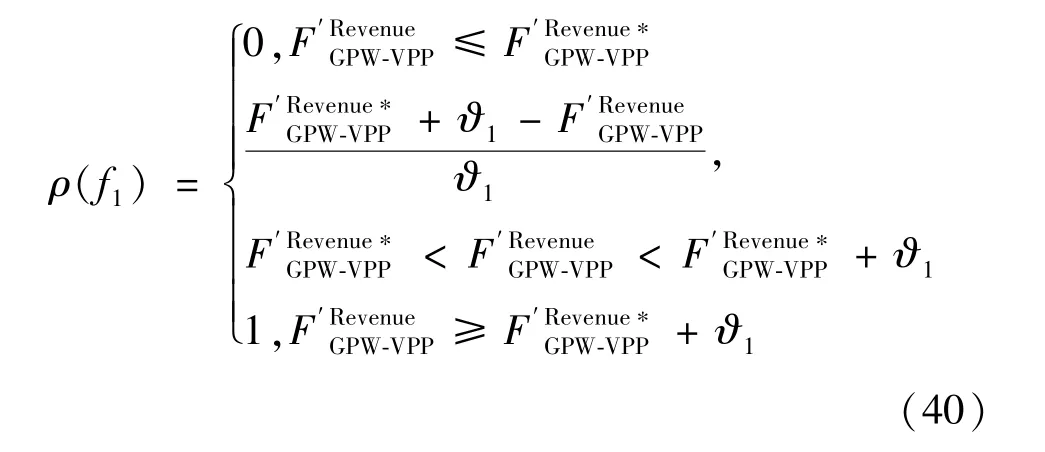
式中:ρ(f1) 为GPW-VPP 最大化运营收益的隶属度函数;为最大化运营收益目标函数的理想值;ϑ1为决策者可接受的最大化运营收益目标函数的增加值,是将目标进行一定的伸缩。

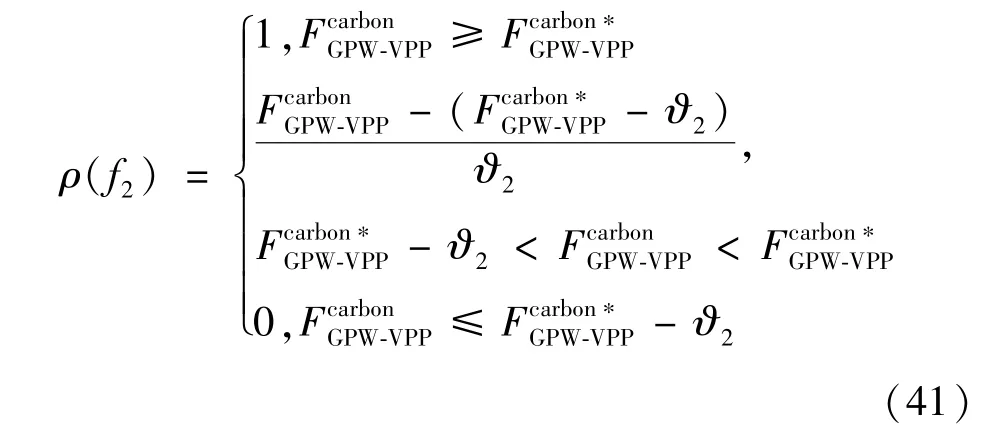
式中:ρ(f2) 为GPW-VPP 最小化碳排放量目标函数的隶属度函数;为最小化碳排放量目标函数的理想值。

根据式(40)、(41),引入决策者预期目标的风险偏差系数σrisk,可将双目标函数转为决策者预期目标函数,具体为:

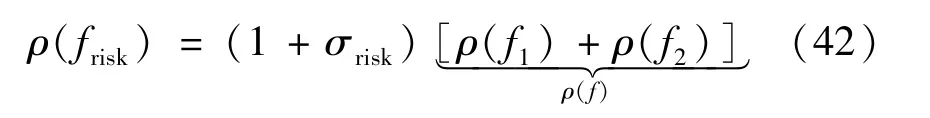
式中:ρ(f) 为GPW-VPP 运营的综合目标函数;ρ(frisk) 为决策者的预期目标值;σrisk为预期目标偏差系数,当决策者目标值ρ(frisk) 高于ρ(f) 时,σrisk取大于0 的值。 根据式(42),GPW-VPP 在考虑不确定性情景下的调度决策值不应高于ρ(f) ,具体约束为:

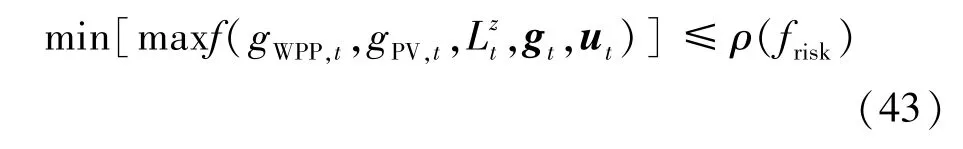
式中:gt、ut表示风光之外的BPG 和WI 在t时刻的出力和启停状态向量。 在满足调峰交易决策成本不高于预期目标ρ(frisk) 的情况下,求解最大不确定性程度α,建立GPW-VPP 随机调度决策模型,具体为:

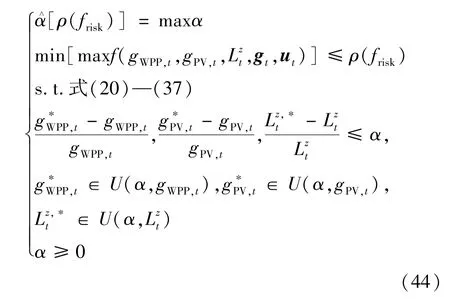
式(44)确立了基于改进IGDT 方法的GPW-VPP运营优化模型,该模型考虑了WPP、PV 和用户负荷不确定性变量的极端情景,保证了所求得的决策方案具有较强的适用性,也可称之为鲁棒性。 但隐含条件是目标函数随WPP、PV 和用户负荷的不确定性呈现单调变化,从而能够利用式(43)进行极值计算。 然而,从式(42)能够看到,GPW-VPP 的决策目标还包括最小化碳排放量优化目标,实际上,WPP 和PV 发电是能产生碳减排效应的,这使得WPP、PV 的不确定性与碳交易成本是相互冲销的,这也使得目标函数随不确定性变量呈现非单调变化,限制了式(44)的适用空间,也就是WPP、PV 发电出力最大或最小场景对应的决策成本不一定最大,此时,就需要建立求取最恶劣情景的方法。

3.3 极端恶劣情景

GPW-VPP 中,当WPP 和PV 实际值低于预测值,而用户负荷实际值高于预测值,且系统净负荷快速增加时,不确定性变量对系统稳定运行的影响将达到最大,即为极端恶劣情景,具体计算为:

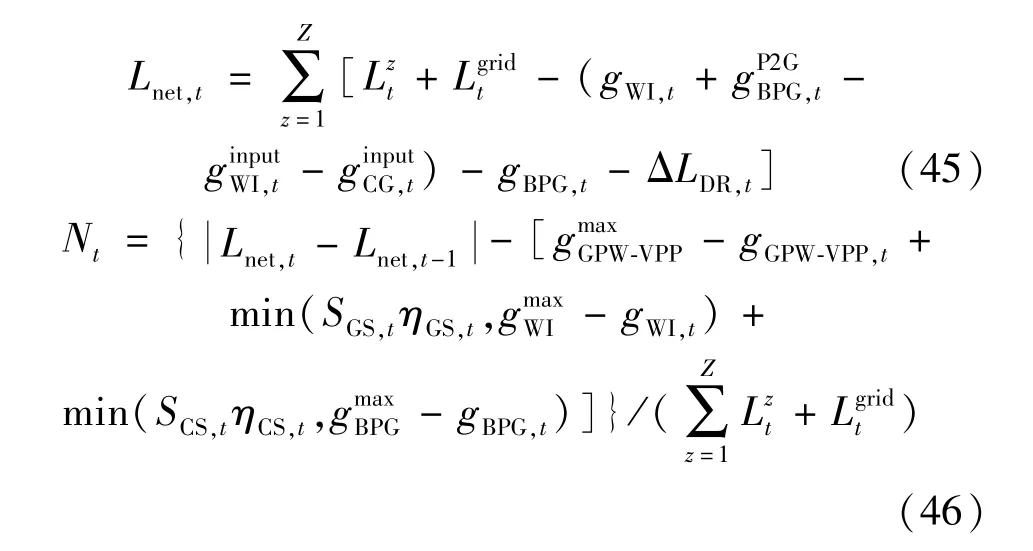
式中:Nt表示t时刻的净负荷波动率;Lnet,t表示t时刻的净负荷需求;表示GPW-VPP 的最大发电能力;gGPW-VPP,t表示GPW-VPP 在t时刻的发电出力;SGS,t表示GS 在t时刻的储气量;表示WI 在的最大发电能力;表示BPG 的最大发电能力;ηCS,t、ηGS,t表示CS 和GS 在t时刻的发电效率。

根据式(46)能够得到净负荷波动性,进一步选择负荷波动程度最大的情景,作为GPW-VPP 运行的最恶劣情景,具体计算为:

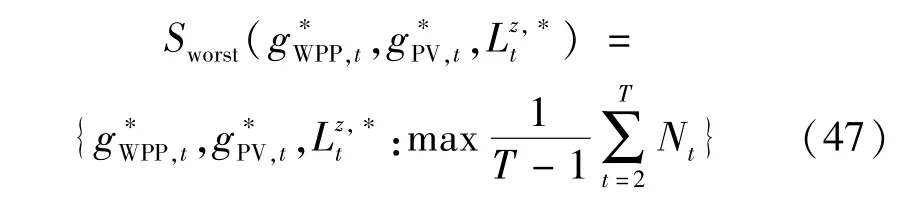
式中:Sworst为GPW-VPP 运行的最恶劣情景。 进一步,构造对应最恶劣情景的GPW-VPP 调度优化决策目标函数,具体为:

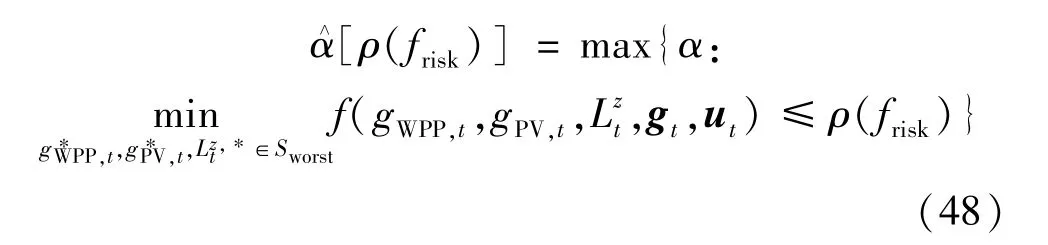
根据式(48)确立了GPW-VPP 在最恶劣情景下交易决策目标。 该情景求取的GPW-VPP 调度优化决策方案为最保守交易方案。

4 算例分析

4.1 基础数据

为对所提模型的有效性和适用性进行验证,本文选择我国兰考能源革命试点为对象,截至2019年底,兰考县新能源装机527.1 MW,其中生物质电厂装机39 MW(秸秆24 MW、垃圾15 MW),分散式风电装机31 MW,分布式装机58.1 MW。 为匹配上述新能源装机规模,本文设定WI 配置45 m3的烟气存储装置,调度周期始末储气量均为0。 表2 为兰考WPP、PV、BPG 和WI 的设备运行参数。

由表2 可知,WPP 和PV 发电成本与发电量正相关,而BPG 和WI 发电成本函数是一元二次函数。 其中,WI 设备参数还包括eWI=0.96、wWI=0.60 和wSP==15 m3/h 和φWI,t=328 元/(MW·h),而BPG 发电输出功率参数∂0、∂1、∂2和∂3分别为-2338.10、323.42、8.46 和26.05。 考虑WI 和BPG就近配置GPPCC 和P2G 设备,GPPCC 设备参数包括gA=15 MW,eCO2,t=0.76 t/(MW·h),λCO2,t =0.23 MW·h/t,ηGPPCC,t的 最 大 值 为 0.9[16],φGPPCC,t=234 元/(MW·h)。 GPPCC 配置80 t 的碳存储装置,碳存储能力为20 t/h。 P2G 设备参数包括ηP2G,t=0.9和φP2G,t=138 元/(MW·h),的最大 值 为 10 MW。 碳 排 放 权 交 易 价格ρCO2,t=689 元/(MW·h)。

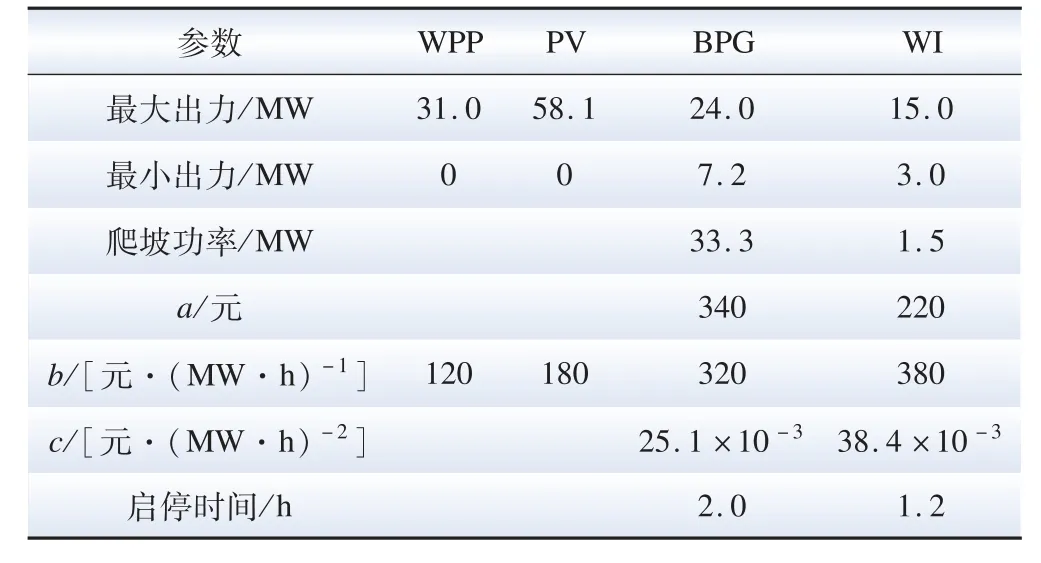
表2 WPP、PV、WI 和BPG 设备参数Table 2 Equipment parameters for WPP, PV, WI, and BPG

2019年,兰考县户籍总数为28.85 万户[20],拥有电动车户占比4%,能够参与GPW-VPP 调度的比重为30%,电动车平均功率为0.35 kW,充电量为21 kW·h。其中,生活用电和农业用电不能参加PBDR,用电价格分别为521.0、464.2 元/(MW·h);小工业用电和电动车用电可参与PBDR,设PBDR 前价格为735.5、769.5 元/(MW·h);PBDR后,峰(08:00—12:00)、平(12:00—00:00)、谷(00:00—08:00)时段价格调整系数分别为1.57、1.00 和0.50 元/(kW·h)。 生活用电、小工业用电和电动车用电参与IBDR 合约响应价格为240 元/(MW·h),提供IBDR 减负荷响应价格为240 元/(MW·h)和IBDR增负荷响应价格为740 元/(MW·h)。 图4 为典型负荷日WPP、PV 的预测出力和不同类型用户负荷需求。

由图4 可知,在白天负荷峰时段,风电可用出力相对较低,而光伏在夜间不出力,彼此间存在互补性。此外,设定GPW-VPP 根据WPP 和PV 的预测出力,将80%总出力作为与电网签订的合同电量,剩余电量通过市场竞价交易完成,合约价格为650 元/(MW·h),违约惩罚价格系统δ=1.8。 设定GPWVPP 的预测精准度为0.92,决策者初始目标偏差系数为0.5,可接受目标函数和的增加值为初始值的0.15。

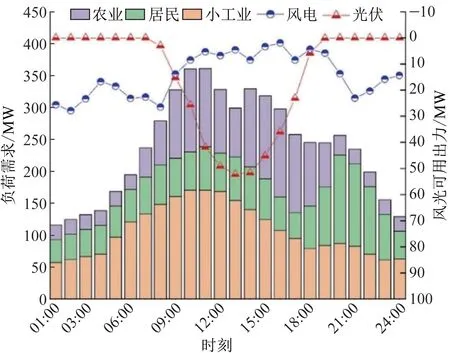
图4 典型负荷日风光预测出力及用户负荷需求Fig.4 WPP, PV forecast output and load demand of different users in a typical load day

4.2 算例结果

4.2.1 方法有效性验证

本节分析常规情景下GPW-VPP 调度优化结果,应用IGDT 方法描述考虑风光不确定性的GPW-VPP调度优化运行,测算不同预期目标偏差系数下的不确定性程度。 图5 为GPW-VPP 可承受不确定性程度与预期目标偏差系数的关系。

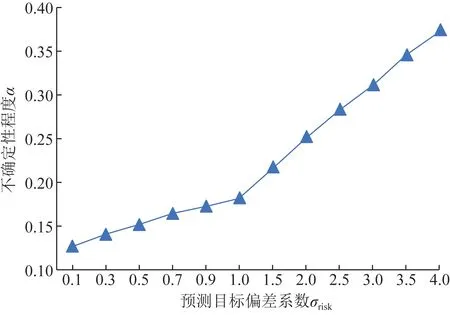
图5 不确定度α 与预测客观系数σrisk的关系Fig.5 Relationship between uncertainty degree α and predicted objective coefficients σrisk

根据图5 可知,不确定性程度与预测目标偏差系数呈线性关系,即随着预期目标偏差系数的增大,决策者能够承受的成本增大,允许的不确定性程度也逐步增加,当预测目标偏差系数为0.5 时,不确定性程度σrisk=0.142,表明不确定性变量实际值在预测值的0.858 ～1.142 范围内波动时,采用本文方法所得决策方案,能保证调度决策方案的成本小于决策者预期成本。

4.2.2 常规情景调度优化结果

基于上述分析,分别对收益最大化、碳排放最小化和综合最优目标函数下GPW-VPP 调度结果进行测算,表3 为不同优化目标下GPW-VPP 运营结果。

表3 不同优化目标调度结果对比分析Table 3 Comparative analysis of results under different optimization objectives

根据表3,当GPW-VPP 按照收益最大化目标运行时,由于BPG 和WI 发电出力可控,不会发生违约惩罚成本,出力相对较高,其产生的更多CO2被GPPCC捕捉,并用于P2G 转换CH4,实现电-气-电循环。 当GPW-VPP 按照碳排放最小化目标运行时,WPP 和PV 发电出力最多,而WI 则未进行发电,BPG 发电下降18%,导致运营收益下降6.61%,但碳排放量最低仅为225.45 t,下降67.11%;当GPWVPP 按照综合最优目标运行时,运营收益仅比收益最大化目标低4.6%,碳排放量比收益最大化目标低35.76%。 由此,在追收收益最大化时,较少风电和光伏发电被P2G 用于转化CO2为CH4,更多用于直接发电上网,导致碳排放量会相对增加,而在追求碳排放量最小化时,风电和光伏发电会更多被P2G 用于将CO2转化为CH4,导致收益相对降低。 在综合优化目标下,VPP 的运营收益和碳排放量均处于单独优化目标,这也说明综合调度方案能够获得更佳均衡的调度策略。 图6 为综合优化目标函数下GPW-VPP运营优化结果。

根据图6,由于PV 在11:00—13:00 和WPP 在17:00—19:00 时段出力较高,导致下调峰需求较大,故EV 提供负的发电出力,增加PV 和WPP 消纳空间,减少碳排放。 同时,PV 在00:00—07:00 和20:00—24:00出力几乎为0,加之碳减排目标限制WI 发电出力,上调峰需求较大,IBDR 提供正发电出力。 对比BPG 和WI,BPG 基本全部按照额定功率运行,WI 则匹配WPP 和PV 发电可用出力,调整自身出力,在谷时段配合WPP、BPG 满足负荷需求。 就GPPCC-P2G来说,GPPCC 捕捉CO2传送到P2G 或存储到CS 中,在谷时段用电较多,峰时段用电较少,间接为GWP-VPP 提供调峰服务,P2G 则维持稳定出力,满足GPW-VPP 负荷需求。 图7 为不同用户需求响应后的负荷变化情况。

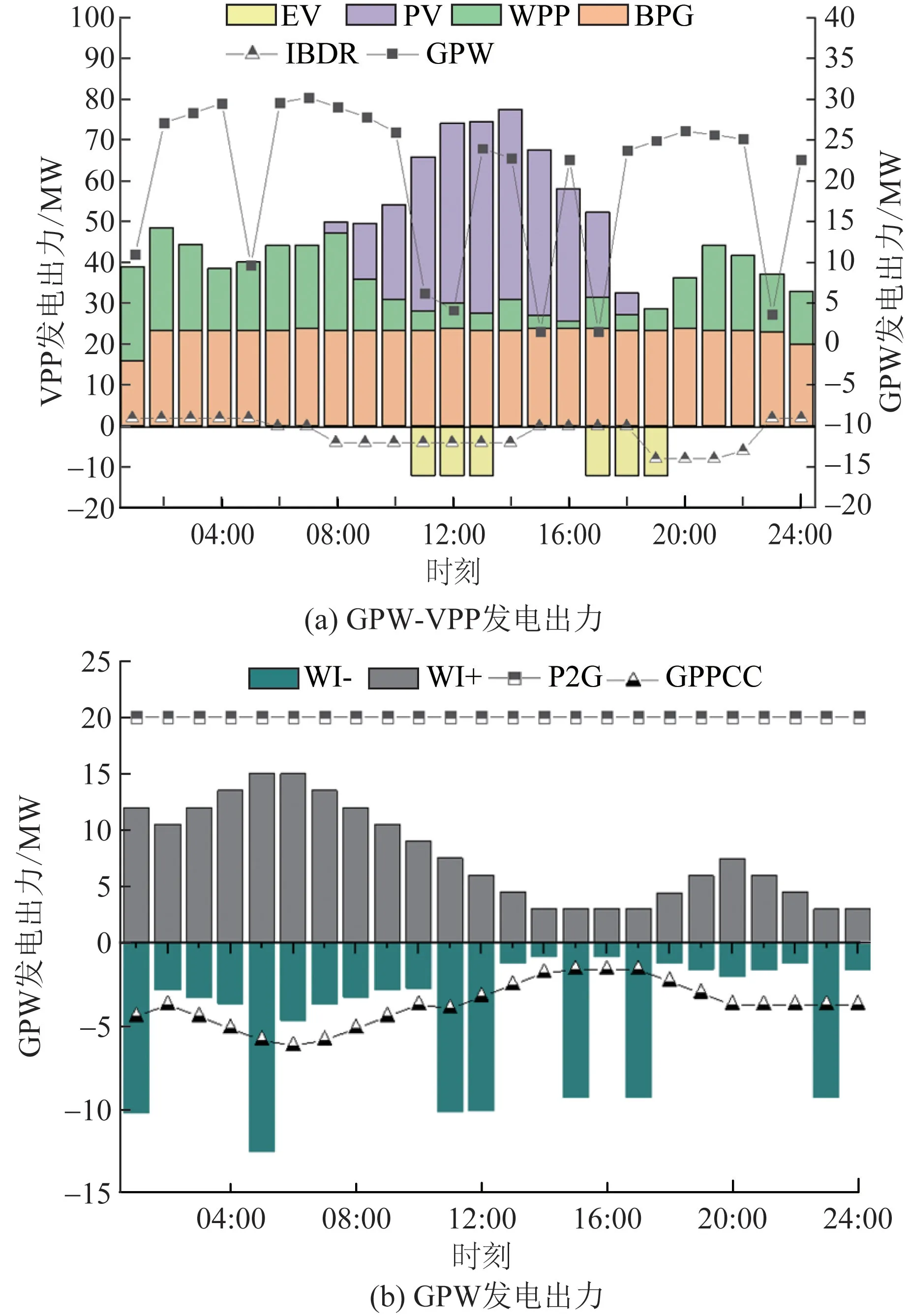
图6 综合优化目标下的GPW-VPP 运行优化结果Fig.6 Operation optimization results of GPW under comprehensive optimization objectives

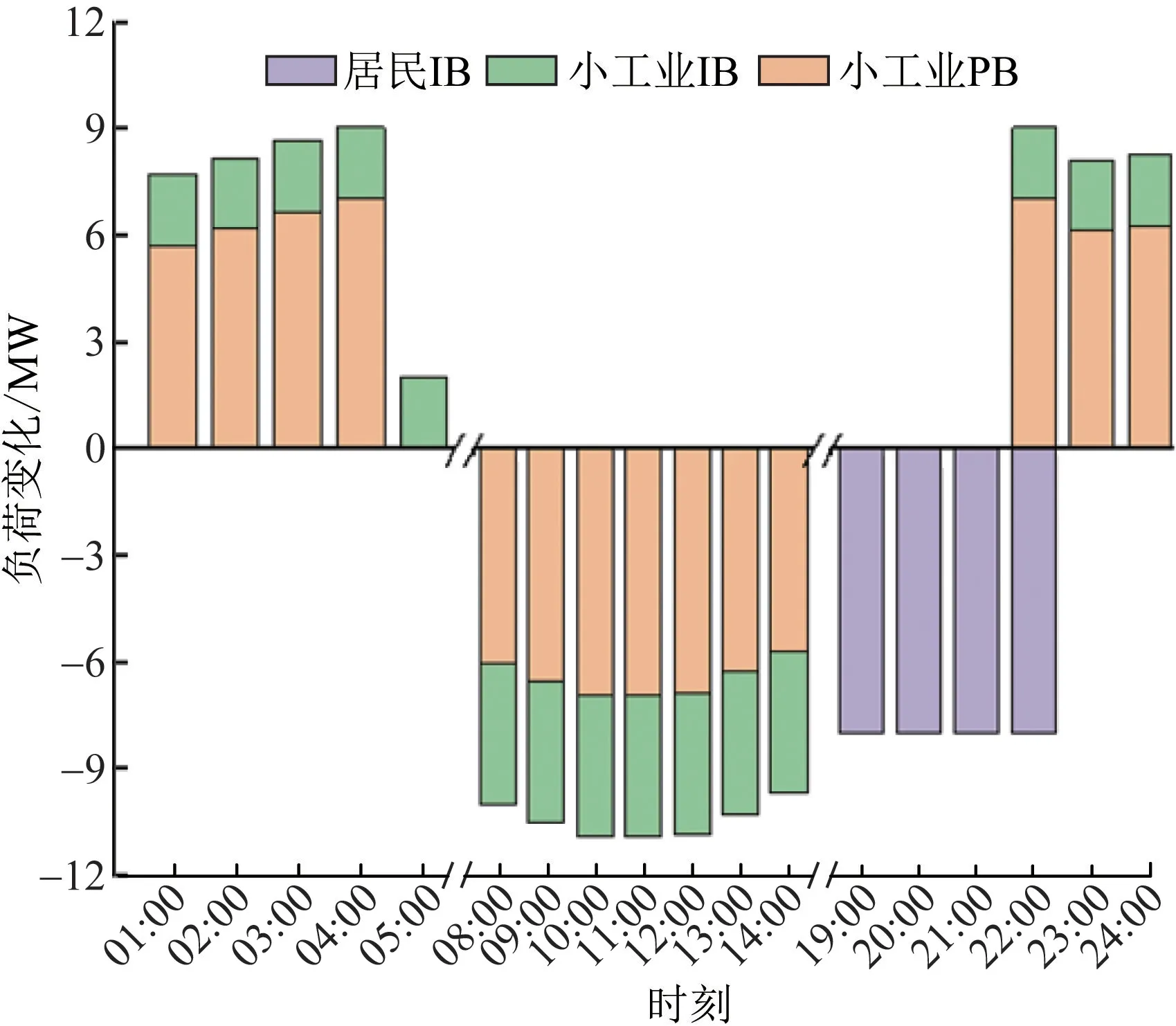
图7 不同用户需求响应出力Fig.7 DR output for different user load

根据图7,小工业用户参与IBDR 和PBDR,在谷时段增加用电负荷,而在峰时段削减用电负荷,其中,小工业用户通过IBDR 产生的负荷变化量分别为16 MW·h和-28 MW·h,而通过PBDR 产生的负荷变化量分别为±45.11 MW·h。 居民用户因其用电属性为必须用电,仅能通过减少用电参加IBDR,总的负荷变化量为-32 MW·h。 此外,CS 和GS 能够通过存储CO2和CH4,在GPW-VPP 需要增加发电时,将其输送至P2G 和WI,满足负荷需求,图8 为综合优化目标下GPW 的烟气流和CO2流。

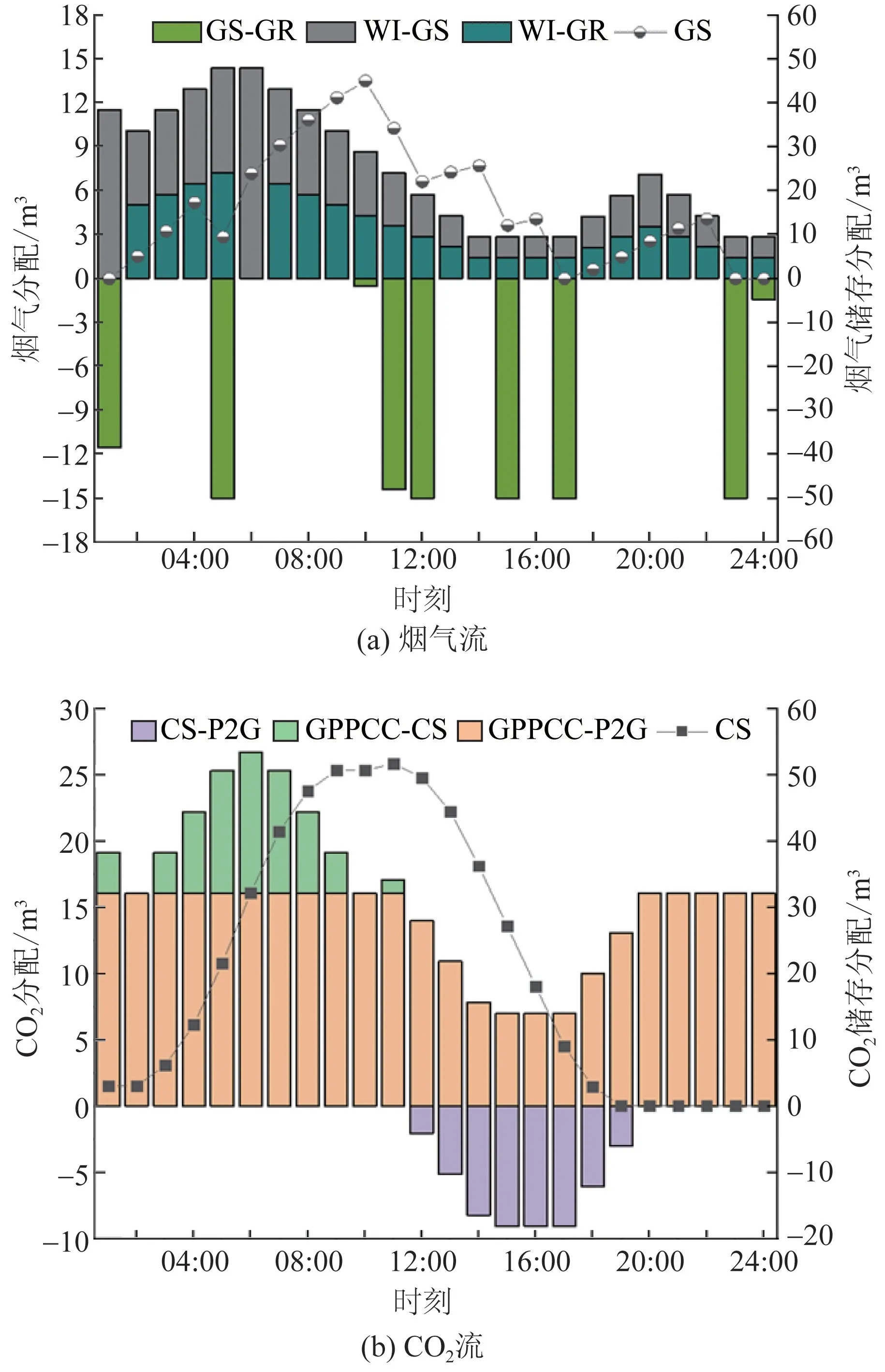
图8 综合运行模式下GPW 烟气流量和CO2流量Fig.8 Flue gas flow and CO2 flow of GPW under the integrated operation mode

根据图8,从烟气流来看,在谷时段,用电价格较低,WI 产生的烟气仅00:00 和05:00 用于发电,弥补WPP 可用出力不足,剩余时段则主要存储于GS;在峰时段,用电价格较高,WI 产生的烟气量较少,GS中烟气用于GR 发电;在平时段,WI 在13:00—17:00将GS 中烟气输送至GR 发电,而在18:00—22:00 用户负荷需求较低,则将产生的烟气存储至CS,在23:00—24:00进入GR 发电。 从CO2流来看,在谷时段和峰时段,GPPCC 捕捉的CO2更大比例用于P2G发电,较少部分存储于CS,实现碳循环利用,而在12:00—19:00,因PV 可用出力逐渐降低,故CS 将CO2逐渐传输至P2G 进行发电,在20:00—24:00,GPPCC 捕捉的CO2则直接用于P2G 进行发电,最大程度实现碳循环利用,降低碳排放量。

4.2.3 极端劣情景调度优化结果

本节对极端恶劣情景下的GPW-VPP 调度优化结果进行分析,同样分析收益最大化、碳排放最小化和综合最优3 个目标下各单元出力结果。 表4 为极端恶劣情景下GPW-VPP 不同目标函数下各单元出力结果。

根据表4,与常规情景一致,综合最优目标能兼顾收益最大化目标和碳排放最小化目标双重需求。但在极端恶劣情景下,为避免WPP 和PV 不确定性给GPW-VPP 带来违约惩罚成本,WPP 和PV 发电出力很低,以综合最优目标为例,相比常规情景,发电出力降低23.84%和22.22%,导致BPG 和WI 提供调峰出力降低,GPPCC 的碳捕捉需求减少。 GPW-VPP总收益仅为38.47 万元,碳排放量为542.6 t,分别变动31.61%和59.38%,这意味着GPW-VPP 更愿意规避WPP 和PV 违约惩罚成本,更高比例调用BPG和WI,导致运营收益降低和碳排放量增加。 图9 为最恶劣情景下GPW-VPP 优化运营结果。

表4 不同目标函数下各单元出力结果Table 4 Output results of each unit under different objective functions

根据图9,相比常规情景,GPW-VPP 调用WPP和PV 发电出力明显降低,对BPG 和WI 的调峰需求降低,GPPCC 和WI 运行过程中消耗的电量也减少,总的发电出力降低, 净负荷曲线的峰荷降低25.81%。 从GPW-VPP 运行结果可看出,GPPCC 基本维持额定功率运行,即3.69 MW,而WI 发电出力基本维持在15 MW 左右,但系统对IBDR 的调用出力要高于常规情景, 正负出力分别为 28、-68 MW·h,表明更多调峰需求由IBDR 满足,最终实现GPW-VPP 最优化运行。

图9 最恶劣场景下GPW-VPP 优化运营结果Fig.9 Optimized operation results of GPW-VPP under the worst scenario

5 结论

针对农村地区存在大量分布式能源,本文将GPPCC、P2G 和WI 与常规虚拟电厂进行集成,形成农村碳捕集虚拟电厂,并针对风电、光伏发电和负荷的不确定性,构造了基于IGDT 的农村碳捕集虚拟电厂近零碳优化运行模型,以兰考农村能源革命试点为对象进行实例分析,得到结论如下:

1)GPW-VPP 能够聚合农村不同类型分布式能源,发挥用户灵活性负荷的调节性功能,最优化利用WPP 和PV 等分布式清洁能源。 WI 通过配置烟气储气装置,可实现发电时间与烟气处理时间的解耦,作为可控负荷参与VPP 优化调度。 GPPCC 能够将BPG 和WI 产生CO2进行捕集,用于P2G 将CO2转化为CH4,进入BPG 再次发电,实现电-碳-电循环。

2)基于IGDT 方法的近零碳调度优化模型能够度量不确定性风险,刻画GPW-VPP 可承受不确定性程度与预期目标偏差系数的关系,制定兼顾收益最大化、碳排放最小化双重目标需求的最优运行方案。 当预测目标偏差系数为0.5,得到不确定性程度σrisk=0.142,表明不确定性变量实际值在预测值的0.858 ～1.142 范围内波动时,能实现决策方案成本小于决策者预期成本。

3)相比单目标运行情景,当GPW-VPP 按照综合最优目标运行时,运营收益和碳排放量相比收益最大化目标分别降低4.60%和35.76%,在极端恶劣情景下,WPP 和PV 出力降低23.84%和22.22%,GPWVPP 的总收益和碳排放量分别变动31.61%和59.38%。