五轴数控系统的旋转轴速度规划方法*

黎永杨 刘远凯 王科 葛鹏遥 黄国辉

（①深圳众为兴技术股份有限公司，广东 深圳 518052；②上海新时达电气股份有限公司，上海 201802）

五轴数控加工中心作为高端精密设备的代表之一，已被广泛应用于航天结构件、叶轮叶片和大型精密模具等零件的加工[1]。相对于三轴系统，由于两个旋转轴的增加，无疑对速度控制提出了更为复杂的要求[2]。在数控系统中，工件坐标系下刀具进给速度控制是实现产品高速高精加工的关键环节，可直接影响到产品的出厂合格率。五轴数控系统若以旋转轴线性跟随平动轴的方法进行加工，容易引起旋转轴速度跳变、加速度超限等问题，致使机床产生冲击，进而因为运动学的反解计算导致刀具姿态偏离所设计的平面，从而产生非线性误差[3]。

为避免旋转轴速度跳变发生，提高五轴数控系统的加工质量，陈良骥等[4]基于对旋转轴角速度/角加速度的约束控制，在计算出平动轴实际最大可达速度/加速度后再进行平动轴的速度规划，但该方法未考虑多段连续轨迹加工情况，不具有普遍适用性。闵莉等[5]提出了一种通过对比刀轴矢量变化率选择性的调整刀轴矢量的方法，以保证加工带宽并使得刀轴矢量的变化保持平滑，该方法仅适合应用于加工程序的后处理器中，对于操作人员的要求也较高。杨敏等[6]以弓高误差、刀具的进给运动和驱动轴的运动性能为约束，建立基于时间最优的五轴机床速度规划模型，并以拟牛顿法为基础设计了具有鲁棒性的速度曲线求解策略。钟泽杉等[7]基于机床的运动学反解，推导了驱动轴的速度、加速度、跃度与进给速度的映射关系，以加工效率为优化目标，建立多约束条件下高维度非线性最优化模型，应用序列二次型规划（SQP）方法分阶段求解，提出了一种考虑驱动轴性能限制的进给速度规划方法。上述两种方法实现了加工速度的连续控制，但需要提前离散化采样，计算量大而复杂，而普通的嵌入式数控系统性能有限，必须牺牲插补周期来获得较好的控制性能，不利于五轴数控系统的大面积推广应用。

为了解决现有五轴数控系统的工程实际问题，综合考虑控制器成本、计算复杂程度和机床多维度冲击保护等因素，本文拟采用计算简单、易实现及运算效率较高的数学模型来实现五轴数控机床中旋转轴柔性速度规划的目标。

1 旋转轴速度规划方法

以AC摆台型五轴数控机床为例，平动轴为X、Y、Z轴，另外包含A旋转轴和C旋转轴，基于时间同步的原则，利用平动轴的运动时长约束实现对旋转轴的速度规划。旋转轴的速度规划，其中起步速度的值等于前一线段运动的末速度，另外需要通过计算确定加速度、驱动速度和末速度的大小。

1.1 运动时间计算

假设存在两条直线做连续插补运动，根据平动轴在第m段运动指令的运行参数和位移量，可得目标最大速度

其中：Δlmp、vsml、veml、aml分别为平动轴在该段指令的位移量、起步速度、末速度和加速度。将平动轴的目标最大速度vm与预设最大速度vcml进行比较，存在两种情况：

（1）当目标最大速度vm小于或等于预设最大速度vcml，平动轴的运行时间t为

（2）当目标最大速度vm大于预设最大速度vcml，平动轴的运行时间t为

基于机床插补运动时平动轴和旋转轴时间同步的原则，由式（2）、式（3）综合分析所得时间t即为旋转轴的运动时间。

1.2 末速度和加速度初算

设vemA、amA、ΔlmA分别为第m段加工指令中A旋转轴的末速度、加速度初值、位移量，Δlm+1A为第m+1段加工指令中A旋转轴的位移量，存在两种情况：

（1）当Δlm+1A>0，则第m段加工指令A旋转轴的末速度vemA和加速度amA为

（2）当Δlm+1A=0，即A轴没有运动量，则有

由式（4）、式（5）综合分析可得旋转轴运动的末速度和加速度规划参数初值，其中初始加速度amA用作后续临界位移长度计算。

1.3 参考临界位移长度计算

由式（1）～（5）可知，当A旋转轴运动时间t、起步速度vsmA、末速度vemA和位移量ΔlmA已知的情况下，其速度规划时用到的驱动速度和实际加速度需要根据不同情况做出调整，本文使用临界长度L1、L2、L3、L4作为判断条件。

（1）当A旋转轴在运行时间t内，以起步速度vsmA和初始加速度amA先加速后减速到末速度vemA时，可得临界长度L1为：

（2）当A旋转轴在运行时间t内，以起步速度vsmA或末速度vemA作为最大速度时，可得临界长度L2为

其中：Vse取值为max(vsmA,vemA)。

（3）当A旋转轴在运行时间t内，从起步速度刚好加速或减速到末速度时，通过比较运行时间t内A旋转轴的起步速度和末速度，可得临界长度L3为

（4）当A旋转轴在运行时间t内，先减速到0，再加速到末速度时，通过比较运行时间t内A旋转轴的起步速度和末速度，可得临界长度L4为

1.4 调整后的驱动速度和加速度计算

由式（6）～（9）得到A旋转轴的4个临界长度L1、L2、L3、L4作为判断条件，将A轴的位移量ΔlmA和4个临界长度进行比较，存在5种情况计算A旋转轴的目标驱动速度NewVc和目标加速度NewAcc。

（1）当ΔlmA>L1时，可得方程组

（2）当L2<ΔlmA≤L1时，可得方程组

（3）当L3<ΔlmA≤L2时，可得方程组

（4）当L4<ΔlmA≤L3时，可得方程组

（5）当ΔlmA≤L4时，可得方程组

根据不同情况，由式（10）～（14）方程组的解，即可计算得到目标驱动速度NewVc和目标加速度NewAcc的值。

至此，A旋转轴速度规划时需要用到的起步速度、加速度、驱动速度和末速度参数都已确定，后续通过周期插补输出脉冲指令给各关节伺服执行，即可实现五轴数控机床的运动控制。

需要补充说明的是，当调整后的驱动速度、加速度值超出机床相关的运动学约束阈值参数时，为避免相关运动轴出现超限报警的情况，须使用如式（15）所述平动轴与旋转轴之间关系模型，来降低平动轴的运动时间t，使得旋转轴运行在合理的阈值参数范围内。

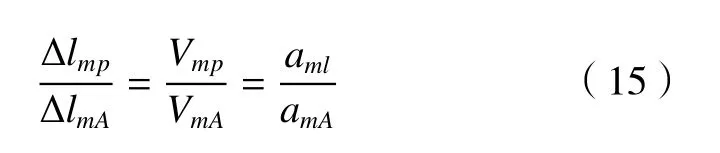
其中：Vmp为平动轴在第m段的驱动速度，VmA为A旋转轴在第m段的驱动速度，其他变量在本文已有叙述。

同理可求得C旋转轴的规划参数，来实现对C旋转轴进行相应的加减速控制规划。

2 旋转轴速度规划流程

在五轴数控系统底层的运动控制规划中，把旋转轴规划参数计算融合在平动轴的速度前瞻里面，计算得到合理的运动参数，通过梯形加减速[8−9]插补计算后发脉冲指令给伺服驱动器执行，即可实现五轴数控机床的运动控制，具体规划流程如图1所示。

通过如图1所述规划流程，在工件加工过程中，各关节能够获得合理的加减速规划参数，为后期机床进行的高精度工件加工打下坚实基础。

图1 五轴数控系统的速度规划流程

3 实际实验

为了验证本柔性控制方法的有效性，基于如图2所示摆台型五轴数控机床进行了相关实际实验。该机床包括两个旋转轴，第一旋转轴（C轴）和第二旋转轴（A轴），工作台固定连接在第一旋转轴上。

图2 摆台型五轴数控机床

如图3所示，选取数控加工文件中连续的一条直线和一个相切圆弧，作为待插补路径进行速度规划计算。假设直线段A旋转轴旋转0°，圆弧段A旋转轴旋转30°。

图3 平动轴插补轨迹路径图

设置五轴数控机床相关的运动学约束参数：平动轴预设最大速度vcml=50 mm/s，最大加速度aml=200 mm/s2，数控系统采样插补周期T=0.002 s，平动轴的起步速度vsml=2 mm/s，平动轴的末速度veml=1 mm/s。实时采集控制过程数据，当旋转轴采用线性跟随平动轴运动时，得到的速度曲线图4所示，而经过本文如图1所述速度规划流程，得到速度曲线如图5所示。

图4 线性跟随运动时速度曲线

图5 基于时间同步规划后的速度曲线

图4所示平动轴的速度曲线采用梯形加减速算法进行控制规划，旋转轴采用线性跟随平动轴运动方式，在直线和圆弧拼接处旋转轴速度存在明显的速度跳变问题。图5所示旋转轴速度曲线经过重新规划，使得旋转轴在与平动轴运动时间同步的基础上保持了速度连续，解决了旋转轴速度跳变的问题，各关节在可控范围内运动，成功避免了机床冲击的出现，符合实际的加工需求，也有利于延长机床使用年限。

4 结语

本文以工程实际技术问题为背景，基于时间同步的原则，利用平动轴的运动时长约束实现对旋转轴的速度规划，计算得到旋转轴合理的起步速度、加速度、驱动速度和末速度值，并通过梯形速度规划插补输出给伺服电机执行，给出了计算量少、易于在嵌入式五轴数控系统中实现的旋转轴柔性速度规划技术方案。从实验结果的对比分析可知，本方法避免了旋转轴采用线性跟随平动轴运动时出现的速度跳变问题，多段连续轨迹插补时也能保持旋转轴的速度连续，有利于提高工件加工质量和延长机床使用年限。该速度控制方案已成功应用于五轴数控系统中，并已在高精密点胶、抛光打磨和自动光学检测行业中投入了实际应用。