一种双信标机制下的指纹库构建方法

秦宁宁，吴忆松，孙顺远

(1.江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡 214122；2南京航空航天大学 电磁频谱空间认知动态系统工信部重点实验室，江苏 南京 211106)

近年来，随着通信技术的进步，室内位置服务研究得以飞速发展。受GPS工作局限与固件配置约束的影响，以信号能量为尺度的指纹定位方法成为室内定位技术研究的重要方向。虽然该方法回避信号载体差异与内容细节，但是定位精度不可避免地易受离线指纹库构建的速度与效率影响[1]。

室内定位的指纹库构建方法多种多样，例如全采法、众包法和预测法等[2]。全采法的思想是在室内场景中规划无线接入点(Access Point，AP)和指纹点位置后，采集并处理得到各个指纹点处来自各无线接入点的信号强度均值数据，与其物理坐标构建组成指纹库。尽管利用全采法构建的指纹库精度较高，但对给定大面积定位区域时，该方法会带来大量采集成本消耗，因此实用性较差。为缩减采集成本，众包法[3]结合群智感知理论，利用系统用户的移动设备采集并上传指纹数据，但用户数据本身不精准的位置坐标极大地限制了众包法的推广应用。

相比于全采法与众包法繁复的离线采样与建库方案，预测法将部分指纹点标记为信标，仅需采集信标处RSS，挖掘信标信号间的深层关系来预测非信标指纹点的RSS，极大地减小了建库开销[4]。常用的预测法目前有空间插值法[5]和矩阵填充法[6]。作为典型的空间插值法，反距离加权(Inverse Distance Weighted，IDW) 算法逻辑简洁，位置权重仅与物理距离负相关，但对多干扰源的复杂场景的预测不精确；而克里金(Kriging)算法在预测前需要拟合场景相关的变异函数，由此带来计算复杂、结果波动率高的缺陷[7]。为平衡计算复杂度，文献[8]采用泛克里金插值法对位置指纹进行预处理，但减少的人工和时间成本有限，且构建精度受变异函数的影响较大。文献[9]因势利导地利用RSS特征设计IDW预测指纹库，但受IDW算法粒度较粗的属性影响，精度改善效果不明显。矩阵填充方法是利用定位场景中指纹点位置在物理距离层面的强相关性，为高维指纹库数据降秩，从而更快捷地预测空缺指纹数据。文献[10]和文献[11]在离线阶段扩充指纹库时都引入了矩阵填充法，对比其他构建方法后均发现，矩阵填充法普遍依赖大量信标信息，从而未能充分发挥预测法省时省力的优势。

融合反距离加权的简单易行，引入径向基神经网络深层联系特征，笔者提出一种基于双信标的径向基位置指纹库构建算法(Dual Beacon-Radial Basis Function，DB-RBF)，以拉丁超立方抽样(Latin Hypercube Sampling，LHS)确立主次双信标点的机制，来减少采样信标数量；利用反距离加权和径向基神经网络(Radial Basis Function Neyral Network，RBFNN)来预测未知接收信号强度信息。DB-RBF相比全采法牺牲可接受范围内的指纹库精度与定位性能，从而节省了大量人力与时间成本的建库开销。

1 理论模型

1.1 拉丁超立方抽样

拉丁超立方抽样是一种从多元参数分布中近似分层随机抽样的技术，其关键是对输入概率的分布进行分层。基于单一维度上抽样概率相等的区间要求，拉丁超立方抽样要求在给定D维空间中，将每个维度均等地划分为v个不重合的区间，实现在各维度抽样区间内随机获取一个样本值，恰好构建成v个抽样样本。

1.2 接收信号强度的反距离加权插值

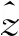
(1)

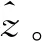
若给定场景内有信标点集合ΩB，包含L个信标点PB l(l=1，2，…，L)，则将反距离加权映射到该室内场景，在已知坐标为(xl，yl)的信标点PB l处，采集来自于无线接入点的接收信号强度，与其坐标组成指纹信号：

PB l={(xl，yl)，rl} ，

(2)

其中，rl表示PB l接收到来自无线接入点的接收信号强度。若场景内包含F个待估计点PEf(f=1，2，…，F)，则可得到坐标为(xf，yf)的PEf相应的指纹信息为

(3)

(4)

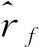
1.3 径向基神经网络插值

径向基神经网络是一种三层神经网络，其包括输入层、隐含层、输出层。径向基神经网络的插值结果最少只需由一个中心点即可确定，因此将其应用于稀疏信标的指纹预测场景中，可充分发挥其小尺度指纹库优势。

在定位场景中，径向基神经网络预测任意一个PEf的接收信号强度仅依赖于PEf与各PB l之间的关系范式‖PEfPB l‖，基函数g可表示为

g=φ(‖PEfPB l‖) ，

(5)

其中，‖PEfPB l‖通常可以构造为欧式距离、余弦相似度和皮尔逊相关系数等。在已有ΩB的情况下，已知信标点PB l的指纹信息，可以利用径向基神经网络插值模型预测PEf的RSS为

(6)

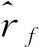
为了求得给定场景下的ω，可通过将信标点集合ΩB作为测试样本集，代入式(6)，则存在关系式：

r=φω，

(7)

其中，r=[r1，r2，…，rl，…，rL]T，为已有信标点的接收信号强度矩阵，φ为基函数矩阵：

(8)

由此，可解得权重系数矩阵：

ω=φ-1r。

(9)

2 双信标机制

指纹库构建过程中信标点与待估计点的比例选取很大程度决定了构建效率。若信标点比例过小，则会导致最终的指纹库与真实指纹偏差较大，无法用于室内定位；若信标点比例过大，则又会导致指纹库扩张不充分。为了灵活调整指定场景下的信标点比例，引入双信标机制，寻求平衡指纹精度和扩张效率的最优信标点比例。

2.1 确定主次信标点位置

为构建参考指纹信息，首先要选取合适的抽样方法确定场景中部分位置作为主信标点。鉴于所有信标地位平等的特征，非概率采样方法因其样本概率的差异性而不宜采纳；而在等概率抽样方法中，简单随机抽样可能无法选出足够多代表场景特性的主信标点，整群抽样方法的结果集位置又过于集中。以拉丁超立方抽样为代表的分层抽样方法兼顾随机性与均匀性，是定位场景选取初始信标点的最佳选择。

在给定Ω=sasb，(sa≥sb)的矩形区域内，选取一定比例的主次信标点位置。完全随机地选取信标点具有偶然性，不能很好地反映指纹库构建算法的构建效果，均匀地选取则费时费力。基于室内定位场景的独特性，对给定Ω区域，采用改进的拉丁超立方抽样获取主次信标点。

步骤1 初始化。划分数量v，迭代次数Z，信标点集合ΩB=∅，主信标点集合ΩM=∅，次信标点集合ΩS=∅；

步骤2 将sa边均等分为v段区间Ai(i=1，2，…，v)，取Ai中点作为区间代表位置，编号i；

步骤3 将sb边均等分为u=[vsb/sa]段区间Bj(i=1，2，…，u)，取Bj中点作为区间代表位置，编号j；

步骤4 将编号满足i为奇数的位置(i，j)选为信标点PB l(l=1，2，…，L)，并聚类到ΩB；

步骤5 分别令i=1，3，5，…，不重复产生随机数j∈[1，u]，标记位置(i，j)为主信标点PM。重复此步骤Z次，得到P=[Zv/2]个主信标点PMp(p=1，2，…，P)，并聚类到ΩM；

步骤6 将ΩB中未被选为PMp的位置(i，j)记为次信标点PSq(q=1，2，…，Q)，即PSq∈ΩB且PSq∉ΩM，并聚类到ΩS；

在定位场景内采用拉丁超立方抽样的方法确定一定比例的主次信标位置，对主信标采集信号强度作为其指纹信息，以反距离加权估计次信标信号强度。图1为利用该算法确定主次信标位置及信号强度过程的示意图。以v=14，Z=6时主次信标拉丁超立方抽样示意图为例，如图2所示。图中标注的位置(7，6)表示第3轮迭代时选中的主信标点之一，而位置(11，6)属于ΩB且未被抽为PMp，因此标记为次信标点。由抽样结果可以看到，拉丁超立方抽样确保任意维度的任意区间之间样本数量差不超过1，其分层抽样特征属性可以以公平概率的方式抽取信标，且能支持多次重复进行，在兼顾抽样公平代表性的同时，能消除构建信标集合的偶然性。

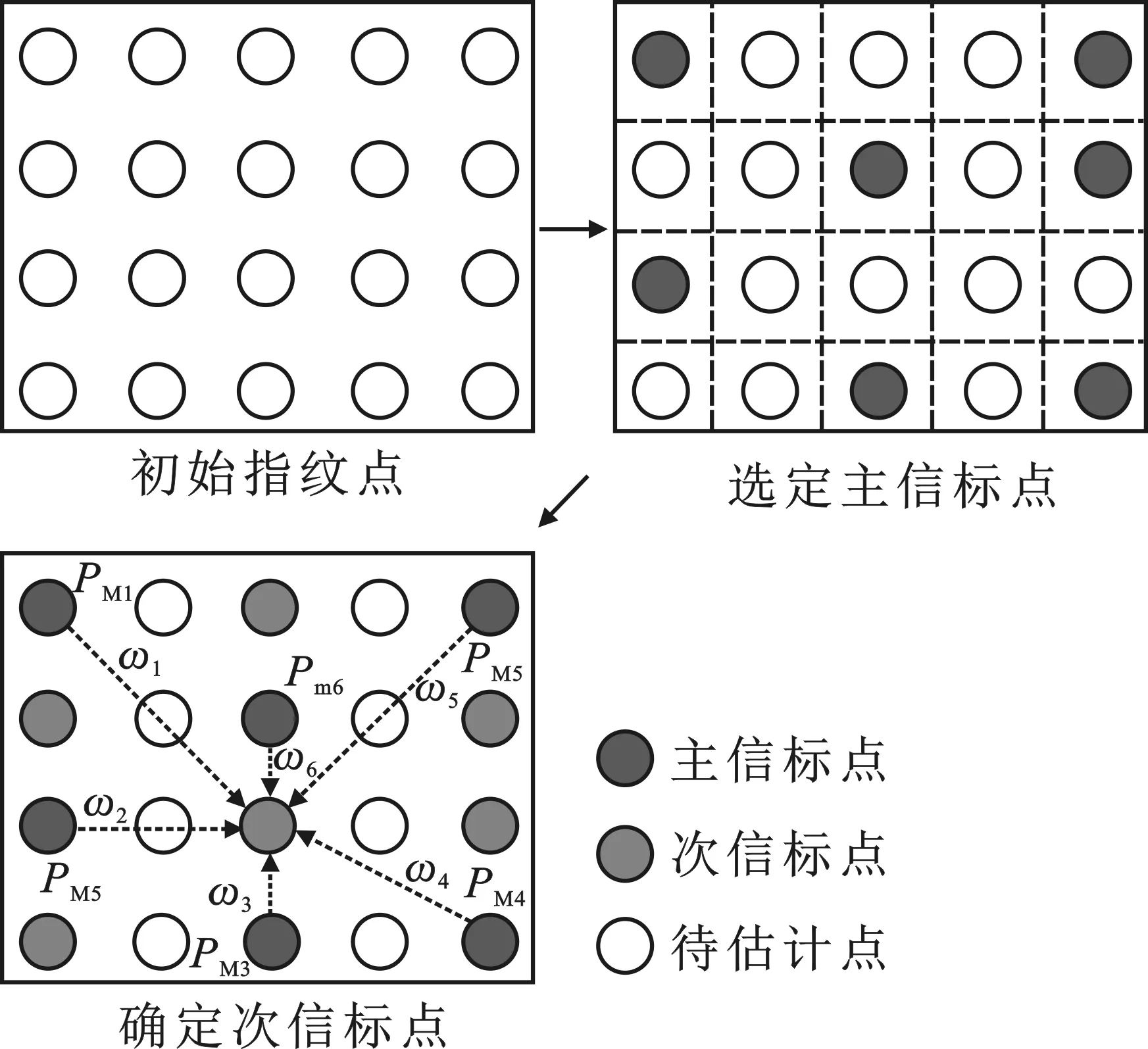
图1 双信标指纹确定过程示意图

图2 v=14，Z=6的LHS抽样示意图

2.2 确定主次信标点RSS信息

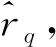
(10)

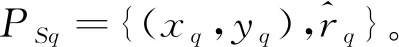
通过上述插值过程，已经具备完整的双信标指纹信息。由抽样过程可知，信标点集合ΩB由ΩM和ΩS组合而成，即三者存在如下关系：

(11)

其中，信标点PB l的序号满足1≤l≤L=P+Q。

3 指纹库扩充

由于反距离加权插值算法只考虑到信标点的位置相关性，未能充分利用数据的空间相关性，因此对于预测距离较远的未知点信息贡献不大。众所周知，神经网络算法具有极强的非线性映射能力，理论上只要隐层神经元数目足够多，神经网络能以任意精度逼近一个非线性函数。而神经网络方法的缺陷在于，只有在信标点信息达到一定数量的情况下，才可以充分利用数据间的相关性和全局性，保证较高的预测精度。因此，为了保证指纹库的构建精度，同时减小建库的人工和时间成本，DB-RBF选择借助反距离加权预测少量次信标点的指纹信息，而在大幅扩张指纹库阶段采用更为精准的神经网络方法来插值。在最常用的神经网络算法中，反向传播神经网络(Back Propagation Neyral Network)存在神经元数目太多导致网络过适性的缺陷[12]，因而具有更强的输入输出映射功能，且学习过程收敛速度快的径向基神经网络更适合预测指纹点的接收信号强度[13]。

RBF能够在选取一定范围的参考点作为已知量下，依次对标记点上来自同一个无线接入点的接收信号强度拟合信号曲面。在遍历完所有无线接入点后，即可完成对指纹点上接收信号强度向量的估计。

由于指纹定位场景中PB l与待估计点PEf的信号量以物理距离呈现强相关性，因而文中将基函数g的自变量‖PEfPB l‖构造为两点之间的坐标欧式距离，即

φ(‖PEfPB l‖)=φ(dfl)=φ(((xf-xl)2+(yf-yl)2)1/2) 。

(12)

基于式(6)，式(12)在求解权重系数ωl(l=1，2，…，L)中得到

(13)

考虑室内环境复杂，无线接入点信号波动等因素，已测ΩB很难完全覆盖待估计点的信号特征。因此在实际的插值逼近问题中，需要对基函数进行调节。引入调节参数β，更新基函数φ(dfl)=(dfl2+β)1/2，代入式(13)，得

(14)

由式(9)可解得权重系数矩阵ω，代入式(6)，即可求解PEf来自相应无线接入点的接收信号强度。

4 实验与结果分析

4.1 实验场景

实验环境为如图3所示的江南大学物联网工程学院某办公室，定位区域总面积为9 m×7 m。从图3可以看到，室内布置了较多办公桌椅，符合一般室内环境的静态干扰条件。定位区域内规划指纹点间距d0=1 m，指纹点总数N=80。室内包含I=12个iBeacon蓝牙节点[11]，型号为寻息m0u，发射功率选用-20 dBm。将蓝牙节点作为无线接入点放置在图3中的位置，标记为AP1，AP2，…，AP12。为了分析论文算法建立的位置指纹库与实际指纹库的误差，文中先采用全采法构建位置指纹库，选用安卓手机作为采集端对定位区域内所有参考点进行接收信号强度值的采集。同时考虑到接收信号强度数据的时变性，为保证获取到的接收信号强度数据的准确性，对每个参考点采样100次，平均采集时间t约为3 min。由于室内环境的干扰，采集到的信号会有较多偏离值。对于信号滤波技术的选取，考虑到与对比算法保持公平性，采用普遍适用的高斯滤波[14]，将滤波处理后的数据样本求几何平均值作为每个参考点的接收信号强度信号。

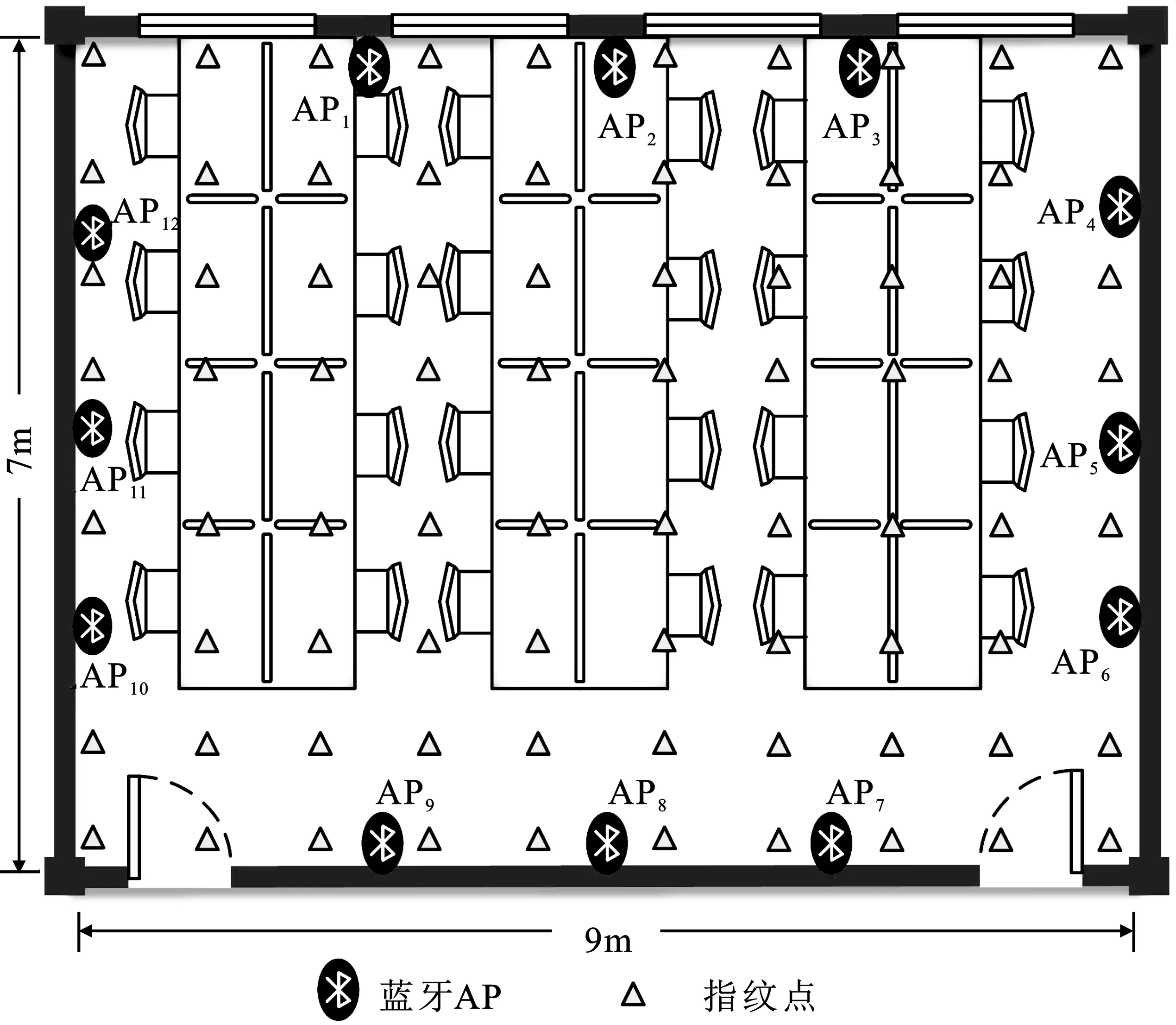
图3 实验场景示意图

4.2 抽样稳定性对比

为了验证文中算法采用的拉丁超立方抽样方法的稳定性，实验对比了完全随机抽样与拉丁超立方的抽样结果对定位精度的影响。为保证对比的公平性，两种抽样方法得到的信标点均用反距离加权进行插值和加权最近邻节点算法(Weighted K-Nearest Neighbour，WKNN)定位测试。以平均定位误差e来衡量定位精度：

(15)

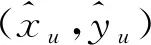
在节4.1的定位场景下，分别采用完全随机抽样与拉丁超立方抽样在Z=5的情况下重复试验80次。图4为实验结果的概率分布对比图。

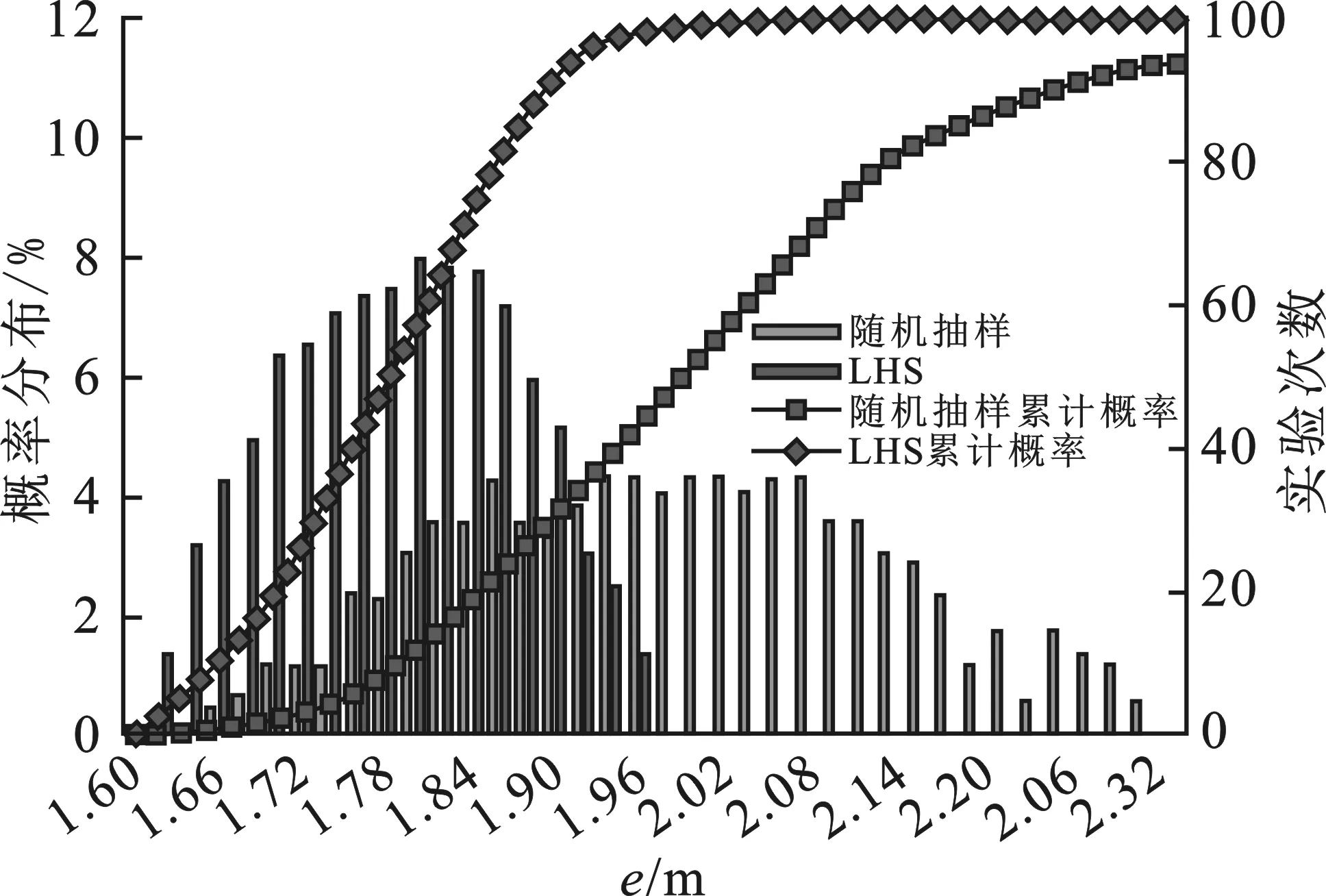
图4 两种抽样方式的定位稳定性对比

表1为定位效果的对比。可以看出，两种抽样方法获得的最低定位误差分别为1.60 m和1.65 m，差异比仅为3.1%。但是随机抽样容易出现极大误差值，最高为3.21 m，同时随机抽样结果的方差26.7远大于拉丁超立方抽样的8.5，其数值波动幅度和范围较大。相反地，拉丁超立方抽样能够在信标点比例可控的前提下，给后续插值与定位工作提供稳定高效的主信标选择方案。

表1 两种抽样方式的平均定位误差对比

4.3 径向基神经网络插值

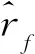
4.3.1 插值效果分析

径向基神经网络插值的优势在于能够充分利用已有少量信标点互相之间的联系，批量快速地估测到平面内任意位置的接收信号强度信息。论文利用这一特点将指纹点的间隔缩短为0.2 m，得到覆盖整个定位场景的指纹信息。不失一般性，图5以来自AP12的指纹信号预测结果为例，展现径向基神经网络插值结果，其中主次信标点位置以圆形离散点表示，预测所得的指纹数据以三维热度图的形式展现。图中信号曲面整体具备高斯分布的特征，预测结果受经典信号传播模型约束；曲面中也包含若干个局部范围的信号波动，可见文中插值方法真实反映了场景内干扰源的位置及强度，能提供符合个体特征的指纹数据。

图5 RBF预测信号热图

4.3.2 调节参数β取值分析

参数s主要影响基函数φ(df l)的取值，从而影响径向基神经网络插值精度。为了得到具备场景特性的参数β，实验对比了不同β取值下，径向基神经网络插值结果对e的影响。如图6所示，β从0开始，以0.05为步长间隔向上寻找本场景下最优定位精度时的匹配取值。当β≤0.25时，φ(df l)受到β的调节作用并且e随着β增大而减小；但β>0.25后，实验得到误差随β增大而陡增，对于基函数的调节起负作用。不失一般性地，β的取值范围为[0，0.4]。

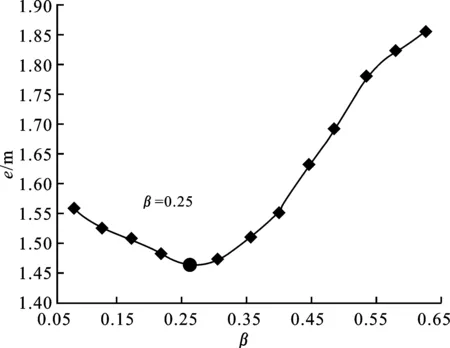
图6 β与定位误差

4.3.3 误差对比

为了分析经DB-RBF插值得到的接收信号强度信号的准确性，实验对比了IDW、SA-ABC-Kriging[15]以及DB-RBF的插值结果与真实测量值之间的误差，如图7和图8所示。对比可知，反距离加权的插值结果整体比真实测量值偏小，平均误差达到4.2 dBm，这与其信标点权重体系固定的插值策略直接相关，固定的加权幂指数ρ使得部分位置过度参考远距离信标点。而SA-ABC-Kriging所得预测值误差波动较大，存在若干偏差达到7 dBm的点，对指纹库构建精度影响严重。通过DB-RBF插值所得的指纹数据与真实测量值较接近且误差变化幅度小，计算得到平均误差为2.21 dBm，较小的误差换来极大的人工成本节省，径向基神经网络插值能够在保证插值准确性的同时快速构建指纹库。

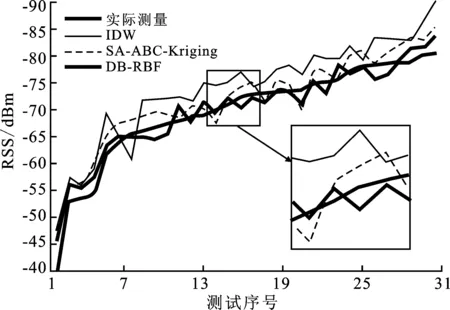
图7 预测值与测量值对比

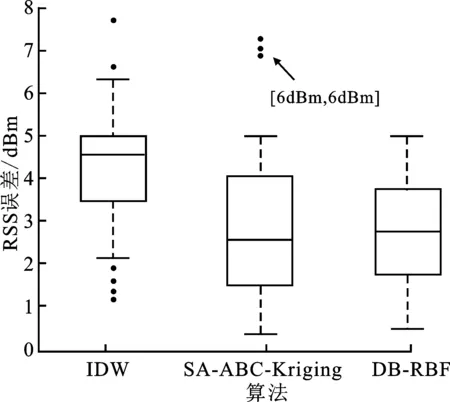
图8 算法间预测误差箱型图

4.4 定位精度对比

为验证DB-RBF信号预测对定位效果的影响，本实验对比了无插值、IDW、SA-ABC-Kriging、DB-RBF、全采法5种指纹库构建方法扩展得到的指纹库，分别用于在线定位阶段时的定位精度。

4.4.1 平均定位误差

为分析各预处理方法对定位误差的影响，实验对比了5种扩充指纹库在WKNN定位算法下的平均定位误差。从图9显示的WKNN算法近邻点数量K与各算法定位误差的关系，可以看到，总体上随着K的增加，5种算法的e都呈下降趋势。其中由于指纹点分布稀疏，无插值方法在K=1时误差极高且下降速率较慢，整体误差高于其他算法0.5 m以上；而DB-RBF和全采法受益于较为精准的指纹信息，下降速率最快。

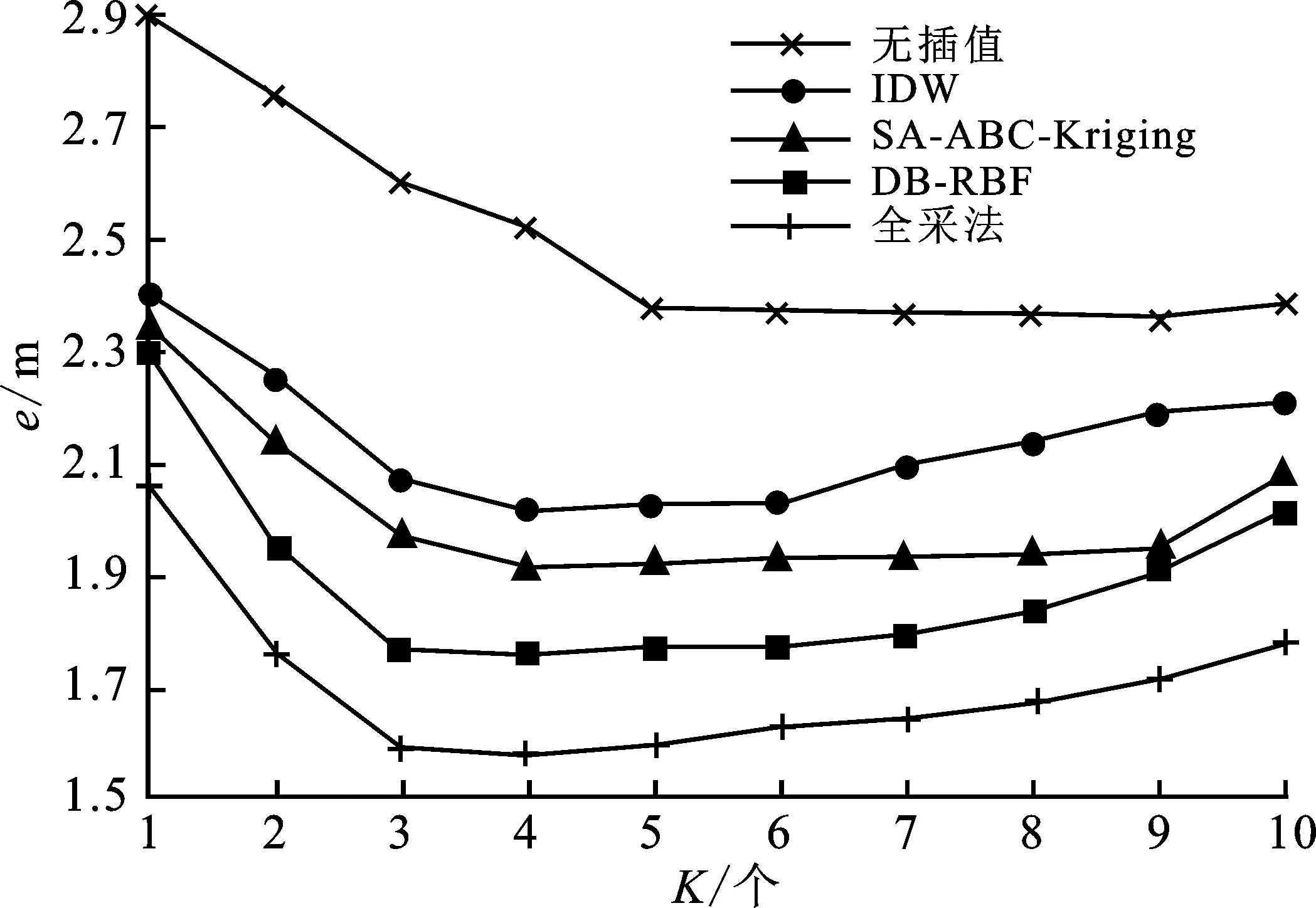
图9 算法的平均定位误差对比

从最优近邻点数量下的平均误差来看，DB-RBF相较于无插值、IDW、SA-ABC-Kriging三者，具有最低的误差值。其中无插值方法定位误差最高，比DB-RBF高出0.61 m；同时DB-RBF的平均误差也比IDW和SA-ABC-Kriging分别降低0.25 m和0.22 m，占比分别约为20.21%和15.38%，可见文中算法具有良好的定位效果。另外，全采法具有最低的平均误差e=1.58 m，低于文中的DB-RBF方法的约10.8%。在牺牲较小定位精度的前提下，DB-RBF做到了扩充1倍以上指纹库容量，且采集比例可根据场景特性调整，具有高度的灵活性。

4.4.2 误差累积概率

给定应用下的emax∈[0，4.2 m]容忍范围内，通过实验可确定各扩充指纹库的测试点定位结果满足e≤emax的概率pe，记为误差累积概率。本实验给出了在不同的emax限制下，上述5种算法的pe对比情况。从图10可以看出，5种算法的pe均随误差容忍范围的扩大而升高，最终达到100%。当给定emax≤0.9 m时，由于允许误差小于一个单位的指纹点间隔距离，因而5种算法的pe相差不大且都较低，此时的误差水平受到指纹点设定影响。而误差容忍范围继续扩大后，DB-RBF的pe曲线表现出仅次于全采法的上升速率。当emax≤3 m时，DB-RBF的pe已经达到约90.4%，可见该场景下DB-RBF的定位误差基本能够控制在3倍指纹点间隔距离以内，具备良好的定位稳定性。

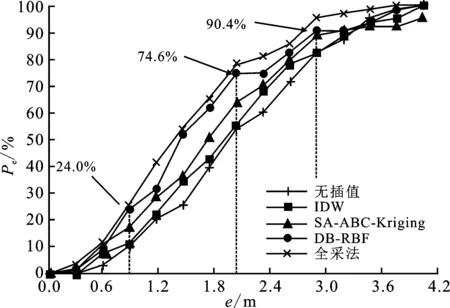
图10 算法的误差累积概率对比

5 结束语

针对室内定位中传统指纹库构建工作繁复，一般扩充方法精度有限且所需信标点较多的问题，笔者提出了基于双信标机制，采用径向基神经网络进行插值的指纹库扩充方法。DB-RBF算法能够依赖少量信标点，插值得到精度较高的指纹信息，同时大幅减少了采集工作量。然而，本着客观的态度，必须看到，对于极少数存在的不规则角落的应用场景，和其他大多数方法一样，DB-RBF也可能存在参考信标不足而预测准度欠佳的遗憾。另外，实验的室内环境未引入动态干扰条件。因此，面向场景死角中的指纹构建和匹配计算问题和动态干扰源条件下的预测稳定性将会是定位研究的重点方向。