基于改进智能霍夫变换的红热圆形工件直径检测
2022-07-04张新雨李思雨李婧华杨延西2
张新雨, 李思雨, 李婧华, 杨延西2,
(1.西安理工大学 晶体生长设备及系统集成国家地方联合工程研究中心, 陕西 西安 710048;2.陕西省复杂系统控制与智能信息处理重点实验室, 陕西 西安 710048;3.西安理工大学 自动化与信息工程学院, 陕西 西安 710048)
直径在现代工业生产中是一个重要的参量,对其进行检测与控制是硅单晶生长、精密工件制造、热锻件生产等领域中的一个重要环节[1-3]。因为直径可以提供产品形状的有用信息,对直径进行检测可以提高识别和控制系统的精度,从而提高产品质量或检测产品是否合格,尤其是在高温环境中,对产品直径进行准确的检测,更有利于提高产品质量、降低修复不合格产品的成本。然而,当工件在高温环境中被加热时,传统的接触式直径测量方法很难直接应用。随着电荷耦合器件(charge coupled device, CCD)的发明,许多基于视觉的直径检测方法被提出[4-6]。这些方法首先用CCD摄像机采集红热圆形工件的图像,然后通过对该图像进行分割和边缘提取,得到红热圆形工件的边缘。由于摄像机拍摄时存在一定的射角,所以红热圆形工件的边缘在图像中是一个椭圆,对这些边缘点进行椭圆拟合,便可得到红热圆形工件的直径。因此,红热圆形工件的直径检测问题实质上是一个椭圆拟合的问题。由于受热辐射的影响,图像中工件的边缘较为模糊,在分割和边缘提取过程中会产生大量的噪声,为椭圆拟合带来了较大的困难。因此,提出一种高精度、强鲁棒的椭圆拟合方法,对提高红热圆形工件直径检测精度具有重要的意义。
目前,常用的椭圆拟合方法主要有三种:最小二乘法(least squares, LS)、随机抽样一致性法(random sample consensus, RANSAC)和霍夫变换(Hough transform, HT)。最小二乘法的基本思想是通过最小化椭圆方程与真实点之间的距离来求椭圆的参数。该方法具有良好的实时性和可实现性,但在数据点中包含大量噪声时鲁棒性较差,检测精度较低。虽然很多学者提出了改进方法,但检测精度仍然受噪声影响较为严重[7-8]。而RANSAC的思想是首先根据边缘点中抽取的一个子集估计椭圆模型,然后去测试子集外的点是否满足此模型,若满足则将该点划分到子集内,重复上述步骤,包含数据点最多的子集对应的椭圆模型就是最优的模型[9]。与最小二乘法相比,RANSAC鲁棒性更强,但RANSAC的检测精度受迭代次数限制,当迭代次数设置不合理时,椭圆参数误差较大。霍夫变换主要利用投票法则在参数空间中寻找椭圆参数的最优值。该方法鲁棒性强、精度高,但它由于采用了穷举的方法,实时性较差、占用内存过多,难以满足大多数工业检测中的需求[10-11]。为克服霍夫变换的缺点,许多学者提出了改进方法。Xu等将解方程的步骤引入了霍夫变换,提出了随机霍夫变换(randomized Hough transform, RHT),大大减少了计算量,被广泛应用于人脸检测等领域[12-14]。随机霍夫变换虽然减少了霍夫变换的计算量和内存占用存储量,但由于解方程步骤的引入,鲁棒性被破坏。根据霍夫变换的原理可知,霍夫变换的实质就是一个最大化的优化问题,即在参数空间中搜索数据点投票数最大的一组椭圆参数。近年来,随着模拟退火(simulated annealing, SA)等智能优化方法的提出和完善,为改进霍夫变换提供了一种新的思路[15]。模拟退火算法具有较好的全局搜索能力,运行效率高且易于实现。
因此,本文提出了一种基于模拟退火算法的改进智能霍夫变换方法,以提高霍夫变换检测红热圆形工件直径的速度和精度。首先,根据霍夫变换的原理设计了目标函数。其次,提出了混合Metropolis Hastings (MH)抽样方法。再次,基于该抽样方法利用模拟退火算法在参数空间中搜索最优椭圆参数,从而获得红热工件的直径测量值。最后利用标准椭圆和红热圆形工件实际图像对本文所提方法进行了有效性验证。
1 问题描述
由于红热圆形工件温度较高,对其直径进行直接检测较为困难,所以基于CCD摄像机的非接触直径检测方法被广泛应用。该方法原理见图1,在工件上方安装一部CCD摄像机,利用该摄像机采集红热圆形工件的图像,然后对该图像进行分割和边缘检测就可得到工件轮廓边缘点。
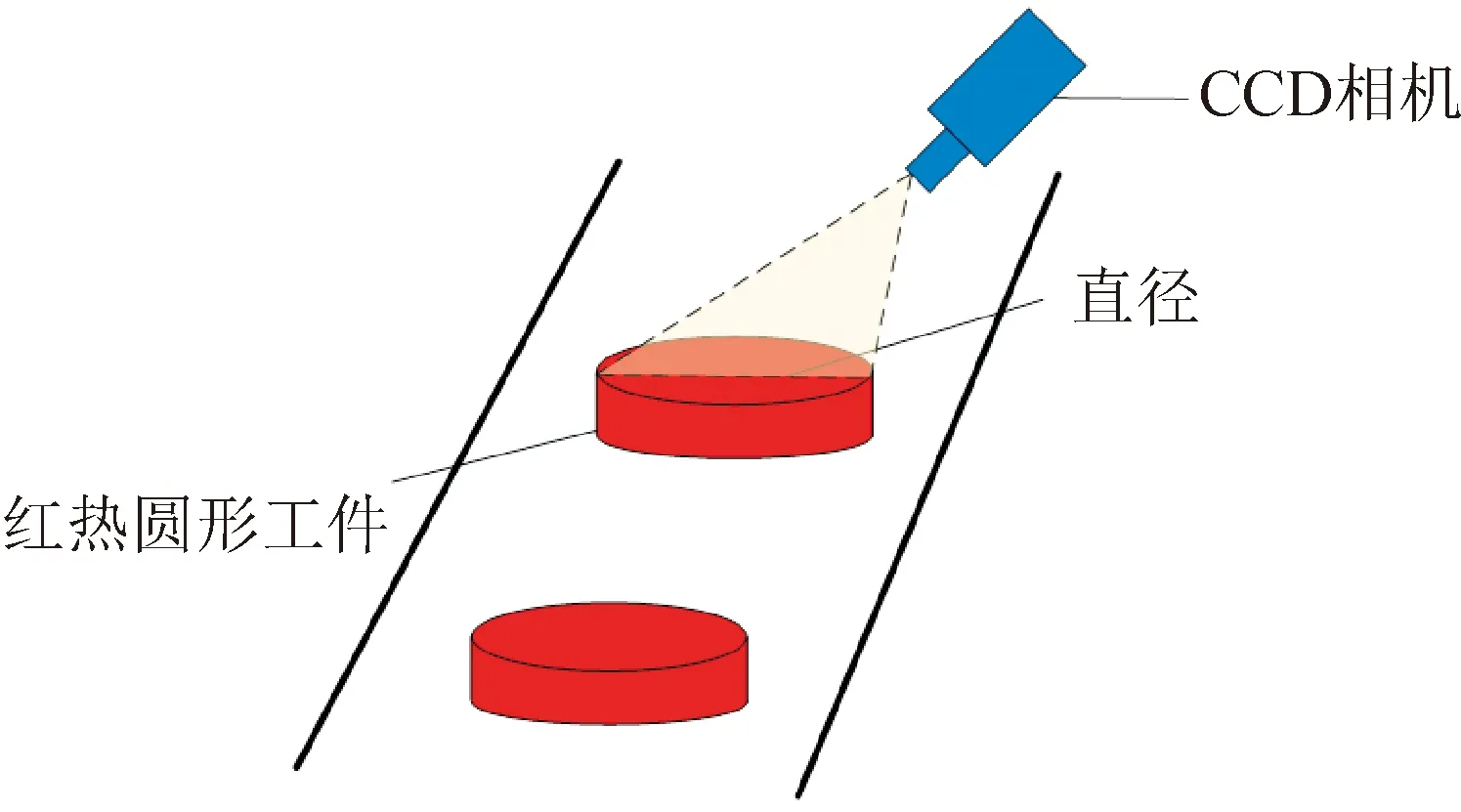
图1 基于CCD摄像机的红热圆形工件直径检测原理Fig.1 Diameter detection principle of red hot circular workpiece based on CCD camera
由于CCD摄像机安装时存在一定的角度,工件的轮廓在图像中形成一个椭圆。对工件轮廓边缘点进行椭圆拟合,就可以检测出红热圆形工件的直径。因此,如何对椭圆进行高精度拟合,就成为检测红热工件直径的一个关键问题了。
设红热工件轮廓的边缘点集为(xm,ym),其中m=1,2,...L,L是点的个数。由这些点构成的椭圆方程为:
(1)
式中:a和b分别是椭圆的长半轴和短半轴;(xc,yc)是椭圆中心的坐标。
由于CCD相机拍摄时存在一定的角度,成像过程中红热圆形工件的形状在垂直方向上发生了变化,但水平方向没有变化,最终在图像中变为椭圆。根据上述检测原理可得,红热工件直径即为椭圆的长轴2a,所以当得到椭圆最优参数时就可以得到红热工件的直径。然后由于热辐射等因素的影响,边缘点中存在大量的噪声,难以得到精确的椭圆参数。虽然霍夫变换具有较好的鲁棒性和精度,但由于其使用穷举的方法,算法复杂度和内存占用量较大,在许多工业环境中难以实现。因此,如何对霍夫变换进行改进,在保持其鲁棒性强和精度高优点的基础上降低它的算法复杂度和内存占有量,成为实现对红热圆形工件直径快速、精确检测的关键问题了。
2 基于模拟退火算法的改进智能霍夫变换
2.1 模拟退火算法
1953年,Metropolis等[16]提出了模拟退火算法。1983年,Kirkpatrick等[17]成功地将模拟退火算法应用于组合优化领域中。其核心思想与热力学的原理相似,温度高时由于固体内部分子具有较高的能量,所以排列呈无序状态。随着温度缓慢下降,固体内部分子将在每个温度都达到平衡态,最终在常温时达到基态,此时内能最小[18]。内能E可看作优化目标,分子状态x可看作可行解。模拟退火算法通过使用Metropolis准则,即粒子在温度T时趋于平衡的概率为exp(-ΔE/T),其中E为温度T时的内能,ΔE为其改变量。标准模拟退火算法的流程见如下所述。
1) 初始化。设置初始温度T,初始状态解x0,每个温度值下的迭代次数L,温度下降率ε,并设置E(x)为目标函数,令k=1。
2) 产生新解x′,计算内能增量ΔE=E(x′)-
E(x)。
3) 若ΔE<0,则接受x′作为新的当前解,否则依据概率exp(-ΔE/T)接受或拒绝新解x′。
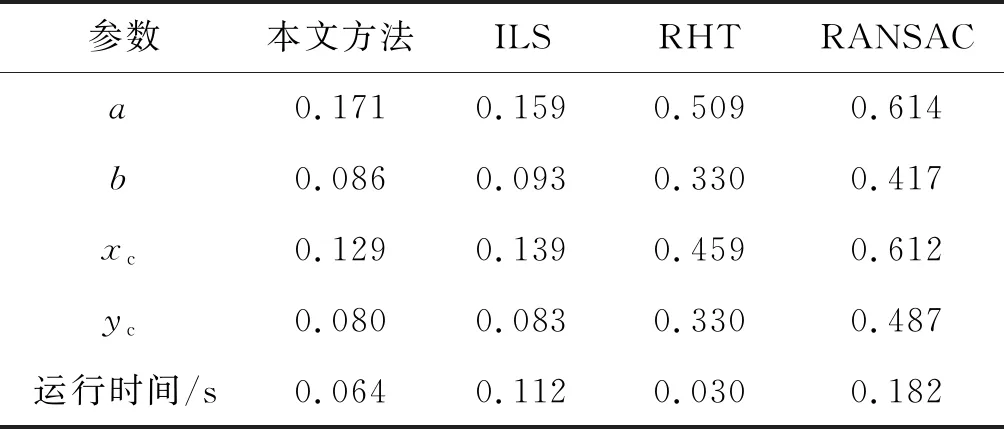
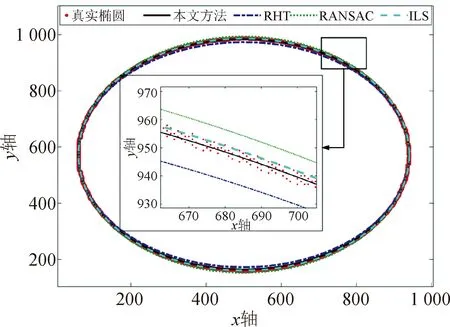
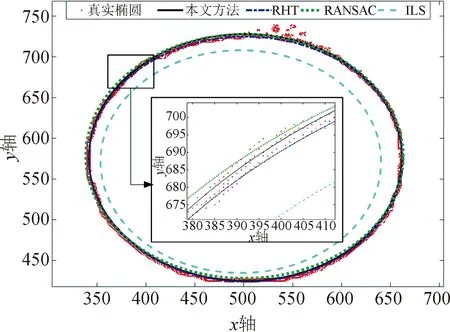
4)k=k+1,若k 5) 根据温度下降率ε让T逐步减小,如果温度小于最低温度,则程序终止,将当前状态作为最优状态输出,否则令k=1,转到步骤2)。 霍夫变换拟合椭圆的一般思想是将椭圆方程映射到参数空间,将参数空间中的(xm,ym)看作常量,(a,b,xc,yc)看作未知参数,通过利用穷举的方法遍历参数空间中的每组(a,b,xc,yc),然后将其代入式(4)中,如果满足条件,就在参数累加器中加1。参数空间中每组数据都列举完成后,累加器中最大值对应的参数(a,b,xc,yc)就是最优的椭圆参数。 从霍夫变换的基本原理可以看出,使用穷举的方法具有两个严重的缺点,即较高的算法复杂度和较大的内存需求量。这两个缺点使霍夫变换无法满足在大多数实际应用中的实时性要求。然而,霍夫变换的本质是搜索使累加器达到最大值的参数优化问题。模拟退火是一种经典的优化算法,具有较强的全局搜索能力。根据霍夫变换原理,并考虑噪声的影响,本文设计模拟退火算法的目标函数为: (2) (3) (4) 式中:f(a,b,xc,yc,xm)表示(a,b,xc,yc)的累加器;Tf为阈值,用以提高智能霍夫变换的鲁棒性。当f(a,b,xc,yc)最小时,对应的(a,b,xc,yc)即为最优的椭圆参数。随着目标函数的构造,霍夫变换拟合椭圆的问题已转化为一个优化问题,利用优化算法可以提高霍夫变换的实时性,并可以降低霍夫变换的内存需求量,同时可以很好的保持霍夫变换的鲁棒性和精度。 基于模拟退火算法的改进智能霍夫变换检测椭圆的步骤为如下所述。 2) 根据先验知识在四个均匀分布的区间内抽取随机数作为初始椭圆参数,代入目标函数f中。 4) 将新解a代入式(2)~(4)中计算f′,若f′小于当前f,则接受新解a并代替当前解,f′代替当前f值,反之则拒绝。 5) 按照步骤3)中所述依次对参数b,xc,yc进行抽样后接受或拒绝。 6)k=k+1,若k 7) 判断温度Ti是否达到温度下限Tmin,达到则结束程序,否则转步骤8)。 8) 根据式(5)计算新的温度Ti+1,然后令k=1,转步骤3)。 Ti+1=εTi (5) 为验证本文方法的有效性,设计了两个实验,并与ILS、RANSAC和RHT方法进行对比。第一个实验是仿真,利用包含高斯噪声的完整椭圆进行验证,第二个是通过将圆形垫片加热到红热状态进行验证。 图2 100个带有噪声的椭圆数据点Fig.2 100 ellipse data points with noise 图3为四种方法拟合椭圆的结果。从图3可以看出,本文方法在包含噪声的椭圆拟合方面优于其它三种方法。 图3 不同方法的拟合结果Fig.3 Fitting results by different methods 为对实验结果进行客观评价,本文选用了均方根误差(root mean square error,RMSE)作为评价指标,RMSE的定义如下: (6) 表1为在100次独立实验中本文方法与ILS、RANSAC、RHT的RMSE及运行时间。由表1可得,由于本文所提方法将霍夫变换转换为全局优化问题,并使用模拟退火算法搜索霍夫变换累加器对应的参数最优值,因此具有较高的准确性和搜索效率,并且与RANSAC和ILS相比大大减少了运行时间,提高了霍夫变换的运行效率。 表1 不同方法的检测结果Tab.1 Test results by different methods 为验证本文方法在实际工程中检测红热圆形工件直径的有效性,本实验用红热状态的圆形垫片进行验证。红热圆形垫片的图片见图4。由图4可得,该垫片由两个椭圆组成,分别是外椭圆和内椭圆。因此,在本节中设计了两个实验,一个是检测外椭圆的直径,通过内椭圆标定的真实值进行验证;另一个是检测内椭圆的直径,通过外椭圆的真实值进行验证。 图4 红热圆形垫片图像Fig.4 Red hot circular gasket image 通过对该图像进行阈值分割和边缘检测可以得到外椭圆的5 342个采样点和内椭圆的2 025个采样点。然后由本文方法,ILS、RHT和RANSAC拟合椭圆后得到外椭圆和内椭圆的直径,最后比较了四种方法的结果。 1) 红热圆形工件的外径检测实验 图5为四种方法对红热垫片外椭圆的检测结果,由图5可以看出,与RHT和RANSAC相比,本文方法与ILS拟合的结果更接近真实椭圆。 图5 不同方法对红热垫片外椭圆的拟合结果Fig.5 Fitting results of outer ellipse of red hot gasket by different methods 表2为在100次独立实验中本文方法与ILS、RHT、RANSAC的RMSE及运行时间。由表2可得,与ILS、RHT和RANSAC相比,本文所提方法大大提升了准确性和运行速度。 2) 红热圆形工件的内径检测实验 图6为四种方法对红热垫片内椭圆的检测结果,由于图像上方存在噪点,对ILS的拟合结果影响较大。从图6可以看出,与ILS、RHT和RANSAC相比,本文方法拟合的结果准确性更高。 图6 不同方法对红热垫片内椭圆的拟合结果Fig.6 Fitting results of inner ellipse of red hot gasket by different methods 表3为在100次独立实验中本文方法与ILS、RHT、RANSAC的RMSE及运行时间。从表3可以看出,与ILS、RHT和RANSAC相比,本文算法运行时间最短,准确性最高,大大提高了霍夫变换的运行速度。 表3 不同方法对红热圆形工件内径的检测结果Tab.3 Test results of inner diameter of red hot circular workpiece by different methods 为降低霍夫变换的算法复杂度和内存空间占有量,本文提出了一种基于模拟退火算法的改进智能霍夫变换方法。根据霍夫变换检测红热圆形工件的问题设计了目标函数,并设计了Gibbs和MH混合抽样策略,改进了模拟退火算法,最后利用模拟退火算法在霍夫变换的参数空间中搜索椭圆参数的最优值。与ILS、RHT和RANSAC相比,本文方法对标准椭圆和红热圆形工件内外边缘都具有较好的检测结果。不仅保持了霍夫变换的高精度和强鲁棒性优点,还显著地提高了霍夫变换的运行速度,降低了霍夫变换的内存占有量,对于高温环境中圆形工件生产时的直径检测具有重大意义。2.2 改进智能霍夫变换的目标函数
2.3 抽样算法设计
2.4 改进智能霍夫变换的算法步骤
3 实验结果及分析
3.1 仿真
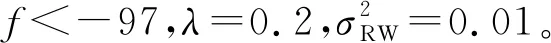
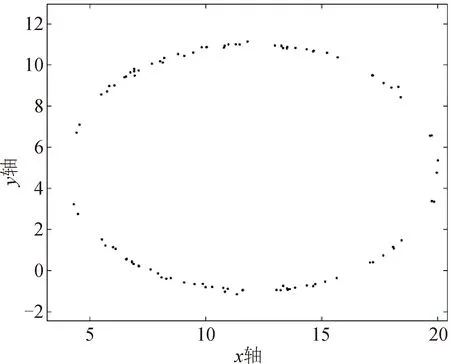
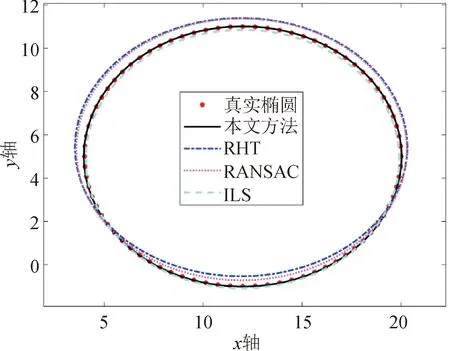
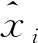
3.2 红热圆形垫片的直径检测实验

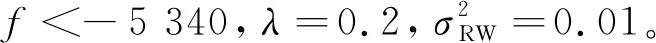


4 结 语
