基于遗传算法和灰色神经网络的电力机车产品需求预测方法
2022-07-04魏巍贺雷永李垂辉
魏巍,贺雷永,李垂辉
基于遗传算法和灰色神经网络的电力机车产品需求预测方法
魏巍1,贺雷永1,李垂辉2
(1.北京航空航天大学 机械工程及自动化学院,北京 100191;2.襄阳博亚精工装备股份有限公司,湖北 襄阳 441004)
应对快速多变的市场,提前预知市场发展,制定相应的排产计划,使企业在竞争中占据先发优势。目前基于灰色神经网络的预测算法,准确地预测产品需求通常需要连续且大量的样本数据,对小数据非线性系统的预测结果精确度低、可靠性差,针对这一问题,提出一种耦合遗传算法的灰色神经网络预测方法,综合灰色模型和神经网络理论,构建了面向产品订单量需求预测的灰色神经网络模型;通过电力机车产品实例分析了模型的预测性能;为解决预测过程中模型早熟收敛的问题,利用遗传算法对训练网络的权重和阈值进行了迭代优化。研究结果表明,优化后产品预测模型的精确性和鲁棒性得到提高,验证了所设计方法的可行性。
需求预测;灰色模型;神经网络;遗传算法
信息技术的快速发展促使大规模定制从落后的库存导向型生产模式向订单导向型生产模式转变,从而提高效率,降低库存,并提升整体的生产力水平。产品需求预测是大规模定制产品的出发点,是企业分析其产品在一定时间内需求期望水平的重要途径。提前预知客户需求可以为企业的生产计划和控制决策提供依据,有效提升客户满意度,让企业在竞争中占据有利地位。随着市场的快速发展,定制化生产模式下的客户需求往往是动态的、多方面的、不确定的,极少的用户具备对自我需求信息的精确描述能力, 并且用户之间还存在很大的个体差异[1]。也就是说用户需求趋向多样化和个性化,致使准确预测产品需求愈发困难,因此,寻找更加有效的预测手段对企业发展显得十分迫切。
机车作为铁路运输的物质基础,仍然存在着生产不合理的情况,导致闲置、不足、效率低下等问题,造成这一切的原因,是缺乏科学的需求预测方法。郭依超等[2]从市场需求、牵引需要等角度出发,完成双动力源机车的市场前景分析。杨畅[3]运用线性回归法、灰色预测法组合预测,通过对机车历史保有量、设备更新改造的分析,预测未来铁路机车总拥有量。神经网络(Neural Network, NN)具有很强的记忆能力和自适应能力,并且可以映射任何非线性系统,因此作为一种出色的非线性工具,近年来,它在各种模拟和预测领域中得到了广泛的应用[4]。NN本质上受收敛速度慢和局部最小值限制,需要大量的样本数据参与训练,并且对未知数据的适应能力有限。通常需要采用反复试验的方式对NN模型进行设计和结构上的优化,效率比较低下[5]。为了解决这些问题,许多研究人员使用模型组合方法来改进和优化神经网络。其中包括,使用灰色系统理论处理数据量少的限制,以提高神经网络模型的预测精度,这种模型称为“灰色神经网络”。当使用遗传算法(Genetic Algorithm, GA)时,可以通过搜索全局最优解,优化NN的网络体系结构和连接权重[6]。Yang等[7]针对中国石油消费历史数据量小的问题,提出一种基于灰色理论、神经网络和遗传算法的改进混合算法GGNN用于预测中国长期石油消费需求。张彦粉等[8]通过研究遗传算法优化BP神经网络建立自变量与因变量之间的关系,对可食用油墨的黏度进行了预测和模拟。李永锋等[9]提出基于灰色系统理论的产品意象造型设计方法,通过灰色预测建立产品感性意象的预测模型,并对模型的有效性进行分析,在电热水壶的造型设计上应用验证。刘巍等[10]通过将等式约束处理为不等式约束与改进交叉算子和变异算子,提高了遗传算法的收敛速度,其构建的多元灰色神经网络模型预测性能优于单一模型,而且适用于目标函数为不可微函数的情况。
以上对灰色神经网络预测模型的应用与优化改进研究,通常使用的样本连续且数据来源充足,然而,现代市场中,企业定制产品具备的样本数据呈非线性且较为匮乏。针对小数据不确定系统的预测问题,文中提出一种耦合遗传算法的灰色神经网络预测方法。以某企业电力机车历史订单数据为样本,首先构建灰色神经网络模型,进行未来需求预测,然后,采用遗传算法优化选取网络的最佳初始权阈值,解决模型早熟收敛问题,最后通过电力机车产品实例对结果进行对比分析,以实现提高预测准确性和鲁棒性的目的。
1 灰色模型与NN预测模型
1.1 灰色系统理论模型
灰色系统理论方法是在短时间序列内以有限的时间范围进行建模和预测的有效方法。灰色系统理论模型简称GM模型,在水文学[11]、控制系统[12]、技术系统分析[13]、磨损过程描述[14]等领域具有广泛的应用。这些领域的许多研究与基于少量数据的预测有关。通过对系统中原始数据的灰色建模、挖掘和整理,揭示给定数据序列的固有规律性,进而实现对未来数据发展情况的预测[15]。与传统方法相比,灰色预测分析所需的数据量较少,运算方便,且预测结果的精度较高[16]。
GM(1,1)模型是通过累加操作使其呈现出一定的规律性,再对生成序列进行白化微分方程处理生成的。GM(1,1)模型的建立步骤如下。


3)构造GM(1,1)灰色微分方程:
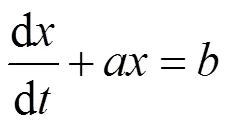
用最小平方法求解参数和。
累减获得灰色预测模型和预测值。
1.2 NN预测模型
NN是由大量处理单元广泛互连的网络,其拓扑结构见图1。反馈神经网络将接收层添加到前馈网络的隐含层中,将隐含层的输出反馈到接收层,然后在接收层延迟一步后输出到隐含层,因此具备了解决非线性问题的能力。系统具有联想存储的功能,并且可以直接反映系统动态过程的特性。多层前馈感知器网络增强了分类和识别能力,但同时样本的训练时间与模型的学习时间也相应加长。
神经网络的工作原理:信息通过输入层进入网络,信息在层与层之间进行梯度下降传递。样本信息在网络中有2个流向,一是输入信息和网络权重的前馈传播,直到输出层输出,即工作信息流向;二是实际输出未达到期望输出时,误差的反方传播,并对网络进行迭代更新,直到误差小于阈值,即误差信息流向。

图1 NN三层拓扑结构
NN预测模型的流程见图2,首先初始化网络参数,以防神经网络出现局部极小的情况,再输入训练样本数据进行模型训练,当输出误差大于期望误差时,对网络权重进行迭代修正,直到达到期望值要求,得到训练好的预测模型。具体步骤如下。
1)初始化权值、阈值,输入学习速度和期望误差;根据输入样本,确定输入输出序列和各层节点数。
2)计算隐含层和输出层各神经元的输出。
3)计算误差,包括期望与训练输出的偏差、平方和误差、输出层各神经元的输出误差、隐含层输出误差。
4)修正神经网络权重。

图2 NN预测模型流程
2 灰色神经网络预测模型
2.1 灰色神经网络理论
虽然灰色预测模型能够通过不完全信息对不确定系统的发展进行预测,但仍存在以下2点不足。
1)灰色预测模型只能进行短期预测,当时间跨度变长后,灰色系统已知信息的贫瘠性缺点开始显露,系统受到的噪声干扰无法排除,因此,灰色预测模型在进行中长期预测时精度不足。
2)灰色预测模型缺乏自学习功能,在预测过程中没有误差反馈机制,因此无法对模型本身进行迭代修正,导致适应性不足。
相较于灰色预测模型,NN预测模型拥有自学习能力,通过误差反向传播对网络参数进行迭代修正,能够得到比较准确的预测结果。但也存在有以下不足。
1)为了获得有效的模型,NN需要大量的样本数据参与训练,否则网络无法保证精度。
2)NN是一种梯度下降求解机制,在求解过程中易陷入局部最优,导致全局求解能力差。
灰色预测模型和神经网络预测模型在各自的领域都已经是成熟并且应用广泛的预测方法,为了扩大适用范围,尤其针对电力机车这种复杂定制装备的订单预测问题,很难提供大量的精确信息样本。因此将灰色系统和神经网络进行结合,以发挥各自的优点,实现对小数据不确定系统的预测,具有非常现实的意义。
2.2 灰色神经网络预测模型
将GM的预测结果输入到NN对模型进行非线性拟合,利用误差逆向传播算法优化网络权值和阈值,实现对信息数据量欠缺事件的准确预测[17]。

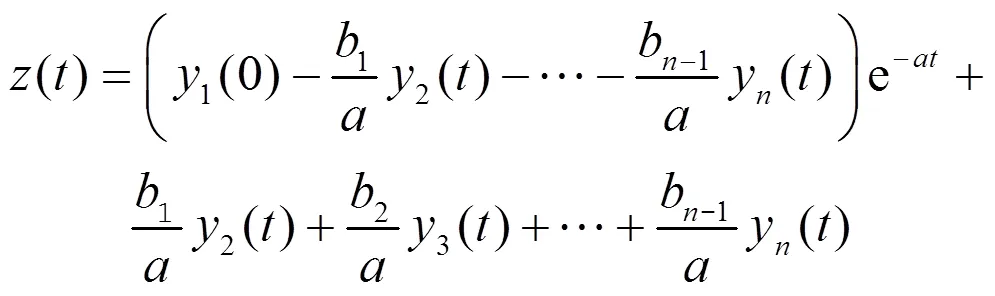
进行参数替换:

对式(5)进行转化:
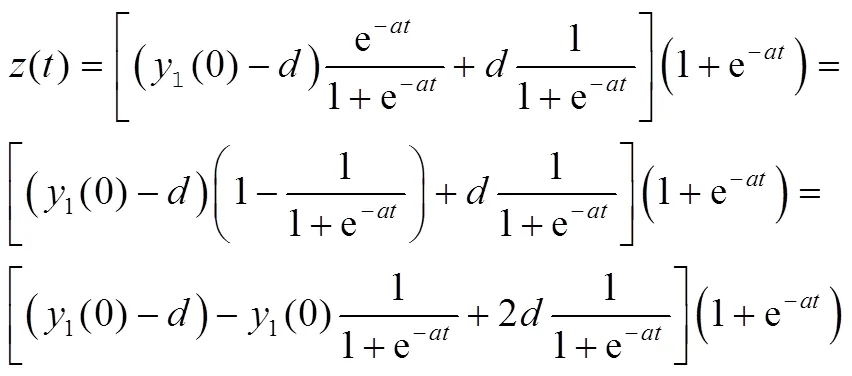
将其映射到扩展的NN中得到GM-NN模型,其拓扑结构见图3。
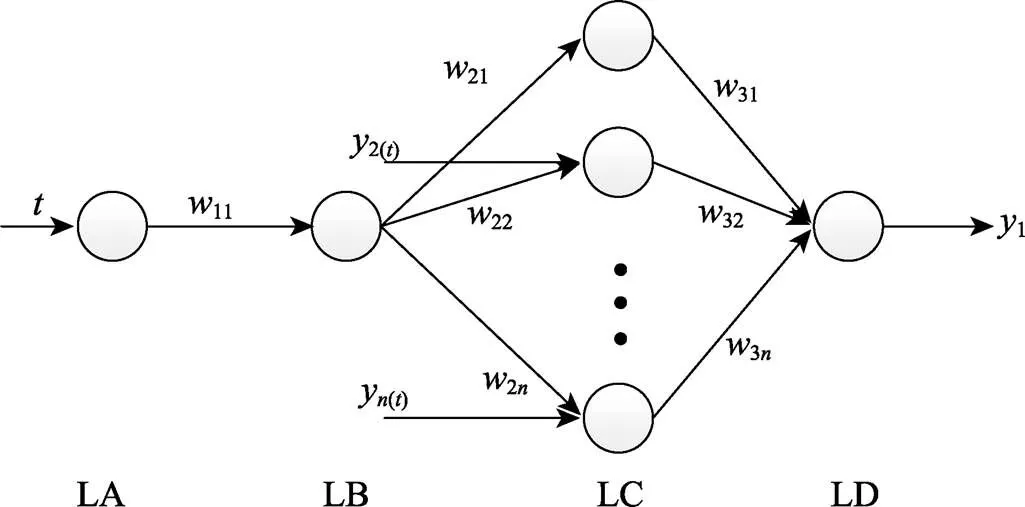
图3 GM–NN拓扑结构
GM–NN模型的学习步骤如下。
初始化网络参数,根据样本数据设定,的初始值,并计算出计算网络权重和输出阈值。
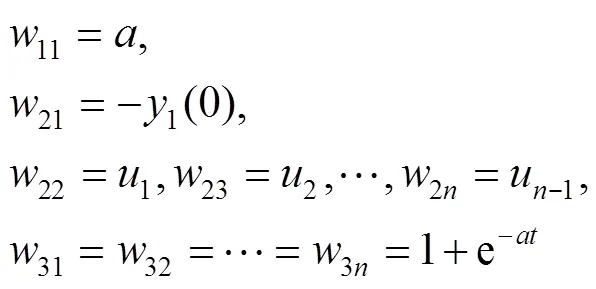
其中:
LD层:

LA层:

LB层:

LC层:

LD层:
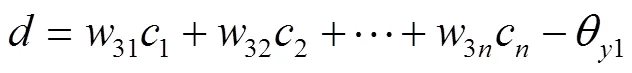
反向传播计算各层的误差:
LD层误差:

LC层误差:

LB层误差:
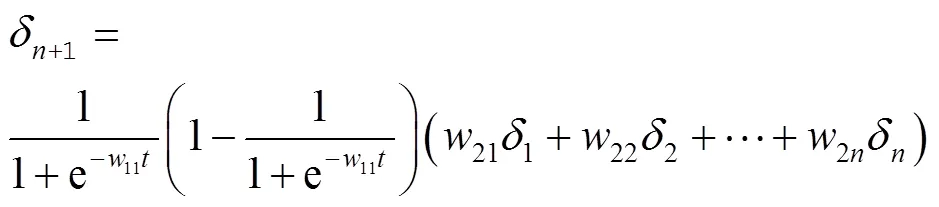
根据误差修正权重和阈值
调整LB层到LC层的权重:

调整LA层到LB层的权重:

调整阈值:
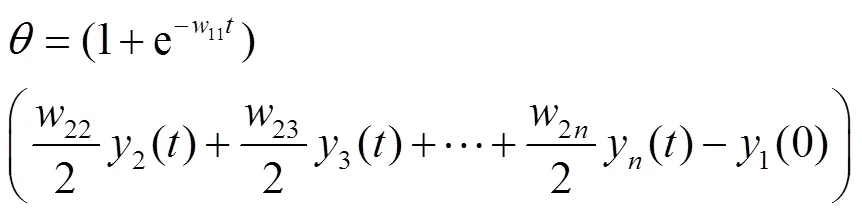
判断是否满足误差要求,未满足则返回步骤,执行迭代训练。
灰色神经网络预测模型的流程见图4,首先构建合适的灰色神经网络,然后,初始化网络后在约束条件内对网络进行迭代训练,最后,利用成熟的模型对输入数据进行预测。
2.3 电力机车产品订单需求预测
电力机车即电力火车,是从供电网或供电轨中获得电能,通过电动机驱动车辆的火车,主要由车体、转向架、车钩及缓冲、主电路、机车电气线路、变压器、牵引电机、控制系统、辅助系统等部分组成,又分为客车、货车等多种形式。为适应不同工作环境,电力机车产品型号众多,虽然功能类似,但是产品的结构尺寸与提升高度差异较大,是高度定制化的产品,关于需求预测的数据相对匮乏,是典型的小数据非线性不确定系统预测问题。
2.3.1 需求预测对象
根据某企业已有的电力机车历史需求信息库建立灰色神经网络预测模型,预测未来该型号电力机车每季度的订单需求数量,从而指导企业进行产品设计生产的决策和规划。
2.3.2 电力机车市场需求影响因素
机车凭借其出色的运载能力,较高的可靠性、安全性、稳定性,在生活、建设中发挥着不可替代的作用,市场需求巨大。影响其订单需求的因素很多,包括但不限于产品质量、品牌认可度、价格波动、性价比、环保能级等。某企业提供的电力机车订单需求影响因素如下。

图4 GM–NN预测模型流程
1)市场份额。市场份额指企业某产品的销量在市场同类产品中所占比重。
2)品牌认可度。品牌认可度指客户对某一种品牌的熟悉和忠诚程度,在面对同类产品时,客户由于对某品牌产生的深刻印象和吸引力,导致会优先购买该品牌产品,购买次数明显高于其他品牌。
3)价格波动。价格波动指企业为了达成某一目的,主观造成的市场短期价格变化。价格波动也会导致短期内产品需求的突然波动。
4)订单满足率。订单满足率指由于产能不足、原材料紧缺、排产延误等原因导致的不能满足客户原定产品数量订单占全部订单的比重。
5)售后服务满意度。售后服务满意度是客户对企业服务的主观层次评价。售后服务满意度直接反映了客户的心理状态和体验感受。
2.3.3 预测结果分析
以2012—2017年共计6年24个季度的某企业电力机车订单作为验证实例,训练样本为前18个季度的订单量数据,后6个季度订单量作为测试模型预测性能的试验数据。样本数据源自某企业提供的历史销售数据。对原始数据进行归一化去量纲处理作为预测模型的输入/输出矩阵,为24行6列矩阵,第1列为电力机车订单量,2至6列分别为市场份额、品牌认可度、价格波动、订单满足率和售后服务满意度,见表1。
在Matlab软件平台中迭代训练网络模型。以前18个季度的订单需求数据作为训练样本,后6个季度的需求数据作为对比数据,GM–NN预测模型的输出结果见图5。
由图5a可知,模型的收敛速度很快,进化次数呈断崖式下降,迅速进入成熟期,实现预测功能。同时,模型暴露出的早熟收敛问题导致神经网络过早地完成进化,无法对网络参数值进行迭代修正,极易陷入局部最优,无法跳出,严重影响了预测精度。用训练好的GM–NN预测模型对电力机车产品历史订单进行预测,取20次预测结果的平均值绘制订单量预测曲线,结果见图5b,预测曲线与实际订单量曲线吻合度较低,个别数据的预测与实际值差距较大,鲁棒性差。取20次预测结果的平均值通过与实际订单数据进行比较分析,计算相对误差,结果数据见表2,预测结果与实际结果的误差存在一定波动,预测的平均误差为4.59%。
表1 电力机车历史订单数据

Tab.1 Electric locomotive historical order data
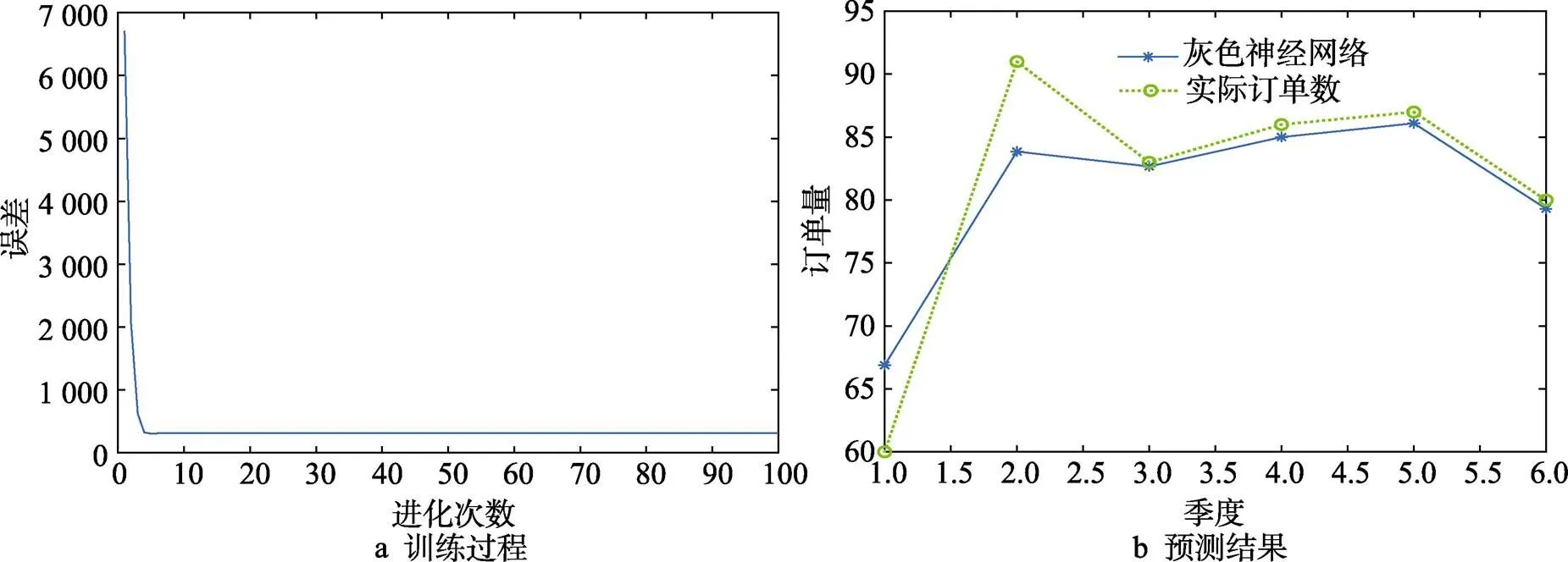
图5 GM–NN预测结果
表2 GM–NN预测结果分析

Tab.2 GM-NN prediction result analysis
3 GA–NN预测模型
尽管GM–NN预测模型能够快速收敛并预测未来需求,但是它仍然存在许多缺陷。例如,鲁棒性很差,并且网络性能对网络的初始权重设置非常敏感。NN很容易陷入局部最小值,无法获得全局最优解,因此此次研究使用遗传算法优化NN模型的权重和阈值,然后构建GA–NN预测模型,GA–NN优化流程见6。
遗传算法(Genetic Algorithm,GA)是一种通过模拟具有良好全局特征的生物遗传和进化过程而建立的全局优化算法[18]。它可以用来优化NN,使其具有自我进化功能,从而构建具有全局搜索能力的NN。具体过程为,使用GA算法的全局搜索功能来查找与网络初始次优解相对应的权重和阈值,并将其用作网络的初始权阈值。使用NN算法对网络进行训练,可以很好地防止网络陷入局部极小值,提高收敛速度,摆脱对初始值的依赖。步骤如下:
1)确定GA–NN的初始结构和参数。输入样本数据,设置最大进化代数和网络节点的初始权阈值。
2)确定GA操作,设置参数和编码。对灰色神经网络的网络参数,即初始权重和阈值进行实数编码。
3)设定适应度函数。将灰色神经网络的预测输出与实际结果的误差函数作为适应度函数。

图6 GA–NN优化流程
4)将获取到的最优网络参数结果输入灰色神经网络层,重新赋值灰色神经网络预测模型的网络参数,然后使用神经网络算法对网络进行训练,最后得到成熟的预测模型进行需求预测。
5)输出最终结果。
4 优化效果检验
为检验遗传算法对灰色神经网络预测模型的优化效果,以3.3节的电力机车需求预测实例进行对比验证,生成适应度曲线和预测结果见图7。
图7a为模型训练的适应度曲线,可以看出,采用遗传算法优化后,模型的迭代学习次数显著增加,多次跳出局部最优,减少了模型早熟收敛的可能性,提高预测准确度;图7b为20次预测结果的平均值绘制的订单量预测曲线,可以看出,GA–GM–NN的预测曲线与实际订单量曲线的符合度优于GM–NN的预测曲线,表明遗传算法优化有效。取20次运行结果的平均值与实际订单数量进行比较,计算模型误差,2种预测模型的预测误差见表3。

图7 GA–GM–NN预测结果
由预测结果对比可知,灰色神经网络预测模型的预测结果平均误差为3.62%,经遗传算法优化后平均误差降到了3.03%,证明优化有效。由此可知,通过遗传算法选择网络最优权阈值,可有效改善灰色神经网络预测模型的可靠性和鲁棒性,提高预测性能。
表3 预测结果对比

Tab.3 Comparison of prediction results
5 结语
文中构建了一种基于遗传算法的灰色神经网络预测方法,实现了预测小数据不确定系统的目标。该方法具有以下优点。
1)用于预测产品订单需求的历史数据有限,利用灰色系统理论来处理这一限制。
2)NN具有自适应性,可以逼近任何非线性系统,与GM模型相结合有效提高预测性能。
3)由于神经网络参数不当会导致预测模型早熟收敛和结果多变的问题,因此采用遗传算法来优化网络权重和阈值,防止网络陷入局部极小值,提高收敛速度,摆脱对初始值的依赖,提高预测精度。
最后通过电力机车产品订单实例对结果进行了对比分析,优化后的模型预测性能得到显著提升,证明优化预测模型的有效性,为企业定制产品的需求预测提供了有用参考,有利于制造企业进行合理生产规划,实现资源的最大化利用。
[1] 曹国忠, 石开, 王听. 基于多维感性的用户需求分析方法研究[J]. 包装工程, 2019, 40(6): 119-127.
CAO Guo-zhong, SHI Kai, WANG Ting. User-Requirement Analysis Method Based on Multi-Dimensional Sensibility[J]. Packaging Engineering, 2019, 40(6): 119-127.
[2] 郭依超, 李廉枫, 邓伯勇. 内燃-电力双动力源机车在我国的市场前景分析[J]. 技术与市场, 2016, 23(1): 99-100.
GUO Yi-chao, LI Lian-feng, DENG B Y. Market Prospect Analysis of Diesel-Electric Locomotive in China[J]. Technology and Market, 2016, 23(1): 99-100.
[3] 杨畅. 铁路机车车辆需求预测模型的研究[D]. 北京: 北京交通大学, 2014.
YANG Chang. The Demand Forecasting Model Study of the Railway Locomotives[D]. Beijing: Beijing Jiaotong University, 2014.
[4] SINGHAL D, SWARUP K S. Electricity Price Forecasting Using Artificial Neural Networks[J]. International Journal of Electrical Power & Energy Systems, 2011, 33(3): 550-555.
[5] SHI Xiao-feng. Tourism Culture and Demand Forecasting Based on BP Neural Network Mining Algorithms[J]. Personal and Ubiquitous Computing, 2020, 24(2): 299-308.
[6] XU Tong-le, WANG Ying-bo, CHEN Kang. Tailings Saturation Line Prediction Based on Genetic Algorithm and BP Neural Network[J]. Journal of Intelligent & Fuzzy Systems, 2016, 30(4): 1947-1955.
[7] YANG Yi, CHEN Yan-hua, SHI Jun, et al. An Improved Grey Neural Network Forecasting Method Based on Genetic Algorithm for Oil Consumption of China[J]. Journal of Renewable and Sustainable Energy, 2016, 8(2): 024104.
[8] 张彦粉, 魏华, 葛纪者, 等. 基于遗传算法优化BP神经网络的可食用油墨粘度的预测[J]. 包装工程, 2021, 42(19): 49-54.
ZHANG Yan-fen, WEI Hua, GE Ji-zhe, et al. Prediction of the Viscosity of Edible Ink Based on BP Neural Network Optimized with Genetic Algorithm[J]. Packaging Engineering, 2021, 42(19): 49-54.
[9] 李永锋, 邢艳芳, 朱丽萍. 基于灰色系统理论的产品意象造型设计研究[J]. 包装工程, 2010, 31(14): 43-46.
LI Yong-feng, XING Yan-fang, ZHU Li-ping. Research on Form Design of Product Image Based on Grey System Theory[J]. Packaging Engineering, 2010, 31(14): 43-46.
[10] 刘巍, 李锰, 李秋燕, 等. 基于改进遗传算法的电网投资组合预测方法[J]. 电力系统保护与控制, 2020, 48(8): 78-85.
LIU Wei, LI Meng, LI Qiu-yan, et al. Power Grid Portfolio Forecasting Method Based on an Improved Genetic Algorithm[J]. Power System Protection and Control, 2020, 48(8): 78-85.
[11] TRIVEDI H V, SINGH J K. Application of Grey System Theory in the Development of a Runoff Prediction Model[J]. Biosystems Engineering, 2005, 92(4): 521-526.
[12] DENG Ju-long. Control Problems of Grey Systems[J]. Systems & Control Letters, 1982, 1(5): 288-294.
[13] GUO Ren-kuan. Repairable System Modeling via Grey Differential Equations[J]. Journal of Grey System, 2005, 8(1): 69-91.
[14] ZHANG Hong, LI Zhu-guo, CHEN Zhao-neng. Application of Grey Modeling Method to Fitting and Forecasting Wear Trend of Marine Diesel Engines[J]. Tribology International, 2003, 36(10): 753-756.
[15] LIU S F, FORREST J, YANG Y J. Advances in Grey Systems Research[J]. The Journal of Grey System, 2013, 25(2): 1-18.
[16] 程哲, 胡茑庆, 高经纬. 基于物理模型和修正灰色模型的行星轮系疲劳裂纹故障预测方法[J]. 机械工程学报, 2011, 47(9): 78-84.
CHENG Zhe, HU Niao-qing, GAO Jing-wei. Prognosis of Fatigue Crack in Planetary Gear Sets Based on Physical Model and Modified Gray Theory[J]. Journal of Mechanical Engineering, 2011, 47(9): 78-84.
[17] WEN Lei, ZHANG Ernv. A Study on Gray Neural Network Model[C]// Proceedings of 2016 PPH International Conference on Social Science and Environment (PPH-SSE 2016 V6),Singapore Management and Sports Science Institute2016: 77-82.
[18] ZHUO Li, ZHANG Jing, DONG Pei, et al. An SA-GA- BP Neural Network-Based Color Correction Algorithm for TCM Tongue Images[J]. Neurocomputing, 2014, 134(1): 111-116.
Combination Forecasting Method of Electric Locomotive Product Demand Based on Genetic Algorithm and Grey Neural Network
WEI Wei1, HE Lei-yong1, LI Chui-hui2
(1.School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China;2.Boya Precision Industrial Equipments Co., Ltd, Hubei Xiangyang 441004, China)
In order to cope with the quicken pace of market, predict the market development in advance and formulate corresponding production scheduling plans, and enable companies to occupy a first-mover advantage in competition. The current forecasting algorithm based on gray neural network usually requires continuous and much sample data to accurately predict product demand. Aiming at the problem of low accuracy and poor reliability of prediction results of small data nonlinear systems, a grey neural network prediction method coupled with genetic algorithm is proposed. Firstly, the gray neural network model for forecasting product order demand is established based on the gray model and neural network. Secondly, the electric locomotive product is taken as an example to demonstrate the prediction performance of the model. Lastly, the genetic algorithm is used to iteratively optimize the network weights and thresholds of the mode to solve the premature convergence and improve the global optimization capability in the prediction process. The results show that the accuracy and robustness of the optimized product prediction model are improved, which verifies the feasibility of the designed method.
demand forecasting; gray model; neural network; genetic algorithm
F325.21;TB472
A
1001-3563(2022)12-0037-08
10.19554/j.cnki.1001-3563.2022.12.004
2022–01–15
国家重点研发计划(2020YFB1711402)
魏巍(1982—),男,副教授,博士生导师,主要研究方向为智能制造、制造大数据挖掘。
责任编辑:陈作
