机电产品模块划分与综合评价集成设计方法
2022-07-04李中凯裴国阳张志峰洪兆溪张婷
李中凯,裴国阳,张志峰,洪兆溪,张婷
机电产品模块划分与综合评价集成设计方法
李中凯1,2,裴国阳1,张志峰2,3,洪兆溪2,3,张婷4
(1. 中国矿业大学 机电工程学院,江苏 徐州 221116;2. 浙江大学 流体动力与机电系统国家重点实验室,杭州 310027;3. 湖州绿产智能制造有限公司,浙江 湖州 313000;4. 浙江大学 计算机科学与技术学院,杭州 310027)
为了满足机电产品日益多样化、个性化的市场需求,提高产品模块划分的稳定性与模块化方案评价的可靠性,提出产品模块划分与评价集成方法。对产品的功能结构进行分析,构建产品的量化信息模型,合理分配各量化指标的权重,构建描述组件间关系的综合矩阵。采用基于原子理论的聚类算法进行模块划分,通过改变模块粒度,稳定地得出产品模块划分的多个可行方案。通过考虑产品的模块化程度和基于信息熵的模块复杂度,构建模块化方案的综合评价模型,以确定最优的模块划分结果。采用模块划分与综合评价集成设计方法对某小型雕刻机进行模块化设计,并通过对比原子聚类算法与其他模块划分方法所得的模块化结果,验证了所提出设计方法的可行性和高效性。
模块化设计;原子理论;模块化评价;综合评价;信息熵
随着制造业的持续发展,市场对机电产品的需求也变得多样化和定制化,如何在保证产品质量和功能的同时,实现产品的快速设计和定制设计,是如今企业研究的重点[1-2]。模块化设计作为产品快速设计的一种重要方法,许多研究者对其进行了研究。程贤福等[3]考虑到模块划分过程中设计结构矩阵(Design Structure Matrix, DSM)的多样性问题,提出一种基于密度算法和设计结构矩阵的模块划分方法。张海燕等[4]以功能–原理–行为–结构设计过程模型为基础,获得了产品零部件的综合关系矩阵,并完成模块划分。Cheng等[5]通过关联设计参数间的相关性和相似性,采用基于原子理论的模块聚类算法实现对重型机床的模块划分。
产品模块划分所得的方案并不是唯一的,需对模块化方案进行评价分析,以得出最合理的模块划分结果。张浩等[6]针对产品模块化配置设计过程方案评价优选问题,构建可重构机床多目标综合优化评价模型,实现可重构机床模块化方案的优选。田楚楚等[7]从产品生命周期中的时间、成本、质量等指标出发,建立了效益评价的过程参考模型和指标体系参考模型,对机械产品的模块化效益进行综合评价。Long等[8]为了减少决策过程中主观、模糊的设计信息影响,提出了一种基于层次分析法和仿真分析结合的设计方案评价决策方法。
另外,一些学者通过模块划分与方案评价相结合的方法,完成产品的模块化设计。李玉鹏等[9]针对复杂产品的模块划分难以获得唯一方案问题,提出了一种基于混合模糊多属性决策理论的复杂产品模块划分方案评价方法。胡光忠等[10]基于灰色关联分析法研究分析线性切割机床的设计特点,利用基于模糊综合评价的模块化设计评价方法对机床进行设计。
综上所述,这些方法目前仍然对产品模块化设计具有一定的指导意义。随着机电产品复杂程度的不断提高,组件间关系的描述也愈发困难;部分模块划分方法存在模块聚类结果不稳定的状况;对模块化方案的评价也考虑得不够充分。基于上述问题,文中综合考虑组件间的关联关系,并在此基础上改进了原子聚类算法,综合考虑产品的模块化程度和模块的复杂性,构建出综合评价模型,提出机电产品模块划分与综合评价集成设计方法。此次研究的创新在于采用改进的原子聚类算法,在保证产品模块划分稳定性的同时,改善模块划分结果的合理性,通过建立综合评价模型,提高模块化方案评价的准确性。
1 构建组件综合关系矩阵
在对产品进行模块划分时,首先需要准确描述出组件之间的关系,不仅需要考虑组件间的连接关系,也需对产品的功能、结构以及物理关系等进行分析,并根据不同组件间关系的强弱程度制定合理的量化准则,从而构建组件之间的关联关系矩阵。此外,不同产品对其功能、结构等关系的重要度要求不同,合理分配各指标的权重,对构建组件间的综合关系矩阵也十分重要。
1.1 组件关系的评价准则
1)模块的一个重要特性是功能独立性。在模块划分时,将那些为实现同一功能的组件聚在一起构成模块,有助于提高模块的功能独立性,称构成这个模块的组件之间存在着功能相关性。其评价标准见表1。
表1 功能相关评价指标

Tab.1 Function-related evaluation indexes
2)除功能独立性外,结构相关性是模块的另一个重要特征。组件之间在空间几何上的物理连接、紧固、垂直度、平行度和同轴度等关系称为结构相关性。归纳起来,主要从连接关系与形位关系2个方面考虑组件之间的结构相关性。其评价标准见表2—3。
表2 连接相关评价指标

Tab.2 Connection-related evaluation indexes
表3 形位相关评价指标

Tab.3 Shape and position-related evaluation indexes
3)物理相关性是指各组件之间的能量、信息或物料间的关系。能量关联是指组件之间传递的力、扭矩、功率、电流等;信息关联是组件间传递信息(如光和电);物料关联是指组件之间物料的传递;其评价标准见表4。
表4 物理相关评价指标

Tab.4 Physical-related evaluation indexes
1.2 组件综合关系矩阵建模
对产品组件之间的功能关系、结构关系和物理关系进行分析,并确定对应的评价标准。根据相关准则,可建立产品的功能相关矩阵、结构相关矩阵(包括连接相关矩阵和形位相关矩阵)和物理相关矩阵。这些指标对于不同产品的重要程度不同,采用层次分析法确定不同指标的权重,从而得出组件间的综合关系矩阵,如式(1)所示。

式中:为综合关系矩阵;为正则化系数;,取;、、分别表示功能、结构、物理相关矩阵的权重,可通过层次分析法确定,且有;、、分别表示功能、结构、物理相关矩阵。其中,结构相关矩阵包括连接和形位相关矩阵(即和,对应权重为和)。各指标关系的权重层次结构见图1。
2 基于原子聚类算法的模块划分
模块聚类是一个复杂的、综合的、多因素影响的优化过程,很多学者对此进行了研究。其中,Smith等[11]提出了一种基于原子理论的模块聚类方法,分析组件间的接触关系,完成产品的模块划分。仅考虑组件间的接触关系,往往会得到不合实际的模块。综合考虑产品组件间的功能、结构和物理等关系,可以提高组件间关系描述的准确性,从而划分出更加合理的产品模块。
原子聚类算法是将产品中的组件模拟为原子的组成元素,即原子核和电子,原子核吸引周围的电子形成稳定的原子结构(即模块),从而达到模块划分的目的[12]。原子聚类算法的主要步骤如下。
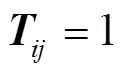
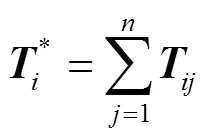
式中:为组件数。
3)确定价矩阵:
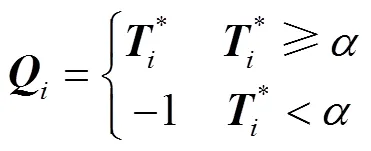

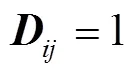
5)计算力矩阵:
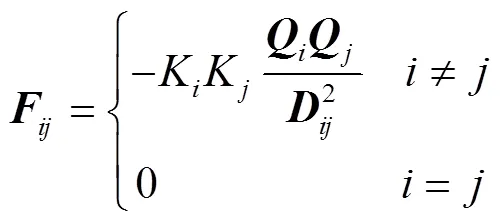
式中:K,K为库仑常量;为组件和之间的库仑力。
结合组件间的综合关系矩阵,通过设置阈值得到起约束作用的截矩阵。如式(2)所示:
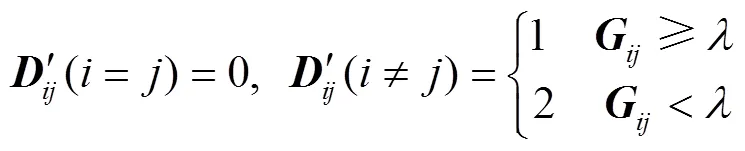
其中,
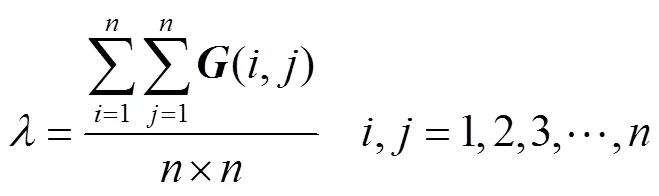
整合距离矩阵和截矩阵,可以得到更新的距离矩阵,如下:
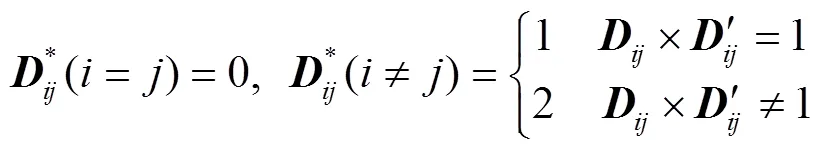
3 模块化方案的综合评价方法
对于模块划分方案,单一的评价指标通常过于片面,从多个方面进行评价分析以准确地反映出方案的优劣。其中,模块化程度作为模块化方案评价的一个重要指标,是用来描述模块内各组件之间和各模块之间的联系紧密度。在对产品进行模块化设计后,不同模块间的装配复杂度与模块的维修复杂度,也是影响模块化产品质量的重要指标。通过对不同指标的综合分析,可以提高模块评价结果的可靠性和准确性。
3.1 模块化程度的评价模型
模块划分方案的评价模型要考虑模块化程度,包括单个模块的聚合度与模块间的分离度。
1)单个模块的聚合度如下:
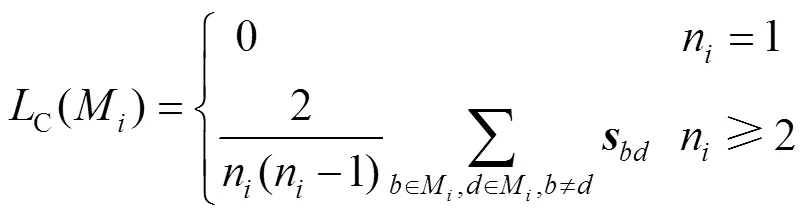
模块划分的平均聚合度如下:
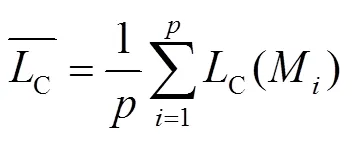
2)模块之间的分离度如下:
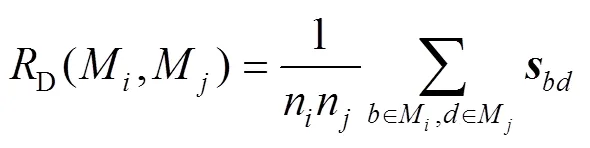
划分的所有模块的平均分离度如下:
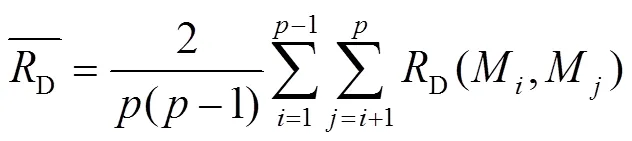
构造模块化程度的目标函数如下:
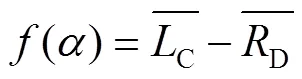
3.2 基于信息熵的模块复杂度评价模型
在信息论中,熵是用来度量信息不确定性的有效概念,也可以说明系统的复杂性[13]。每个模块划分方案都可认为是具有装配以及维修复杂度的系统,因而可以采用信息熵的方式进行计算和表达。故装配复杂度可以定义表示如下:

维修复杂度可以定义表示如下:

由上述可知,不同的模块粒度得出不同的模块划分方案,可以采用无约束离散优化模型对模块划分方案进行评价。如果模块化程度与复杂度等离散数据在较大范围内发生变化,数据中的某些变量会主导评价结果,从而掩盖了其他因素的影响,因此需要对数据进行正则化处理。
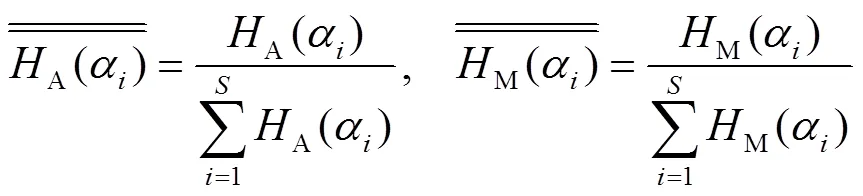
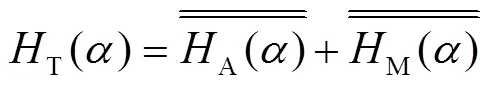
信息熵反映了模块划分方案的复杂度,并通过单个模块内聚度和模块间分离度评估方案的模块化程度。综合考虑模块划分方案的模块化程度与复杂度,构建出模块划分方案的综合评价模型。其目标函数如式(17)所示:

3.3 产品模块划分与综合评价设计方法流程
综上所述,可得产品模块划分与评价集成方法流程见图2。
具体的计算步骤如下。
1)基于对产品特点的分析,选择适合的评价指标并按照给定规则进行量化,利用层次分析法给各指标分配权重,将各指标量化信息模型与其权重结合起来,构建产品组件间的综合关系矩阵。
2)在得出综合关系矩阵后,利用原子聚类算法完成产品的模块划分,由不同的模块粒度得出不同的模块划分结果。
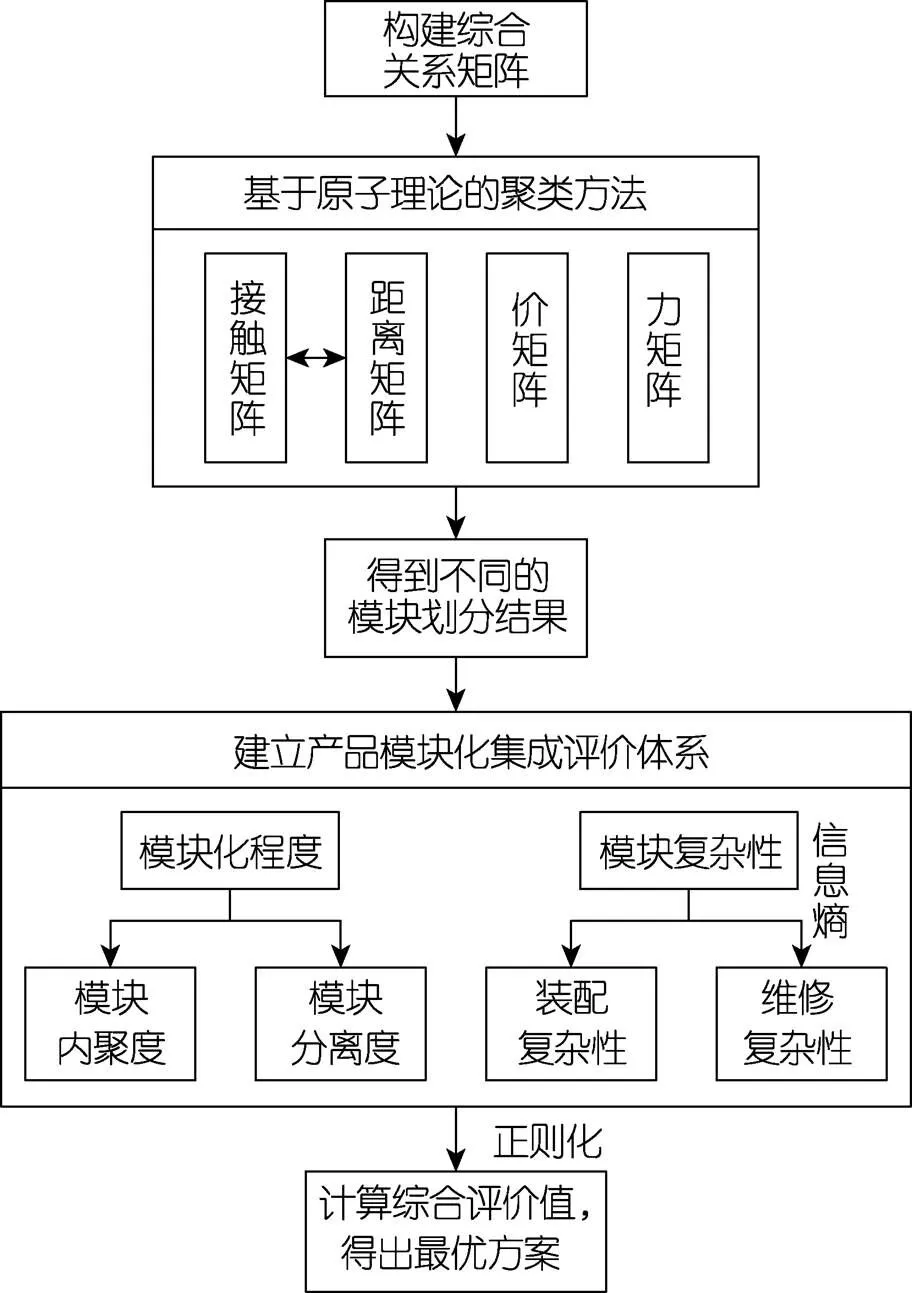
图2 产品模块划分与评价集成方法流程
3)通过分析产品的模块化程度和模块复杂度,并按照标准建立量化数学模型,构建出产品模块化集成评价体系。
4)基于评价体系对不同的模块划分方案进行评价分析,计算综合评价目标值并进行排序,从而得出最优的模块划分方案。
4 案例研究
雕刻机主要包括机械部分和电气部分两大部分,其中机械部分主要是机身和传动单元等,电气部分主要就是控制和电气元件等。由于雕刻机的电气部分多为电子元件,集成度较高,且主要集中在电控箱中,所以模块化的意义不大。文中主要对雕刻机的机械部分进行模块化研究,其主要结构见图3,其中一些较小的部件(如紧固件和螺栓等),对模块化设计的影响较小,所以对其模型进行了简化,仅考虑了雕刻机的主要部件。雕刻机的主要组件包括:机架、导轨、丝杆、步进电机、主轴电机等。通过对雕刻机功能和结构进行分解,可得不同指标下组件间的关系强度,从而得出雕刻机的综合信息模型。基于上述的模块划分流程,采用基于原子理论的聚类方法,完成对雕刻机的模块划分工作,并对模块划分结果进行分析评价。
通过分析雕刻机的功能和结构特点,建立组件间的功能关系矩阵、结构关系矩阵、物理关系矩阵和组件的接触矩阵等基础的产品信息模型。结合上述的模块设计流程,在MATLAB的编程环境中进行编译计算,得出雕刻机的综合关系矩阵和原子聚类算法中的价矩阵、力矩阵等模块信息矩阵,从而完成雕刻机的模块划分。其中,雕刻机的综合关系矩阵见表5。
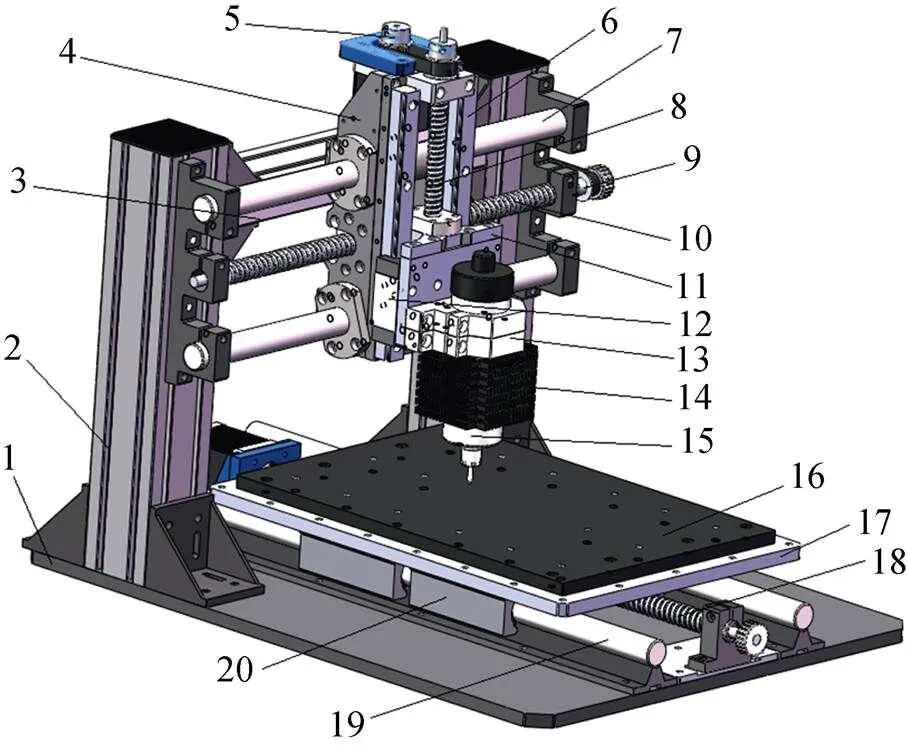
1–机身底板;2–立柱;3–横梁;4–x轴拖板组合;5–z轴同步带轮组合;6–直线导轨;7–x轴带座丝杆光轴;8–z轴滚珠丝杆;9–x轴同步带轮组合;10–x轴滚珠丝杆;11–z轴底板;12–直线导轨滑块;13–主轴座;14–主轴散热装置;15–主轴;16–PVC台面;17–y轴底板;18–y轴滚珠丝杆;19–y轴带座光轴;20–SBR滑块。
表5 雕刻机的综合关系

Tab.5 Comprehensive relationship matrix of engraving machine
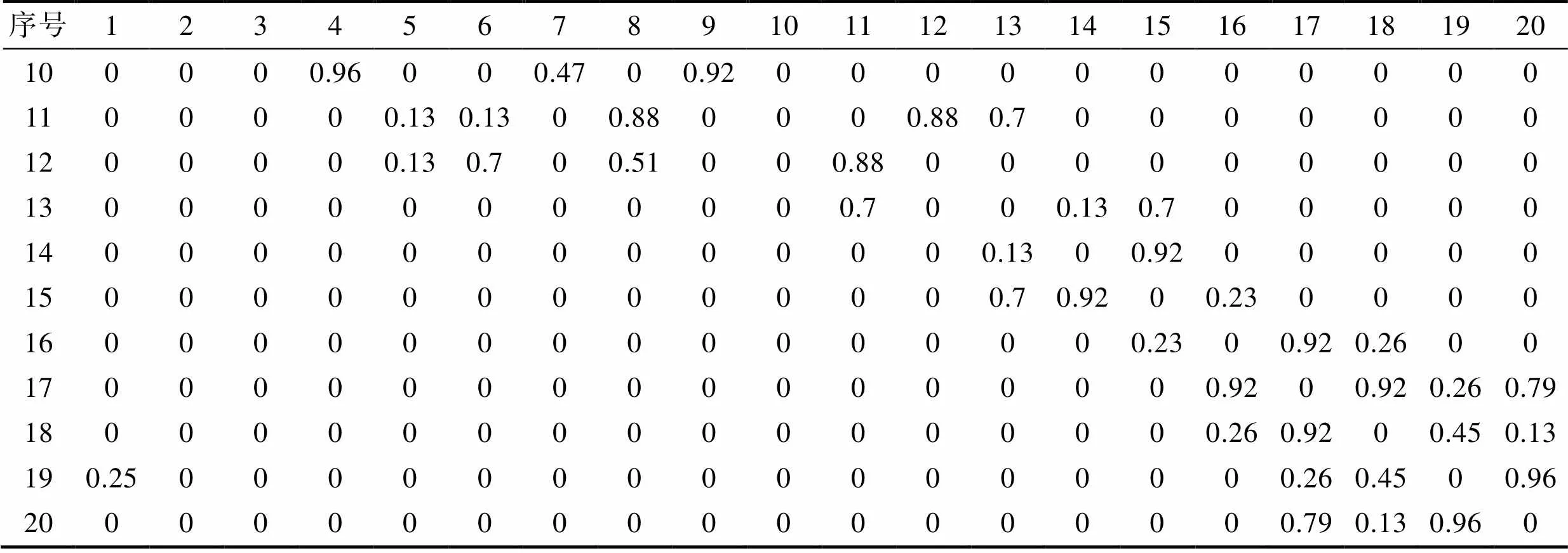
续表5
根据原子聚类算法,不同的模块粒度划分得出不同的模块划分方案。采用模块划分方案的综合评价模型,可以对模块划分方案进行评价。其中,模块化程度的评价参数可由雕刻机的综合关系矩阵获得,装配复杂度的评价参数可由总接触矩阵*获得(即组件的接口数),维修复杂度的评价参数(即组件间的相对易损率)则需通过层次分析法来确定。其结果如下:
经过上述计算,可得雕刻机的模块划分方案与评价计算结果见表6。
表6 模块划分方案及评价结果

Tab.6 Module division schemes and evaluation results

图4 雕刻机模块化结果
此外,我们使用模糊聚类方法[14]与Tseng等[15]使用的GGA算法分别对雕刻机进行模块划分,得出不同的模块划分结果见表7。
表7 模块划分方案对比

Tab.7 Comparison of module division schemes
经过比较,人们不难发现上述3种模块聚类算法得出的模块划分方案既有相同部分,也存在一些差别。与原子聚类算法得出的方案相比,模糊聚类方法所得的方案分别将轴移动拖板模块和轴滚珠丝杆模块、轴可移动平台模块和轴滚珠丝杆模块整合起来,形成了轴移动模块和轴移动模块,其功能复杂度和生产制造复杂度均有所提高;GGA方法得出的方案与原子聚类算法所得方案区别较小,仅为个别组件间的划分差异,但其计算过程较为复杂,且在运算过程中存在陷入局部最优解的情形。综上所述,文中的模块划分方法具有划分过程简单,划分结果稳定可靠等特点。
5 结语
该研究建立了基于模块划分与综合评价的模块化集成设计方法,采用基于原子理论的模块划分方法与多属性的综合评价体系,实现了机电产品的模块化设计。通过分析产品的功能结构与组件间的物理传递关系,构建出组件间的综合关系矩阵;基于组件间的综合关系矩阵,利用原子聚类算法对产品组件进行划分,得出模块划分方案;考虑产品的模块化程度和模块复杂度,建立模块划分方案的综合评价模型,计算评价模型的综合目标值,从而获得最佳的模块划分方案。最后以某种型号的雕刻机为例,验证了该模块化设计方法的有效性。此外,该研究具备延展性,一方面可以加强产品组件间关联信息的自动化获取;另一方面可以引入其他评价指标(如环境、经济等因素),构建更加综合全面的模块评价模型。
[1] 顾新建, 马步青, 顾复, 等. 产品模块化中的若干智能方法[J]. 机械工程学报, 2021, 57(17): 1-9.
GU Xin-jian, MA Bu-qing, GU Fu, et al. Some Intelligent Methods in Product Modularization[J]. Journal of Mechanical Engineering, 2021, 57(17): 1-9.
[2] 赵京, 张晓丹, 张自强, 等. 模块化机械装备及其设计方法研究综述[J]. 华中科技大学学报(自然科学版), 2021, 49(10): 19-29.
ZHAO Jing, ZHANG Xiao-dan, ZHANG Zi-qiang, et al. Review of Modular Mechanical Equipment and Modular Design Methods[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2021, 49(10): 19-29.
[3] 程贤福, 万冲, 邱浩洋, 等. 基于密度算法和DSM的模块划分方法[J]. 华东交通大学学报, 2019, 36(2): 105-110.
CHENG Xian-fu, WAN Chong, QIU Hao-yang, et al. A Module Partition Approach Based on Density Algorithm and Design Structure Matrix[J]. Journal of East China Jiaotong University, 2019, 36(2): 105-110.
[4] 张海燕, 侯力, 罗岚, 等. 变双曲圆弧齿线圆柱齿轮专用机床的模块化设计[J]. 机械工程学报, 2021, 57(3): 77-86.
ZHANG Hai-yan, HOU Li, LUO Lan, et al. Modular Design for Machine Tools of Variable Hyperbolic Circular-Arc-Tooth-Trace Cylindrical Gear[J]. Journal of Mechanical Engineering, 2021, 57(3): 77-86.
[5] CHENG Qiang, GUO Yi-liang, LIU Zhi-feng, et al. A New Modularization Method of Heavy-Duty Machine Tool for Green Remanufacturing[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2018, 232(23): 4237- 4254.
[6] 张浩, 裘乐淼, 张树有, 等. 基于集对分析的可重构机床配置方案评价方法[J]. 浙江大学学报(工学版), 2015, 49(7): 1232-1241.
ZHANG Hao, QIU Le-miao, ZHANG Shu-you, et al. Evaluation Method Based on Set Pair Analysis for Configuration Scheme of Reconfigurable Machine Tools[J]. Journal of Zhejiang University (Engineering Science), 2015, 49(7): 1232-1241.
[7] 田楚楚, 石浩, 顾复, 等. 机械产品模块化效益评价方法及应用[J]. 成组技术与生产现代化, 2018, 35(2): 1-8.
TIAN Chu-chu, SHI Hao, GU Fu, et al. Modular Benefit Evaluation Method and Application of Mechanical Products[J]. Group Technology & Production Modernization, 2018, 35(2): 1-8.
[8] LONG H J, WANG L Y, SHEN J, et al. Product Service System Configuration Based on Support Vector Machine Considering Customer Perception[J]. International Journal of Production Research, 2013, 51(18): 5450-5468.
[9] 李玉鹏, 连晓振, 卢成, 等. 基于混合模糊多属性决策的复杂产品模块划分方案评价[J]. 上海交通大学学报, 2017, 51(11): 1374-1382.
LI Yu-peng, LIAN Xiao-zhen, LU Cheng, et al. Evaluation Approach to Rank Module Partition Schemes of Complex Products Based on Hybrid Fuzzy Multi-Attribute Decision Making[J]. Journal of Shanghai Jiao Tong University, 2017, 51(11): 1374-1382.
[10] 胡光忠, 朱龄, 乔鸿静, 等. 基于灰色关联分析法的线切割机床模块化设计评价研究[J]. 包装工程, 2019, 40(18): 53-60.
HU Guang-zhong, ZHU Ling, QIAO Hong-jing, et al. Evaluation on Modular Design of Wire Cutting Machine Based on GRA[J]. Packaging Engineering, 2019, 40(18): 53-60.
[11] YOU Z H, SMITH S. A Multi-Objective Modular Design Method for Creating Highly Distinct Independent Modules[J]. Research in Engineering Design, 2016, 27(2): 179-191.
[12] 姜星月, 张秀芬. 一种改进的绿色模块化设计方法研究[J]. 机电工程, 2019, 36(5): 451-457.
JIANG Xing-yue, ZHANG Xiu-fen. An Improved Green Modular Design Method[J]. Journal of Mechanical & Electrical Engineering, 2019, 36(5): 451-457.
[13] 孙之琳, 王凯峰, 陈永亮, 等. 产品可适应设计评价的信息熵方法[J]. 工程设计学报, 2021, 28(1): 1-13.
SUN Zhi-lin, WANG Kai-feng, CHEN Yong-liang, et al. Information Entropy Method for Product Adaptable Design Evaluation[J]. Chinese Journal of Engineering Design, 2021, 28(1): 1-13.
[14] WU Yong-liang, MAO Bao-quan, XU Li, et al. The Evaluation of Module Division Programme Based on Information Entropy[J]. Advanced Materials Research, 2012, 479-481: 1592-1595.
[15] TSENG H E, CHANG C C, LI J D. Modular Design to Support Green Life-Cycle Engineering[J]. Expert Systems With Applications, 2008, 34(4): 2524-2537.
Integrated Design Method for Modular Division and Comprehensive Evaluation of Electromechanical Products
LI Zhong-kai1,2, PEI Guo-yang1, ZHANG Zhi-feng2,3, HONG Zhao-xi2,3, ZHANG Ting4
(1. School of Mechatronics Engineering, China University of Mining & Technology, Jiangsu Xuzhou 221116, China;2. State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University, Hangzhou 310027, China; 3. Huzhou Lvchan Intelligent Manufacturing Co., Ltd., Zhejiang Huzhou 313000, China;4. School of Computer Science and Technology, Zhejiang University, Hangzhou 310027, China)
This paper aims to meet the increasingly diversified and personalized market demand of mechanical and electrical products, and improve the stability of product module division and the reliability of modular scheme evaluation, an integrated method for modular division and evaluation was proposed. The paper analyzed the function and structure of the product, a quantitative information model of the product was built up. The weight of each quantitative index was distributed reasonably and comprehensive matrixes describing the relationship between components were constructed. The clustering algorithm based on atomic theory was used for module division. By changing the module granularity, several feasible schemes for product module division were obtained stably. In order to construct a comprehensive evaluation model of modular scheme to determine the optimal module division result, the modular degree of products and the module complexity based on information entropy were considered. The modular design of a small engraving machine was carried out by using the integrated design method of module division and comprehensive evaluation. Furthermore, by comparing the modular results obtained by atomic clustering algorithm and other module division methods, the feasibility and efficiency of the proposed design method were verified.
modular design; atomic theory; modular evaluation; comprehensive evaluation; information entropy
TH122;TP391;TB472
A
1001-3563(2022)12-0030-07
10.19554/j.cnki.1001-3563.2022.12.003
2022–01–25
国家自然科学基金(51475459,52105281);湖州市重点研发计划(2019ZD2010);浙江省重点研发计划(2022C01196)
李中凯(1980—),男,博士,副教授,博士生导师,主要研究方向为现代设计方法、智能设计。
张志峰(1991—),男,博士生,主要研究方向为大型机电装备数字化设计。
责任编辑:陈作
