Open-MUSIC：基于度量学习与特征子空间投影的电磁目标开集识别算法

杨 柳，利 强，邵怀宗

（电子科技大学信息与通信工程学院，四川成都 611731）

1 引言

近年来，电磁频谱已成为不可或缺的国家战略资源，是继陆、海、空、天、网之后的第六维作战空间，对电磁频谱的智能认知是实现制电磁权的关键. 然而，战场复杂、开放的电磁空间和不断出现的未知辐射源，给电磁频谱认知带来了巨大挑战. 其中，从侦收信号中快速、准确地识别出辐射源是未知目标还是已知目标的未知工作模式，是电磁目标认知需要解决的首要问题.由于缺少未知目标训练样本，对于未知目标的识别本质上属于开集识别［1］（open set recognition），也被称为开放世界识别［2］（open world recognition）或开放类识别（open category learning），本文使用开集识别这一术语.在开集识别的测试中，测试样本可能来自训练集所包含的类别以外的数据，开集识别算法的目的是学习一种分类预测模型，将已知类的样本分类成正确的类，并识别出未知类的样本.

与开集识别相对应的是闭集识别，即训练集中的类别和测试集中的类别是一致的，数据集中所有的样本的类别都是已知的，没有未知类别的样本. 所以闭集识别在训练集与测试集数据分布相同的假设下，只需要寻找各个类别之间的分界线，将各类别分开即可. 自从2010 年AlexNet［3］在ImageNet LSVRC-2010（Ima⁃geNet Large-Scale Visual Recognition Challenge-2010）上夺冠，基于深度学习的分类识别技术在图像、语音和电磁等领域受到了极大的关注. 但是，将现有基于闭集的识别网络直接应用到开集识别中，仍然面临许多问题.

2 相关工作与背景

2.1 电磁信号识别

近年来，基于深度学习的电磁信号识别取得了不错的成绩. O’Shea 等人［4］使用残差神经网络［5］在考虑了载波频偏、多径衰落和信道损伤等的情况下解决了信号分类识别问题，并讨论了设计此类模型的注意事项. Peng 等人［6］使用AlexNet 和GoogLeNet 来处理调制分类问题，体现了深度学习在电磁领域的显著优势.Duan 等人［7］提出了一种多载波波形自动分类方法，并利用主成分分析抑制加性高斯白噪声，降低神经网络的输入维数. 此外，Wong 等人［8］使用卷积神经网络来估计每个发射器的同向/正交（I/Q）不平衡参数.Huang等人［9］提出了一种用于自动调制分类的压缩卷积神经网络，并提出了使用压缩损失来训练该网络.Zhang 等人［10］通过使用频带选择、信噪比选择和样本选择来减少模型训练所需的时间，并证明了深度学习在无线干扰识别的可行性.Liang 等人［11］提出了一种基于深度学习的功率控制方法，旨在解决最大化衰落多用户干扰信道总和率的非凸优化问题.

2.2 开集识别

本文主要研究开集识别问题，即在训练阶段没有未知类的信息：既没有这些类的实例信息，也没有属性信息. 训练完成后，在测试和使用阶段，算法需要对未知类的实例样本进行分辨. 对于开集识别问题，如今已经有了一些研究，这些研究大体可以分为两类：基于判别模型和基于生成模型.

从基于判别模型的方面看，主要有基于传统机器学习的方法和基于深度神经网络的方法. 传统的机器学习方法通常是基于训练数据与测试数据分布相同的假设的，为了使这些方法能够运用在开集识别问题里，学者们进行了许多研究. Cevikalp［12，13］在SVM（Support Vector Machine）的基础上，对已知类样本增加约束，提出了最佳拟合超平面分类器（best-fit hyperplane classi⁃fier）.Bendale 等人［2］通过扩展最近类均值（nearest class mean）分类器，开发了最近邻非离群点（Nearest Neigh⁃bor non-Outlier，NNO）算法来解决开集识别问题. NNO算法根据样本与各个已知类中心的距离进行分类，如果所有已知类的分类器都判断该样本不属于已知类，则将该样本判定为未知类. 对于深度神经网络来说，其本身就具有强大的学习表示能力，分类时通常使用SoftMax 层与交叉熵损失，使得其本质上具有封闭性.对于此问题，Bendale 等人［1］提出了OpenMax 模型，首先用SoftMax 层通过最小化交叉熵损失来训练网络，然后计算训练样本的特征到其对应类的平均特征向量的距离，并用于拟合每个已知类单独的威布尔分布，根据韦布尔分布拟合分数对特征向量进行重新分布，最后再利用SoftMax 计算已知类和未知类的概率. Dhamija 等人［14］将SoftMax 与新的熵开集损失和Objectosphere 损失.Shu［15］提出了DOC（Deep Open Classifier）模型，采用了1-vs-rest 的Sigmoid 层将SoftMax 替代. Liu 等人［16］采用动态元嵌入结合了直接图像特征和相关的记忆特征，其特征范数表明对已知类的熟悉程度，以此来实现对未知类的识别. Hassen 等人［17］提出了ii-loss 与交叉熵损失共同训练网络，使得其产生的特征更适合开集识别场景. 几乎所有的基于判别模型的开集识别算法都需要指定阈值，阈值在算法中起到了非常关键的作用，后面会对阈值的选定过程进行讨论说明.

从基于生成模型的方面看，Ge 等人［18］采用条件生成网络来生成未知类的样本，并与OpenMax 结合，提出了G-OpenMax 算法，可以对生成的未知类样本进行概率估计. Yu 等人［19］提出了对抗样本生成框架（adver⁃sarial sample generation framework），可以用它生成与已知类样本相近的未知类样本，必要时也可以生成已知类样本来扩充已知类数据集.Chen 等人［20］提出了一种称为对抗互易点学习（Adversarial Reciprocal Point Learning，ARPL）的方法，以在不损失已知分类精度的情况下最小化已知分布与未知分布的重叠部分. 这些方法已经取得了一些成果，但如何生成更有效的未知类样本仍需探索.

2.3 度量学习

在机器学习中，对高维数据进行各种形式的降维，主要是为了学习数据表示，即寻找一个可以更好地表示数据特征的低维空间，这个数据特征可以直接用于解决任务. 度量学习是传统机器学习的一种，就是在空间中寻找合适的空间或合适的距离度量函数，并用距离来度量样本之间的相似度. 通过训练，相似样本之间的距离小，不同样本之间的距离大.

传统的度量学习主要是学习一个距离度量函数.例如马氏距离［21］需要学习一个（半）正定对称矩阵. 在深度度量学习中，主要是利用一定的损失函数作为距离度量，让网络学习一个低维的特征空间（通常称为Embedding），达到同类聚合和异类分离的效果. 这个距离度量可以固定，不需要学习，比如欧式距离和余弦距离. 度量学习大致可以分为基于样本对和基于代理［22］两种. 许多度量学习算法都是基于样本对的，主要有Contrastive Loss 和Triplet Loss等. 基于代理的方法则使用全局信息进行优化，例如Center Loss 和Proxy-NCA等.

3 问题描述

开集识别的问题可以用以下数学语言来描述：给定一个训练集T={(xi,yi)|i=1,2,…,N}，其中xi∊Rsample，训练集中样本的类别集S={1,2,…,K}，其中yi∊S. 在训练阶段，只能访问和使用训练集中的样本及其标签，而没有任何其他未知类的信息；而在测试阶段，有测试集TO={(xi,yi)|i=1,2,…,M}，测试集的样本类别集合SO={1,2,…,K,K+1,…,P}，其中K+1,…,P表示训练阶段未出现的类别. 鉴于上述定义，开集识别算法需要将以下风险最小化，即

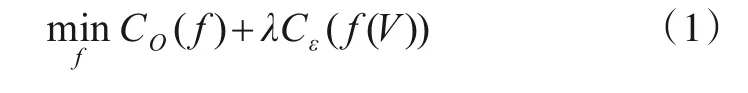
其中，f是需要训练的开放集识别模型；CO和Cε分别代表开放空间风险和经验风险；V是训练数据，且只包含已知类；λ为常数. 这个风险旨在平衡经验风险和开放空间风险，在已知样本识别率高的情况下，将未知样本分辨出来.

4 算法描述

针对以上问题，本文提出基于特征子空间分解与投影的开集识别Open-MUSIC 算法. 该算法主要包括3个步骤.

步骤1 通过结合交叉熵损失与中心损失来训练一个分类网络，训练完成后，该分类网络输出层的前一层输出结果用作数据特征提取，得到从数据到特征的映射模型，如图1所示.

图1 基于神经网络的映射特征模型训练算法

步骤2 将所有训练样本输入模型中，得到各个已知类的中心特征向量，将各个向量组合形成已知类中心特征矩阵，对该矩阵进行正交子空间分解，得到其值域子空间与零域子空间，用于步骤3 中评估指标的计算，具体如图2所示.

图2 特征子空间分解并计算投影比值

步骤3 将测试数据输入步骤1 中的特征提取网络，并将提取到的特征分别投影到步骤2中的值域子空间和零域子空间，并计算投影长度比值. 若比值大于设定的阈值，则判定为属于已知类；否则，为未知类，具体如图3 所示. 值得注意的是，阈值的设定对性能影响较大，后面本文会对阈值的设定进行详细讨论.

图3 确定阈值或判决方案

综上所述，算法主要包含：获得映射特征、特征子空间分解并计算投影比值、阈值确定. 下面对各步骤进行详细说明.

4.1 获得映射特征

获得映射特征就是只使用已知训练数据，学习一个模型，完成样本空间到特征空间的映射，即F(x)：Rsample→Rd. 在开集识别环境下，映射的特征需要满足2 个条件：缩小类内距离，扩大类间距离. 前者保证从已知目标数据中学习到目标特征最本质的表征，而后者保证已知和未知类边界划分更容易，使得式（1）中开放空间风险与经验风险都较小. 该想法与Fisher 判别法类似，Fisher 判别法目标是通过最大化2类质心距离与类内距离的比值，来得到一个映射矩阵，可以将2 类样本映射到一维空间. 而本文可以使用神经网络来学习映射函数，将样本投影映射到高维空间.

一般情况下，映射网络为卷积神经网络，且采用交叉熵损失来监督训练网络，该损失函数由如下公式定义：

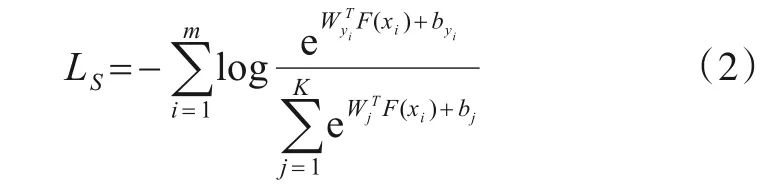
其中，xi为训练集中的第i个样本；yi为该样本的分类标签；F(x)为该样本通过模型映射得到的映射特征，且F(x)∊Rd；Wj∊Rd为分类器的最后一个全连接层权重W第j行；b为该全连接层的偏置；m和K分别为训练批大小与已知类个数.

由其定义可知，最小化交叉熵损失只能保证通过映射网络得到的特征可分，即在一定程度上可以将各类之间的距离拉大，但并不能保证每类类内聚合. 为此，本文在交叉熵损失基础上，引入中心损失，即

并使用交叉熵损失与中心损失联合监督训练网络［23］，联合的损失由下式定义：

其中，ci为第i类的中心特征向量；λ≥0 为常数，用来平衡两种损失函数所占的比重，若λ为0，则该损失函数与交叉熵损失相同. 交叉熵损失主要对类间的分离做贡献，中心损失主要对类内的聚合做贡献. 其网络结构示意图如图1 所示，其中Embedding 向量为维度为d（>K）的特征. 映射网络参数的训练过程如算法1所示.

算法1 映射网络训练算法输入:T:训练数据集(xi,yi)N i=1 θC,W:映射网络与最后一层全连接层参数cj| j=1,2,…,K:中心特征λ,α,μ:超参数输出:θC 1:WHILE NOT 网络收敛条件DO 2:Lt=Lt S+λLt C 3:S ∂Lt ∂Lt C∂Lt∂xi=∂xi+λ∂xi 4:Wt+1=Wt-μ∂Lt∂Lt∂Wt =Wt-μ S∂Wt 5:θt+1 C =θtC-μ∑i∂xi∂Lt∂xi·N()θtC Nδ(yi=j)(cj-xi)6:ct+1j =ct j-α∑i Nδ(yi=j)1+∑i 7:t ←t+1 8:END WHILE 9:返回θC

4.2 特征子空间分解

在完成数据特征提取后，已有多种方法对特征进行处理以适应开集识别场景. 比如，采用通过SoftMax层后的概率计算熵，并制定阈值，熵大于阈值，则为未知类；熵小于阈值，则为已知类. 或者采用离群值，计算实例到K个已知类中最近类平均值的距离作为决策量［24］. 受子空间MUSIC（MUltiple SIgnal Classification）算法启发，本文提出一种基于特征子空间分解投影的开集识别算法.

其中，中心特征矩阵D由所有已知类的中心特征向量组成. 对D进行奇异值分解，得到它的值域子空间和零域子空间，两个空间相互正交. 容易看出，如果待分类样本来自某个已知类，其特征可以近似由D的值域子空间刻画，因此，其在D的零域子空间投影近似为零.同样地，如果待分类样本为未知类，其特征无法由已知类的中心特征矩阵D完全表征，即未知类特征在D的零空间有（较大）投影. 因此，可以利用已知类和未知类在D的两个正交子空间投影长度的差异来区分已知和未知. 基于此，定义如下比值：

4.3 阈值确定

算法2 子空间投影比算法输入:F:特征映射网络T:训练数据集(xi,yi)N i=1 K:已知类个数x:测试样例输出:该测试样例的比值ς 1:Ni ←0,i=1,2,…,K 2:FOR(xi,yi)in T DO 3:Ayi Ni+1 ←F(xi)4:Nyi ←Nyi+1 5:END FOR 6:FOR k ∊[1,2,…,K]DO 7:FOR n ∊[1,2,…,Nk]DO 8:Bk ←Bk+Akn/Nk 9:END FOR 10:END FOR 11:D ←[B1,B2,…,BK]T 12:v1,v2 ←SVD(D)=UΣVT=[U]Σ[v1,v2]T 13:对于测试样例x有A ←F(x)14:ς=‖‖a·v1 2‖‖a·v2 2 15:返回ς

如式（9）所示，阈值直接用于判断是否是未知类的样本，且阈值的好坏直接影响算法的准确性. 下面主要介绍两种确定阈值的方法.

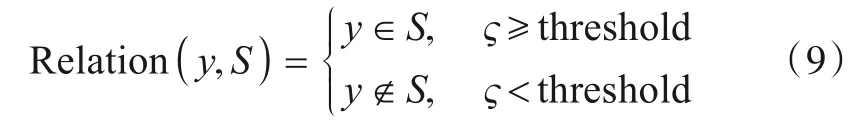
4.3.1 通过正确率确定阈值

第一种方法，阈值只使用已知类样本来确定. 将所有已知类样本经过映射模型，获得特征后，可由式（8）计算该样本比值，并按从大到小排序，其序列记为S.然后固定已知类识别准确率Accuracy，如：90%，95%或99%，划分阈值门限为S中下标为round(length(S)∙Accuracy)所对应的比值作为阈值. 实验发现，依据已知类准确率的划分方式，可避免门限划分过低，导致未知类误判为已知类.

4.3.2 通过似然比确定阈值

第二种方法，利用生成对抗模型生成一些与训练样本相近的负样本，与训练样本或生成的正样本一起，经过步骤1 和步骤2 后，得到各个样本的比值，画出统计直方图（图4）. 由图可以看出，假定正样本的比值与负样本的比值遵循某个分布，如正态分布或威布尔分布等，则可以用似然比对测试集做分类预测. 以威布尔分布为例，有

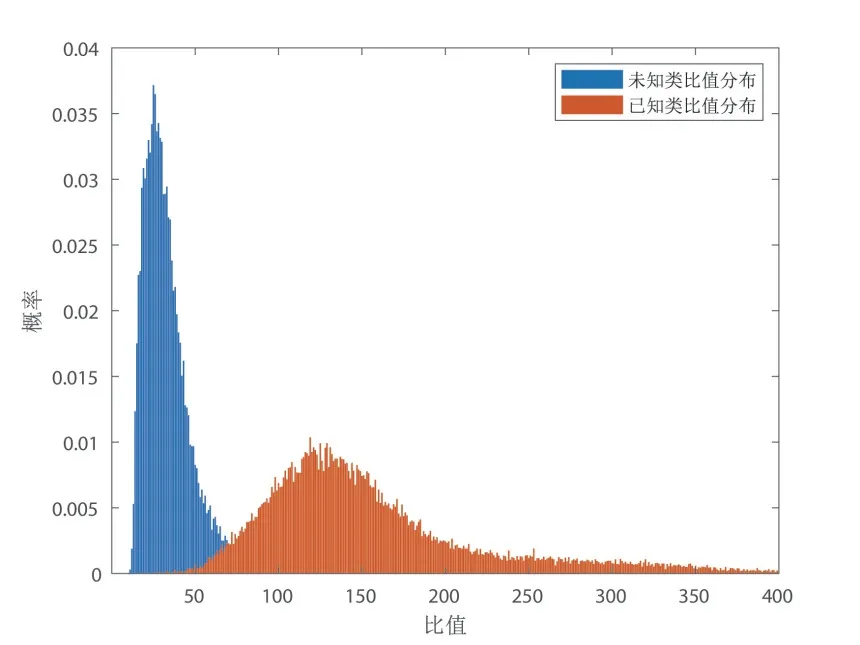
图4 已知类与未知类比值分布直方图

其中，H0为未知类；H1为已知类；k0,λ0,k1,λ1可以通过正负样本的比值计算出来.

当p(H0|x)>p(H1|x)时，表示该样本属于未知类；否则该样本属于已知类. 而由贝叶斯公式可知，p(H0|x)>p(H1|x) 与p(x,H0)>p(x,H1)等价，而p(x,H)=p(x|H)∙p(H)，故设

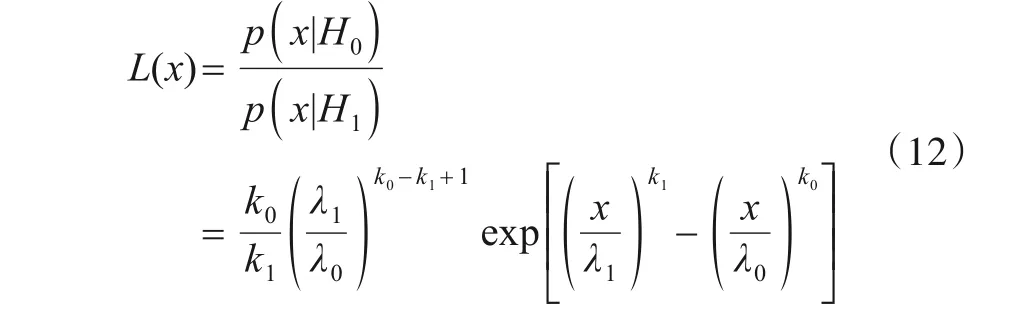
假设样本属于已知类与未知类的先验概率相等，即p(H0)=p(H1)=0.5，则有

所以，有判决准则：

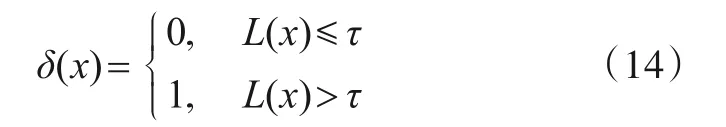
即L(x)≤τ时，该样本属于未知类；否则，该样本属于已知类.

5 实验与结果分析

在本节中，我们将在3个数据集上进行算法有效性验证.3 个数据集分别为MNIST 手写数字数据集、雷达PDW数据集、无人机信号数据集.

本文主要使用识别精度（Accuracy）、F 值（Fmeasure）与ROC 曲线（Receiver Operating Characteristic Curve）下的面积AUC-ROC来衡量各种算法在开放集上的效果，F-measure由下式定义：

其中，Precision为准确率，Recall为召回率，F-measure为准确率与召回率的调和平均值. Precision 与Recall 定义为

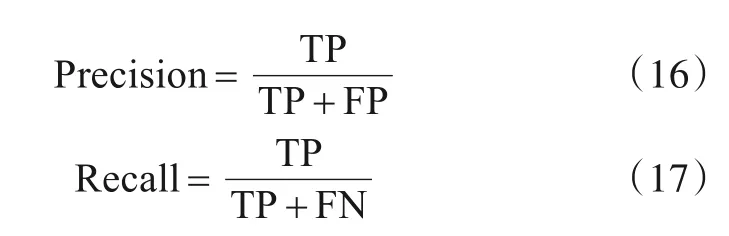
其中，TP 为将正类预测为正类的数量；FP 为负类预测为正类的数量，即误报率；FN 为将正类预测为负类数，即漏报率.

第二个指标为准确率，计算式为

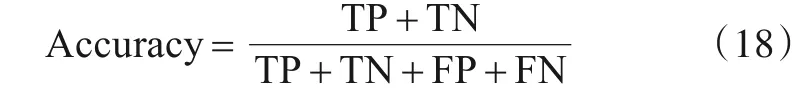
其中，TP、FP、FN 与上述相同；TN 为将负类预测为负类的数量.

由于F-measure 与Accuracy 受阈值影响较大，故引入ROC 曲线下的面积AUC-ROC 来衡量算法的性能.ROC 曲线又称接受者操作特征曲线. 该曲线最早应用于雷达信号检测领域，用于区分信号与噪声. 后来人们将其用于评价模型的预测能力. 对于一个二分类模型，其阈值可能设定或高或低，每种阈值的设定会得出不同的FP 和TP，将同一模型每个阈值的（FP，TP）坐标都画在ROC 空间里，就成为特定模型的ROC 曲线. 而ROC 曲线与FP 轴所包围的面积越大，表示该模型性能越强.

5.1 数据集描述

5.1.1 MNIST手写数字数据集

MNIST 数据集是手写数字的灰度图像数据集，数据集中共包括6 万多张训练图像样本与1 万多张测试图像样本，共分为10 类，且每个样本大小为28×28. 因为该数据集中的灰度图像样本已经可以直接在模型中使用，所以不需要对数据集做任何预处理操作.

在MNIST 数据集中，样本分为10 类. 为适应开集识别场景，我们选取0，1，2，3，4，5 为已知类进行训练；设定6，7，8，9为未知类，在训练阶段不可见.

5.1.2 多功能雷达工作模式数据集

多功能雷达数据集是通过仿真生成的多功能雷达不同工作模式的脉冲描述字（PDW）数据，一共包含55个已知工作模式和6 个未知工作模式，每条PDW 数据主要包括：脉冲到达时间（TOA）、载波频率（RF）、脉冲宽度（PW）、脉冲幅度（PA）、脉冲到达角度（DOA）等参数. 由于在侦收中，PA和DOA受环境影响较大，不作为工作模式识别的特征. 已知和未知模式分别包含757个和120个样本，每个样本包含100个脉冲记录.

在使用雷达数据集之前需要对数据做预处理. 将TOA 转为脉冲重复间隔（PRI）后，每条PDW 样本的PRI，RF 和PW 作为3 个通道，形成3×100 的类图片样本. 为了更适合CNN 提取特征，将样本延展为3×100×100 的图片，并将每个通道按下式进行归一化，得到预处理后的数据集.

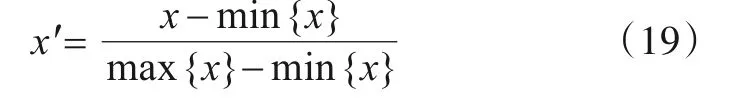
在训练阶段，随机将757个已知类样本划分为训练集（637 个样本）与测试集（120 个样本），训练集主要用于模型训练，测试集可与未知类数据（120个样本）共同用于开集识别测试.

5.1.3 无人机个体识别信号数据集

无人机个体识别信号数据集由实际采集的9 款无人机时域信号数据组成，用于对无人机个体指纹的识别. 部分时域信号如图5所示.

对无人机采集信号需要进行预处理. 预处理主要包含提取有效信号部分和将时域信号处理为类图片形式，方便CNN 提取特征. 采用能量检测方法对有效信号部分进行提取切片，即计算窗内数据的能量，大于阈值则为信号部分，小于阈值则为噪声部分. 之后对提取出的有效信号进行短时傅里叶变换（Short-Time Fourier Transform，STFT）形成时频图片. 图6 给出了图5 有效信号在STFT变换后的时频图.

图5 无人机信号时域图

图6 无人机信号时频图

通过上述预处理过程，为每架无人机提取了600张时频图样本，共5 400 个样本，并将9 架无人机中的5 架作为已知类，其余4 架作为未知类，已知类和未知类样本大小分别为3 000和2 400.

5.2 实验设计

本实验将Open-MUSIC 与OpenMax［1］、OLTR［16］、iiloss［17］和ARPL［20］在MNIST 手写数字识别、雷达工作模式识别和无人机个体指纹识别上进行实验对比，通过F-measure、Accuracy 与AUC-ROC 等指标对各个模型进行评估.Open-MUSIC 在3 个数据集上映射网络模型分别如表1～表3所示.

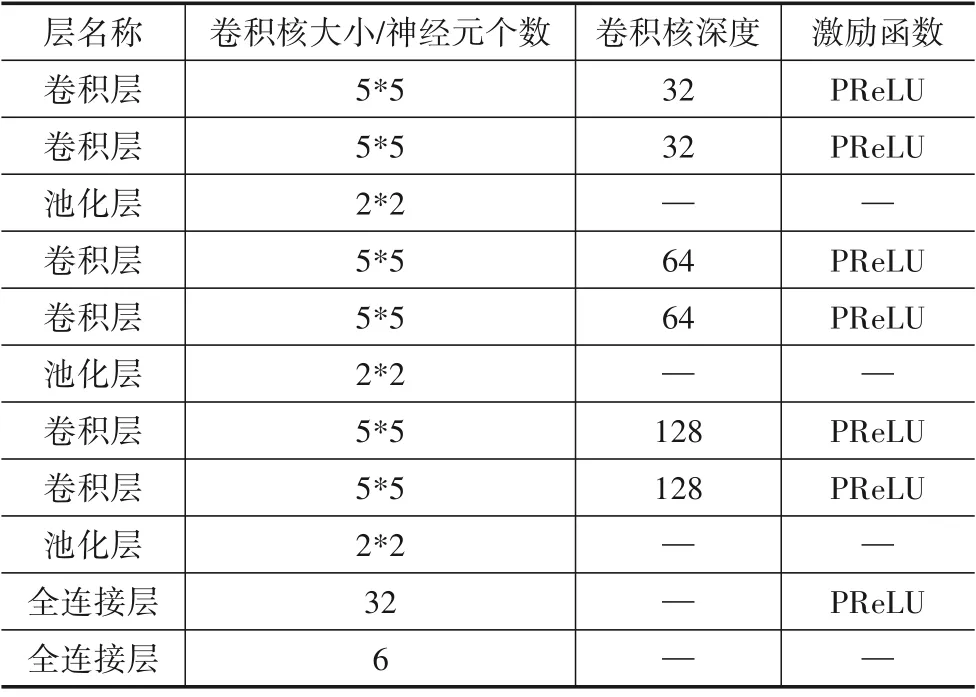
表1 MNIST数据集所使用特征映射网络参数表

表3 无人机数据集所使用特征映射网络参数表

5.3 实验结果及分析

表4～表6 分别给出了各个算法在MNIST 数据集、雷达数据集与无人机信号数据集上的结果.

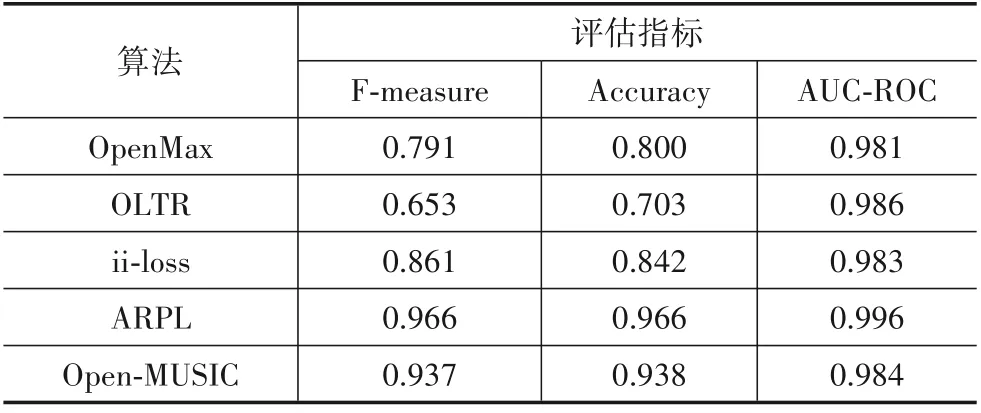
表4 MNIST数据集实验结果

表6 无人机信号数据集实验结果

在MNIST 数据集上，ARPL 算法在3 个指标上都表现最佳. Open-MUSIC 算法虽然AUC-ROC 略低于其他算法，但是F-measure 与Accuracy 等指标都仅次于ARPL 算法，优于其他方法.OpenMax、OLTR 和ii-loss 等方法虽然AUC-ROC 较高，但其余两个指标较低，这表明这些算法的性能受阈值影响较大，也说明了Open-MUSIC设定的阈值效果较好.

在雷达数据集上，Open-MUSIC 较其他方法性能提升了3%以上，较表现最差的OpenMax 算法性能提升了近40%. 在无人机信号数据集上，Open-MUSIC 的Fmeasure 与Accuracy 保持在90%以上，AUC-ROC 在95%以上，性能显著高于其他算法.

综合以上结果来看，Open-MUSIC 相对于其他方法更适合处理电磁数据，比如在无人机数据集上，其性能相较于其他方法至少提升了4%. 同时，Open-MUSIC 更适合处理类数较多且每类样本数较少数据，如在雷达数据集中，每类所含样本最少只有4 个样本. 此时OpenMax 这种依赖每类训练数据的得分来拟合分布的算法效果较差，而Open-MUSIC 使用中心损失训练映射网络，为每个类单独维护一个中心，且子空间分解时每类中心都有相同的权重，在一定程度上可以减小样本数少所带来的影响.Open-MUSIC 在3个数据上的AUCROC 均超过了95%，表明本文算法较其他算法鲁棒性较强，且更适合于电磁数据.

表2 雷达PDW数据集所使用特征映射网络参数表

表5 雷达数据集实验结果

6 结论

本文针对电磁频谱认知领域内的电磁目标开集识别问题，借鉴MUSIC 算法，提出了基于正交子空间分解的开集识别方法Open-MUSIC. 该方法通过使用映射网络得到的已知类特征，组成已知类中心特征矩阵，进而对该矩阵进行正交子空间分解，得到其值域子空间与零域子空间，通过计算测试样本特征在两个子空间内的投影比值来对未知类进行识别，以提升识别效果. 实验表明Open-MUSIC 算法在电磁数据集上效果较其他开集识别算法更好.