计及风力资源的风电场出力研究
2022-07-02曹建伟陈文进沈诚亮张若伊刘皓明
曹建伟,陈文进,沈诚亮,张若伊,张 认,刘皓明
(1.国网浙江省电力有限公司湖州供电公司,浙江 湖州 313000;2.国网浙江省电力有限公司,杭州 310007;3.河海大学,南京 211100)
0 引言
在“双碳”背景下,我国新能源发电得到进一步发展,大规模新能源并网将推动能源清洁低碳转型。新能源发电具有显著的间歇性、随机性与波动性,大规模新能源的集中/分散并网方式增大了电网运行控制难度,同时加大实时电力供需平衡难度[1-3]。
新能源发电受自然资源因素分布的影响,在时间和空间上表现出一定的相关性和聚集性[4]。对新能源进行聚类集群协调控制是解决大规模新能源时空不确定性以及经济调度关键问题的内容之一[5-7]。目前新能源集群划分方法主要有聚类法[8-9]、复杂网络社团发现法[10-11]和智能优化法[12]等3类。文献[8-9]通过建立描述电网节点的电气距离指标,采用聚类算法将电网划分多个区域,实现电网分区协调安全运行。文献[10-11]建立兼顾系统模块度与有功功率平衡度指标,构建提高分布式电源消纳和储能系统经济性的集群储能控制模型,促进新能源消纳。文献[12]通过建立电气距离和有功无功平衡度的综合指标,采用遗传算法划分电气耦合性较强的新能源集群,提升新能源调压能力以及电网的有功平衡度。以上文献通过建立划分指标,构建不同的新能源集群单元,采取群调群控的方式,促进新能源电网安全经济运行。但以上的划分指标是基于新能源运行特性而建立的,没有考虑资源因素对新能源运行特性的影响,而新能源的运行特性与资源因素之间具有关联特性。并且对于采用聚类算法的集群划分,多以计算样本之间距离作为聚类的判断依据,使得聚类结果呈现样本距离相近特征,无法保证新能源出力特性相关性的可靠描述。
另有研究表明,新能源发电的随机波动性可由一系列出力场景进行表征,通过多场景的电力平衡计算是实现中长期发电计划优化和新能源消纳分析的有效方法[13]。目前构建单一新能源场站出力场景主要分为统计预测法[14]和元启发式法[15]。统计预测法如:文献[16-17]考虑风光场站出力互补性,统计分析风光场站历史数据并建立新能源基地出力场景;文献[18]采用FCM(模糊聚类)算法对新能源历史时序出力数据进行聚类分析,生成该聚类典型的出力场景。该类方法在拟合精度、计算效率及算法稳定性方面较难平衡。元启发式法如:文献[15,19]分析多风电场功率在时空尺度上的相关性,采用马尔科夫链模型描述功率曲线的转移,建立强相关风电场群功率曲线随机模型。该类方法的模型状态数通常取决于人工经验,当数据量庞大时,该方法易陷入某一状态不发生转移导致拟合失败。
针对以上研究存在的问题,本文考虑资源相关性对新能源集群聚类可靠性的影响,分析新能源场站资源相关性,建立不同环境条件的新能源差异化出力模型。首先,构建新能源资源与出力特性相结合的特征数据作为新能源场站聚类分析的特征数据,采用改进K-means 算法对新能源场站特征数据进行聚类分析,建立不同资源条件的新能源发电集群。然后对新能源场站历史出力数据进行聚类分析,以不同的聚类中心曲线作为典型出力曲线,构建新能源场站差异化出力模型,以提升出力模型拟合新能源出力特性的精确度。最后以中国东南某地区多个风电场实际监测的资源环境与出力数据,分析计及资源因素的聚类方法对新能源场站相关性的影响,以及建立的新能源场站差异化出力模型拟合实际出力的准确性。
1 新能源场站资源主成分分析
风速、辐照是新能源发电的基础,而温度、湿度、气压、风向、云量等与风速、辐照具有强相关性[20],并且地理位置、地貌对气象因素有一定的影响。因此新能源场站资源数据呈现多维度特点,并且特征数据之间具有相关性,存在信息重叠,这增加了新能源资源分析的复杂度。为分析特征之间相互关联的复杂关系,采用主成分分析法对多变量相关性进行处理。
主成分分析是一种分析多个相互关联变量的观测数据统计方法,通过提取观测数据中的重要信息,将多个特征转化为少数几个能够反映原先特征信息的一组新的正交变量,即为原特征的主成分[21-22]。以下介绍新能源资源主成分提取步骤。
1.1 数据标准化处理
设新能源场站资源观测数据X=[xij]n×m有n个样本m个特征,对各特征数据xij进行标准化处理:

1.2 计算相关系数矩阵R
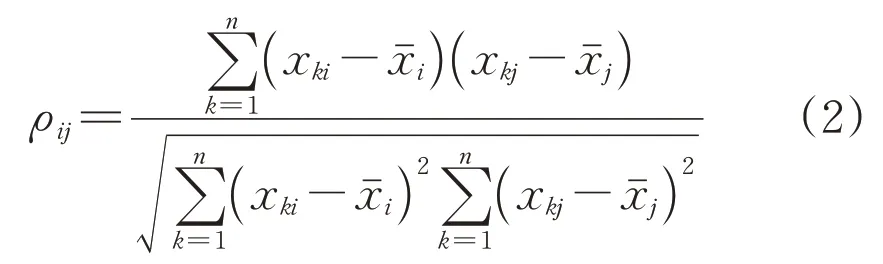
式中:xki和xkj分别为特征i和特征j的第k个样本;和分别为特征i和特征j的平均值。
1.3 计算相关系数矩阵R的特征值和特征向量
对|λE-R|=0 求解,其中E为单位矩阵,计算相关系数矩阵R特征值λi(i=1,2,…,m)并按从大到小进行排序,相应的特征向量μ1,μ2,…,μm,其中μi=(ai1,ai2,...,aim)。主成分可表示为:

式中:fm为第m个主成分;为标准化矩阵第m列向量。因此可由各主成分向量组成一个n×m维的表征新能源场站主要资源信息的主成分矩阵F。
1.4 计算特征值累计贡献率
为简化数据,同时能够包含更多原始信息,通常以累计贡献率al≥0.85作为选择主成分个数的依据。
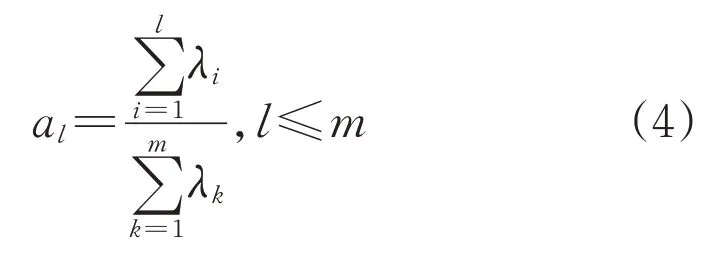
依次对相关系数矩阵特征值计算累计贡献率,当al≥0.85时选取f1,f2,…,fl作为描述原始观测数据矩阵X的主成分,代替原先m个特征:
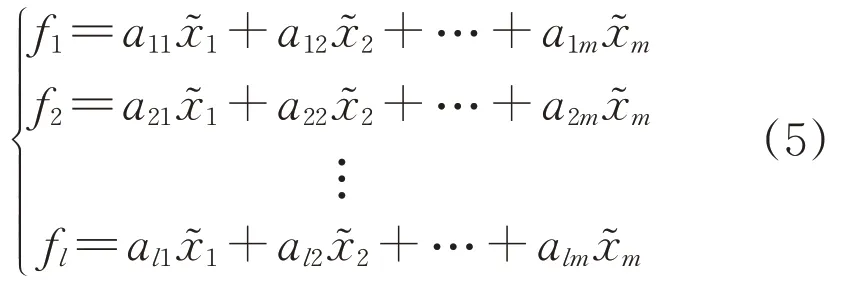
1.5 标准化特征的客观权重
为简化主成分,采用熵权法进行赋权,合理确定指标重要程度[23]。
1)计算特征比重。评价第i个特征的第j个样本的特征比重pij为:

2)计算特征熵值和差异系数:

式中:ej为特征熵值;dj为差异系数,dj越大表示该特征包含的信息量越多,相应的权重越大。
3)计算各特征的熵权:

式中:ωj为第j个特征的权重,组成一个权重向量ω以表征各特征信息权重。
对式(5)采用权重向量替代简化主成分,即:

则gi表示第i个新能源场站资源特征向量:
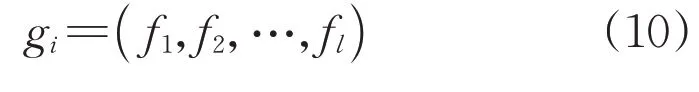
2 新能源场站出力特性指标
考虑风光发电出力的自然特性,本文采用文献[24]给出的新能源出力特性指标,以年利用小时与月平均出力表征新能源场站季运行特性,同时用日平均出力与分段利用小时数表征新能源场站日运行特性。
1)年利用小时数
年利用小时数为新能源年发电电量与装机容量的比值:
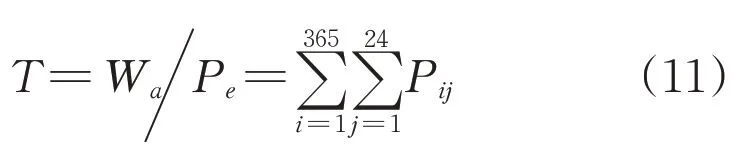
式中:T为年利用小时数;Wa为新能源场站年发电量;Pe为对应的新能源场站装机容量;Pij为第i天j时新能源出力标幺值。
2)月平均出力
以新能源某一月的发电量与当月小时数的比值表示月平均出力:
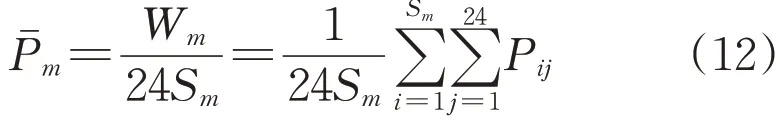
3)日平均出力
计算新能源场站24 h平均出力:
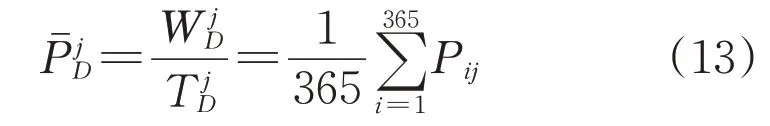
4)分时段利用小时数
计算新能源场站全年24 h各时段利用小时数:

式中:Tj为全年内在j到j+1时段的新能源利用小时数;Wj为全年内在j到j+1 时段的新能源发电量。
年利用小时数与分时段利用小时数满足关系:

通过计算以上新能源场站出力自然特性指标,生成表征新能源场站i的出力特性指标向量pi。
3 计及风力资源的风电场出力分析
3.1 新能源聚类分析
考虑新能源资源在时间和空间上的关联特性,选择新能源场站资源特征向量与新能源场站出力特性指标作为聚类分析的特征数据,建立资源与运行特性均具备相关性的新能源发电集群。
传统K-means算法存在对初始聚类中心敏感、全局搜索能力较差、聚类精度低等问题[25],如初始聚类中心随机选取会导致算法不稳定[23],聚类中心数量取值不合理会增大聚类结果的误差[26]。本文采用基于聚类紧密度和距离原则[27]的改进Kmeans算法对新能源场站进行聚类分析,优化聚类簇数目和初始聚类中心,提升聚类结果的稳定性。
在所有聚类对象中选择密度最大的对象作为初始中心。而对象的密度由其与所有对象的距离中的最大值表示,该值反映对象附近空间的稠密程度,该值越小说明对象的密度越大[2],可将该对象选为初始聚类中心。基于改进K-means 算法新能源聚类的计算步骤如下[27]:
1)输入n个新能源场站相同时间跨度下的资源主成分与出力自然指标集合C:
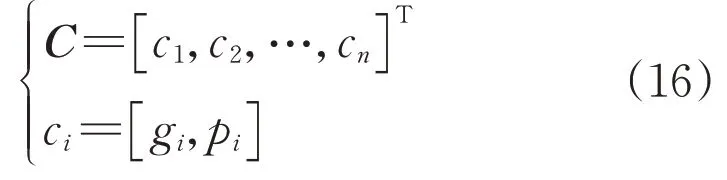
2)计算集合C中各行向量之间的欧氏距离,并存入距离分布矩阵D:
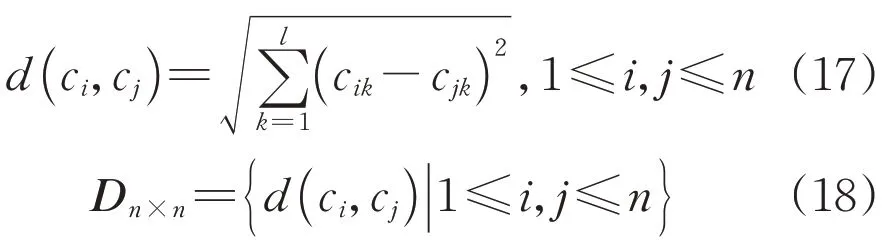
式中:ci和cj为集合C中的任意两个聚类对象;l为向量的元素数目;Dn×n为对角矩阵并且对角线元素均为零。
3)将距离分布矩阵D每一行的距离参数d(ci,cj)存入距离数组Dm:
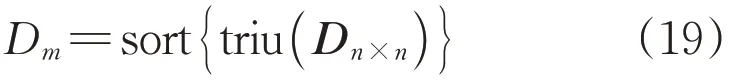
式中:triu(•)表示提取距离分布矩阵Dn×n的上半角元素;sort{•}表示对C中所有对象的欧氏距离进行排序;Dm为存储经排序的距离参数的距离数组,距离数组最小值min(Dm)表示对应密度信息最大的场景,即第一个初始聚类中心y1。
4)基于距离原则选择与初始聚类中心y1距离最大的对象作为第二个初始聚类中心y2。
5)计算未被选择的ci与初始聚类中心y1和y2之间的欧氏距离,并计算与两个聚类中心最小距离的最大值di,对应的对象即为第三个初始聚类中心y3。其中di计算如下:

6)将集合内未被选择为初始聚类中心的对象按最小欧氏距离的原则归属为相应聚类中心的簇类。
7)采用手肘法计算簇内SSE(误差平方和)[28-29],选择最优聚类数目:
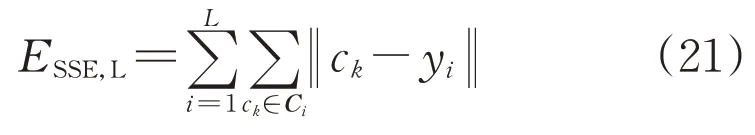
式中:ESSE,L为聚类数目L对应的簇内误差平方和;Ci为第i个簇;ck为Ci的样本;yi为第i类聚类中心。根据不同聚类数目的簇内SSE 折线图,选择折线坡度骤减的点作为最优聚类数目。
8)重复步骤5至步骤7,完成初始聚类中心的选择,对每个初始划分的簇的场景求取均值并作为该簇类新的聚类质心vi:
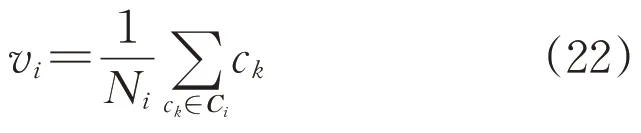
式中:Ci和Ni分别为第i簇的集合与对象数目。
计算集合C中的对象与聚类质心vi的最小距离,将对象更新隶属该簇类:

式中:Di表示以vi为聚类质心的一簇数组。
9)当各簇的聚类质心两次迭代更新的欧氏距离的最大值满足下式则停止迭代:

3.2 差异化出力场景构建
本文首先建立资源相关的新能源发电集群,对集群内各场站历史出力曲线进行聚类分析,避免多场站聚类分析时因聚类曲线数量不同而导致复杂度和计算量增加的问题[24]。
在建立资源相关新能源发电集群后,采用聚类算法对新能源场站一定时间跨度的历史出力曲线进行聚类分析,获得聚类中心表征新能源场站不同运行水平的典型出力曲线,计算分析步骤如图1所示。
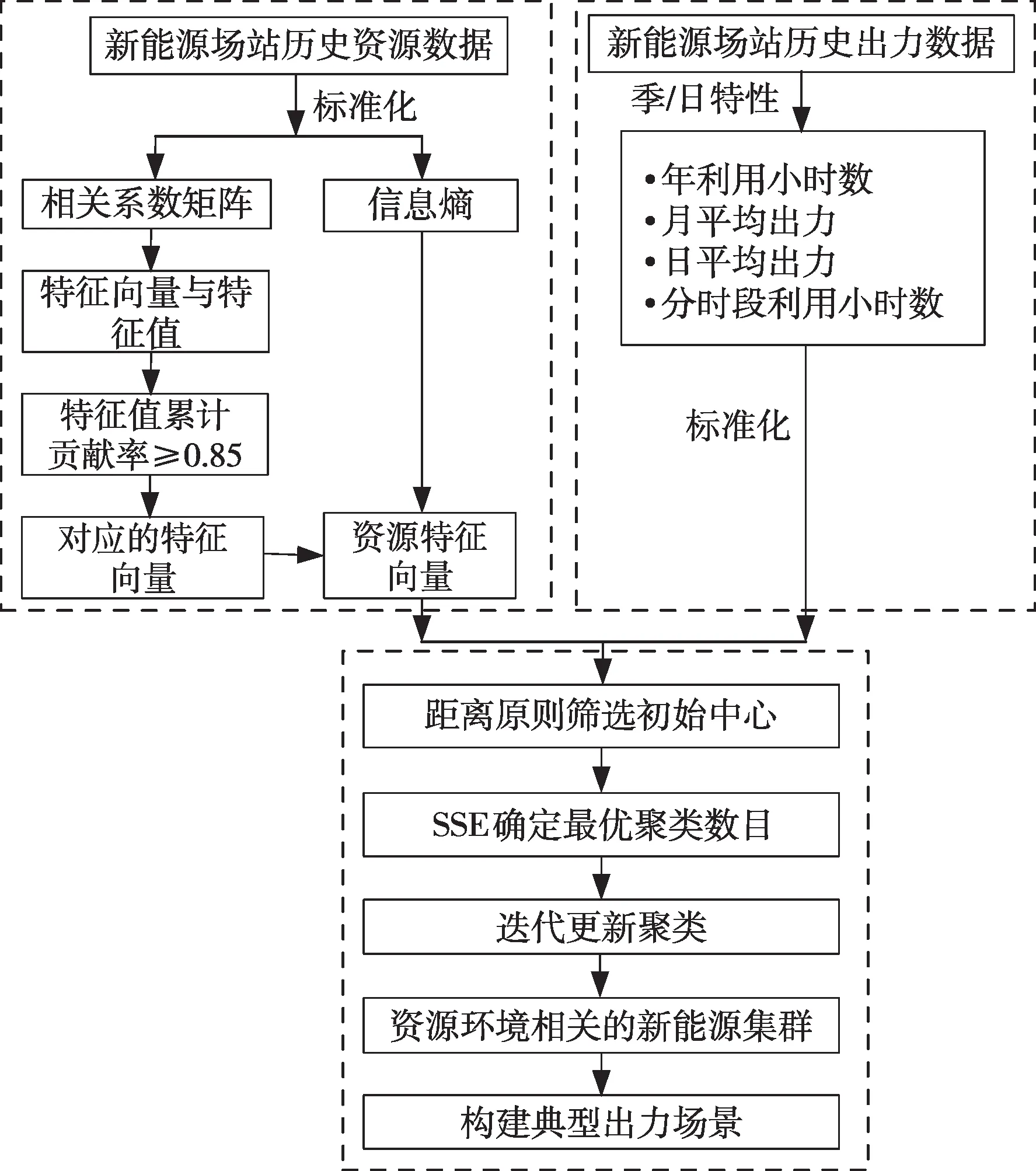
图1 计及风力资源的风电场出力分析流程
4 算例分析
本算例基于中国东南某地区7 个风力发电场,装机容量总计为283.5 MW,选择2018 年夏季的历史资源数据与出力数据,分析该区域新能源资源与出力关联特性,建立不同环境条件下新能源出力特性模型。本文视是否考虑新能源资源因素,分析不同聚类结果的相关性和风电场出力曲线拟合准确度。
4.1 基于新能源场站资源主成分与出力特性指标的聚类分析
风电场提供的资源历史数据有风速、风向、湿度、温度、气压,数据颗粒度为15 min。通过聚类算法分析,获得图2所示不同聚类数目下簇内SSE折线。

图2 不同聚类数目的SSE折线
由图2 可看出,聚类数为3 时折线坡度最大,因此最佳聚类数目为3。对各风电场站进行聚类分析,并采用SSE 以及斯皮尔曼相关系数ρ分析聚类效果和聚类出力曲线之间变化趋势与关联程度[30]。
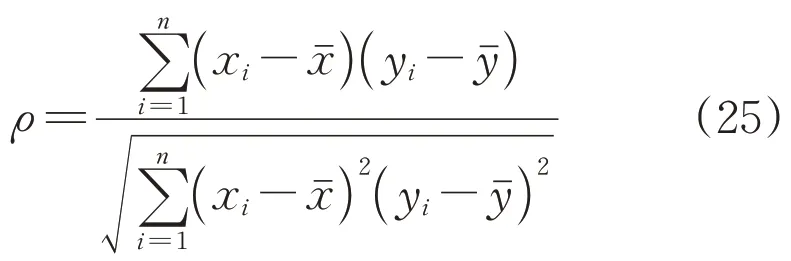
式中:ρ为斯皮尔曼相关系数;和分别为变量x和y的平均值。
由表1 可看出,考虑资源因素的SSE 大于不考虑资源因素的SSE 值,反映出考虑资源相关的新能源集群之间紧密度较疏松。根据各场站历史出力数据计算出典型日出力曲线,分析是否考虑资源因素条件下各风电集群的出力曲线相关性,如图3、图4所示。
分别对图3、图4集群的风电出力曲线计算斯皮尔曼相关系数,得到如表2所示结果。
从图3、图4可以看出,各集群内包含了不同出力水平的风电场站,而不考虑资源因素的聚类结果反映出集群内的出力曲线距离相近,因此表1中考虑资源因素的SSE 大于不考虑资源因素的SSE。但从表2可以看出,考虑资源因素的各集群出力曲线相关性较典型日法得到提升,反映出资源相关性的不同容量场站,其出力曲线变化趋势具有相关性,避免以出力数据作为单一聚类数据的聚类方法对聚类结果相关性的影响。
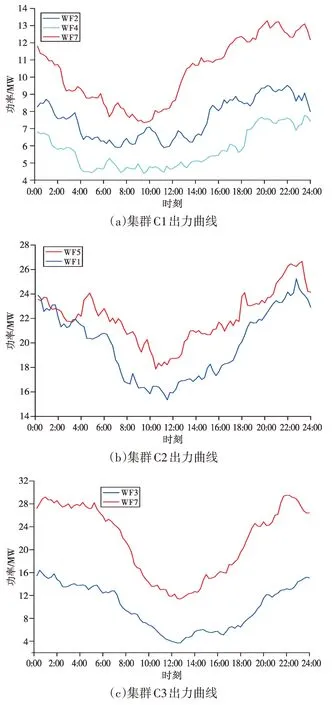
图3 考虑资源因素的风电场夏季典型日出力特性
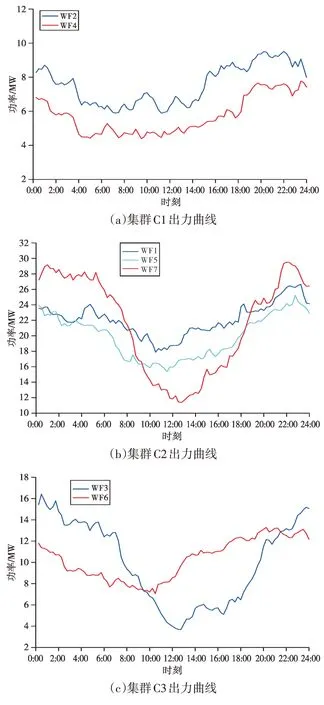
图4 不考虑资源因素的风电场夏季典型日出力特性
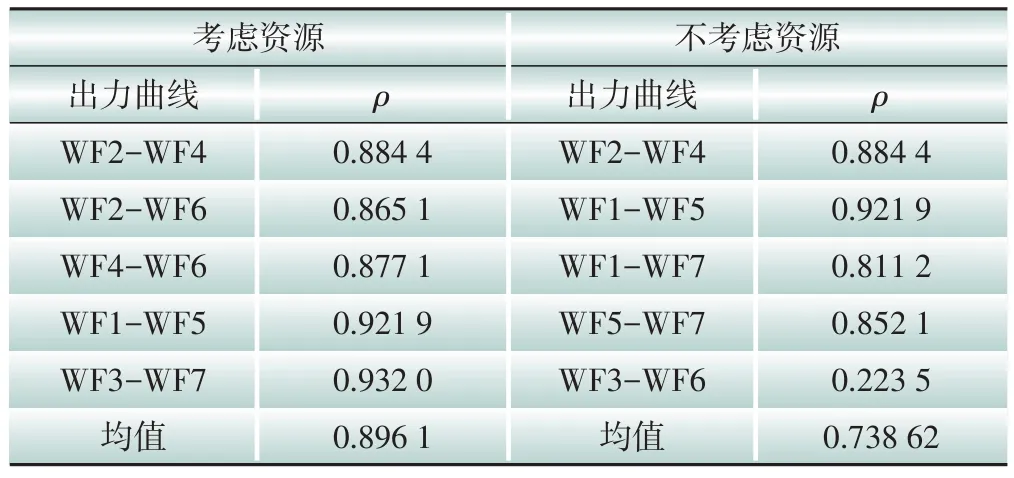
表2 风电出力曲线斯皮尔曼相关系数
4.2 新能源场站差异化出力模型分析
中长期新能源出力场景构建以典型日法[31]和时序仿真法[32]两种方法应用最为广泛。时序仿真法采用新能源出力时间序列数据除以对应周期内新能源总装机容量,将其归一化后来模拟新能源出力时间序列,准确性较高,但计算量大,仿真时间较长[19,33]。本文通过聚类算法计算不同资源环境的风电集群内各风电场的聚类中心,建立表征风电场不同运行水平的典型出力模型。选择典型日法、时序仿真方法与本文方法进行比较分析,其中时序仿真法采用文献[31]方法。图5—7 分别为3个风电集群中各风电场的出力曲线,其中每个出力曲线的百分数表示以该曲线为中心的日出力曲线数量占总数量的百分比。
采用式(26)计算RMSE(均方根误差)来评估出力曲线与实际风电出力曲线的偏差[32],得到表3所示结果。
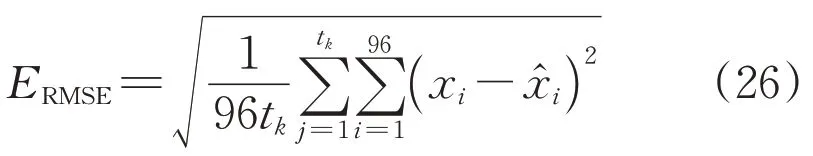
式中:tk为新能源场站第k簇出力样本数量;xi为出力模型中第i时刻的值;为第i时刻实际出力值。
由图5—7 看出,每个新能源集群中的新能源场站有多个不同运行水平的出力曲线,反映出每条出力曲线代表了该新能源场站在不同资源条件下的典型出力曲线。由表3可知,本文建立的风电场站出力模型拟合实际出力曲线的误差水平介于典型日法和时序仿真法之间。但时序仿真法计算量大,仿真时间长,对于大规模新能源场站的集群出力特性分析,其计算效率不高。

表3 出力曲线的RMSE

图5 集群C1各风电场站出力曲线
5 结语
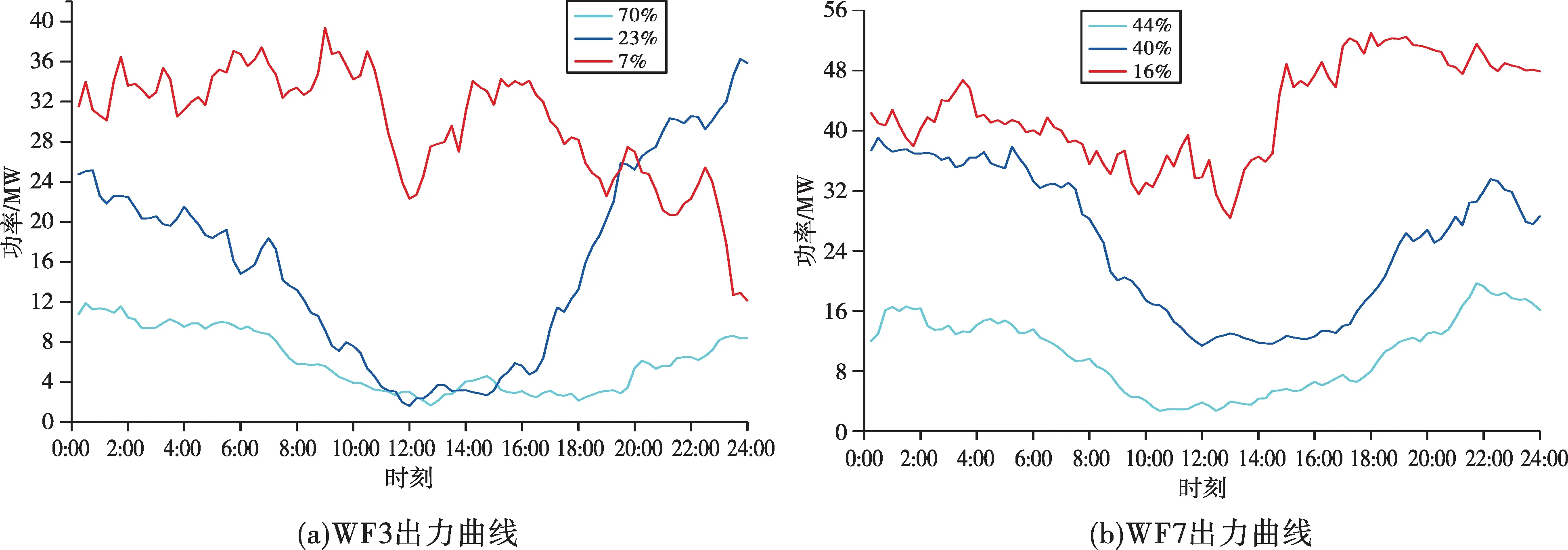
图7 集群C3各风电场站出力曲线
新能源发电受资源环境影响,其出力与资源因素在时间和空间上具有关联特性。本文考虑资源因素构建不同环境条件的新能源差异化出力模型,提高新能源集群划分的相关性以及提升描述出力特性的准确性。
通过对新能源资源特征与出力特性指标的新能源场站特征数据进行聚类划分,克服以出力数据作为单一聚类数据的聚类方法对聚类结果相关性的影响。通过对风电场站日出力曲线聚类,构建新能源差异化出力模型。由出力曲线的RMSE计算结果可知,构建的差异化出力模型在拟合实际出力的误差水平优于典型日法。
本文后续研究将建立新能源差异化模型与不同资源条件的映射模型,根据资源条件选择相应的出力模型,提升新能源预测精度,支撑高比例新能源电网集群协调调控。
