大型中凸变椭圆活塞复杂裙部加工的数据处理研究

赵跃忠

（武汉船舶职业技术学院，湖北武汉 430050）

随着船舶工业的快速发展，为追求船舶动力的高效率、高寿命、低油耗、低噪声等目标，对船舶内燃机的重要零件—活塞的设计和加工精度提出了更高的要求，其中以中凸变椭圆活塞最为常见。这种活塞轮廓形状的特点是：活塞裙部径向横截面近似于椭圆，轴向截面方向的轮廓型线是变化的，有时长短轴方向的椭圆度也会发生变化,属于非圆和非函数曲线，数据处理与运动轨迹合成是关键，尤其是船用大型活塞，不仅具有中凸变椭圆的型面复杂特性，而且其外形尺寸较大，其加工制造成为核心难题。目前通常采用的方法有磨削加工和车削加工两种，其中车削加工多采用靠模法（硬靠模）加工和数控车削（软靠模）加工方式。硬靠模方法借助工装来保证，加工设备具有单一性和加工精度不高的特点；软靠模方法借助数控系统来完成，加工时输入不同的活塞外圆型面数据，设备通用性较好且加工精度较高。

本文论述主要涉及数控车削加工法。下面以φ400mm 大型活塞的中凸变椭圆活塞裙部外圆型面PTC（活塞数控车削系统）机床加工为例，研究大型中凸变椭圆活塞复杂裙部加工时的数据处理过程。

1 中凸变椭圆活塞裙部加工数控原理

中凸变椭圆活塞裙部加工数控机床一般采用PTC 系统，该机床的原理示意图如图1 所示，机床运动由机床主轴（C轴）的回转运动、刀架沿Z轴方向的直线运动、刀架沿X 轴方向的直线运动、刀架上附加的高频直线电机控制的沿U轴方向的直线运动组成，X 轴和U 轴一起控制刀具的切削深度。加工前，将活塞型面数据预先存放在控制计算机的存贮器中；加工时，通过数控车削系统实时联动控制C轴、Z轴、X轴和U轴的运动，实现中凸变椭圆型线轮廓的车削加工。

图1 PTC活塞数控车削系统的椭圆机床原理示意图

2 中凸变椭圆活塞裙部线型的数据处理方法

按照图纸要求将外圆型面按如图2 进行网格化处理。如果网格足够密，即如图中的t 和θ足够小，就可以用这些网格数字点Sx(t,θ)来代表活塞外圆曲面。在加工前，根据图纸要求预先计算出这些网格数字点并将其存放于控制计算机的存贮器中；在车削过程中，利用活塞数控车削系统使刀尖的轨迹准确地通过这些网格点，从而加工出足够精度的活塞。

图2 椭圆机床加工原理

3 φ400mm 大型中凸变椭圆活塞裙部线型的数据处理研究

3.1 φ400mm大型活塞裙部的图形及线型数据

图3为φ400mm 大型活塞中凸变椭圆活塞裙部线型的外形形状两个方向的纵截面外轮廓图：

图3 活塞外轮廓图

φ400mm 大型活塞裙部不同高度上图纸给定的中凸变椭圆活塞裙部线型数据,见表1：

表1 活塞裙部不同高度上长轴、短轴纵向方向图纸给定的椭圆度数据

φ400mm 大型活塞裙部D1、D2 横截面方向图纸给定的各角度半径缩减量数据，见表2：

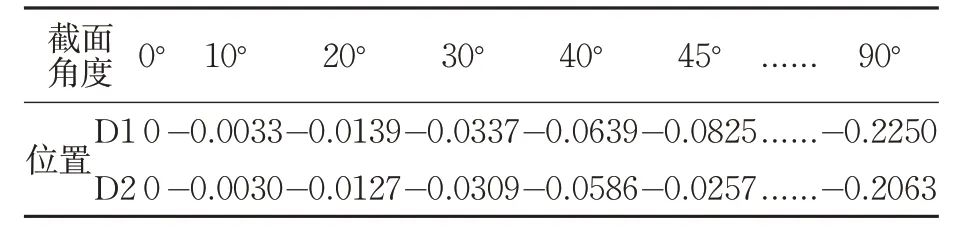
表2 活塞裙部D1、D2横截面方向图纸给定点的各角度半径缩减量数据

φ400mm 大型活塞裙部D3、D4 横截面方向图纸给定的偏心曲线数据，见表3：

表3 活塞裙部横D3、D4截面方向图纸给定的偏心曲线数据

3.2 φ400mm大型活塞裙部线型数据处理与分析

从φ400mm大型活塞给定的数据中可以看出，其活塞裙部形状存在非圆和非函数曲线，线型复杂。根据PTC机床加工的特点，结合活塞的特征，将各截面的数据拟定作如下处理：

3.2.1 活塞裙部不同高度纵向中凸线型的数据处理

活塞裙部不同高度上的中凸线型的数据处理，包括长轴、短轴及各网格角度纵向的线型数据处理，可以直接采用PTC 机床本身自带的最小二乘法的曲线拟合软件，也可用EXCEL表格的曲线程序或CAD 软件中的曲线拟合功能。本文采用PTC软件功能，拟合时将表1中的各截面长轴数据尺寸输入后，可以得到了拟合曲线如下图4所示。

经过数据查证，发现在高度方向42.5～132.1mm 处有凸值，特别是在88.2mm 处达到最凸值，其值为φ399.602mm，大于图纸长轴方向曲线给定的最高值φ399.59mm。比较给定的图纸，处理后的线型数据与图纸要求产生了较大的差异。

为保证图纸给定的纵向截面轮廓线型要求，经过反复测试，最后确定在60mm的位置插入一个特定值φ399.59mm，经过拟合的曲线如图5示。从图可见，经过插入特征点的方式，可以使拟合后的曲线轮廓平滑且符合图纸要求。同时，通过曲线拟合延长的方法，可以得出截面起点高度0mm 处的尺寸数据为φ399.557。

图4 原始拟合曲线

3.2.2 对横截面为一次椭圆的数据进行处理

从表1的数据可以看出，在42.5mm、390mm等处，为标准一次椭圆曲线，计算公式如下：

公式（1）中：Sx(i，j)-半径缩减量；j-活塞裙部横截面高度；i-转角。Ej-在横截面j高度处的一次椭圆度值。

3.2.3 对横截面为二次椭圆的数据进行处理

从表2的数据可以看出，D1、D2截面给定的各角度曲线近似标准二次椭圆曲线，计算公式如下：

公式（2）中：Sx(i，j)-半径缩减量；j-活塞裙部横截面高度；i-转角。Ej、Cj-分别表示在横截面j高度处的一次椭圆度值、二次椭圆系数。

通过公式（2）对表2中D1、D2截面的数据进行处理，得到以下结果：

（1）D1 截面给定的椭圆度值为0.45mm；45°方向的半径缩减量为0.0825mm。代入公式（2）可求出其曲线二次椭圆系数Cj：-0.13333mm。核对D1处的其他角度的半径缩减量，均与图纸相符。

（2）D2 截面给定的椭圆度值为0.4126mm；45°方向的半径缩减量0.0757mm。代入公式（2）可求出其曲线二次椭圆系数：-0.13306mm。核对D2处的其他角度的半径缩减量，均与图纸相符。

3.2.4 对给定的D3、D4 横截面方向的偏心曲线数据处理

对于D3、D4横截面方向图纸给定的偏心曲线数据，如表3所示。由于这两个面为椭圆与偏心相交，需计算出各角度的的椭圆上各点的半径缩减量Sx(i，j)，与该点处的偏心圆上各点对于活塞中心的半径缩减量Rx(i，j)比对，具体见图6 所示，进行如下处理：

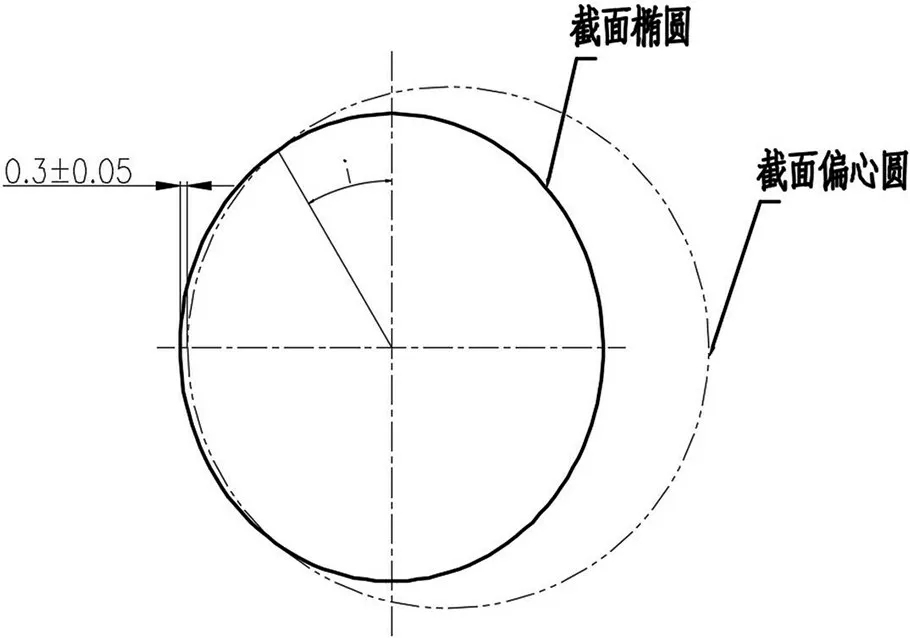
图6 同横截面轮廓曲线上的椭圆与偏心圆比较

（1）Sx(i，j)＜Rx(i，j)时，采用Rx(i，j)值。

（2）Sx(i，j)≥Rx(i，j)时，采用Sx(i，j)值。

完成前四步数据处理后，就可以进行不同截面高度的不同角度上的数据进行理论求解，然后将所有数据进行网格化，如表4。

表4 活塞裙数据汇总表

表4反映了不同截面和不同角度方向的数据，汇总后需进行再一次的最小二乘法曲线拟合修正。如果检查后发现在某一高度或某一角度方向的曲线数据或形状存在问题时，需要根据具体情况进行数据的进一步调整或插补处理，最终的曲线轮廓形状应符合要求且均匀圆滑。

4 结论

大型活塞的中凸变椭圆活塞裙部横截面线轮廓，其形状较为复杂。本文以φ400mm大型活塞为研究对象，应用最小二乘法曲线拟合及一次椭圆、二次椭圆、偏心计算等公式对其进行型面分析，通过建立数学模型，求出活塞裙部各截面相应各点刀具的运动轨迹，并进行数据处理。经我单位所购的PTC 活塞数控车削系统的椭圆机床进行实际加工，获得了较为理想的加工结果。