计算梁弯曲变形的一种特殊叠加法1)

雷芳明 顾春龙 赵永刚

(兰州理工大学理学院，兰州 730050)

梁作为工程领域的基本结构单元，其变形特征备受关注[1-4]。在材料力学中，对梁的弯曲变形计算通常有两种方法，一是积分法，二是叠加法[5-6]。积分法是基于梁的挠曲线近似微分方程的积分计算，通过边界条件和光滑连续条件确定积分常数，进而可得梁的挠曲线方程和转角方程，但对于弯矩为分段函数的梁计算比较繁琐。叠加法则需要记住基本形式静定梁在几种常见载荷作用下的最大挠度和转角，通过直接叠加法或分段刚化法可以计算一般梁在特殊截面上的挠度和转角。而对于较为复杂的情况，比如简支梁抗弯刚度分段刚化为常数、所求挠度或转角不在特定截面、主动载荷作用位置发生变化的情形下，叠加法就比较困难。

本文给出一种基于悬臂梁基本变形的叠加法，该方法在求解简支梁和外伸梁特定截面的弯曲变形时非常有效。

1 理论分析

材料力学中给出的在小变形情况下梁发生弯曲变形时曲率半径与弯矩的关系为[5]

其中，ρ为梁弯曲变形时中性层的曲率半径，M为横截面上的弯矩，EI为梁的抗弯刚度。从式（1）可见，对于两个长度相同、抗弯刚度相同的梁，只要各截面上的弯矩相同，弯曲变形时轴线就会具有相同的曲率，即弯曲程度相同，则整个梁的挠曲线形状亦相同。

梁小挠度弯曲变形时的挠曲线近似微分方程为

其中w为挠度。通过对式（2）积分，并通过位移条件确定相关积分常数，可解得梁弯曲变形的转角方程和挠度方程，这种方法即为积分法。

如图1(a)所示的等截面悬臂梁长为l，自由端B处受集中力F作用，则其弯矩方程为M1(x)=F(x−l) ，将其代入式（2）积分两次，并通过边界条件w1(0)=0 和确定积分常数，可得其挠曲线方程为

图1 悬臂梁在右端受集中力作用

图2所示为长l的等截面简支梁，在左端受集中力偶Me=Fl作用，该简支梁的弯矩方程为M2(x)= ，这个弯矩方程与图1(a)所述受集中载荷作用悬臂梁的弯矩方程完全相同。根据前面的分析，由于上述两种梁刚度相同，弯矩方程亦相同，则它们的挠曲线具有相同的形状。可以通过把一种支撑条件下的挠曲线方程刚性移动和转动得到另一种支撑条件下的挠曲线方程。比如将图1(a)所示悬臂梁的挠曲线方程进行一个转动和刚性移动，即叠加一个线性函数

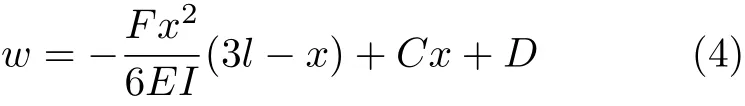
式中，线性项Cx代表挠曲线的转动，常数D代表挠曲线的刚性平移。令式（4）满足简支梁的边界条件w(0)=w(l)=0 ，可得（在这里只有绕A点的转动，没有刚性平移，如图1(b)所示），将C和D代入式（4），得到经过转动的悬臂梁的挠曲线方程为

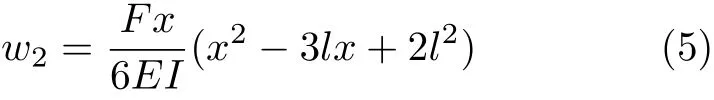
而这正是由积分法得出的图2所示简支梁挠曲线方程的解析解[6]。

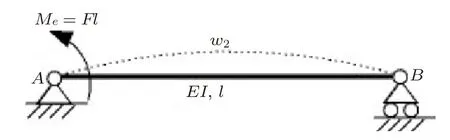
图2 简支梁在左端受集中力偶作用

由上述分析可知，在求解一个梁弯曲变形问题时，可以先计算具有相同弯矩方程的其他基本形式静定梁的变形（其基本变形一般已知），再通过刚性转动和平移求得所关注截面的挠度和转角。在下面的应用举例中，以静定悬臂梁为基本单元，通过悬臂梁的组合叠加出简支梁或者外伸梁（对应的梁段必须具有相同的弯矩方程，组合处满足位移连续条件），再通过把悬臂梁组合结构的挠曲线刚性转动和平移使其满足原结构的位移边界条件，进而计算出所关注的某个截面的转角和挠度。这种方法被称为“特殊叠加法”，该方法在计算简支梁和外伸梁的变形时尤为方便。

2 特殊叠加法的应用

2.1 简支梁非中点的变形计算

图3所示简支梁，在C处受集中力F作用，求D处的挠度和转角。首先求得A和B处支座反力分别为FA=F/3 ，FB=2F/3 ，然后选取在D处固定两个悬臂梁，将两端的约束力作为外载荷作用在悬臂梁上，原主动载荷不变，则悬臂梁组合结构和原来的简支梁具有相同的弯矩方程，其挠曲线A′DB′如图4所示，两端挠度可由叠加法中梁在简单载荷作用下的变形表[6]查到或简单计算出，即

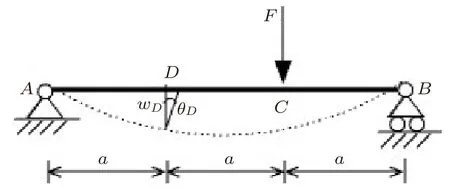
图3 简支梁受集中力作用

图4 等效悬臂梁示意图

因为图3和图4所示结构具有相同的刚度和弯矩方程，因此它们的挠曲线也有相同的形状。将图4中挠曲线两端的挠度移动为零（即将图中所示直线A′B′平移至与AB重合，相应的挠曲线也随之刚性移转），就得到了图3所示原简支梁的挠曲线。图3所示结构D处的挠度和转角亦可由图4中的挠曲线刚性移转而得到，分别为

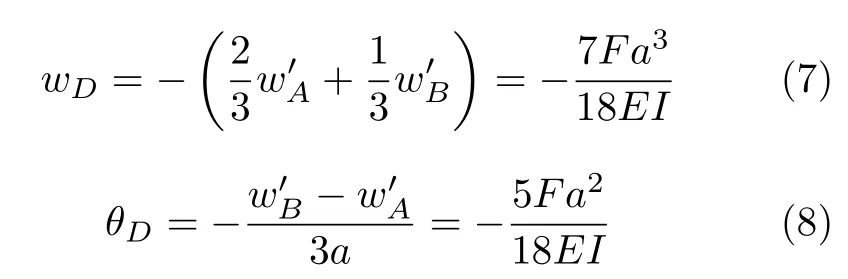
这与教科书中基于积分法得出的结果完全一致[6]。

2.2 阶梯变截面梁的计算

图5所示阶梯变截面简支梁，抗弯刚度分别为2EI和EI，中点C处承受集中力F的作用，求中点的挠度和转角。首先求得两端的约束力均为F/2 ，然后在中点C处固定两个悬臂梁（与原简支梁具有相同的刚度和弯矩方程，因此亦具有相同的挠曲线形状），其挠曲线如图6所示，两端挠度为

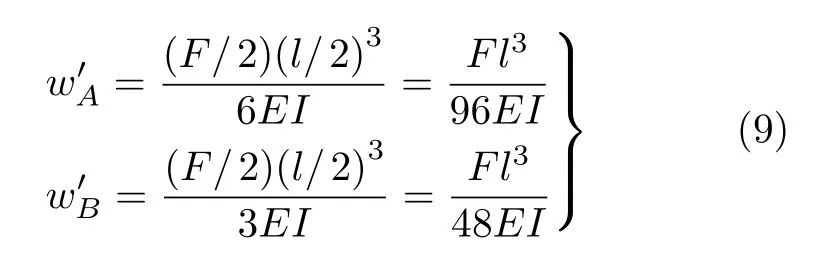
同理，把其挠曲线两端的挠度移转为零（即将图6中所示直线A′B′平移至与AB重合，相应的挠曲线也随之刚性移转），便得到图5所示原变截面简支梁的挠曲线，图5所示结构C处的挠度和转角亦可由图6中的挠曲线刚性移转而得到，分别为

图5 变刚度简支梁示意图

图6 等效悬臂梁示意图

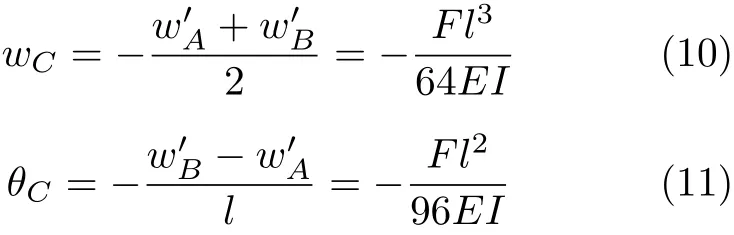
支座A和B处的转角可由θA=θA′+θC和θB=θB′+θC求得。

通过上面的两个计算实例分析，可以看出简支梁需要计算哪个截面的挠度和转角，只需把它变成固定端为该截面的两个等弯矩的悬臂梁，为了保持光滑连续性条件，这两个悬臂梁为同一个固定端（就是欲求位移的截面处）。同时将原来两端的支座反力作为外载荷作用于悬臂梁（以确保具有相同的弯矩方程）。再通过传统的叠加法计算两个悬臂梁两端的变形，最后通过刚性移转使得问题满足原结构的边界条件，便可计算出该截面的挠度和转角。

2.3 外伸梁的变形计算

图7所示外伸梁，CD段受均布载荷q作用，求D处的挠度和转角。首先求得A处支座反力FA=0 ，然后在支座B处固定两个具有相同弯矩方程的悬臂梁，如图8所示，因为图7所示外伸梁与图8所示等效悬臂梁结构具有相同的刚度和弯矩方程，因此二者亦具有相同的挠曲线形状。等效悬臂梁结构的挠曲线为图8中的A′BD′，则两端挠度分别为

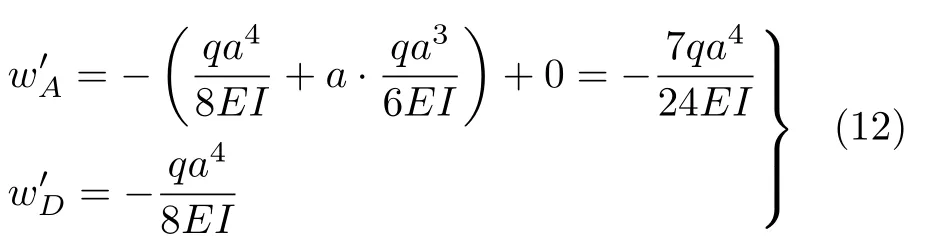
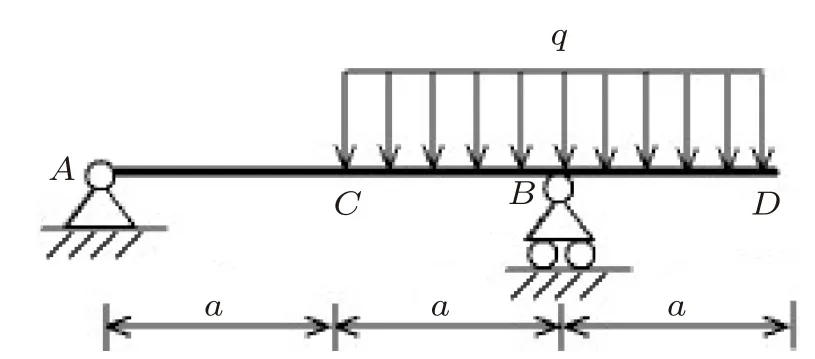
图7 受均布载荷作用外伸梁示意图

图8 等效悬臂梁示意图

D处的转角为

为了让等效悬臂梁的挠曲线满足外伸梁的边界条件，将直线A′B绕B点旋转至与AB重合（相应的挠曲线A′BD′也随之刚性转动，这样A点便满足了外伸梁的边界条件），从而便得到了图7所示受均布载荷作用外伸梁的挠曲线。则图7中D处的挠度和转角分别为

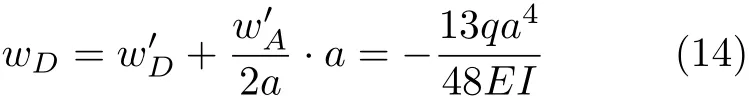
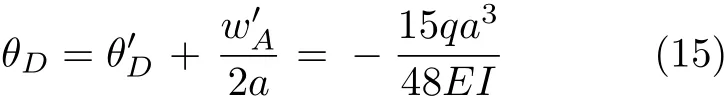
经积分法检验，结果正确。

通过外伸梁变形的计算实例分析，可以看出外伸梁需要在靠近外伸端的支座处将其变成两个与原结构等弯矩的悬臂梁。为了保持光滑连续性条件，这两个悬臂梁为同一个固定端（该固定端为靠近外伸端的支座处，如本例中为B处）。同时将另一端的支座反力作为外载荷作用于所对应的悬臂梁（以确保具有相同的弯矩方程），再通过传统的叠加法计算两个悬臂梁两端的变形，最后通过刚性转动使得满足原问题的边界条件，从而得到原问题的挠曲线形状和所求截面的弯曲变形。

3 结束语

本文基于梁的弯曲变形理论，给出一种求解简支梁和外伸梁弯曲变形的“特殊叠加法”。该方法以悬臂梁的弯曲变形为基础，将简支梁或外伸梁分解为两个悬臂梁的基本变形，再根据光滑连续性条件，将左右两个悬臂梁组装成简支梁或外伸梁，然后通过对挠曲线的转动和平移，从而计算出某个截面的弯曲变形。该方法是对材料力学弯曲变形叠加法的进一步延拓和补充，对求解某些较为复杂的弯曲变形问题非常有效和便捷，同时该方法还可进一步用于求解弯曲超静定问题。