某地铁线路盾构隧道管片裂缝受力与变形分析
2022-07-01黎智
黎 智
(深圳市光明区建筑工务署 深圳 518000)
0 引言
盾构隧道在建设过程中受盾构姿态和管片姿态之间的偏差、管片安装速度、封顶块安装等因素影响,会出现渗漏水、结构裂缝及损坏、管片错台等病害[1-2]。其中,衬砌裂缝是隧道的主要病害形式,裂缝的存在会降低衬砌截面的极限承载力,并且对衬砌的刚度存在一定的影响,容易引起结构的内力重分布[3-4]。基于此,学者们针对盾构隧道复合式衬砌展开了大量研究。LEI 等人[5]通过模型试验研究了浅埋隧道在不同偏压角的非对称荷载作用下,隧道结构和围岩中的应力分布和变化规律以及衬砌破坏的过程;林楠等人[6]通过建立盾构隧道管片三维有限元模型,对盾构隧道病害演化发展机理进行分析。孟祥筝[7]以长沙某深基坑工程为背景,研究不同施工阶段过程中邻近地铁区间的土体位移和管片变形的发展规律。针对盾构管片裂缝成因及治理方面,一些学者做了相应研究。凌同华等人[8]分析了对衬砌结构16 点位和2 点位背后存在空洞时衬砌结构空间受力特征及对裂缝形成的影响。王彦峰等人[9]以广州地区内径为5.4 m的高压电缆盾构隧道为依托,通过建立三维精细化单环电缆隧道有限元模型,研究地表单调超载和超载再卸载情况下的隧道整体变形、椭圆度、接头张开量和螺栓应力的变化情况。
既有研究成果多是针对管片结构的裂损调研、成因分析及治理措施,针对已开裂管片的损伤破坏模式的研究较少。因此,本文以某地区已建成盾构隧道为研究对象,运用MIDAS GTS NX有限元分析软件,采用荷载—结构法,建立衬砌环未开裂与开裂后的二维及三维数值模型,通过改变管片裂缝间的环向刚度及裂缝长度,对衬砌结构受力变形进行计算,并对隧道带裂缝工作情况下衬砌结构受力进行对比分析,为盾构管片开裂后力学性能分析与安全性能评估提供参考。
1 工程概况
某地区地铁盾构隧道管片外直径6.2 m,内直径5.4 m,厚30 cm,宽1.2 m。分块数为6,标准块圆心角72°,两邻接块圆心角64.5°,封顶块圆心角15°,横向接头为2 处,纵向接头为3 处,纵向连接曲螺栓为M24,为错缝拼装。常规检查中,在盾构隧道X环与Y环分别发现两条裂缝,X环与Y环之间间隔7 环管片。其中X环裂缝最大宽度为2.76 mm,Y环为2.67 mm;裂缝深度分别为67.5 mm 和84.1 mm。均发生在管片顶端,其中X环为贯通裂缝。
2 数值分析
2.1 模型假设与简化
采用MIDAS GTS NX 软件对X环及Y环进行数值模拟,计算模型将同一层土体假定为均质、各向同性,土体与结构之间假设变形协调。衬砌结构用三维实体单元模拟,钢筋采用植入式桁架单元,地层与管片之间的相互作用采用地基弹簧单元,弹簧设置为仅受压。地基与管片之间采用弹性连接,弹簧长度取值为1 m。
以垂直洞身方向为X轴,以盾构洞身方向为Y轴,竖直方向为Z轴建立三维模型计算分析,为消除模型边界效应,X轴方向取120 m,Y轴方向取30 m,Z轴方向取133 m(Z轴取值已考虑盾构隧道埋置深度)。方案模型计算采用10节点四面体单元,共划分单元529 021个,节点146 891个。管片及弹簧单元示意图如图1所示,X环与Y环裂缝网格见图2所示。

图1 管片及弹簧单元示意图Fig.1 Schematic Diagram of Segment and Spring Unit

图2 X环与Y环裂缝网格示意图Fig.2 Diagram of Crack Grid of X Ring and Y Ring
2.2 确定计算参数
2.2.1 衬砌结构受主要荷载计算
该段隧道处于Ⅳ级围岩中,埋深93.44 m,物理力学指标如下:管片材料C50,容重为24.5 kN∕m3,弹性模量为34.5 GPa。泊松比为0.2。围岩参数如下:围岩级别为Ⅳ级,弹性抗力系数为350 MPa∕m,泊松比为0.325,内摩擦角为33°,容重为21.5 kN∕m3。
在现行设计中,衬砌设计考虑了下列荷载:①主要荷载(必须经常考虑的荷载):竖向与水平土压力、水压力、自重(静载)、超载重和地基反力;②次要荷载(必要时考虑的荷载)、内部荷载、施工期荷载和地震效应;③特殊荷载:相邻隧道和地基沉陷的影响引起的荷载以及其他荷载[9]。考虑隧道所处区域,本文只考虑主要荷载的作用,计算得到衬砌结构外壁土压力及水压力分布及大小,如图3所示。
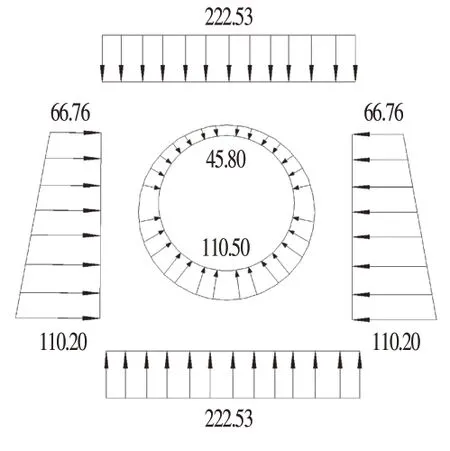
图3 带裂缝衬砌结构受力Fig.3 Force of Cracked Lining Structure (kPa)
2.2.2 确定接头与裂缝刚度及其它参数
将管片接头存在对衬砌环的影响离散为一系列由剪切弹簧和法向弹簧组成的组合弹簧;裂缝的影响采用非线性介质力学数值分析的古德曼(GOODMAN)单元[10]。裂缝界面处古德曼(GOODMAN)单元在三维空间与接触单元类似,在确定外荷载作用下满足式关系,单元的3 个参数法向刚度KN、切向刚度KS及转动刚度Kθ,这三个刚度采用下式计算:
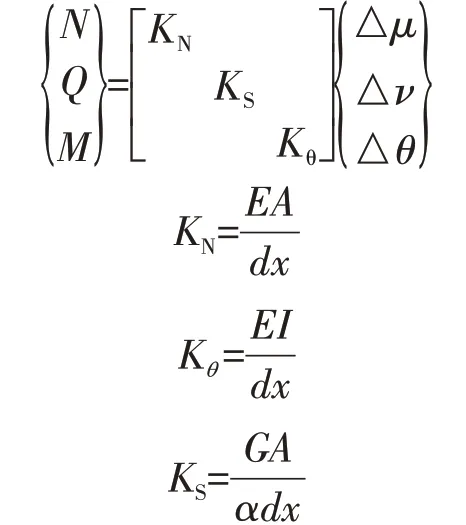
式中:N、Q、M分别为不考虑裂缝影响的轴力、剪力、弯矩;△μ、△ν、△θ分别为轴向变形、剪切变形、相对转角位移;E为混凝土弹性模量;G为混凝土剪切弹性模量;α为应力分布不均匀的改正系数,对矩形截面采用1.2;A为裂缝截面有效面积;I为裂缝截面有效惯性矩;dx为裂缝有效宽度。
采用荷载-结构法建立隧道结构模型。计算模型中地层弹簧刚度为15 000 kN∕m3,混凝土弹性模量E=3.45×107kPa,管片刚度分别取KsX=8.25×105kN∕m,KsY=1.03×106kN∕m,KNX=2.33×106kN∕m,KNY=2.90×106kN∕m。管片间纵缝接头的剪切刚度取8.0×104kPa∕m,环缝接头的剪切刚度取6.5×104kPa∕m。
2.3 计算结果与分析
利用荷载-结构法分析正常管片和带裂缝管片(X环和Y环)在本工程盾构隧道埋深位置所受力及变形,如表1 所示,内力与变形云图如图4~图7(限于篇幅,再加上X环与Y环裂缝管片云图相近,本文只列出了正常管片与X环裂缝管片的内力与变形云图)。
由表1 可知,正常管片承受竖向荷载以及左右侧向压力后,管片自身发生一定变形,水平向呈现外扩趋势,左右拱腰位置为变形最大值,左侧向外2.72 mm,右侧向外2.47 mm,如图4⒜所示;而竖向拱顶发生下沉,最大值为8.25 mm,如图4⒝所示。管片承受弯矩最大值为357 kN·m,位于拱顶,如图5⒜所示;承受轴力最大值为1 241.50 kN,位于拱顶,如图5⒝所示。
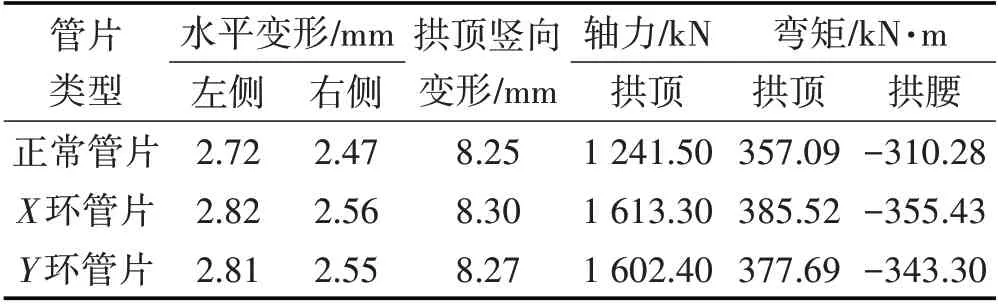
表1 正常管片和带裂缝管片的内力与变形Tab.1 Internal Force and Deformation of Normal Segment and Segment With Crack
由表1和图4~图7可知,利用荷载-结构法对正常管片、X环管片(裂缝管片)及Y环管片(裂缝管片)受力及变形进行建模计算,计算结果表明:
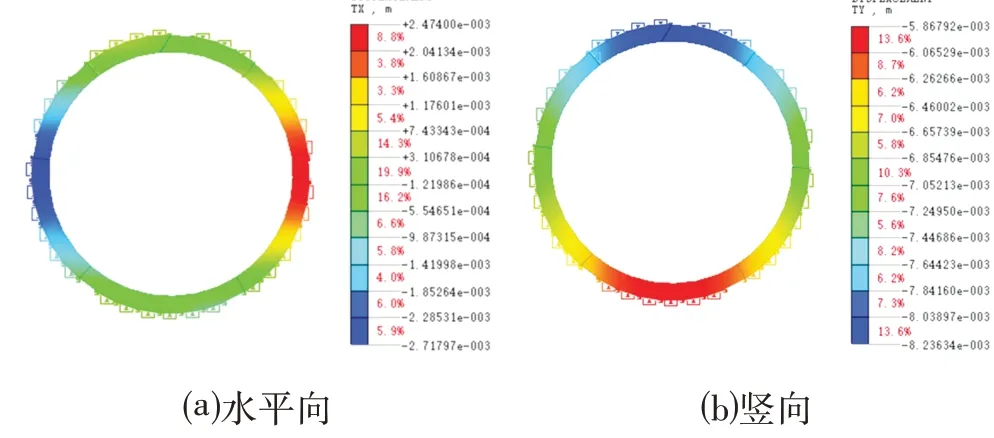
图4 正常管片变形Fig.4 Deformation of Normal Segment
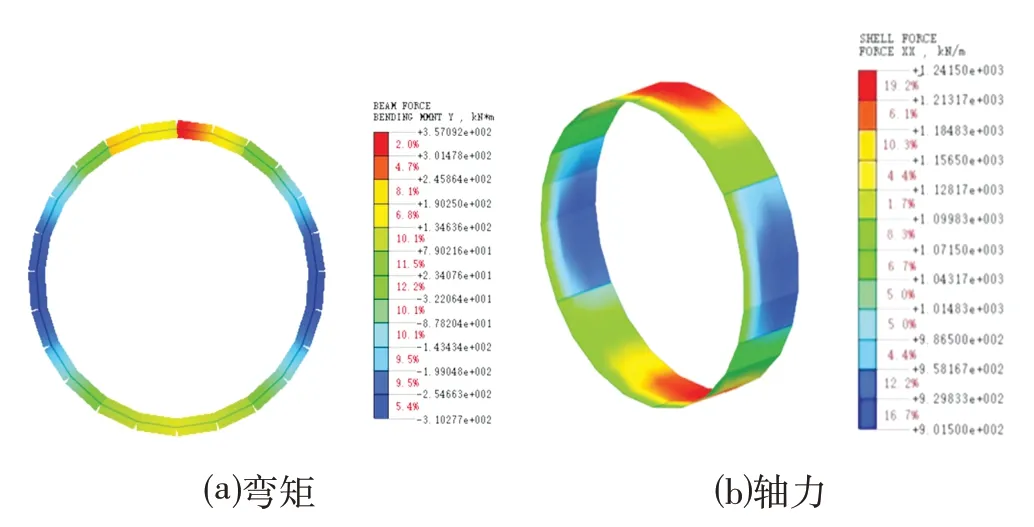
图5 正常管片弯矩及轴力Fig.5 Bending Moment and Axial of Normal Segment
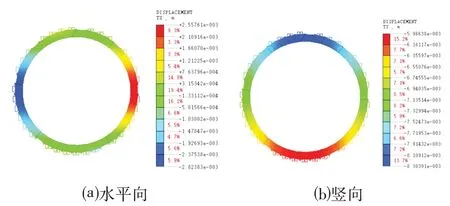
图6 X环管片变形Fig.6 Deformation of X Segment
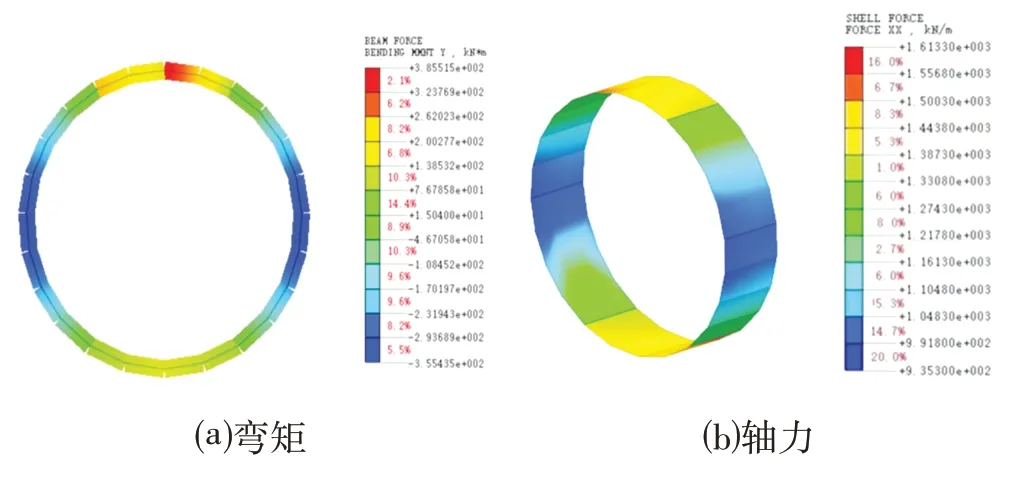
图7 X环管片弯矩及轴力Fig.7 Bending Moment and Axial of X Segment
⑴X环管片在拱腰处水平变形较正常管片外扩0.10 mm,如图4⒜与图6⒜所示;最大竖向变形在拱顶处较正常管片增大0.05 mm,如图4⒝与图6⒝所示;在拱顶位置的弯矩较正常管片增大28.43 kN·m,在拱腰位置增大45.15 kN·m,如图5⒜与图7⒜所示;在拱顶位置的轴力较正常管片增大371.8 kN,如图5⒝与图7⒝所示;由此可见,X环裂缝管片在拱顶处较正常管片产生了应力集中。
⑵Y环开裂管片在拱腰处水平变形较正常管片外扩0.09 mm,最大竖向变形在拱顶处较正常管片增大0.02 mm,在拱顶位置的轴力较正常管片增大360.9 kN,在拱顶位置的弯矩较正常管片增大20.6 kN·m,在拱腰位置增大33.02 kN·m;由此可见,Y环裂缝管片在拱顶处较正常管片产生了应力集中。
3 结论
对盾构隧道开裂与未开裂环片进行数值计算,通过分析可得到如下结论:
⑴ 利用古德曼(GOODMAN)单元来模拟裂缝建立的三维非线性有限元计算模型可以较为真实地反映隧道结构的受力状态,表明该模型在合理的参数下有效,可作为衬砌结构开裂后力学性能分析手段。
⑵通过对比管片有无裂缝的受力和变形分析,管片在带裂缝状态下剪力、弯矩、位移均比正常管片大。经过分析,该两处裂缝对结构总体承载能力影响较小,且影响范围在裂缝周围小区域内。由计算可知,该两处裂缝尚未成为结构性裂缝,但在拱顶处较正常管片产生了应力集中。
⑶经过有限元模拟分析管片裂缝对隧道结构受力和变形的影响还与裂缝数量、长度、深度、宽度等因素密切相关,该问题将在今后进一步的深入研究。
