地铁深基坑等效地连墙受力变形机理数值模拟研究
2022-07-01田毛进常延峰龙良宇张腾奔焦亚龙
田毛进,常延峰,龙良宇,张腾奔,焦亚龙
(中铁广州工程局集团深圳工程有限公司 广州 511457)
0 绪论
随着城市化建设的推进,地下空间开发规模不断发展壮大,地铁车站是解决城市交通问题的重要方式。在城市中进行地铁车站的施工,对基坑位移及周边建筑的沉降等条件的要求较为严格。同时,在繁华地段,在高压线路等低净空条件下,难以进行地铁深基坑地连墙的施工,影响施工进度。广州市某地铁车站,在低净空条件下,采用多段圆形钢筋笼进行分节吊装施工,取代传统地连墙钢筋笼,形成等效地连墙。目前,仍未见有学者进行等效地连墙的研究,而在传统地连墙受力机理分析方面已较为成熟。孙长军等人[1]依托北京地铁14 号线某车站进行地连墙受力变形研究,结合实测数据,揭示了地连墙的受力变形规律;杨永文[2]采用有限元方法进行软土地区排桩墙与T型地连墙的数值分析,提出优化设计方案,通过实测数据对比,验证了优化方案的有效性;秦会来等人[3]采用ABAQUS 建立超深地连墙数值模型,模拟分析不同施工阶段下墙体的变形及对周边土体的影响;李炜明等人[4]基于监测数据进行异形基坑地连墙的受力研究,并总结其变形分布规律;胡坚尉[5]采用有限元法方法建立预制预应力地连墙数值模型,对比分析普通地连墙、先张法与后张法三种模型的受力变形规律,得出后张法能够有效控制控制变形的结论,为该方法的推广提供理论支撑;孟小伟[6]结合北京某地铁工程的基坑实测数据,分析总结了地连墙墙顶变形分布规律;黄卫根等人[7]结合深圳地铁某车站的施工监测数据,采用最小二乘法进行数据拟合,对地连墙弯矩数据进行反分析与安全评估;赵宇等人[8]采用MIDAS 建立狭长深基坑数值模型,模拟分析软弱地层条件下深基坑的变形规律;唐福源等人[9]采用FLAC3D进行深基坑支护参数的研究分析;李永华等人[10]采用能量法进行深基坑内支撑构件的稳定分析。
本文基于上述研究,采用MIDAS进行等效地连墙受力变形数值研究,分析对比不同施工工况下传统地连墙与等效地连墙的受力机理及变形规律,验证等效地连墙的有效性,为等效地连墙的工程应用提供理论支撑。
1 等效地连墙原理及受力机理研究
1.1 等效地连墙原理
在低净空条件下,地铁车站深基坑地连墙成槽采用冲击钻打孔,2台冲击钻机交替打孔,最后采取方捶修孔,孔与孔之间相连接形成一个槽段。根据工程造价、地层地质条件及机械适用性等方面考虑,冲击钻机成孔完全满足要求。
地连墙的钢筋笼采用多段圆柱形钢筋笼,形成等效地连墙(见图1),在低净空的特殊情况下,采用普通吊机进行分节吊装施工。吊装施工过程中,分布式光纤传感器采用边吊装边布置的方法进行,用于监测等效地连墙的应变变形情况。
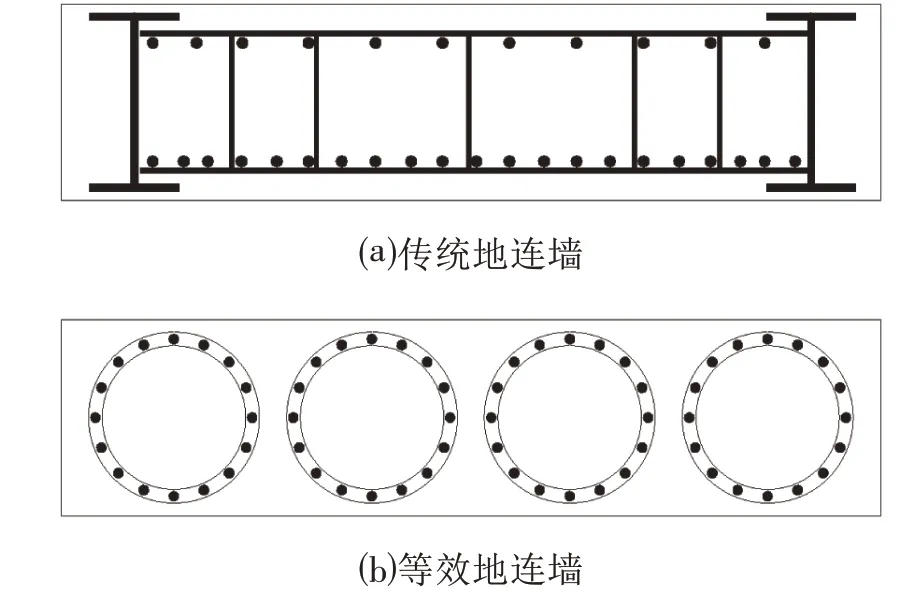
图1 等效地连墙原理Fig.1 Schematic of Equivalent Ground Connecting Wall
1.2 单幅等效地连墙受力机理研究
采用MIDAS 分别建立传统地连墙模型和等效地连墙模型,如图2 所示,在底部施加固端约束,模型顶端Y轴方向水平线上施加合力为-1 000 kN的荷载,进行模型变形研究,初步分析等效地连墙及钢筋笼的变形规律。

图2 单幅地连墙模型Fig.2 Single Wall Model
地连墙与钢筋笼位移云图如图3、图4 所示,可知方形笼最大位移为-0.923 m,圆形笼最大位移为-0.323 07 m,在相同的受力条件下,圆形钢筋笼相同位置的钢筋变形小于方形钢筋笼,这是由于圆形钢筋笼的配筋强度较方形钢筋强,保证等效地连墙的安全性。单幅地连墙的变形规律基本一致,其中,采用圆形钢筋笼配筋的地连墙强度高于传统地连墙。因此,在低净空条件下,等效地连墙的配筋方式能够满足强度要求。

图3 钢筋笼位移云图Fig.3 Cloud Diagram of Reinforcement Cage Displacement
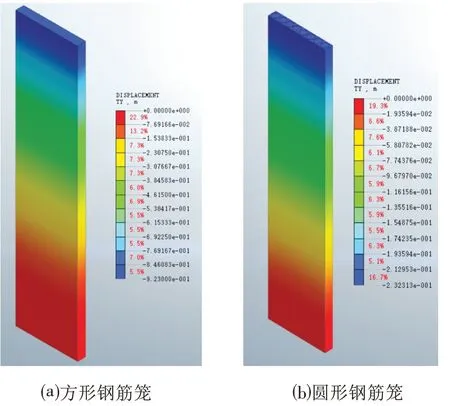
图4 地连墙位移云图Fig.4 Displacement Nephogram of Diaphragm Wall
2 深基坑等效地连墙受力变形机理数值分析研究
2.1 深基坑数值模型建立
2.1.1 定义材料属性
根据深井站工程项目土层参数定义有限元模型的材料属性,土层参数如表1与表2所示。
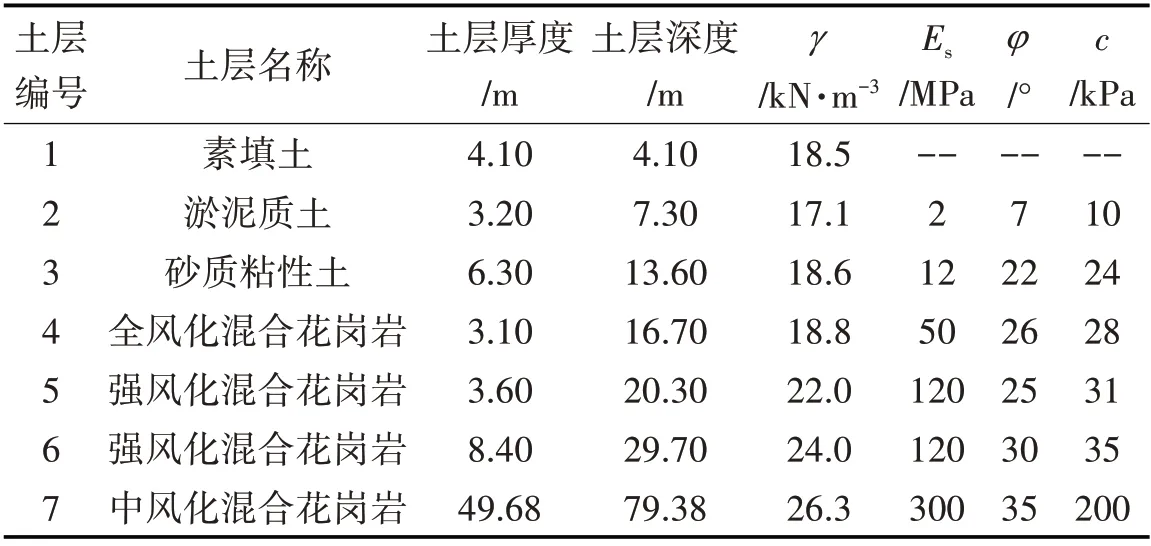
表1 土层材料的各项力学性能参数Tab.1 Mechanical Property Parameters of Soil Layer Materials
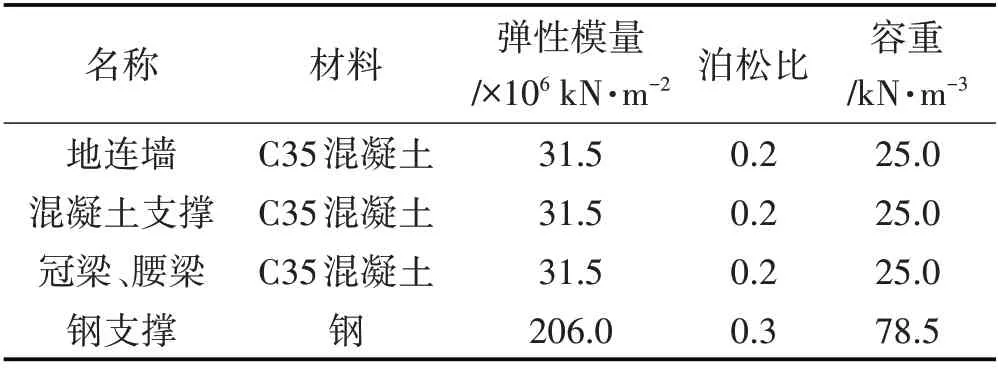
表2 土层材料的各项力学性能参数Tab.2 Mechanical Property Parameters of Soil Layer Materials
2.1.2 建立几何模型
结合实际工程,选取车站西端长59.5 m,宽23.3 m,基坑深20.3 m进行二分之一模型的建立,所以确定该基坑模型尺寸为长120 m,宽75 m,高85 m。围护结构中,地连墙采用3D 实体单元,内支撑、冠梁、腰梁采用1D 梁单元,地连墙中钢筋采用1D 植入式桁架单元。
2.1.3 定义施工阶段
在定义施工阶段时,根据需求不同,采用渗流分析、渗流-边坡耦合分析、固结分析、完全应力-渗流耦合分析等几种分析方式。
⑴初始应力场分析:阶段类型选为应力,施加所有原状土和围护结构,激活自重和边界约束,同时对位移清零;
⑵工况1:(应力)开挖到冠梁安装点以下0.5 m处,安装冠梁和第一道撑;
⑶工况2:(应力)开挖到第一道腰梁安装点以下0.5 m处,安装腰梁和第二道撑;
⑷工况3:(应力)开挖到第二道腰梁安装点以下0.5 m处,安装腰梁和第三道撑;
⑸工况4:(应力)开挖到设计标高,施工完成。
2.2 不同施工工况下两种模型的基坑变形分析
工况1、工况4 基坑位移云图分别如图5、图6 所示,在开挖过程中,模型整体土体位移基本变化一致。根据工况1~工况4 过程中y、z方向位移云图,在施工进行过程中,随着开挖深度的逐渐加深,围护结构外土体的位移逐渐加大,向基坑偏移趋势愈加明显;同时从y方向位移云图可知地连墙水平位移最大绝对值随着开挖深度增加而下移,位于该开挖阶段的底部,围护结构变形量呈现两端小中间大的分布规律,外侧土体的水平位移最大绝对值逐渐远离围护结构。从z方向位移云图可看出随着开挖深度增加,围护结构外围的土体沉降量逐渐增加,且向水平方向和竖直方向的辐射范围逐渐增大。经过位移云图分析,两种模型在开挖过程中,水平和竖向位移变化趋势基本保持一致,土体在自重的影响下对基坑围护结构影响逐渐加大,位移逐渐增加,同时内支撑支护使得上部土体和地连墙的水平位移限制,最大位移随之下移。由此可看出,通过数值模拟验证了等效地连墙的可靠性。
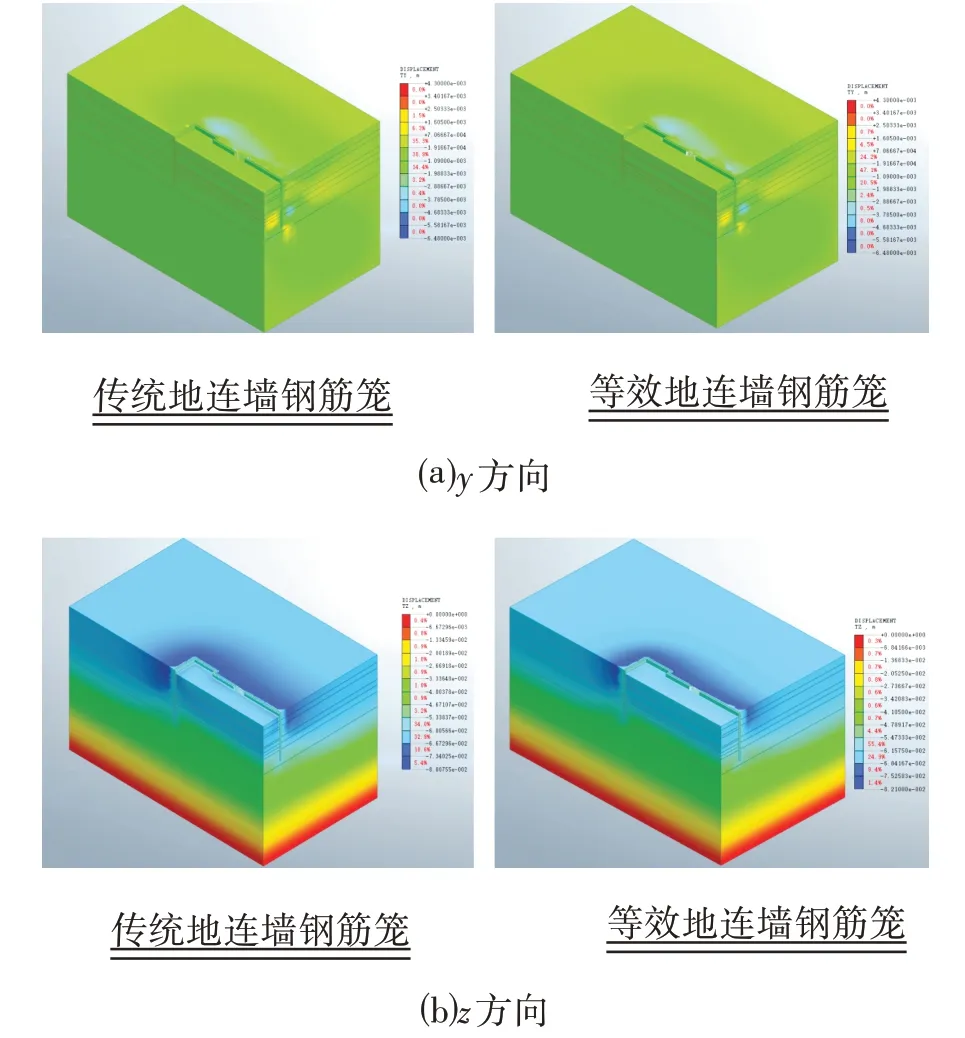
图5 深基坑工况1水平位移云图Fig.5 Nephogram of Horizontal Displacement of Deep Foundation Pit under Working Condition 1
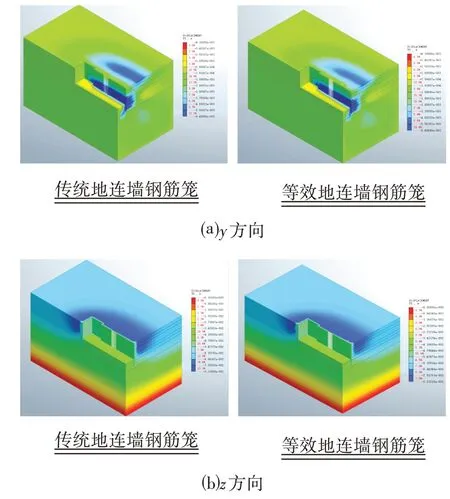
图6 深基坑工况4水平位移云图Fig.6 Nephogram of Horizontal Displacement of Deep Foundation Pit under Working Condition 4
在基坑开挖施工过程中,在土体自重作用下,基坑的围护结构会产生水平位移,随着基坑开挖深度的增大,水平位移逐渐变化。围护结构水平位移云图如图7所示,可知基坑开挖深度逐渐加深,地连墙两侧的土压力差值也逐渐增大,墙体的水平位移也逐渐加大,最大水平位移逐渐加大而且位置不断下移,两模型位移变化趋势保持一致,模拟结果合理。比较两模型相同工况下水平位移云图,可知相同工况、相同位置上,圆形钢筋笼模型地连墙的水平位移小于方形钢筋笼模型。
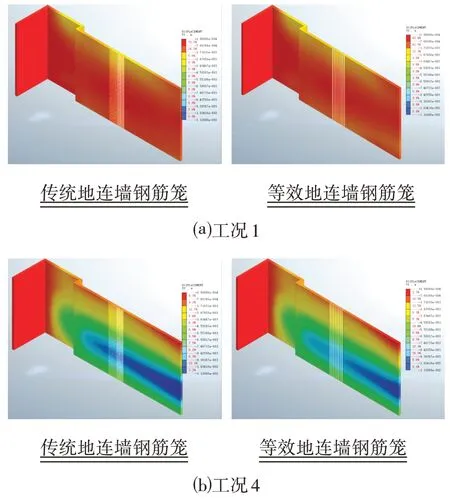
图7 围护结构水平位移云图Fig.7 Cloud Diagram of Horizontal Displacement of Enclosure Structure
工况1、工况4 的钢筋笼轴力云图如图8 所示,进
行对比分析,可以看出模拟开挖过程中,随着开挖深度的增加钢筋受力逐渐增大,且最大值和最小值位置均位于最新开挖阶段的内支撑支护水平线处,这是由于土体自重影响随着基坑开挖逐渐增大,坑底支护的受力也逐渐增大。两模型变化趋势保持一致,因此两模型建立合理,可进行对比分析。从相对应工况下钢筋的受力云图对比中可以看出,在同一工况下,圆形钢筋笼同一位置的轴力最大值小于方形钢筋笼,而且随着开挖深度的增加,两者差距就越明显。同时,方向钢筋笼两侧对称布置钢筋完全相反,而且差值较大,不利于地连墙的安全性考虑;而圆形钢筋笼模型在水平上呈现圆形,只有靠近两侧的钢筋受力差值较大,其余钢筋依次排布靠近中轴线,整体受力在水平面上成阶梯式分布,受力减小,受力较为合理,利于地连墙的安全。
3 结论
本文采用MIDAS GTS 有限元软件进行地铁深基坑等效地连墙受力变形机理研究,分析不同工况下传统地连墙与等效地连墙的受力变形规律;通过基坑变形云图、围护结构变形云图以及钢筋笼轴力对比,验证了等效地连墙的有效性;在相同条件下,等效地连墙的设计相比传统地连墙,能够为基坑提供更好的围护效果,为等效地连墙的工程应用提供理论支撑。
