一类新型热声式换能器阵列的数值仿真

李厚洋，仝真真,2，王金鑫，周震寰

（1. 大连理工大学 工程力学系，辽宁 大连 116024；2. 大连交通大学 机车车辆工程学院，辽宁 大连 116028）

0 引言

由多个激励源构成的声波换能器阵列可以有效控制其声场辐射方向[1-6]，被广泛应用于医学成像[7]、无损评估[8]和定向扬声器制造[9]等领域.该类声波换能器阵列中的单元通常由压电材料制造而成[10]，其激发的声波强度和频响范围主要依赖压电材料的性能[11].然而，现有压电材料的频响带宽较窄[12]，产生的声压通常在10 Pa 以下，并且存在串扰，直接影响声波换能器阵列的指向性精度[13].

近年来的研究发现从超顺排碳纳米管（CNT）阵列中抽取的CNT 薄膜是一类具有良好热声效应的纳米材料[14].通过在其两端施加交变电流可以产生温度振荡，同时引起周围气体介质的膨胀和收缩，进而产生声压级较大的声波.由于该类CNT 薄膜还具有较低的单位面积热容，激发声波具有较宽的带宽.此外，CNT 薄膜还有具有良好的柔性、可拉伸性、高透明性和加工简单等诸多特点.

目前，基于CNT 薄膜的声波换能器已经引起国内外学者的广泛关注.ALIVE A E 等[15]研究了CNT薄膜热声换能器在水下及惰性气体封装结构中的热声响应.LIM C 等[16]提出了悬空CNT 薄膜和CNT 薄膜封装结构的理论模型，将激发声场分为近场和远场两部分解析求解.XU W 等[17]通过点源叠加法获得了CNT 薄膜阵列激发声场的解析解.

上述理论研究以解析分析为主，激发声场求解受到诸多限制，例如仅限于规则形状和分布的薄膜、均匀的气体介质等.为解决该问题，基于COMSOL Multiphysics 软件，对CNT 薄膜热声式换能器阵列激发声场进行数值仿真，为CNT 薄膜热声式换能器阵列的设计和优化提供理论依据.

1 热声换能器数值模型

1.1 几何模型及边界条件

采用COMSOL 中的热黏性声学模块模拟，基于CNT 薄膜的声波换能器的热声响应，其控制方程为

由于求解热黏性声学模型的过程包含了声压、速度和温度3 个变量，严重降低了计算效率.由热黏性声学理论可知，声波的损耗大多数来自靠近声源表面的薄层内，称作黏性边界层和热边界层[18].因此，可以对计算区域进行分区处理，在声源附近区域使用热黏性声学模块，在余下区域使用压力声学模块（等熵绝热传播）.压力声学模块的控制方程为

式中，qd为偶极子源向量，W/m3；keq为波数，m-1，为声速，m/s；Qm为单极子源，W/m3.

两类计算区域的界面连续性条件为

式中，n为交界面的单位法向量.

薄膜表面的边界条件由薄膜表面S的温度变化和声压梯度决定，即

式中，Ts为薄膜表面温度的变化量，K.

选用完全匹配层（PML）作为吸收边界，截断计算区域，该吸收边界在吸收传至边界的声波的同时不发生反射[19].

区域内介质参数从COMSOL 的内置材料库获得，见表1，CNT 薄膜的材料属性来源于文献[14]，整体几何模型及边界见图1.

表1 介质参数Tab.1 partial dielectric parameter

图1 CNT 薄膜阵列的COMSOL 模型Fig.1 COMSOL model for CNT thin film array

1.2 网格划分

三维COMSOL 模型的计算域是均质区域，可以采用自由四面体单元对整体进行网格划分.由于黏性边界层和热边界层的存在以及人为设置的PML，需要对网格进行分区精细处理.

（1）在使用有限元法计算声波传播问题的时候，单元尺寸与波长相关，通常要保证在一个波长尺度内，至少存在6 个单元.因此，将模型的最小单元尺寸设置为波长的1/10.

（2）在靠近CNT 阵列的区域划分边界层网格，边界层厚度为

式中，δthermal为热边界层厚度，m；δviscous为黏性边界层厚度，m.

为了尽量减少反射的数值，将PML 域规则划分网格，如图2 蓝色区域.最后，使用灰色自由四面体网格划分其余计算区域.

图2 PML 网格Fig.2 PML mesh

2 数值算例与讨论

2.1 验证算例

为验证本数值模拟的正确性，以边长为3 cm 的单块正方形CNT 薄膜为研究对象，计算其在空气中的中心轴的声压级（SPL），见图3.由图3 可知，本计算结果在0.05～0.25 m 内与现有理论模型结果一致，表明数值仿真结果具有良好的精度.

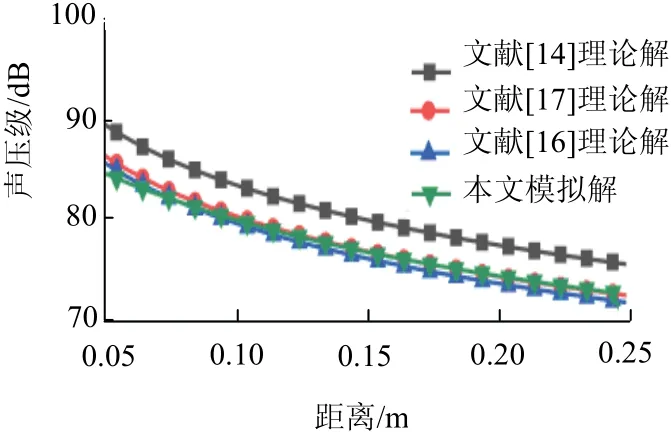
图3 仿真结果与理论解对比Fig.3 comparison between simulation results and theoretical solutions

2.2 阵列几何参数分析

考虑一个3×3 单元CNT 薄膜平面阵列，见图4（a）.阵列中每个单元均为边长1 cm 的正方形CNT薄膜，CNT 薄膜总面积是9 cm2，单元间距为d.

图4 不同排列方式的CNT 薄膜阵列Fig.4 CNT thin film array with different arrangements

为分析单元间距的影响，图5 为d等于1 cm、2 cm、3 cm 时，阵列中心轴SPL 随距离的变化，以及阵列总面积相同的单块CNT薄膜中心轴SPL随距离的变化.图5 中，当CNT 薄膜阵列单元间距由1 cm增加到3 cm 的过程中，中心轴SPL 先增大后减小.将单元间距d的范围扩大到1～5 cm，计算得到中心轴SPL 与单元间距d的变化，见图6.从图6 中可以看出，CNT 薄膜阵列的中心轴SPL 与单元间距高度相关，随距离增加而剧烈波动.由此可知，在热声换能器阵列设计中，应在可行设计范围内合理选取单元间距以提高激发声场强度.

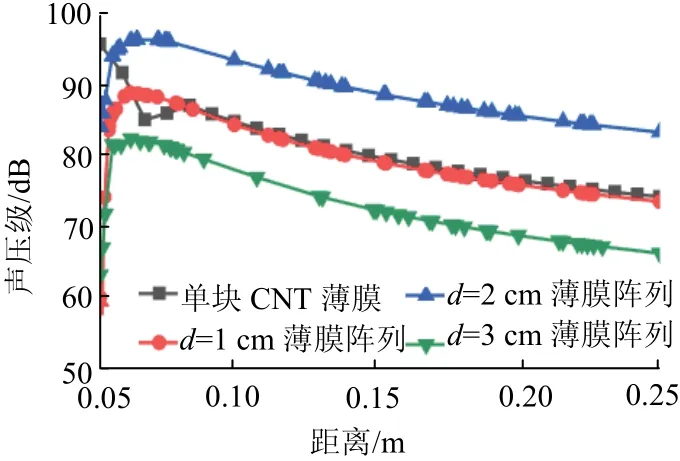
图5 3×3 单元CNT 薄膜阵列中心轴SPL Fig.5 SPL of the 3×3-element CNT thin film array at the center axis

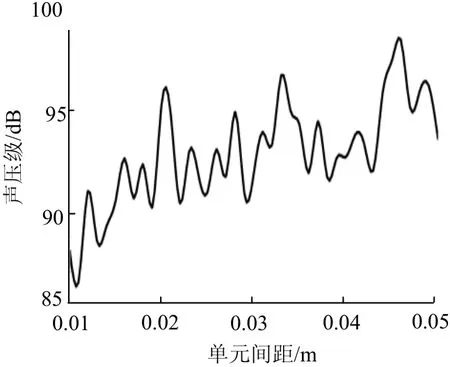
图6 声压级随单元间距变化Fig.6 variation of SPL versustheelement spacing

除了阵列中心轴声压外，声场分布也是热声换能器的重要指标之一.在CNT 阵列上方5 cm 处取一平面，声压分布见图7.图7（a）、图7（b）、图7（c）对应的阵列间距d分别为3 cm、2 cm、1 cm，图7（d）表示单个CNT 薄膜.可以看出，单元间距会对声场分布产生显著影响，图7（b）的焦域（红色部分）面积最大，图7（a）的焦域面积最小.在单元间距由1 cm 增大到3 cm 的过程中，焦域面积出现先增大后减小的趋势，并且图7（a）的焦域形状出现明显变形.

图7 X-Y 平面声压分布（Z =5 cm）Fig.7 X-Y distribution of sound pressure at Z=5 cm

2.3 封装气体参数分析

使用惰性气体对CNT 薄膜进行封装，可以有效保护声源和提高换能器性能[15].为研究不同的封装气体对换能器性能的提升作用，建立了3×3 单元平面阵列的双层介质模型，将热黏性计算区域介质设置为惰性气体（氩气、氦气），压力声学计算区域为空气，单元间距d为2 cm.

图8 封装换能器中心轴声压级Fig.8 SPL of encapsulated transduceratthecenteraxi

从图8 可见，氩气封装的CNT 阵列声压有小幅提升，而氦气封装的CNT 阵列声压降低了约10%.

通过分析表1 的参数发现，声速、导热系数和密度可能是影响声压的重要参数.为进一步研究上述参数对声压的影响，以氩气封装的CNT 薄膜阵列为研究对象，计算点设置为（0,0,0.05），人为修改氩气声速、导热系数和密度.计算点SPL 随声速、导热系数和密度的变化，见图9～图11，设标准空气中的声速为c0，声速由c0增加至10c0，声压下降22%；导热系数由0 增加至1.0 W/(m·K)，声压下降30%；密度由0.2 kg/m3增加至2.0 kg/m3，声压升高18%，并且曲线在1.0 kg/m3后趋于平缓，上述现象表明合理选择封装气体可以大幅提高热声换能器阵列的声场强度.

图9 声压级随声速比变化Fig.9 variation of SPL versus the speedratio of sound

图10 声压级随导热系数变化Fig.10 variation of SPL versus the thermal conductivity

图11 声压级随密度变化Fig.11 variation of SPL versus the density

3 结论

基于COMSOL 软件发展了一类新型热声换能器——CNT 薄膜阵列的仿真方法，并分析了其声场特性，结论如下.

（1）通过与解析解模型对比发现，所提出数值仿真方法具有良好的精确性.

（2）换能器阵列的激发声场强度、指向性与其几何参数高度相关，合理选取单元间距可以有效控制声压大小、聚焦区域面积和形状.

（3）换能器阵列的激发声场强度与封装气体参数高度相关，导热系数小和密度大的气体介质能够显著提高声压.