穿墙雷达墙体与目标回波信号学习分离方法

卞 粱， 晋良念，2， 刘庆华

(1. 桂林电子科技大学信息与通信学院， 广西桂林 541004； 2. 广西无线宽带通信与信号处理重点实验室， 广西桂林 541004)

0 引言

超宽带穿墙雷达三维成像不仅能提供距离向和方位向上的目标位置信息，还能提供俯仰等更多维度的信息，满足了建筑内部的结构特征、人体目标的姿势等信息的需求[1]。由于墙体杂波和噪声干扰，静止目标的弱反射信号很容易被墙体的强反射信号淹没，因此获取的雷达数据往往无法提取静止目标信息[1]。

根据现有研究，墙体回波具有低秩性和目标回波或目标像具有稀疏性的特征，使得墙体回波与目标信号的分离可以构成一种联合低秩与稀疏问题，这样我们将低秩稀疏问题求解就可以提取我们需要的墙体回波和目标信号。文献[2]利用墙体回波为低秩矩阵和目标像为稀疏矩阵的特点，提出了一种低秩联合稀疏成像的方法，并采用可迭代软阈值算法进行分离目标墙壁回波和目标像。文献[3]在此基础上，通过增加全变分(Total Variation，TV)约束提高了目标区域的空间连续性，抑制了背景噪声，将墙壁杂波抑制和目标图像重建的任务描述为一个包含低秩、联合稀疏和TV正则化项的优化问题。文献[4]首先采用快速迭代软阈值算法(Fast Iterative Shrinkage Thresholding Algorithm，FISTA)快速求解低秩稀疏问题分离墙体与目标回波，然后使用增广拉格朗日函数求解全变分约束下凸优化问题，最后使用交替方向乘子(Alternate Direction Multiplier Method，ADMM)方法求解增广拉格朗日函数从而求解稀疏系数。

以上方法虽然能够分离出墙体回波和目标回波，但凸优化算法往往需要预先确定阀值参数。阈值参数影响着奇异值的划分，即影响着墙体与目标回波的划分，所以恰当地选择该参数对墙壁与目标回波的分离具有非常重要的影响。目前的凸优化方法都是基于人工经验选择，具有很强的不确定性。目前，深度神经网络(Deep Neural Networks，DNNs)已经在图像增强、图像识别等领域展现出优势[5-7]。文献[8]中基于低秩-稀疏问题，在医学领域将分离微气泡信号和组织信号的迭代算法展开成神经网络结构。

鉴于此，结合文献[8]的展开策略应用于墙体与目标回波信号的分离。本文在穿墙雷达低秩-稀疏问题的基础上，利用迭代软阈值分离算法求解稀疏解，并将其迭代过程展开映射成多层神经网络结构，即学习迭代软阈值算法(Learning Iterative Shrinkage Thresholding Algorithm，LISTA)网络，通过数据驱动方式学习阈值参数，实现阈值参数的参数自动选取，进而实现墙体与目标回波信号高质量分离。

1 信号模型

如图1所示，使用收发共置的面阵放置在平行于墙面方向对目标区域进行探测。系统发射步进频率信号，扫频范围从f0开始，步进频率为Δf，频率点数为I，每个脉冲的宽度为ΔT，脉冲重复周期为Ts，对应带宽B为(I-1)Δf。

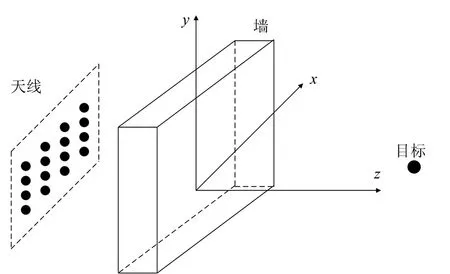
图1 穿墙雷达探测场景图

采用M行N列二维收发共置天线阵列，雷达的发射信号可以表示为

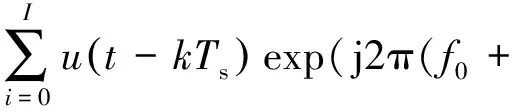
iΔf)t)

(1)

式中，u(t)为矩形脉冲，可以表示为u(t)=rect(t/T)。

对接收到的回波进行混频和离散采样后，回波信号应由耦合波、墙体回波、目标回波和噪声四部分构成。在滤除耦合波后，得到包含后三部分回波的信号矩阵，则雷达回波模型可以表示为

(2)

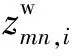
(3)

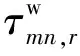
(4)

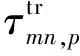
对回波信号zmn,i作快速傅里叶逆变换(IFFT)，可得

ymn,q=IFFT(zmn,i)

(5)

即

(6)

式中，

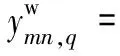
(7)

(8)

式中，Q为采样总数，q为第q个采样点。

将这MN个通道测得的所有数据构成矩阵，可得

Y=Yw+YTR+V

(9)

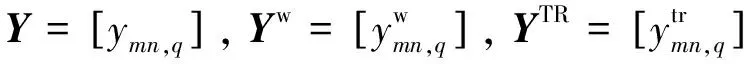
2 算法描述

目标回波矩阵YTR的提取是目标成像的关键，必须消除墙体回波Yw和噪声V的干扰。目标回波矩阵是一个稀疏矩阵，墙体回波矩阵则是一个低秩矩阵。矩阵秩的求解是一个非凸问题，近似解为其核范数，可用奇异值阈值算子进行求解，而稀疏成分通常用l1范数最小化模型求解，即

(10)

其中，‖·‖*为核范数，它是矩阵Yw的奇异值之和，‖·‖1为1范数，它是矩阵YTR的矩阵值之和，‖·‖F为弗洛贝尼乌斯范数，它是矩阵的内积，λ为反映低秩项和稀疏项之间权衡的正则化参数，ε为噪声限制。

由文献[9]可知，通过凸分析，式(10)可以转化为无约束的拉格朗日正则化形式：

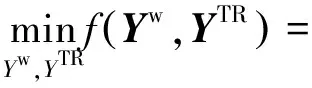
‖Yw‖*+λ2‖YTR‖1

(11)

考虑最小化复合目标函数一般情况，式(11)可以转化为

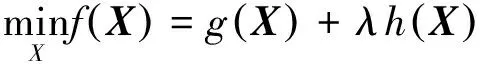
(12)

其中，g(X)是凸函数，光滑的，可微的，代表式(11)中的二次项，h(X)是凸函数，但不一定光滑，代表式(11)中的核范数和1范数。

解决式(12)的方法是利用迭代过程求解目标函数，在第t次迭代过程中生成估计解Xt， 则下一个最小估计解可以表示为

(13)

式中，Ut=Xt-α∇g(Xt)，∇g(Xt)为当前估计Xi下g(X)的梯度，α为调整步长。式(13)将式(11)中的组合最小化问题分解成两个子问题求解，式(11)可以表示为

λ1‖Yw‖*+λ2‖YTR‖1

(14)

由式(13)可得

(15)

式中，Y0为原始回波。将核范数与1范数分离，将式(11)分解成两个子问题使目标函数最小化，可得

(16)

(17)

式(16)可以通过奇异值阈值算子方法求解，为

(18)

式中，ηsvd(·)为奇异值阈值算子，定义为ηsvd(Y)=GΓ(Λ)VH，这里，Y=GΛVH为Y的奇异值分解，Γ(·)为软阈值算子，定义为

Γ(xt)=(|xt|-λ)sign(xt)

(19)

将式(15)代入式(18)中，得

(20)

式(17)可以通过迭代软阈值方法求解，为

(21)

同样地，将式(15)代入式(21)中，得

(22)

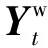
表1 墙体与目标回波分离方法流程

感兴趣目标反射强度的不同以及墙体介质的不同，人工无法凭借经验选择合适的阈值参数λ1,λ2，导致墙体回波所代表的奇异值难以准确划分，进而难以准确获取目标回波。根据文献[8]的模型驱动学习方法，将墙体与目标回波的分离过程展开成多层神经网络LISTA分离网络，其中第t次迭代可以看作网络中第t层，然后通过数据驱动进行学习阈值参数，单层LISTA分离网络如图2所示，则第t层网络表达式可以表示为

(23)

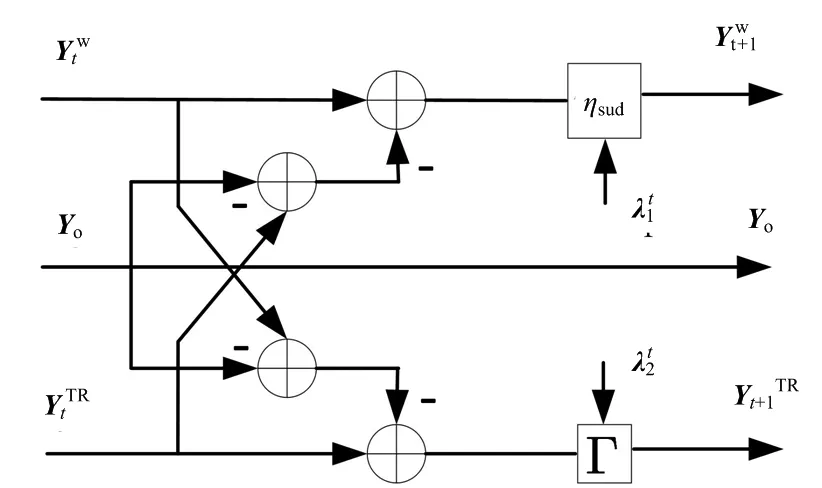
图2 单层LISTA分离网络

(24)

式中，N表示训练样本数，n为第n个样本，f(Yw,Θ)为网络输出预测墙体回波的重构结果，f(YTR,Θ)为网络输出预测目标回波的重构结果，L(Θ)表示归一化的均方误差。采用Adam方法进行求解，Adam方法利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率，其更新参数过程为

(25)

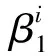
3 仿真与实验结果分析3.1 仿真数据处理结果分析

仿真数据由电磁仿真软件GprMax软件产生，仿真场景如图3所示，该场景用ParaView软件生成。仿真空间为2 m(长)×1 m(宽)×1 m(高)的区域；墙体为均匀介质，长度、厚度、高度分别为0.9 m，0.2 m，0.9 m，相对介电常数为6，网格单元为0.01 m；天线平面阵列由17行18列收发共置阵元组成，在方位向上0.1 m到0.9 m之间、在高度向上0.05 m到0.9 m之间，阵元间距0.05 m；该阵列平行于墙体进行放置，距离墙体0.1 m；以不同频率的正弦波信号模拟步进频信号，其初始频率为1 GHz，终止频率为3 GHz，步进频率为20 MHz，单频时间窗为50 ns，采样时间窗为6 μs。下面，设验证场景为放置在空间坐标为[0.4,0.6]×[1.0,1.2]×[0.4,0.6]的体目标，信噪比为0 dB。

图3 仿真场景示意图

选取面阵中第10行第10列雷达天线接收回波观察，如图4所示，图中已标出墙体和目标回波出现位置，从图中可以看出，墙体回波幅度远远大于目标回波，几乎掩盖目标回波。真实墙体和目标回波如图5所示，其中目标回波用背景相消法[11]生成。

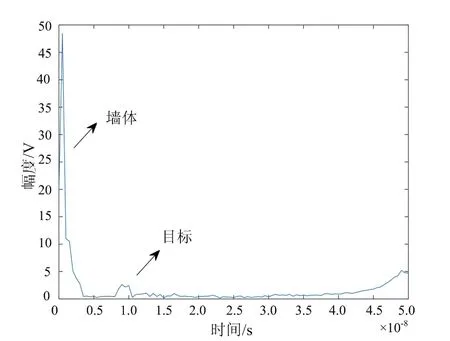
图4 雷达接收回波

(a) 真实墙体回波

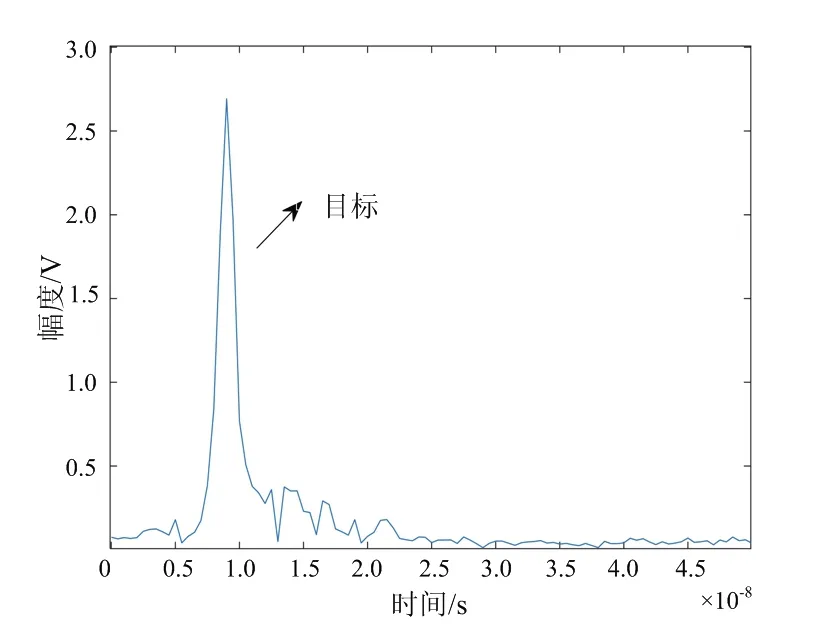
(b) 真实目标回波图5 真实墙体回波与目标回波

首先，观察不同阈值参数下分离算法分离效果，如图6所示。其中，图6(a)为λ1=30,λ2=0.05时分离的目标回波，从图中可以看出墙体回波在目标回波中影响以大幅缩减，可以准确观测出目标回波的位置；图6(b)为λ1=20,λ2= 0.05时目标回波，与图6(a)作对比，可以看出λ1=20时对墙体影响在目标回波中进一步缩减，λ1影响着墙体回波与目标回波之间的划分；图6(c)为λ1=20,λ2=0.1时目标回波，与图6(b)作对比，可以看出λ2=0.1时进一步消除了目标回波的噪声，λ2影响着目标回波与噪声之间的划分。

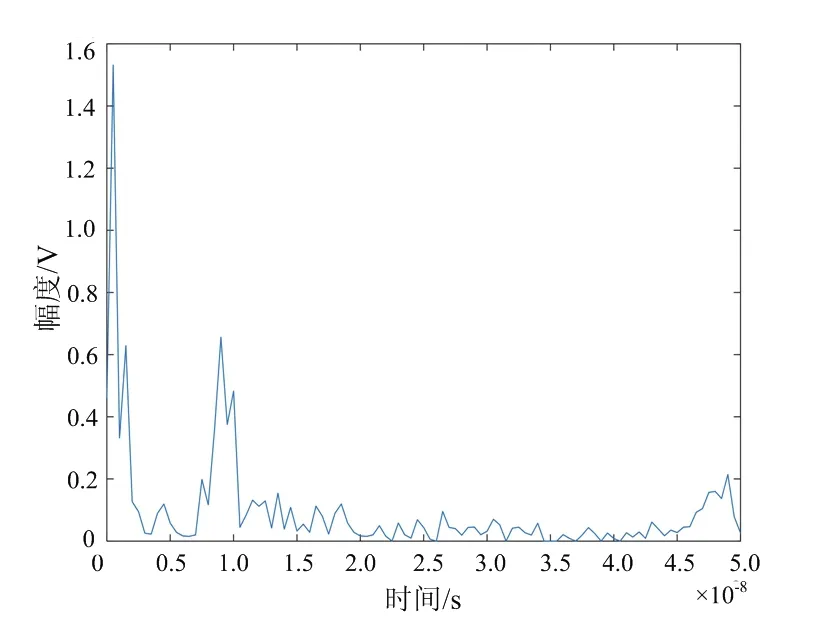
(a) λ1=30,λ2=0.05时目标回波

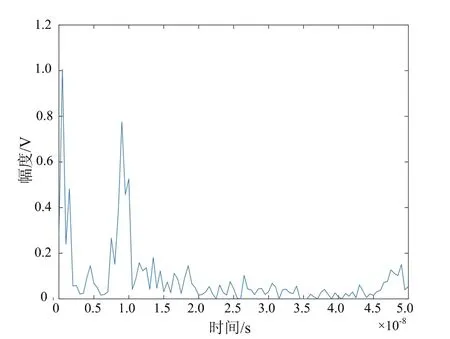
(b) λ1=20,λ2=0.05时目标回波

(c) λ1=20,λ2=0.1时目标回波图6 不同阈值参数下分离算法分离效果

接下来构建数据集训练LISTA网络，我们将目标均设置在空间内的任意位置，目标数目为1到2个，另外根据目标信号增加信噪比为0 dB到5 dB的噪声以增加训练集数据，一共生成100组样本。实验平台在配置为Intel i7，24GB RAM，GTX1050Ti的电脑上完成，所提LISTA网络利用Python torch编写实现。

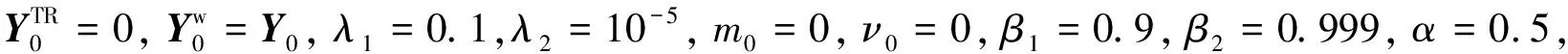
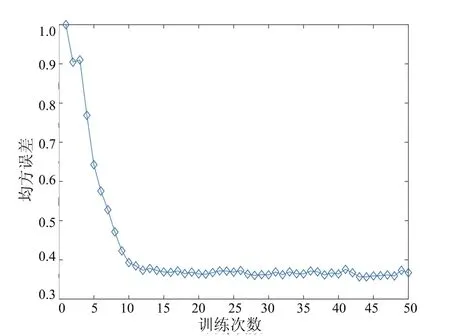
图7 归一化均方误差

(a) 预测墙体回波

(b) 预测目标回波图8 预测墙体回波与目标回波

分离网络下验证场景回波结果如图8所示，图8(a)为预测墙体回波，图8(b)为预测目标回波，可以看出在没有手工调整阈值参数的情况下，分离网络得到的墙体与目标回波分离，准确得到了目标回波。图9为使用后向投影(Backward Projection，BP)[12]算法成像结果，左上图为沿距离向z=1.1 m处方位-高度切片图，右上图为沿高度向y=0.5 m处方位-距离切片图，左下图为沿方位向x=0.5 m处距离-高度切片图，右下图为三维立体图，从成像结果上所得目标回波可以准确对目标定位成像。

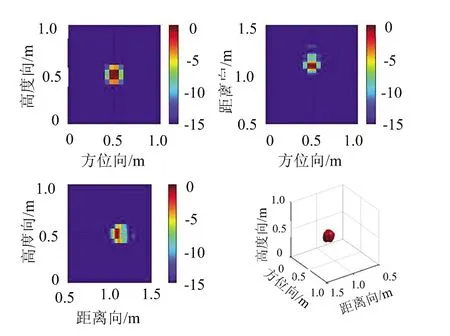
图9 BP算法成像结果

3.2 实测数据处理结果分析

实测数据采用维拉诺瓦(Villanova)大学高级通信中心(CAC)与空军研究实验室(AFRL)合作收集得到的穿墙雷达成像实验数据[13]，探测场景如图10所示。选取65×57平面阵列所得到的数据进行三维穿墙成像，发射信号是载波频率为2 GHz，带宽为1 GHz的步进频率波形，步进间隔为5 MHz。使用生活场景(Populated Scene)回波数据生成训练样本，加入信噪比为0 dB到5 dB范围内噪声，一共生成100组样本，设置γλ1=0.002，γλ2=10-5，其余参数与仿真实验设置相同，训练时，每次训练数据为10组，共计训练50次，经过训练后得到的λ1=[0.153 0, 0.051 3, 0.164 6, 0.145 8]，λ2=[-0.000 2, 0.000 3, 0.000 1,-0.002 3]。

(a) 探测场景图

(b) 雷达穿墙场景图图10 实验场景

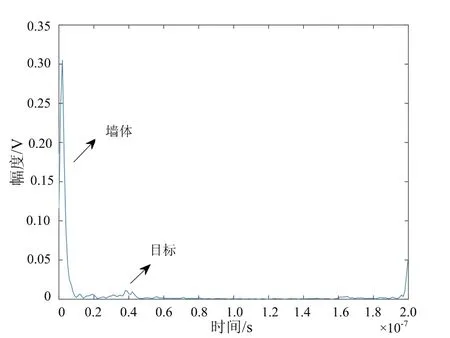
图11 雷达接收回波

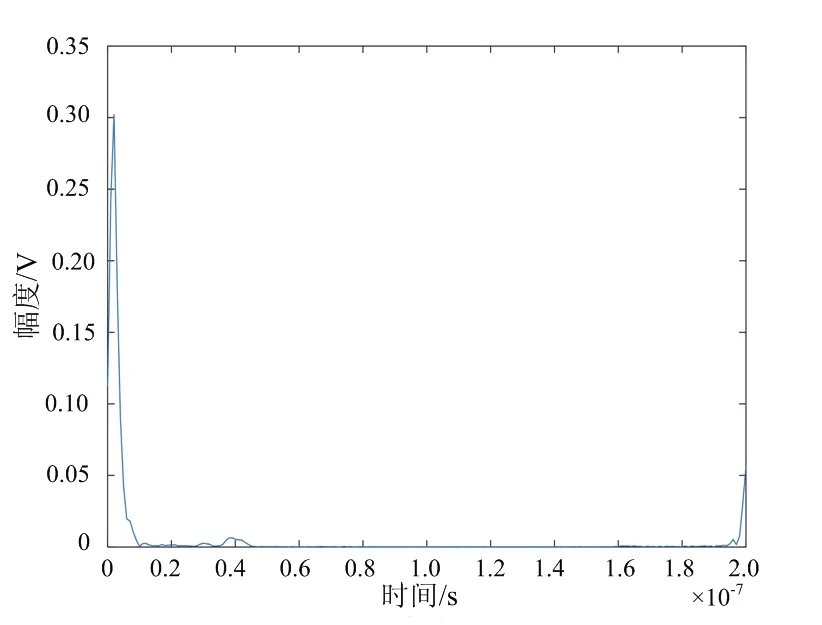
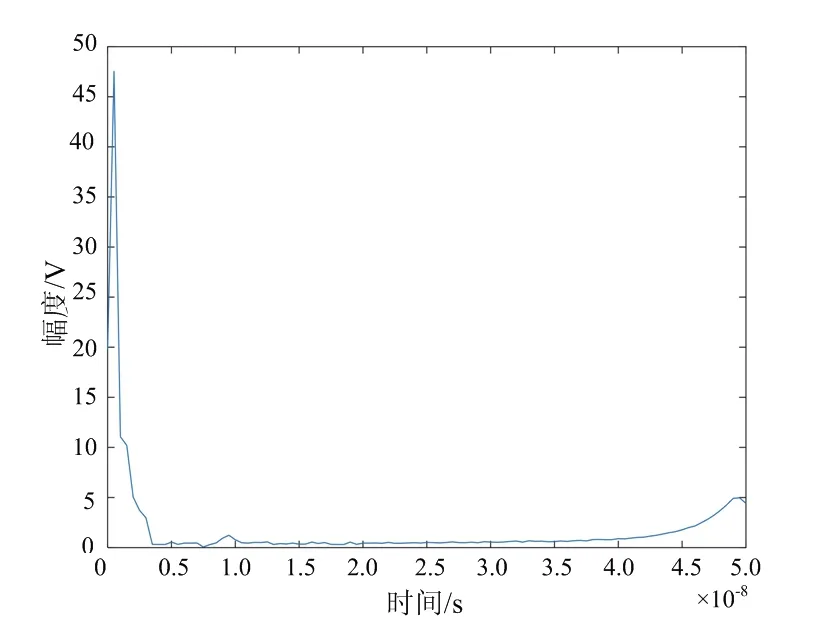
(a) 预测墙体回波

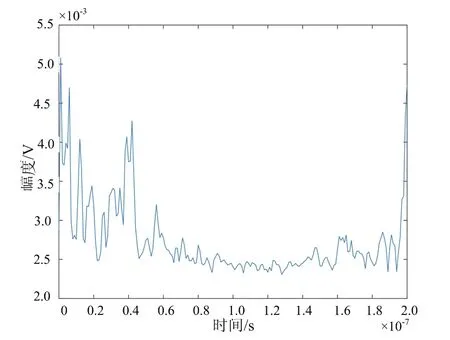
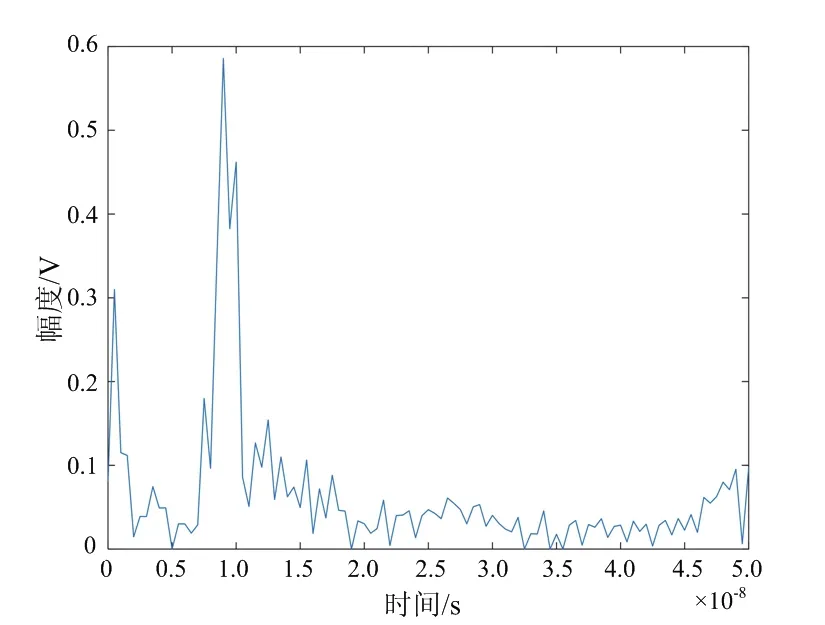
(b) 预测目标回波图12 LISTA网络分离结果

使用校准场景(Calibrated Scene)进行实验验证，图11为该场景下第36行第28列原始回波，图12为LISTA分离网络后墙体回波与目标回波，可以看出，原始回波信号中墙体回波远大于目标回波，淹没了回波信号，分离网络得到的墙体与目标回波去除了杂波，准确得到了目标回波。图13为分离后目标回波BP算法成像结果，图13(a)为三维立体图，图13(b)为高度向1.2 m处切片图，从结果上看出，分离后的目标回波可以准确对目标定位成像，与仿真结果基本一致。

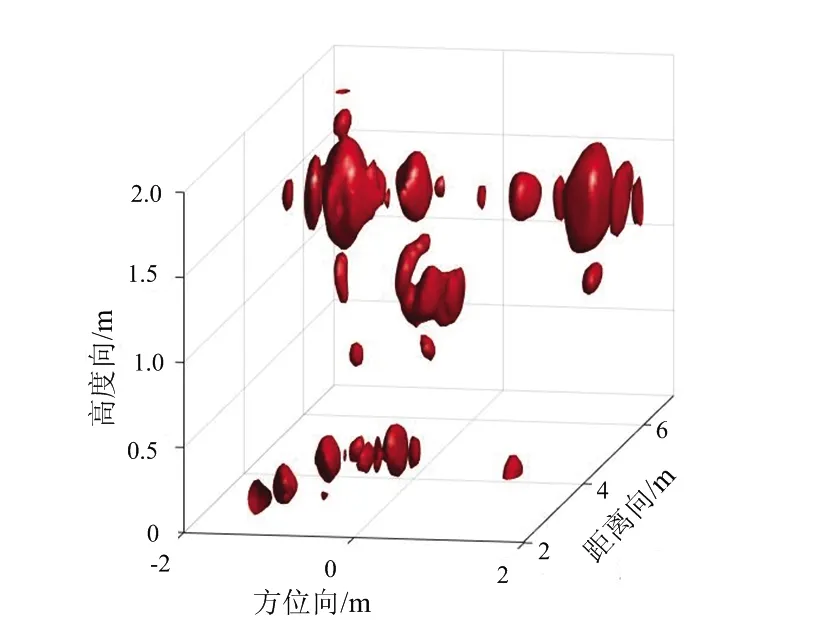
(a) 三维成像立体图

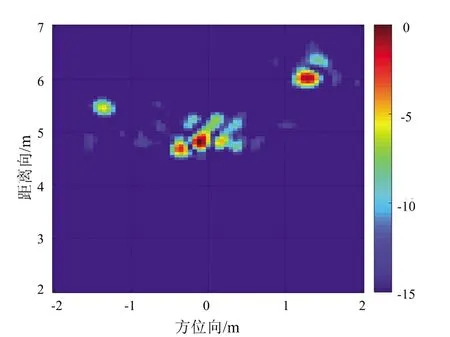
(b) 方位-距离向切片图13 BP算法成像结果

4 结束语

本文提出了一种墙体与目标回波信号学习分离方法，通过将迭代软阈值算法的迭代过程映射成神经网络结构，训练其中的阈值参数，实现阈值参数的自动调整，避免人工选取对分离效果的影响。还需注意的是：在实际情况中，面对墙体介质的多变性和非均匀性，需要进一步对网络结构和训练样本作一定的更改，增加网络训练参数，以增加网络的非线性拟合能力。下一步拟使用分离后墙体回波与目标回波实现对墙体参数的估计和自聚焦成像。