基于灰色动态多属性群决策方法的农业旱灾应急管理

罗 党，郝慧慧

（华北水利水电大学管理与经济学院，郑州450046）

0 引言

旱灾是造成我国经济农业损失最为严重的自然灾害之一[1,2]。据统计资料显示，2000年全国农作物受灾面积高达4 054 万hm2，绝收面积800 万hm2。旱灾造成粮食损失近600亿t，经济损失近500 亿元[3]。河南省是我国农业大省，农业是其受旱灾影响最为严重的行业。2014年河南省遭受了63年来的特大干旱，全省50%的河流断流，局部地区秋粮严重受损甚至绝收。《中华人民共和国国民经济和社会发展第十四个五年规划纲要》建议指出，我国自然灾害防御水平明显提高。但随着全球气候变暖，极端天气频发，区域社会、经济、农业快速发展，需水量剧增，旱灾风险问题越来越突出[4-7]。为减轻农业旱灾风险，采取旱灾应急管理措施，提高适应和应对能力，加快补齐防灾减灾领域的短板，推进防洪减灾等强基础、增功能、利长远的重大项目建设，成为当前研究的方向。在实际的农业旱灾应急管理措施决策中，由于决策信息的灰性、决策者知识和经验的局限性、决策方案的动态多属性等方面的原因，导致决策者难以合理的对方案进行决策优选。因此，在农业旱灾应急管理决策中充分考虑决策者心理因素的影响，做出科学合理的决策是亟待解决的问题。

梳理现有研究成果发现，针对不确定信息处理，学者多采用语言集[8]、模糊数学[9]、区间数[10]和二元联系数[11]的方法。在实际的研究中发现运用模糊数学和语言集在计算过程中出现误差过大，甚至造成评价结果失真。因此，为克服数据的不确定性，针对一些知道其取值范围和分布信息的不确定性问题，本文以三参数区间灰数刻画数据特征。关于农业旱灾应急管理措施决策，何斌等[12]基于1960-2002年湖南省降雨资料，利用GIS 技术对湖南省农业干旱度的空间格局进行了分析。刘兰芳等[13]采用层次分析法构建了旱灾应急管理能力评价指标体系，进一步提高了旱灾风险管理水平。张乐等[14]对极端干旱应急管理模式构建及应急水资源配置等问题进行了理论探讨，从水资源管理的角度构建了考虑预支付策略下的极端旱灾应急水资源合作储备模型。罗党等[15]基于土壤含水量预测问题中的特征和变化规律，构建了BSGM（0,N）模型预测河南土壤含水量。马显莹等[16]围绕旱灾应急管理的特性，通过调查研究及专家咨询等多种手段，构建旱灾应急响应的管理及技术体系。Estrela 等[17]分析了过去30年西班牙的历史干旱和主要干旱事件以及所采取的行动，强调了公众参与干旱事件决策过程的重要性。Wan等[18]同时考虑了供体和受体水库的入水量，用水量和缺水情况，使用模糊数学和混合Copula 函数建立了水库优化供水调度预警决策系统。在上述研究中，假设决策者是完全理性的。而在实际决策中，决策者的风险偏好常常会影响最终的决策结果。除此之外，大多数文献研究的是单一时间点的静态决策问题。但在实际问题中决策者掌握的决策信息随时间不断发生变化，如投融资金[19]，股票交易[20]，农业旱灾应急管理等很多领域需要考虑多时点的动态决策问题。在这一背景下，动态多属性群决策方法应运而生。

动态多属性群决策问题涉及多个决策者、多个阶段和多个备选方案的多个属性。近年来，广泛应用于经济、管理和社会等诸多领域。因此，本文以河南省农业旱灾应急管理措施为例，针对决策矩阵中的值为三参数区间灰数的动态多属性群决策问题，提出了基于4维矩阵和后悔理论的灰色多属性群决策方法。首先，利用4维矩阵表示各阶段属性值，求解理想效用矩阵。然后，将后悔理论引入理想决策矩阵中，计算正负靶心矩阵与正负理想矩阵的距离，得到综合欣喜后悔值。最后，依据各方案的综合欣喜后悔值选出农业旱灾应急管理的最优方案，实现农业旱灾应急管理的综合评价。

1 预备知识

1.1 三参数区间灰数

动态多属性群决策问题涉及4个维度：时间、决策者、属性和备选方案，本文以4维空间中相应坐标轴上的点表示备选方案的属性值。

1.2 后悔理论

后悔理论最早由Bell[22]、Looms 和Sudgen[23]在1982年提出，是指在决策过程中决策者会根据其选择方案获得的结果与其他方案可能的结果进行对比，因而产生欣喜和后悔两种心理，并试图避免选择使其后悔的方案，即决策者是后悔规避的[24]。这是一种在放弃独立性公理的前提下，将进行决策的各方案与其心中的理想方案进行对比得到欣喜后悔值。若以正理想方案的决策指标值作为参考点，其他方案与正理想指标值相比劣于正理想指标时，决策者是后悔心理；若以负理想方案的指标值为参考点，其他方案与负理想指标值相比优于负理想指标时，决策者是欣喜心理。定义备选方案si相对于负理想方案的欣喜函数和相对于正理想方案的后悔函数表达式分别如下[23]：

式中：δ为决策者后悔规避系数，δ>0。

决策者对各方案评价值的综合欣喜后悔函数表达式如下：

2 基于4 维矩阵和后悔理论的动态多属性决策方法

2.1 问题描述

设某应急方案决策中，方案集为S={s1,s2,…,si,…,sm}，属性集为U={u1,u2,…,uj,…,un}，决策者集为V={v1,v2,…,vh,…,vp}，阶段集为τ={τ1,τ2,…,τt,…,τT}，备选方案的属性值为Aij。

由于各指标具有不同的量纲，为便于计算比较，需要对原始数据进行规范化处理，本文采用灰色极差变换消除指标量纲。

对于效益型指标：

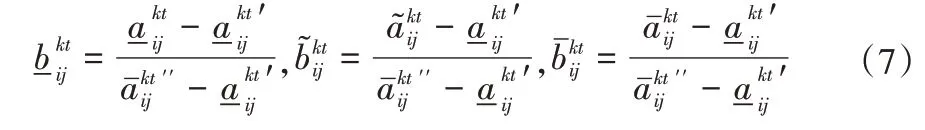
对于成本型指标：

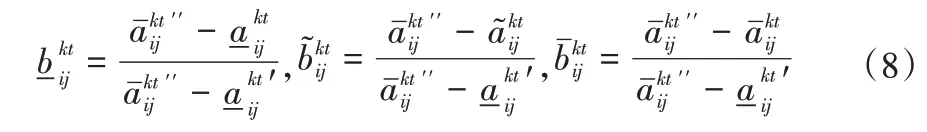
2.2 4 维矩阵的正负靶心矩阵

定义4 属性uj在4维空间矩阵中的正理想矩阵为：

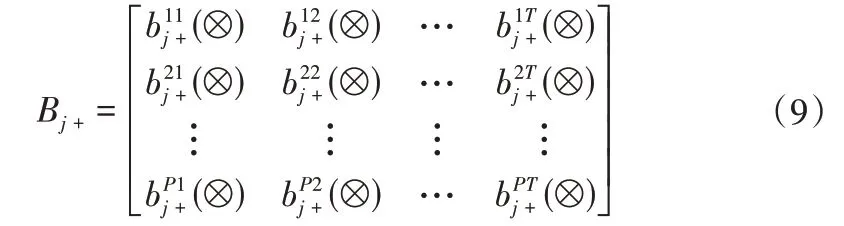
定义5 属性uj在4维空间矩阵中的负理想矩阵为：

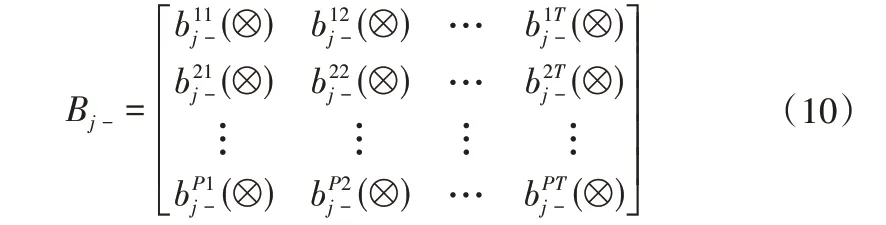
定义6 备选方案si在属性uj下与正理想矩阵的距离为：

式中：λk，τt分别为矩阵坐标中行向量和列向量的权重。

定义7 备选方案si在属性uj下与负理想矩阵的距离为：

则备选方案si与负理想矩阵的距离为：

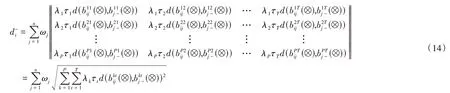
2.3 确定权重

2.3.1 决策者权重的确定

针对决策者权重未知的问题，考虑决策者对最佳方案的偏好越大，决策权重越小的原理进行权重分配。决策者对正理想方案的评价越高，对负理想方案的评价越差，因此本文决策者的权重由最佳正理想方案和最佳负理想方案的距离来衡量，计算如下：

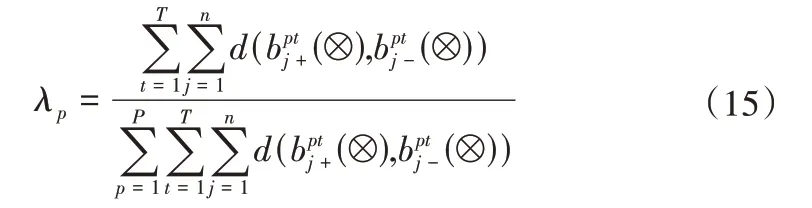
2.3.2 阶段权重的确定

阶段权重体现了决策者对不同阶段的偏好程度，针对不同的实际问题，各阶段权重不能一概而论。通过考虑时间度和问题特征，构建如下优化模型确定阶段权重。设阶段权重向量的时间度为则在给定时间度下阶段权重为：

2.3.3 属性权重的确定

由于各个方案是公平竞争，所以综合欣喜-后悔值越大越好。因此，建立如下优化模型求解属性权重：

式中：λ<ωj确保各属性值均参与决策，λ>0 为临界值，其数值建议设为避免各决策属性值出现鲁棒性，其数值建议设为：

2.4 灰色动态多属性群决策步骤

步骤1 根据已建立的决策指标体系构建评价值为三参数区间灰数的4维矩阵Aij，并根据公式（7）和（8）对矩阵数值进行标准化处理得到矩阵Bij。

步骤2 根据公式（9）和（10）确定各方案的正负理想矩阵Bj+和Bj-。

步骤3 根据公式（15）确定决策者权重λp。

步骤4 根据公式（16）和（17）确定阶段权重τt和属性权重ωj。

步骤5 根据公式（12）和（14）求解各方案与正负理想矩阵的距离和。

步骤6 依据公式（4）和（5）得到欣喜后悔函数，求得各方案的综合欣喜后悔值Zi；最后将其进行大小排序，进而确定最优方案。

3 应用实例及对比分析

3.1 应用实例

自古以来旱灾就是对中国影响较大的自然灾害之一，严重制约了中国的可持续发展[25]。《中华人民共和国国民经济和社会发展第十四个五年规划纲要》建议指出，为保障人民生命安全，应提升洪涝干旱、地震等自然灾害防御工程标准，完善国家应急管理体系，加强应急物资保障体系建设，提高防灾、减灾、抗灾、救灾能力。河南地处黄淮海平原中心，是我国重要的农业生产基地，但因受季风型气候的影响，旱灾频发，干旱问题研究亟需加强。因此本文以河南省农业旱灾应急管理措施为例，通过考虑决策者的偏好程度和心理行为，构建科学决策方法，对备选方案进行综合评价和优劣排序。立足于农业旱灾应急管理系统的基本规律，考虑决策者风险偏好差异性、心理行为复杂性和决策信息多元灰性等不确定性特征构建动态群决策模型。

河南省为应对农业旱灾，采用应急管理进行风险调控以确保粮食产量稳定。通过对农田水利基础设施建设和科学灌溉进行分析，制订了3套农业旱灾应急管理措施，记备选方案集为S={s1,s2,s3}，其中：s1为整合资金，推进小型水利设施新建和维修；s2为加大财政投入，推进黄河引流；s3为落实财政资金，推进节水灌溉工程建设。为提高决策的科学化和民主化，决定采用群决策方法进行方案优选。经过分析讨论组织了3 位相关领域的专家，主要从以下4 个方面对备选方案进行综合评价，记属性集为U={u1,u2,u3,u4}，其中：u1为在特定风险下备选方案能够缓解旱灾的程度；u2为备选方案投入和预期产出的匹配程度；u3为备选方案实施的难易程度；u4为备选方案应对旱灾的必要性程度。为提高决策精度，决策主要分为3 个阶段，对应于粮食生长的3 个过程（以小麦为例，对应于小麦生长的育苗期、生长期和抽穗期），得到3 个方案的三参数区间灰数形式的初始评价矩阵如表1所示。

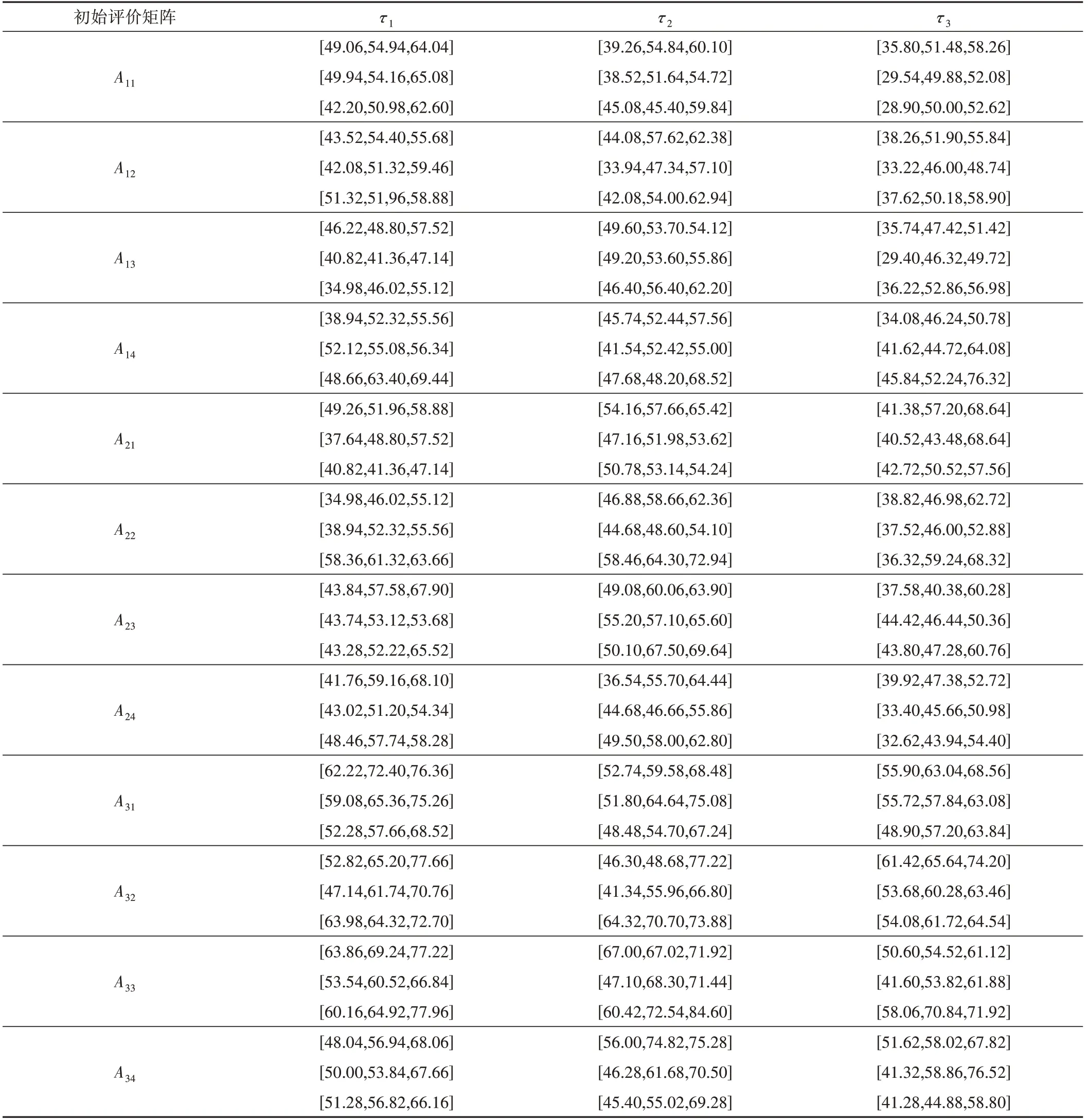
表1 初始评价矩阵Tab.1 Initial evaluation matrix

步骤1 根据公式（7）和（8）对初始评价矩阵数值进行标准化处理，得到表2。

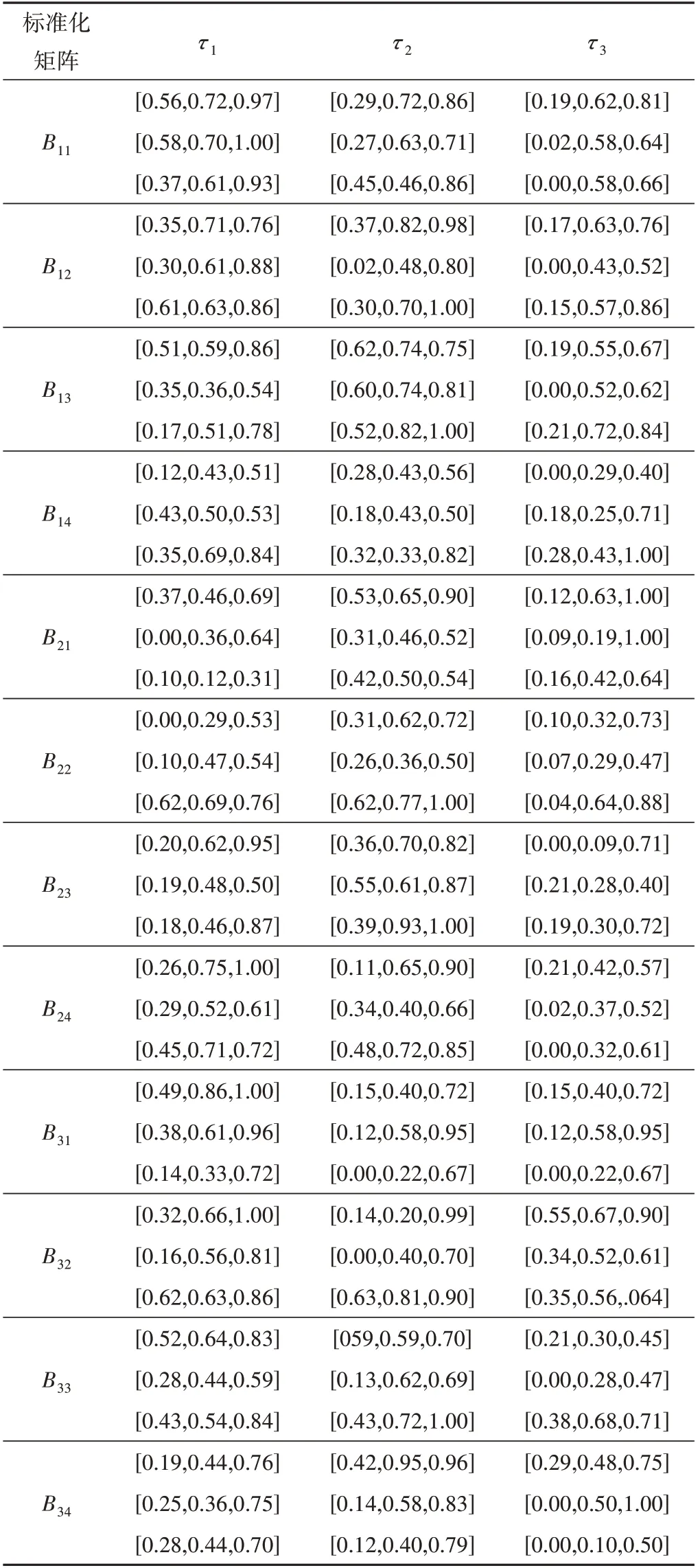
表2 评价矩阵标准化Tab.2 Evaluation matrix standardization

步骤2 根据公式（9）和（10）确定3个方案的正负理想矩阵B1+,B1-；B2+,B2-和B3+,B3-。

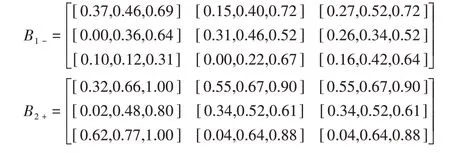
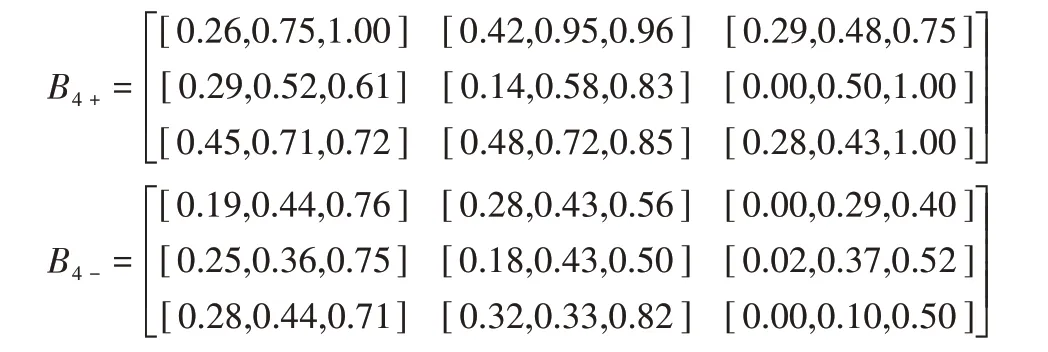
步骤3 采用公式（15）确定决策者权重λp，此时θ= 0.5，表示决策者偏好一致。

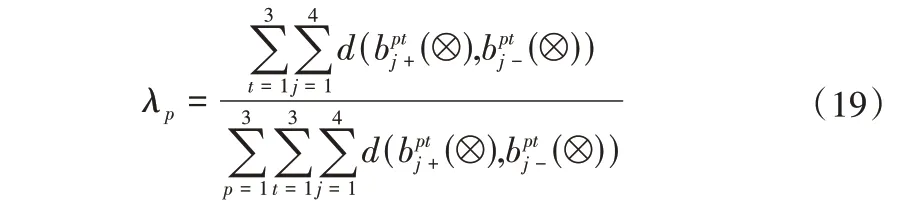
得决策者权重为：λ1= 0.38，λ2= 0.28，λ3= 0.34。

步骤4 根据公式（16）和（17）确定阶段权重τt和属性权重ωj。

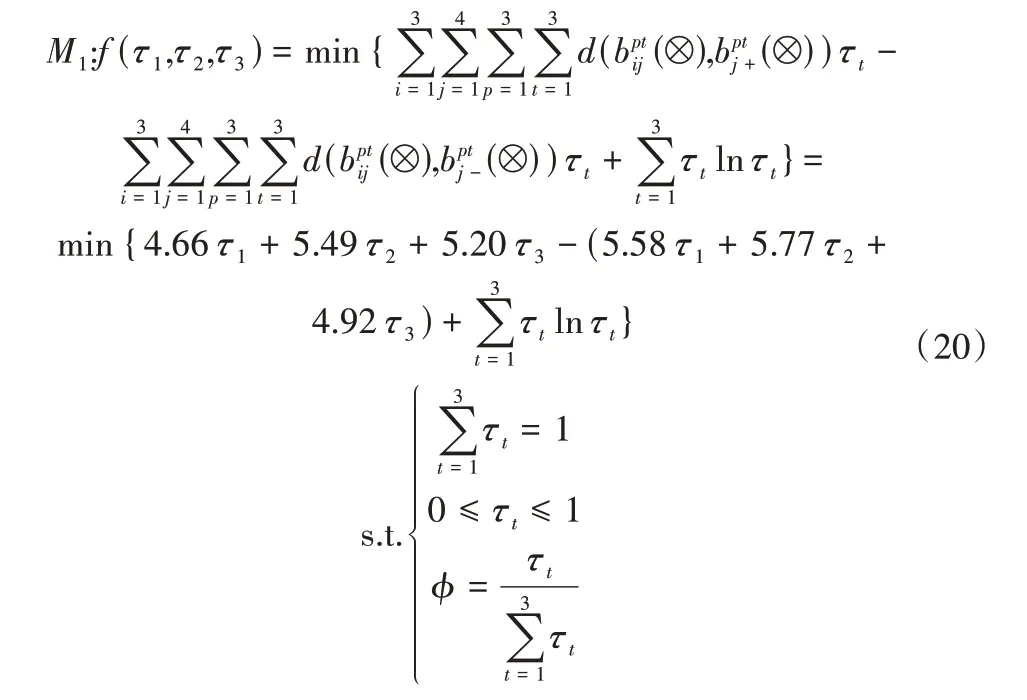
得阶段权重为：τ1= 0.55，τ2= 0.29，τ3= 0.16。

得属性权重为：ω1= 0.275，ω2= 0.300，ω3= 0.300，ω4= 0.125。

步骤5 根据公式（9）和（11）求解各方案与正负理想矩阵的距离为：。

步骤6 依据公式（4）和（5）得到欣喜后悔函数，求得各方案的综合欣喜后悔值Zi，并将其进行大小排序，进而确定最优方案，如表3所示。

表3 各备选方案综合欣喜后悔值Tab.3 Comprehensive joy and regret value of each alternative

根据综合欣喜后悔值越大越优的原则，可以得到3个方案的优劣排序为s1≻s3≻s2，最优方案为s1整合资金，推进小型水利设施新建和维修，最劣方案为s2加大财政投入，推进黄河引流。在当前状况下，应重点整合资金，推进小型水利设施新建和维修。此外，引调黄河水和节水工程建设规模庞大，物资需求巨大，建设周期长，不利于短期应急措施实施。但从长远规划角度出发，应积极争取各方有利资源，进行工程设施建设，保证粮食能够长效稳产增收，降低干旱灾害对农业产生的影响。

3.2 对比分析

为了验证本文模型的有效性，运用文献[26]提出的基于前景理论的三参数区间灰数型群体灰靶决策方法进行对比分析。根据文献[26]中基于前景理论的群决策方法计算各决策方案的前景值和决策者权重，得到各方案的综合前景值为：s1= 0.20，s2= 0.38，s3= 0.73。由综合前景值可知，文献[26]的方法最优方案为s3落实财政资金，推进节水灌溉工程建设。两种方法排序不同的原因是基于前景理论的三参数区间灰数型群体灰靶决策方法考虑的是静态决策，没有考虑阶段属性，而旱灾应急管理决策是动态多属性群决策。同时采用前景理论群决策方法决策过程虽然考虑了决策者的心理行为，但计算过程中涉及的参数较多，对结果影响较大。本文采用基于4维矩阵和后悔理论的动态群决策方法计算过程涉及的参数较少，且决策者不需要给定参考点和权重，评价过程更具有实际意义。

4 结论

针对农业旱灾应急管理措施决策中决策信息的灰性、决策者知识和经验的局限性、决策方案的动态多属性问题，本文考虑属性值为三参数区间灰数形式，引入4维矩阵进行决策属性表述；并考虑决策者受心理因素的影响，引入后悔理论确定决策者的欣喜后悔函数值；构建了基于4维矩阵和后悔理论的三参数区间灰数动态多属性群决策模型，最后依据综合欣喜后悔值进行方案优劣排序。将该模型应用于河南省农业旱灾应急管理措施决策中。结果表明，基于4维矩阵和后悔理论的三参数区间灰数动态多属性群决策模型在进行农业旱灾应急管理决策时准确度较高，通过对比分析进一步验证了本文模型在分析具有不确定性特点的多属性、多阶段群决策问题的有效性。目前，多属性群决策问题在旱灾应急管理方面的应用较少。未来研究可更多考虑既有区间数又有实数的多源数据决策模型，甚至更加复杂的四参数区间灰数动态多属性群决策模型以用于解决融资、管理、防灾减灾等实际问题。