基于元学习和PINN 的变工况刀具磨损精确预测方法

万 鹏，李迎光，华家玘，刘长青

（南京航空航天大学机电学院，南京 210016）

航空航天制造是一个国家科技水平的重要标志，因其高精度和高性能要求而备受行业关注。为保证航空航天产品综合性能及其在极端环境下能够正常工作，钛合金、高温合金等难加工材料广泛应用于航空航天零部件的制造。在零件的数控加工过程中，由于难加工材料强度大、硬度高和热传导系数低，切削刀具刀尖应力大，导致切削刃局部温度较高，刀具更容易发生失效［1-2］。研究表明，在实际加工中，更换刀具的停机时间占机床总停机时间的20%以上［3］，刀具和刀具更换的成本占总加工成本的3%～12%［4］，传统依靠人工经验确定更换刀具的时间节点导致刀具的使用寿命被严重浪费。准确可靠的刀具状态监测系统可通过减少机床停机时间和最大程度利用刀具使用寿命的方式降低10%～40%的生产成本［5］。因此，刀具磨损预测对保证零件加工质量和效率、降低加工成本具有重要作用。

同时，为了满足航空航天产品优良的气动外形和轻质的要求，航空航天零件结构往往较为复杂，外形多由复杂曲面组成，并存在较多槽腔结构。这些因素使得此类零件加工工艺复杂，加工时切削参数、刀具材料和刀具尺寸等加工工况频繁变化［6］，这对刀具磨损的精确预测提出了更为严峻的挑战。因此实现变工况的刀具磨损精确预测具有重要的实际意义。除此之外，刀具磨损预测在制造系统中属于风险敏感的任务，这意味着预测结果与真实结果之间不容许出现较大的偏差，尤其在面对航空航天领域的高附加值零件时［7］。预测磨损量远高于真实磨损量将导致刀具的频繁更换，造成刀具使用寿命的浪费以及加工效率的降低。而预测磨损量远低于真实磨损量将出现使用失效刀具加工零件的情况，损害零件尺寸精度和表面质量，甚至造成零件报废。因此，有效的刀具磨损预测模型不仅需要保证预测的平均精度，还需要保证预测的稳定性，避免在加工过程中出现较大的预测偏差。

1 现有刀具磨损预测方法

现有的刀具磨损预测方法大多仅通过磨损机理或监测数据建立模型，受制于磨损过程的复杂性和模型训练数据获取困难等问题，难以实现变工况刀具磨损的精确稳定预测。数据与机理融合模型具备机理模型和数据驱动模型的优势，是实现刀具磨损预测的有效手段，然而现有的融合方法在模型训练过程中难以有效平衡对数据和机理的利用，导致融合效果不理想，因此亟需一种新的融合模型以满足精度高、稳定性好的预测要求。

现有的刀具磨损预测研究主要分为3 个方面：基于磨损机理的预测方法、数据驱动的预测方法和数据与机理融合的预测方法。

（1）基于磨损机理的刀具磨损预测方法

基于机理的刀具磨损预测方法通过分析刀具在切削过程中发生的物理变化（磨粒磨损和粘结磨损）和化学变化（扩散磨损和氧化磨损），构建刀具磨损量与各物理变量之间的关系公式。Takeyama和Murata［8］介绍了一个通用表达式，用于描述刀具磨损随时间变化的复杂过程。Pálmai［9］在建立机理模型过程中同时将机械磨损与化学磨损纳入考虑，提出一种刀具后刀面磨损速率的数学模型。Rech 等［10］使用摩擦计模拟在刀具-工件界面上的相关摩擦条件（压力，速度），改善了有限元分析刀具磨损的数值模型。机理模型可以很好地反映刀具磨损的规律，对于不同的切削过程具有较高的物理一致性，因此泛化性和稳定性较好。但机理模型的建立基于大量的假设和简化，对于复杂的切削过程，其难以实现刀具磨损的实时精确预测。

（2）数据驱动的刀具磨损预测方法

数据驱动的刀具磨损预测方法通过监测信号（如切削力信号，振动信号，声发射信号、主轴电流信号以及主轴功率信号等）间接反映刀具磨损状态［11］。近年来，随着数据获取成本和计算成本的降低，深度学习得到了快速的发展。在制造领域，深度学习为解决实际生产制造中的各种复杂问题提供了高效的解决方案［12-13］。Cai 等［14］利用深度长短时记忆神经网络（Deep long short-term memory network，DLSTM）提取监测信号中包含的深层特征，并与加工信息结合形成新的输入进行刀具磨损预测。Huang 等［15］通过对刀具磨损原始监测信号进行时间序列重构，利用深度卷积神经网络（Deep convolution neural network，DCNN）实现了刀具磨损量端到端的预测。Yuan 等［16］提出了一个通用的、端到端的制造系统监测框架，通过融合多传感器监测信号实现了刀具磨损预测。深度学习方法直接利用原始监测信号预测刀具磨损量，这使得其能够更全面、深入地挖掘监测信号中的信息。但受限于制造系统中的数据稀疏，难以剔除环境噪声的影响和训练困难等缺点，深度学习模型的泛化能力和预测精度仍有待提高。

（3）数据与机理融合的刀具磨损预测方法

数据驱动模型和机理模型具有很高的互补性，将监测数据与磨损机理融合建模可在一定程度上避免二者单独建模的缺点而发挥二者的优点，实现刀具磨损预测。Wang 等［17］通过使用经验公式Δθ=CNm构建物理模型并与数据驱动模型共同训练，将二者的预测结果进行回归训练以获得最终的预测结果。Hanachi 等［18］将自适应神经模糊推理系统与经验公式x(t)=texp(A+Bt+Ct2)相结合，通过粒子滤波以概率的形式表示预测结果。数据与机理融合的方式是影响融合模型性能的重要因素，而现有的方法大多是将机理模型与数据驱动模型叠加构成一个新的预测模型，数据与机理之间关联较弱，难以有效整合各自的优势，因此预测精度较低，特别是在变工况预测的情况下。

由于刀具切削过程的不确定性和磨损过程的复杂性，现存的磨损机理仅能近似表达刀具磨损的规律。因此对于刀具磨损融合预测模型，数据与机理的融合不应过于简单直接。一种较为可行的方法是以数据驱动模型为主体，通过将含有物理知识的惩罚项引入模型损失函数以约束模型的求解空间，如图1 所示。图中：hstart表示模型的初始状态，hI表示模型通过经验风险最小化获得的解（在有限的数据下获得的最优解），h*表示模型通过期望风险最小化获得的解（在无限的数据下获得的最优解），H表示模型的解空间，H′表示在磨损机理约束下模型解空间，Eest表示模型hI与h*预测误差的差值。

图1 机理约束数据驱动模型解空间Fig.1 Solution space of data-driven model constrained by mechanism

Raissi 等［19］提出一套模型融合框架，被称作Physics-informed neural networks（PINNs），用于求解偏微分方程的正问题和逆问题。在这套框架中，微分方程的解被表示成一个神经网络，将微分方程及其初始条件和边界条件引入网络训练的损失函数，从而约束网络参数的搜索空间。受此方法的启发，利用刀具磨损机理来约束数据驱动模型的解空间是一种有效手段。然而在构建PINN 融合预测模型时，数据驱动模型受到变工况下数据分布变化的影响，磨损机理也由于存在大量的近似简化，不能精确描述刀具磨损过程，这意味着并非所有的监测数据和磨损机理对建立准确的刀具磨损预测模型都能起到积极作用。而现有基于PINN 的数据与机理融合预测模型难以有效区别利用二者所提供的信息以实现监测数据与磨损机理的有效融合，因此难以实现变工况下刀具磨损的精确稳定预测。

针对上述问题，为了提高变工况下刀具磨损预测的精度和稳定性，本文在建立基于PINN 的刀具磨损融合预测模型的基础上，提出了一种基于元学习的模型优化方法，以实现变工况下的刀具磨损精确稳定预测。

2 基于元PINN 的数据与机理融合刀具磨损预测方法

2.1 方法介绍

数据驱动的和基于机理的刀具磨损预测方法均有各自的优缺点，数据与机理融合方法是整合二者优点同时避免二者缺点的潜在方案。针对在刀具磨损预测中数据与机理难以有效融合的问题，本文在建立了基于PINN 的刀具磨损融合预测模型的基础上，提出了基于元学习的刀具磨损融合预测模型优化方法，通过鲁棒性损失函数和极大似然估计推导出融合模型损失函数的加权形式以更合理地利用数据和机理，进而使用元学习算法学习损失函数参数和模型参数，让模型整合从不同工况数据中学习到的知识，提高模型的泛化性能，从而获得一个能够快速适应新工况的预测模型。

2.2 基于PINN 的刀具磨损预测模型

神经网络具备强大的拟合能力，可以拟合任何非线性函数［20］，但同时也意味着其庞大的搜索空间容易导致寻优困难。因此，为神经网络设置合理的约束是有效利用其拟合能力的有效手段。为了解决利用深度神经网络拟合监测信号与刀具磨损量之间复杂映射关系过程中的寻优困难、训练样本需求大的问题，本文将刀具磨损过程的物理变化规律作为先验知识，利用其约束预测网络的求解空间。对于磨损机理的研究，相关研究人员已总结了大量经验公式和领域知识，式（1）是对刀具磨损阶段划分规律的最佳匹配模型［9］。

式中：VB 表示刀具后刀面B区域最大磨损带宽；t表示磨损时间；a、b、c1、c2均为常数。

图2 基于PINN 的监测数据与磨损机理融合预测模型Fig.2 Prediction model of monitoring data and wear mechanism fusion based on PINN

为了将刀具磨损机理公式与现有刀具磨损数据集中的数据相匹配，本文将磨损机理式（1）作为与监测数据融合的磨损机理，提出基于PINN 的监测数据与磨损机理融合模型，如图2 所示，将机理公式作为神经网络损失函数的正则化项，约束模型的解空间，从而提高模型的预测精度和稳定性。图2 中：θ为神经网络参数；t为切削时间输入；xi为监测信号输入；a为神经网络中间状态值；θ*为优化获得的神经网络参数。

将磨损机理式（1）作为神经网络的正则化项加入模型的损失函数中以构成物理约束，视为物理损失，有

式中：θ表示模型参数；λ表示微分方程式（1）的参数，即λ={a，b，c1，c2}。∂ŷ ∂t表示模型预测的刀具磨损量ŷ对磨损时间t的偏微分。物理损失的构建基于以微分方程形式表达的磨损机理公式，由于机理式（1）只与磨损时间相关，因此无边界条件用于构建物理约束，而磨损机理的初始条件为：磨损时间为零，刀具磨损量为零，这可以体现在数据部分的损失项中，因此无须再构建初始条件的物理约束。将刀具磨损量预测误差视为数据损失，有

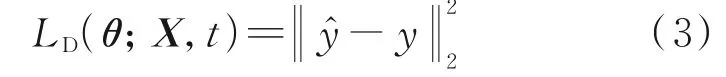
式中：y表示刀具磨损量标签值，物理损失和数据损失共同构建模型总的目标函数

2.3 基于元学习的刀具磨损融合预测模型优化方法

融合模型的求解问题属于多目标优化问题。大量研究表明，对于多目标优化模型，模型训练过程中对各个目标的平衡直接影响着模型的收敛速度和整体性能［21］，特别是当各个目标对模型整体性能贡献不确定时。因此本节考虑通过为融合模型损失函数加权的方式来合理利用监测数据与磨损机理，以最大化它们对模型性能的贡献。简单的做法是将损失函数的多个组分进行加权求和，通过手动试错的方式寻找各组分权重的最佳组合，即

式中：Ltotal为模型总的损失函数；Li为模型各部分损失；λi为各部分损失的权重系数。

然而这种做法明显的缺陷在于各组分权重的组合数量十分庞大，并且权重变化与模型性能之间的关系不一定是线性单调，因此难以寻找到最优的权重组合。特别是当损失函数组分较多或权重调整划分的粒度较小时，使用这种方法需要消耗大量时间和计算资源。基于以上认识，本节考虑让模型自适应优化各部分损失的权重参数，即

式中：λD、λP分别为数据部分损失和机理部分损失的加权参数，r(λD，λP)表示针对参数λD、λP的正则化项。引入可训练变量λD、λP对模型两项损失进行加权是平衡损失，区别利用两部分信息的初步设想，但简单引入可训练变量λD、λP训练模型缺乏理论依据，可能导致模型在训练过程中不收敛，从而无法达到预期效果。因此，文中基于一种鲁棒性损失以及极大似然估计推导给出融合模型损失函数合理的加权形式。而后针对变工况环境下预测模型的泛化性问题，对现有的元学习算法进行了适当的改进，使模型能够从不同工况数据中学习到更准确的融合规律，提高模型的预测精度和稳定性，其思路如图3 所示。图3中参数含义同图2。

图3 基于元学习的刀具磨损预测模型优化思路Fig.3 Optimization method of tool wear prediction model based on ML

2.3.1 融合模型损失函数设计

对于损失函数加权问题，Barron 在文献［22］中提出的自适应鲁棒损失函数具有一定的参考意义，有

该损失函数由a、c两个主要参数控制，其中a∈R，控制损失函数对监测数据中离群样本的鲁棒性，c＞0 控制了预测残差ε在零附近的聚集程度。当参数a为特定值时，式（7）所展示的损失函数将退化为或逼近特定的损失函数，如均方根误差损失函数，平均绝对误差损失函数等。

自适应鲁棒损失具有较好的性质，其对残差ε、参数a、参数c均是可导的，并且损失函数对残差ε的偏导数恒大于等于零。因此使用梯度下降算法对使用该鲁棒损失的模型进行优化是一种合理的手段。另外，由于损失函数对参数a的偏导数恒大于等于零，因此模型如果单纯使用式（7）所表示的损失函数将会使得参数a不断减小以降低损失值，这会导致模型不能专注于降低预测误差。针对以上问题，可以从极大似然的角度给出模型损失函数更为完善的形式［22］。式（7）所表示的损失函数对应的概率密度函数为

通过负对数极大似然变换，可以得到自适应鲁棒损失函数的完善形式为

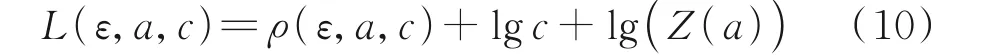
式中ε=y-f(θ，X)。因此损失函数可改写为

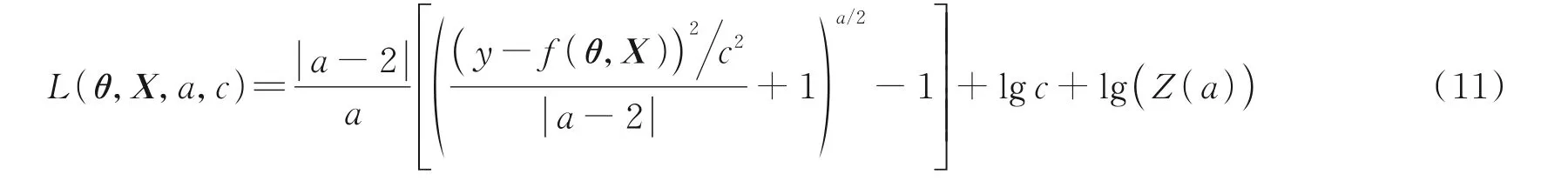
本文提出监测数据与磨损机理融合的刀具磨损预测模型为一个多目标优化模型，用f1(θ，X，t)表示模型输出的磨损量，f2(θ，X，t)表示输出对时间输入t的导数，即

由于f2(θ，X，t)表示模型输出f1(θ，X，t)对时间输入t的导数，f2(θ，X，t)仅与输入（X，t）相关，与输出f1(θ，X，t)无关，因此，可以将多目标似然函数进行分解为

因此，模型总的损失函数可以表示为

通过最小化模型的损失函数来训练模型来获得模型的参数。在训练过程中，神经网络参数θ，以及损失函数参数λ={λD，λP}={{a1，c1}，{a2，c2}}均由网络从数据中自适应学习获得。由上文所述，参数a的变化可以调控模型对离群样本的敏感性，保证模型的鲁棒性。而参数c则可看作损失项的加权参数，当依赖监测数据的预测结果中存在大量噪声，即c1增大时，1c21减小，说明监测数据对模型准确预测刀具磨损贡献不大，此时模型对数据驱动部分损失的注意力降低，即降低对监测数据的置信度，这对于机理损失同理。损失函数的后两项则充当正则化项防止模型在训练过程中为了减小整体损失值而使损失函数参数单调变化，使模型忽略输入的作用，从而导致模型训练的结果不理想。

2.3.2 基于元学习的损失函数优化方法

由于本文方法旨在变工况场景下实现监测数据与磨损机理有效融合，从而达到刀具磨损精确稳定预测，因此为了让模型整合从不同工况数据中学习到的知识，提高模型的泛化性能，从而获得一个能够快速适应新工况数据的模型。本节在无模型元学习算法［23］的基础上做出针对融合模型的改进，通过内外循环交替训练模型。在外层循环中，模型学习损失参数λ以及元模型参数θ。在内层循环中，模型以元模型参数θ作为每个基模型参数θi的初始值，固定损失参数λ，通过若干次迭代更新基模型参数θi。

根据元学习算法的双层优化问题框架［24］，首先给出了针对本文问题的求解表达形式，有

基于元学习的融合模型训练算法如下：

对于内循环优化基模型参数θ′i，由于式（14）表示的损失函数对基模型参数可微，因此使用梯度下降更新基模型参数θ′i，当内循环迭代次数为1时，θ′i只将元模型参数θ作为初始值进行1 次更新获得，而当内循环次数大于1 时，θ′i作1 次更新后将其上一次更新结果作为下一次更新的初始值。对于外循环优化损失参数λ与元模型参数θ，式（14）表示的损失函数对λ、θ均可微，因此可同时使用梯度下降算法进行更新。

以上算法详细描述了融合模型的训练过程，当模型训练完成后，可以获得在所有训练工况数据上表现良好的模型初始化参数θ以及损失函数参数λ。当面对新工况的样本数据Tnew时，可以直接使用训练好的模型进行磨损预测，即

式中ŷ表示刀具磨损预测值。而当新工况中有少量带标签样本时，还可以使用这些样本对模型参数θ使用少量步骤的梯度下降进行微调，从而提高模型对新工况数据的适应性，即为元测试过程，基于元学习的融合模型测试算法如下：

3 实例验证与分析

3.1 验证设计

本文设计多组钛合金铣削实验采集铣削过程中产生的信号以及刀具磨损量标签。在此基础上对比融合模型和优化后的融合模型的预测精度和预测稳定性，以此验证本文所提出的数据与机理融合的刀具磨损预测方法的有效性。本文以通过域对抗方式训练的深度神经网络作为数据驱动模型［25］，将源工况由一个扩展到多个，在此基础上融合磨损机理进行对比验证。域对抗神经网络可以从原始监测信号中提取与刀具磨损量相关性强，与工况信息相关性弱的信号特征，更好地实现变工况刀具磨损预测。

3.1.1 实验设备与数据

图4 实验设备Fig.4 Experimental device

本文加工实验全程在DMG 80P 数控加工中心上完成，实验过程中使用传感器采集力信号、振动信号及主轴功率信号，整体实验设备及装置如图4 所示。力信号由Pro-micron 公司的Spike 测力刀柄进行采集，采集信号包括刀具主轴绕x轴的弯矩Mx、绕y轴的弯矩My和绕z轴的扭矩Tz。振动信号由KSI-108M500 加速度传感器进行采集，采集信号包括水平2 个方向的振动。力信号和振动信号通过NI-PXIe-1073 数据采集平台进行汇集。主轴功率信号作为机床内部PLC（Programmable logic controller）寄存器中的数据通过OPC-UA（OLE for process control-unified architecture）通信协议实时读取。上述几种信号数据通过1 套基于Lab-VIEW 开发的软件系统进行实时同步［26］，采样频率为300 Hz。因此，本文使用的监测信号数据为包含3 个通道力信号（主轴绕x轴的弯矩、绕y轴的弯矩和绕z轴的扭矩）、2 个通道振动信号（水平2 个方向的振动）和1 个通道主轴功率信号在内的6 个通道信号。刀具磨损标签值通过采用西尼科XK-T600V 工业无线显微镜（测量精度0.01 mm）进行测量，磨损值范围为0～0.3 mm［27］。将监测信号和磨损时间作为模型的输入，以刀具磨损作为输出进行训练，训练数据只需满足以上输入输出形式即可。为了使模型适用于目标工况刀具的全磨损周期，源工况的监测数据需要包含刀具的全生命周期的磨损数据。

为了验证本文所提出的方法在实际加工过程中应对多种工况变化的有效性，设计了包括切削参数变化、刀具直径变化和刀具材料变化在内的4 组铣削实验，铣削类型为型腔铣削，型腔的大小为60 mm×50 mm×20 mm（长×宽×深）。4 组实验数据对应的切削参数与刀具参数如表1 所示，工件材料均为TC4 钛合金。值得注意的是，在实际生产加工中，不同直径的刀具所适用的切削参数一般不同，所以刀具直径变化的同时往往也伴随着切削参数的变化。刀具材料变化在实际加工中也十分常见，相比于整体硬质合金刀具，高速钢刀具切削刃硬度和强度都更低，适用的切削参数就更小一些。

表1 切削参数与刀具参数Table 1 Cutting parameters and tool parameters

通过对监测信号进行时序采样，以576 个采样点为1 个采样周期获得1 个样本，样本的标签值通过线性插值获取。各个加工工况的样本数量如表2 所示。为了评估和优化模型的性能，每个工况都随机抽取60%的样本作为训练集，20%的样本作为验证集，20%的样本作为测试集。

表2 各工况样本数量Table 2 Number of samples of each cutting condition

3.1.2 模型训练设置

模型采用3 种工况数据进行作为源工况数据进行训练，1 种工况数据作为目标工况数据进行测试。数据驱动模型输入仅为从监测信号中提取的特征，融合模型在信号特征的基础上加入磨损时间以便融入磨损机理。通过手动试错的方式多次调整超参数，最终确定使网络性能达到最优的超参数为：梯度下降算法为Adam，每次迭代的样本批次大小为128，学习率为0.001，网络迭代次数为2 000次。模型只有在离线训练过程中需要耗费一定的计算资源和计算时间，在测试以及实际应用时效率较高。在加工过程中，模型能够保证刀具磨损量的在线实时预测。

3.2 验证结果与分析

3.2.1 性能评价指标

本文分别从预测精度和预测稳定性两方面验证所提出的方法的有效性，采用平均绝对误差（Mean absolute error，MAE）作为量化评价预测精度的指标

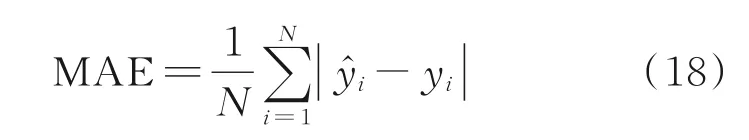
采用误差的标准差（Standard deviation，STD）作为量化评价预测稳定性的指标

式中εi=̂-yi表示预测误差。

3.2.2 融合模型优化验证

在PINN 的基础上，本文对模型的损失函数进行了合理的改进，采用元学习算法优化模型训练的过程，以提高融合模型的性能。为了验证对融合模型优化的有效性，本文对比了融合模型与元融合模型（Meta-PINN）的预测结果，如图5 所示。总体上，元融合模型在预测精度和预测稳定性上都优于融合模型。通过计算，元融合模型的MAE 与STD的都低于融合模型。在预测精度方面，元融合模型在4个工况样本上的平均预测误差MAE 为0.021 mm，而融合模型为0.031 mm，模型的平均预测精度提升了近32%。在预测稳定性方面，元融合模型在4种工况样本上的平均预测误差的标准差STD 为0.015 mm，而融合模型为0.018 mm，模型的平均预测稳定性提升了近17%。

图5 PINN 与Meta-PINN 预测结果对比Fig.5 Comparison of prediction results between PINN and Meta-PINN

为了更加直观且从细节上体现优化方法的有效性，给出了实际磨损曲线与模型预测磨损曲线，以及预测误差对比结果，如图6 所示。从图6 中可以看出，融合模型经过优化，预测误差的最大值大多都有降低，预测误差中大于0.05 mm 的样本数量基本都降低至10%以下，进一步验证了本文方法的实用性。

图6 实际磨损曲线与预测磨损曲线的对比Fig.6 Comparison between actual wear curves and predicted wear curves

4 结论

刀具磨损的精确稳定预测在航空航天制造中具有重要意义。数据驱动和基于机理的刀具磨损预测方法都由于自身存在的问题难以实现变工况的刀具磨损精确稳定预测，数据与机理融合方法具备机理模型和数据驱动模型的优势，是实现刀具磨损预测的有效手段。然而现有的融合方法在模型训练过程中难以有效平衡对数据和机理的利用，导致融合效果欠佳。针对以上问题，本文在建立了基于PINN 的刀具磨损融合预测模型的基础上，提出了一种基于元学习的刀具磨损融合预测模型优化方法，通过鲁棒性损失函数和极大似然估计推导出融合模型损失函数的加权形式以更合理利用数据和机理，进而使用元学习算法学习损失函数参数和模型参数，提高模型的泛化性能，从而获得一个能够快速适应新工况的预测模型，以实现变工况下的刀具磨损精确稳定预测。最后，方法的有效性在钛合金铣削实验数据集上进行了验证。本文的主要贡献在于：

（1）通过鲁棒性损失函数以及极大似然估计设计融合模型的损失函数，进而使用元学习算法优化融合模型的学习过程，提高了融合模型变工况下的预测精度和稳定性。

（2）实验结果表明，通过基于元学习的优化算法对融合模型进行优化，融合模型的预测精度和稳定性提高了32%和17%。

由于实验条件的限制，本文方法融合的机理为较为简单的刀具磨损经验公式，后续可针对更复杂的磨损机理设计相应的铣削实验，进一步提升融合模型的预测效果。另外，本文方法对工况范围有一定的要求，对于工件材料变化或切削参数变化更剧烈的工况，本文方法还存在一定的局限性，若要试图扩大适用范围，则需要采集更多变工况下的监测数据。