热流固耦合下T型管道疲劳分析

袁莹浩，丁新宇，白文婷*

(1.河北地质大学 城市地质与工程学院，河北 石家庄 050031； 2.北方工程设计研究院有限公司，河北 石家庄 050031)

在工程中，疲劳失效是结构中主要的失效问题[1]。尤其是在核电、化工等这种大型设施中，存在由管内流体温度场，速度场分布不均和管壁耦合作用导致的管道失效问题，是不可忽视的安全隐患。国内外对管道的热应力以及热疲劳现象研究多是基于实验与有限元数值模拟方法结合并进行对比，Gauder等[2]研究了湍流入口条件对核电站三通管道冷热混合特性的影响，其研究结果表明入流湍流对温度波动、湍流动能和温度-速度相关性等参数的评估有不可忽视的影响，而普通的流动条件没有引起近壁温度波动的任何主导频率。Boo等[3]利用计算流体力学与格林函数对核电站管道的局部温度和热应力进行了数值模拟分析，得出的流体温度也与实际设计的温度差别不大。其研究结果表明数值模拟在该问题上的可行性[4-7]，而且在大型特殊管道工程，有限元方法也能提供很好的预测。余志兵等[8]采用有限元分析软件，结合管-土相互作用参数，建立多跨海管数值计算模型，提出悬空管道模态分析方法并采用Miner线性累计损伤理论和S-N曲线对管道的疲劳寿命做出了预测。在疲劳领域中相关性分析仍缺乏，而在研究影响因素并揭示一般规律时，相关性系数是一个很好的度量指标。

本文通过引用皮尔逊相关性系数，对影响管道应力及其疲劳寿命的复杂原因进行了分析。T型三通管道在核电、化工、石油等管道系统应用广泛，且往往是管路系统中最为薄弱环节。在复杂工况的情况下，主支管可能存在不可忽视的温度差、速度差，在此期间存在冷热水的持续混合过程，产生交替变化的热疲劳载荷作用，在其作用下，管道可能产生热疲劳裂纹，甚至发展为贯穿裂纹，造成管道的失效。故选取一段三通管作为物理分析模型。

1 计算模型

1.1 数学模型

较于标准的K-Epsilon湍流模型，Realizable K-Epsilon模型能更好地体现管内旋转剪切流、含有射流和混合的自由流、管内流动的现象[9]，采用Realizable K-Epsilon湍流模型以及标准壁面函数的方法同大涡模拟相比，在保证计算精度的同时大大节省了计算资源，能更高效地研究T管中由于主支管射入流的温差以及速度差影响。

为研究流场内压强和速度与主支管温差和速度差之间相关性的强弱，引入了皮尔逊相关系数来判断其相关性。该系数是描述两变量间关系密切程度的度量指标[10]，其关系如下：

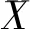
1.2 有限元模型

管道模型外径63 mm，壁厚4 mm，主管长度600 mm，支管200 mm。其中inlet1、2为进口，并将inlet2设为固定端，outlet为出口，控制进出口处管道的轴向位移为零，管道及有限元网格模型详见图1。

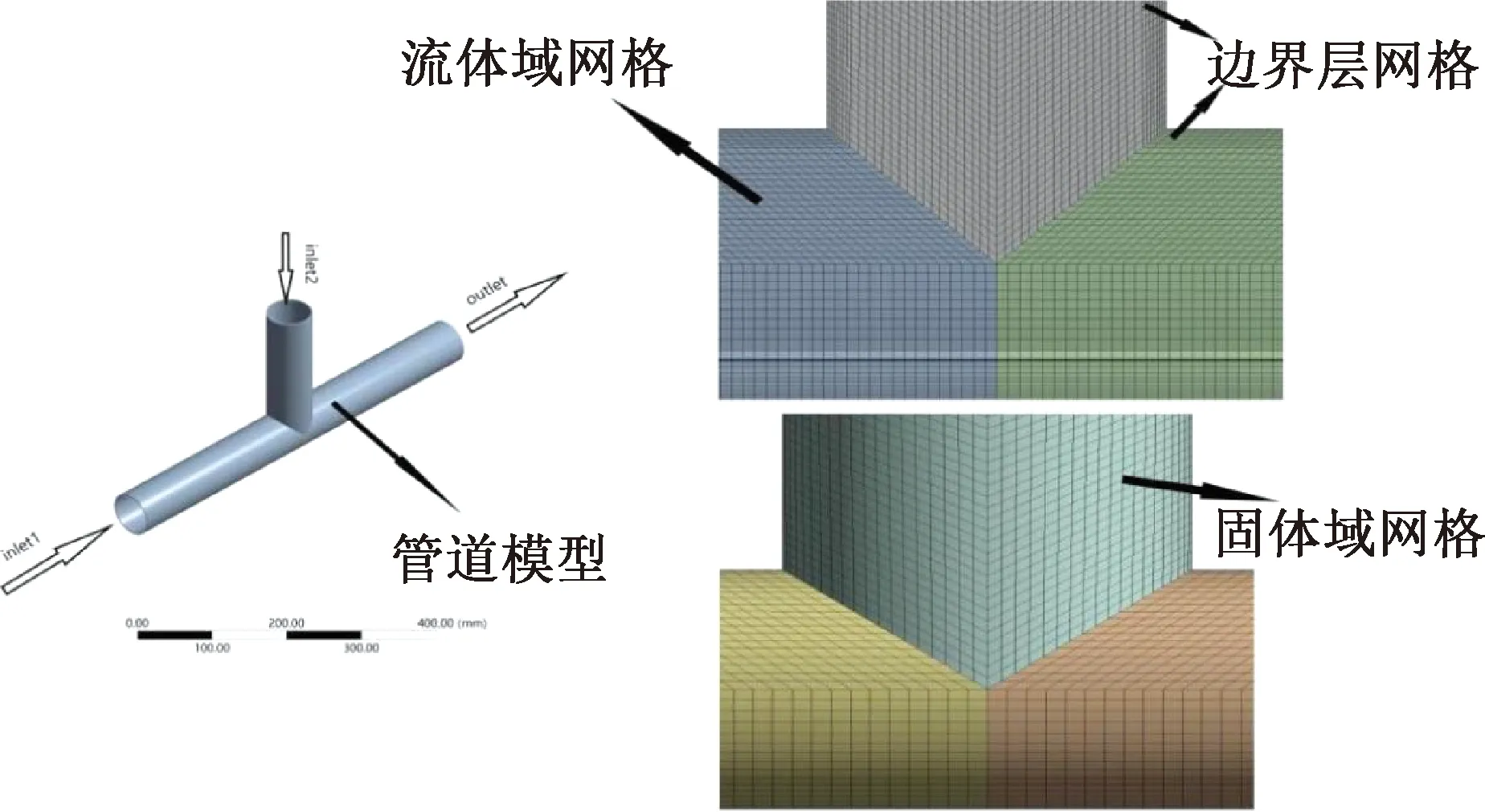
图1 有限元模型图Fig.1 Finite element model diagram

2 应力计算

2.1 工况设计

设计六组实验组，每组包含5种工况。第一组和第二组管道初始应力采用10.268 MPa，第三组、第四组9.651 MPa，最后两组设为9.270 MPa，以此来观察管道米塞斯应力随主支管温差以及速度差变化的影响。从第一组到第六组每组主支管的温差依次递减，递减梯度为20 ℃，且管道初始应力随着温度的升高也逐级减小；每组5种工况的主支管速度差依次递减，递减梯度为0.2 m/s，详见表1。

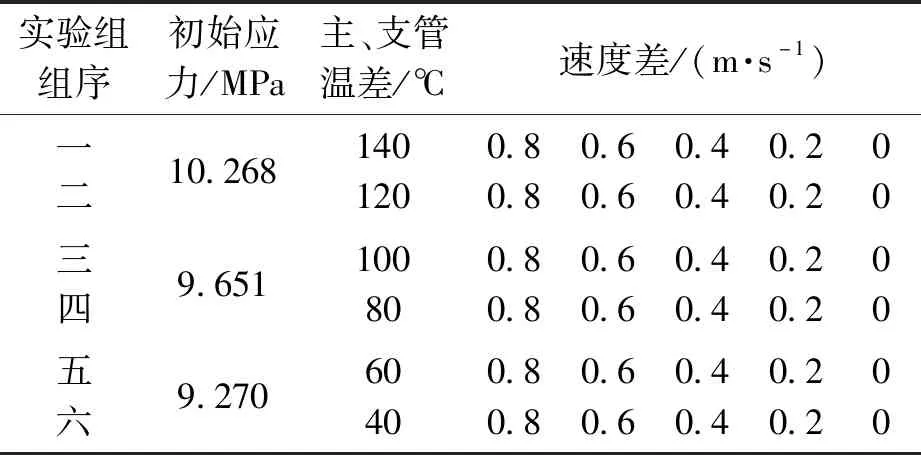
表1 工况Tab.1 Work conditions

2.2 计算参数设置

2.2.1 流场计算

流场域的具体边界条件详见表2，设定流体域壁层为绝热边界，热交换系数为0，出口表压为0，管道内壁面作为耦合边界。在计算过程中，考虑重力因素，将流体域设定成流动的单相液态水，使用FLUENT材料库中自带的WATER-LIQUID材料，采用Realizable K-Epsilon数学模型并打开能量方程，选择混合初始化，使用Couple耦合求解器与Second Order Upwind格式开始进行瞬态求解。为了更好地贴近实际情况，先计算一个极短的时间步，设定为1E-5 s，导出该过程中流体域的温度，压强等数值，再重新进行混合初始化，将导出的数据作为初始化的数据，进行瞬态计算。瞬态求解总时间为200 s，时间步长设定为0.05 s，数据监测频率为300 Hz。

表2 计算边界条件Tab.2 Boundary conditions of calculation

2.2.2 流固耦合计算

流固耦合分为单向耦合和双向耦合，在实际工况下，管道因流体作用导致的变形相对较小，对流场的影响可忽略不计，故选择单向耦合方法进行计算。其中固体域的边界条件详见表3。将在流体域计算得到的管道内壁面压强、温度作为瞬态载荷加载到固体域。

表3 流固耦合边界条件Tab.3 Boundary conditions of fluid-solid coupling

设管道的材料为304L不锈钢，密度为7 930 kg/m3，热膨胀系数设为1.84E-5/℃，杨氏模量为1.45E5 MPa，泊松比是0.3，采用双线性各向同性硬化曲线考虑材料的非线性。

3 结果分析

3.1 流场域分析

在FLUENT进行瞬态计算后，统计进出口流量，得到出口流量等于两个进口流量之和，故计算满足质量守恒定律，在管道的T型中央沿x轴轴向方向设置5个监测点，出口处每隔90度设置一个监测点，总共4个，见图2。为探究主支管温差，速度差对流场内速度和压强的影响，选择节点平均压强以及节点平均速度作为具体的指标来进行分析，结果见图3。监测点处的压强均值同主支管速度差具有明显的线性规律，并且六种线型几乎完全重合，表明流场的监测点处的平均压强和速度受温差的影响极小。

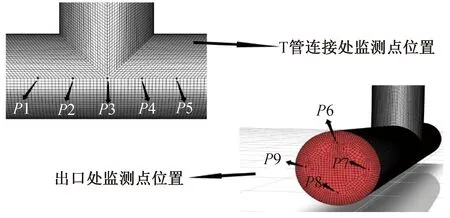
图2 监测点分布图Fig.2 Monitoring point distribution diagram

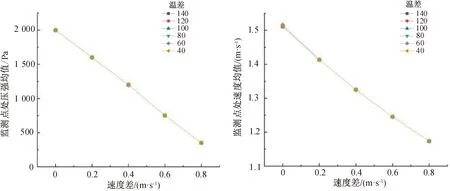
图3 计算结果图Fig.3 Calculation results diagram

引用皮尔逊相关性系数，直观地观察流场监测点处平均压强和速度与主支管速度差相关性的强弱。为方便分析，因出口处4个监测点表压为0，则只统计4个监测点速度的均值。计算结果见表4。从表中可以看出，皮尔逊相关性系数的绝对值均大于0.8，说明流场内压强和速度与主支管速度差高度相关，与上述分析一致。

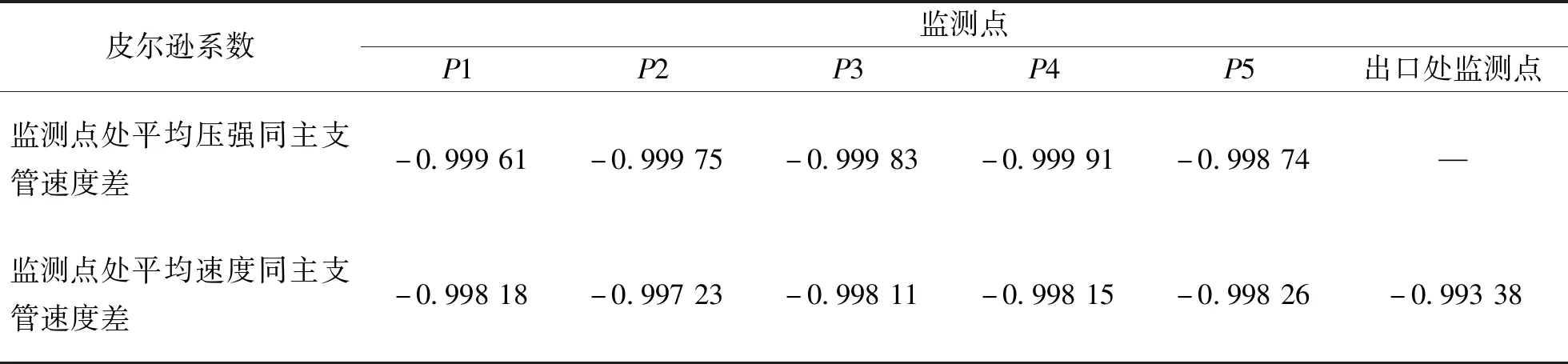
表4 监测点处皮尔逊相关性系数Tab.4 Pearson correlation coefficient at the monitoring site

3.2 固体域分析

在Workbench平台中，将流固耦合计算结果通过Static Structure模块施加到固体域，给定材料的导热系数15 W/m·℃，比热容500 J/Kg·℃。耦合计算时间共5 s，耦合计算发现，在初始应力，主支管速度差以及温差三个因素的共同作用下，管道最大米塞斯等效应力位置即管道危险处大致分为两种情况。

第一种情况：在第一、二和第五实验组所设置的工况下(在第三实验组中仅当主支管速度差在0.6及以上时)最大米塞斯应力位置出现在T型连接处即主支管冷热水交汇区域。米塞斯应力与主支管温差高度相关，与管道初始应力中度相关，同速度差弱相关，详见表5。说明在主支管温差较大情况下，管道最大米塞斯等效应力取决于管道内部冷热水的持续混合，产生交替变化的热疲劳载荷作用。在30种工况中选择第7种工况的米塞斯应力云图，详见图4。

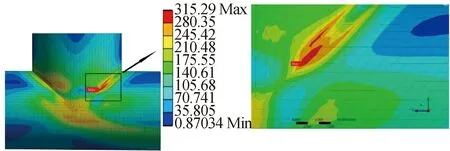
图4 管道T型连接处最大米塞斯应力云图Fig.4 Cloud map of the location of the maximum Mises stress at pipe T-junction

第二种情况：在第四和第六实验组所设置的工况下(在第三实验组中仅当主支管速度差在0.4及以下时)最大米塞斯应力位置出现在固定端附近且米塞斯等效应力和管道初始应力，温差中度相关(同管道初始应力相关性更高)，与速度差弱相关，详见表5。说明在管内的总温度逐渐上升之后，由于冷热水混合产生的热疲劳荷载逐渐减小，外部管道初始应力对管道的作用效果更为明显。在30种工况中选择第26种工况的管道最大米塞斯等效应力云图，详见图5。

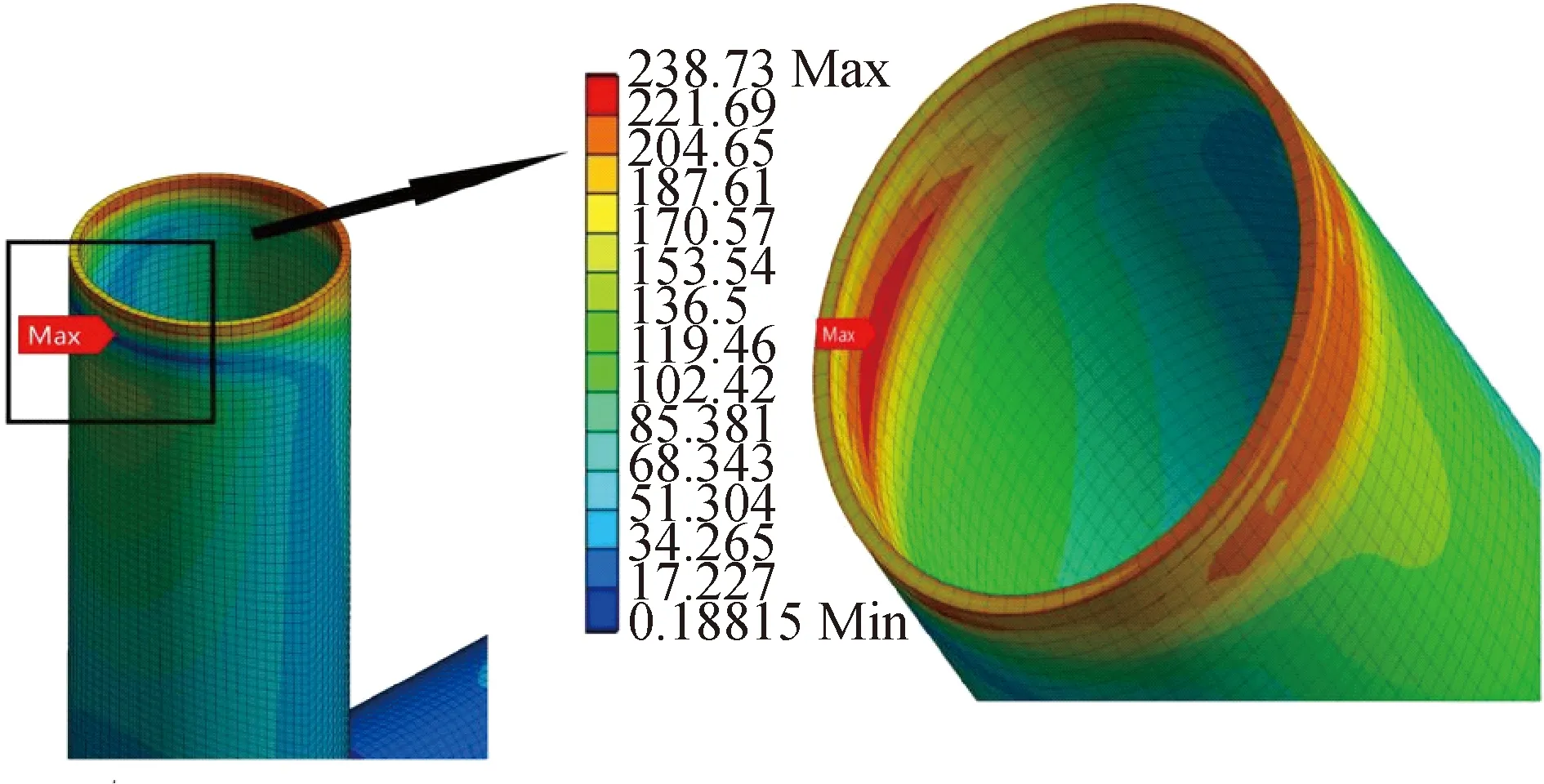
图5 管道固定端处最大米塞斯等效应力云图Fig.5 Cloud map of the location of the maximum mises stress at the fixed of the pipe

表5 皮尔逊相关性系数Tab.5 Pearson correlation coefficient

6组最大米塞斯等效应力大小详见图6。在第一、第二和第四实验组工况下，其最大米塞斯等效应力均普遍大于第三、第五和第六实验组，且第三组数据结果出现不单一性，原因在于当支管温度上升到60 ℃时，管内流体在该温差和速度差下未能充分进行混合，并且在管道初始应力外部作用的参与下，其复杂应力导致管道最大米塞斯等效应力和温差中度相关。大量实验数据表明，由于管道内流体平均温度的升高而产生的热应力对管道的作用远远小于冷热水混合产生的交变热荷载效应。

图6 每组等效应力图Fig.6 Equivalent stress of per group diagram

4 疲劳寿命预测

基于本文所采用的工况，管道受到的循环应力次数远远超过105，故属于高周疲劳，采用名义应力法对管道的疲劳寿命进行预测[11]，本文采用ANSYS自带的疲劳工具Fatigue Tool，疲劳强度因子(Kf)取1，载荷加载方式选择Fully-Reversed，见图7。放缩系数设置为1，应力通过Goodman曲线进行修正。

图7 荷载加载方式图Fig.7 Load loading method diagram

通过计算发现，不同工况下危险处的疲劳寿命与其最大米塞斯等效应力大小有直接关系，一般疲劳寿命最小处则为管道米塞斯等效应力最大处，计算结果详见表6。

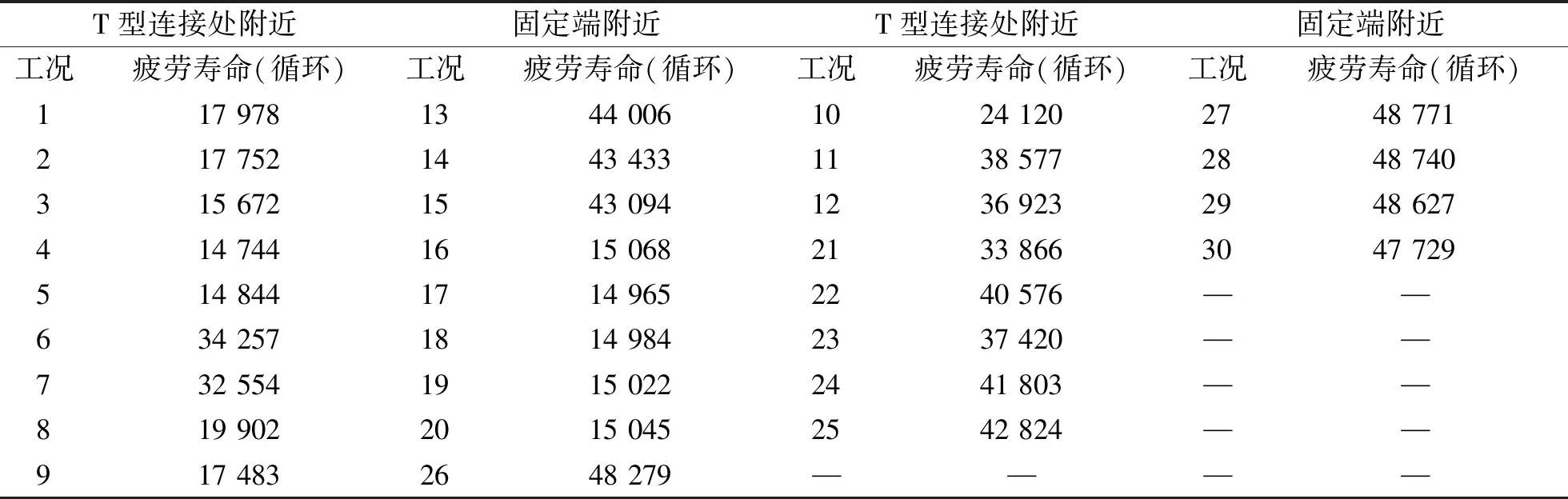
表6 疲劳寿命Tab.6 Fatigue life

对应上述热应力分析管道最大米塞斯等效应力位置出现的两种情况，分别引用皮尔逊相关性系数进行相关性分析得到：管道的疲劳寿命与米塞斯等效应力呈现极其显著的负相关，与计算结果吻合。当危险点出现在T型管连接处时，其疲劳寿命与主支管温差和管道初始应力高度相关(与温差相关性更高)，与速度差相关性弱相关；当危险点出现在固定端附近时，其疲劳寿命与管道初始应力，温差和速度差为中度相关(与管道初始应力相关性更高)，详见表7。

表7 疲劳寿命皮尔逊相关性系数Tab.7 Pearson correlation coefficient of fatigue life

5 结论

1)流场内的压强和速度主支管速度差高度负相关。

2)在管道初始应力，主支管速度差以及温差三个因素的共同作用下，管道危险处分别出现在T管连接处和固定端附近，第一种情况取决于管道内部冷热水的持续混合，产生交替变化的热疲劳载荷作用；第二种则取决于外部管道初始应力对管道的作用。

3)管道的疲劳寿命与管道最大米塞斯等效应力呈现高度的负相关。因管内流体平均温度的升高而使管道产生的热应力远远小于冷热水混合产生的交变热荷载使管道产生的热应力，控制主支管温差可大大减小因交变热荷载而导致T型连接处发生失效的概率，来延长管道的疲劳寿命。