新型互补序列设计及其在OFDM系统改进同步算法中的应用
2022-06-29张烁瑜高军萍
张烁瑜,高军萍,李 琦,王 丹
(河北工业大学 电子信息工程学院,天津 300401)
0 引言
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)系统虽具有抗干扰能力强、频谱利用率高的特点[1-4],但其对时间和频率偏移十分敏感[5-7]。在基于训练序列的同步算法中,最为经典的Schmidl 算法[8]由2 组相同序列构成,但该算法因循环前缀(Cyclic Prefix,CP)的影响而存在一段“平坦区”。Minn算法[9]将训练序列分为4部分,尽管该算法解决了“平坦区”的问题,但在定时估计曲线中存在一系列副峰,这会影响OFDM 系统的精确同步。Park[10]利用共轭对称结构提出一种新的算法,该算法的定时估计曲线在正确同步点有一个尖锐的峰值,同步较为准确,但副峰的存在仍可能会影响系统的正确同步。Schmidl、Minn和Park算法的训练序列均采用相关性较差的PN序列,而互补序列因具有良好的相关特性引起学者们的关注[11]。相比较于MPSK Golay 互补序列而言,MQAM 序列因其优良特性被更广泛应用于OFDM 系统中。Chong 和Tarokh[12]基于4QAM 序列,提出2 种16QAM Golay 互补序列的构造方法。2015 年,Zeng等[13]提出一种可将二元Golay互补序列直接生成16QAM Golay互补序列的设计方法。然而,目前互补序列的设计仍存在方法较少,长度受限的问题。
为提高OFDM系统的定时精度,本文利用相关性良好的新型互补序列对同步算法进行改进。首先,设计出一种新型16QAM Golay互补序列,该序列因具有良好的相关特性可以有效地应用于OFDM系统中;然后,利用新型互补序列和恒包络零自相关(Constant Amplitude Zero Auto Correlation,CAZAC)序列提出一种同步改进算法,该算法利用共轭对称结构,采用2组序列对原有的滑动窗口进行改进,通过对设计的2组窗口同时进行相关运算,可很好的解决系统在低信噪比下对定时偏移尤为敏感的问题。仿真结果表明,改进算法在低信噪比下仍可实现精准同步,并且副峰对主峰的影响较小,能够提高系统的定时精度。
1 新型Golay 互补序列的设计
由于OFDM 系统对定时偏移较为敏感,应用相关性良好的互补序列可以提高系统的定时精度。因此,本节提出一种新型16QAM Golay互补序列的设计方法,为互补序列在同步中的应用提供了更多的可选序列。
1.1 Golay 互补序列的定义
Golay[14]在1961年首次定义了Golay互补序列,通常采用自相关函数对其进行表征,定义如下:
定义1设序列u=(u0,u1,…,un-1),其非周期自相关函数为
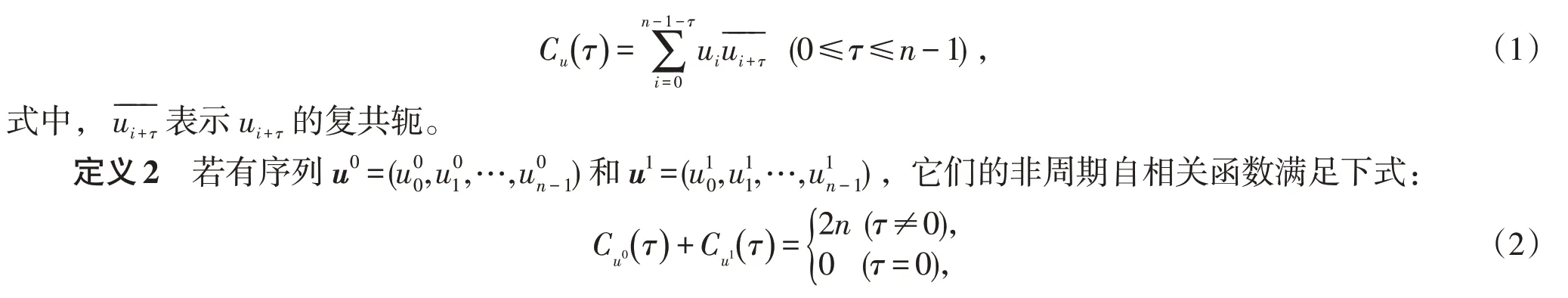
则称(u0,u1)为Golay互补序列对。
基于上述Golay互补序列对的思想,Tseng[15]提出Golay互补序列集,定义如下。
定义3若有m个长为n的序列(u0,u1,…,um-1)满足:

则称(u0,u1,…,um-1)构成一组Golay互补序列集。
1.2 新型16QAM Golay 互补序列的构造方法
首先,定义一组通过二元序列u0,u1得到十六元序列v0,v1,v2,v3的新型映射方法,如下:

新型16QAM Golay互补序列构造步骤如下:

步骤2利用式(4)所定义的新型映射关系,将序列(u0,u1)进行变换,可得到一组n长16QAM序列集(v0,v1,v2,v3)。
步骤3通过级联将(v0,v1,v2,v3)扩展成长度为2n的序列集(w0,w1,w2,w3),如下:

定理1如果存在一组n长二元Golay互补序列(u0,u1),通过式(4)变换得到序列(v0,v1,v2,v3),则该组序列(v0,v1,v2,v3)为Golay互补序列。
证明:根据自相关函数定义,

因此,
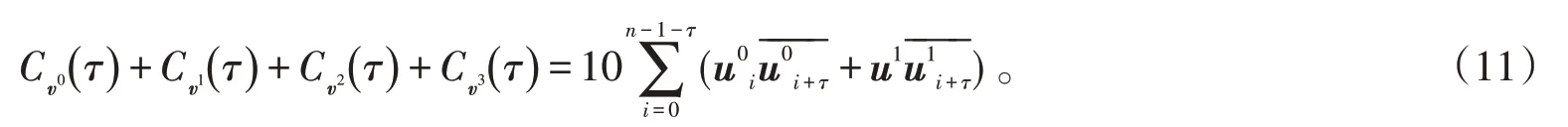
已知(u0,u1)为一组Golay互补序列,根据该序列自相关性质,可得

所以,

综上,(v0,v1,v2,v3)为Golay互补序列。
定理2若有一组n长Golay 互补序列(v0,v1,v2,v3),则其通过式(6)的级联方法所得到的序列(w0,w1,w2,w3)也为Golay互补序列。
证明:根据自相关函数定义,

同理可得,
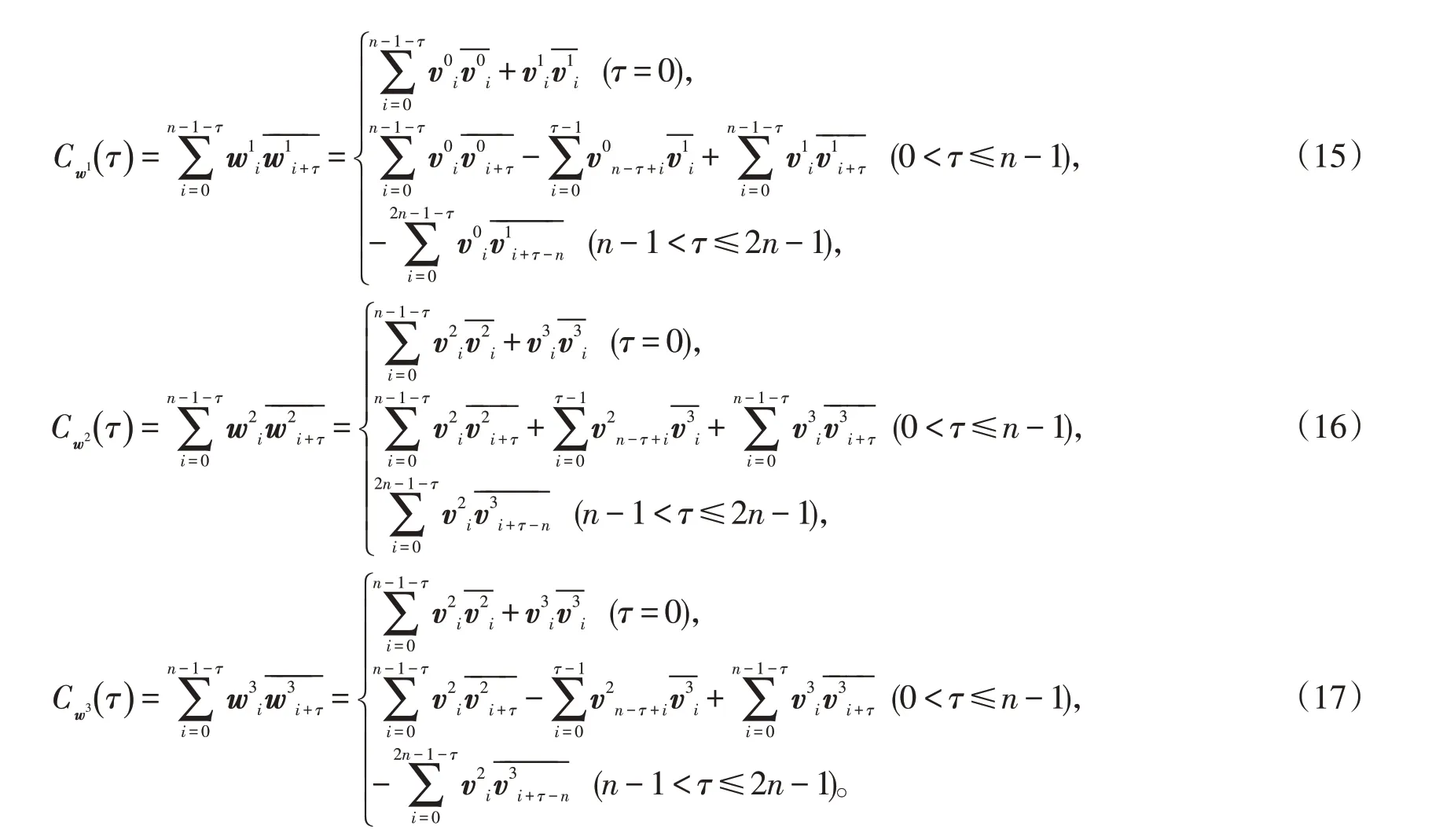
因此,

已证(v0,v1,v2,v3)为Golay互补序列,根据定义3可知:

因此,序列(w0,w1,w2,w3)为一组Golay互补序列。

证明:根据序列的自相关特性,


因此,推论成立。
表1对比了部分Golay互补序列的构造方法。现有的一些构造方法所设计的序列长度受限,仅能得到单一长度的序列,而本节提出的Golay 互补序列长度可根据初始序列长度和级联次数的不同,灵活得到多种可选序列。例如:若想得到长为16 的Golay 互补序列,利用本节提出的设计方法,可通过选取初始序列长度分别为2、4、8 的序列,并对应级联3、2、1 次的3种方法生成。另外,若想得到非2次幂长度的Golay互补序列,只需选取长度为非2次幂的初始序列并结合级联就可生成。

表1 Golay 互补序列构造方法对比Tab.1 Comparison of construction methods of Golay complementary sequences
1.3 构造实例
选取长度为4 的二元Golay 互补序列对(u0,u1),如下:

由式(4),可构造长为4的16QAM Golay互补序列(v0,v1,v2,v3):

利用推论中的方法,将(v0,v1,v2,v3)级联2次后,可得到长为16的16QAM Golay互补序列

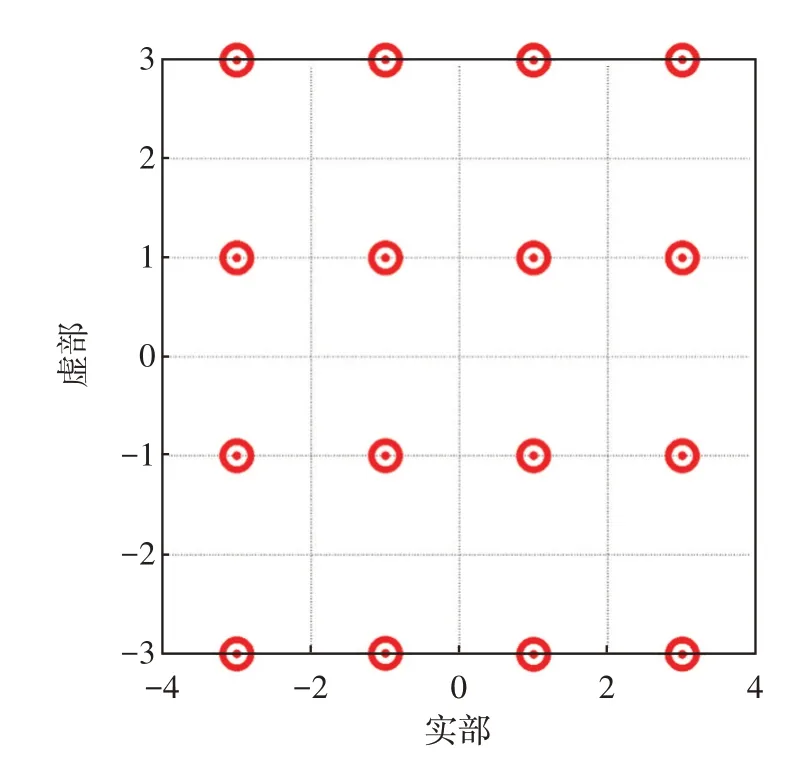
图1 星座图Fig.1 Constellation of sequence
2 新型互补序列在同步技术中的应用
由于OFDM 系统在低信噪比下对定时偏移更为敏感,本节通过对训练序列结构重新进行设计,利用新型16QAM Golay互补序列和CAZAC序列对滑动窗口进行改进,提出一种改进同步算法。
2.1 OFDM 系统同步原理
在含有N个子载波OFDM 系统中,信号采样值为[19]

图2 序列自相关特性Fig.2 Subsequence Autocorrelation Properties

式中:xn表示在第n个子载波上的传输信号;k为采样点。
若信号在接收端完成精准采样,则接收端的第k个采样值为

式中:θ为符号定时偏移;Δfc为归一化后的频率偏移值;n(k)为第k个采样值的加性高斯白噪声(Additive White Gaussian Noise,AWGN);接收信号y(k)由式(28)表示:

式中:L表示信道容量;h(l)为第l个信道的脉冲响应。
基于训练序列的同步算法的定时度量函数M(d)可由式(29)表示:

式中:P(d)表示滑动窗口的相关函数;R(d)表示接收机在滑动窗口d采样点时的能量。
2.2 基于新型互补序列和CAZAC 序列的改进同步算法
本节提出一种基于新型互补序列和CAZAC 序列的改进算法,该算法采用共轭对称结构,将训练序列分,4个部分:[A B*C D*]。其中,A是长度为N/4的互补序列,序列B为A的对称序列,C是长度为N/4的CAZAC序列,序列D为C的对称序列,符号“*”表示共轭运算,CP表示循环前缀,具体结构可表示为:
基于2 组不同的序列,改进算法分别利用2 个不同的滑动窗口进行相关运算。滑动窗口1 设置为互补序列,窗口2 为CAZAC 序列,且两窗口相距N/2。在该算法的窗口滑动过程中,只有当2个窗口同步点的相关值均为最大值时,所对应的才为正确同步点。为方便分析,将序列A,B*,C,D*分别表示为[a b],[b*a*],[c d],[d*c*],改进算法的滑动相关运算如图4所示:
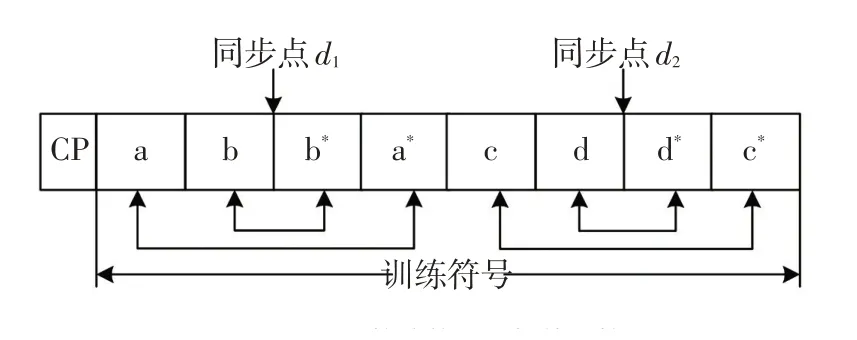
图4 改进算法的滑动相关运算Fig.4 Sliding correlation operation of proposed algorithm
由于改进算法利用2 个窗口进行滑动相关,根据训练序列的结构特点,该算法将2 个滑动窗口的Pi(d)和Ri(d)分别表示为
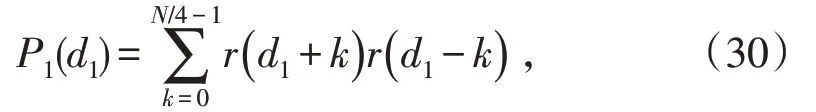

图3 改进算法的训练序列结构Fig.3 Training sequence structure of proposed algorithm


改进算法的定时度量函数表示为

式中:Pi(d)表示第i个滑动窗口的相关函数;Ri(d)表示接收机在第i个滑动窗口d采样点时的能量。
根据式(34)可知,当2 个窗口的定时度量函数为非峰值(即Mi(d)≠1)时,根据乘法运算的性质,改进算法的定时度量值接近于0,只有当2个滑动窗口的定时度量函数同时达到最大值时,此时才得到该算法定时度量函数的峰值。
改进算法的同步点置于训练符号起始位置N/4处,故定时同步点的估计值为

3 仿真结果分析
利用MATLAB 对OFDM 系统的几种不同算法:Schmidl 算法、Minn 算法、Park 算法以及改进同步算法,在低信噪比(Signal to Noise Ratio,SNR)下的定时估计曲线和峰值比进行仿真分析。
3.1 低信噪比下的定时估计曲线分析
图5 表示在CP=N/4,SNR=5 dB 条件下,4 种同步算法的定时估计曲线。图5(a)中,Schmidl 算法由循环前缀引起的“平坦区”会导致该算法无法进行准确同步;Minn算法在正确同步点位置附近存在着几乎与主峰等高的副峰,严重时,副峰值可能会超过在正确同步点处的主峰值,无法进行精准同步;在Park算法的定时估计曲线图中,虽然主峰尖锐,但由于循环前缀的存在,该算法的定时估计曲线在正确同步点附近仍会存在多个副峰;而在图5(b)改进算法的定时估计曲线中,几乎无副峰,仅在正确同步点处存在一个十分尖锐的峰值。仿真结果表明,改进算法在低SNR的情况下,主峰完全不会受到副峰的干扰,能够实现精确同步。
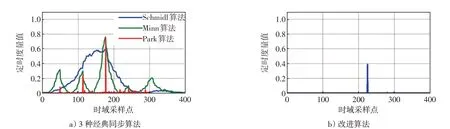
图5 4 种同步算法定时估计曲线Fig.5 The Timing Estimation Curves of Four Synchronization Algorithms
3.2 峰值比分析
副峰对主峰的干扰通常是影响OFDM系统正确同步的最主要原因,为直观描述这一特性,现将峰值比定义如下。
定义4将最高副峰幅值与主峰幅值之间的比值定义为峰值比,具体可用式(37)表示:

式中:P1表示最高副峰的幅值;Pm表示主峰的幅值。
图6所示为4种不同的同步算法在AWGN信道,CP=N/8,不同SNR条件下仿真500次时的Pr。从图中可发现,Schmidl算法、Minn算法受训练序列中的重复结构以及循环前缀的影响,其Pr较高;而Park算法虽较前2种算法而言Pr有所降低,但仍明显高于改进算法的Pr。根据式(37)可知,Pr越高,则说明最高副峰的幅值与主峰幅值之间差距越小,反之Pr越低,则说明最高副峰的幅值与主峰幅值相差越大。由此可见,改进算法的副峰对主峰的影响较小,有利于在OFDM系统中完成精准同步。

图6 4 种同步算法的峰值比Fig.6 Peak ratio of four synchronization algorithms
4 结语
由于OFDM系统对定时偏移较为敏感,互补序列因具有良好的相关特性可应用于该系统中。同时,为解决系统在低信噪比下仍存在定时精度差的问题,还需对系统中的同步算法进行改进。为此,本文首先提出一种新型16QAM Golay互补序列的设计方法,然后利用新型互补序列和CAZAC序列提出一种改进同步算法。该算法通过对原有的滑动窗口进行改进,采用2组滑动窗口同时对2组不同的序列进行同步,以此解决系统在低信噪比下对定时偏移更为敏感的问题。仿真结果表明,改进算法较经典同步算法而言,副峰对主峰的干扰较小,能够提高系统的定时精度。
