单双撑杆交错式索穹顶结构静力性能分析
2022-06-29张爱林袁文俊张艳霞朱莉娜熊家鑫
张爱林, 袁文俊, 张艳霞,2, 朱莉娜, 熊家鑫
(1. 北京建筑大学 土木与交通工程学院,北京 100044; 2. 北京建筑大学 北京未来城市设计高精尖创新中心,北京 100044;3. 北京工业大学 北京市高层和大跨度预应力钢结构工程技术研究中心,北京 100124)
索穹顶结构是一种构造巧妙、刚柔并济、轻盈优美的大跨度预应力结构,其来源于著名建筑大师Fuller的张拉整体思想[1]。Geiger[2]对“压杆孤岛处于拉杆海洋”思想进行适当的改造,设计了第一个索穹顶结构并成功应用于汉城奥运会的体操馆和击剑馆。Levy[3]进一步发展了索穹顶结构体系,改用联方型拉索网格,消除了Geiger型索穹顶的内部机构,并成功应用于亚特兰大奥运会主管场的乔治亚索穹顶。
张爱林教授创新研发了国内第一个大跨度索穹顶结构工程,并成功应用于内蒙古鄂尔多斯伊金霍洛旗全民健身中心[4-5]。其他学者也提出了许多新型索穹顶结构形式如:Kiewitt型[6]、葵花型[7-8]、鸟巢型[9]、蜂窝型[10-11]、倾斜撑杆式索穹顶[12]、联方型双撑杆索穹顶[13]、新型脊杆环撑索穹顶[14]、星型四面体索穹顶[15]。闫翔宇等[16-17]通过Levy式的过渡提出了外圈Levy式内圈Geiger式的复合式索穹顶方案,并成功应用于天津理工大学体育馆。受复合式索穹顶方案的启发,本文提出了一种单双撑杆交错式索穹顶,该体系采用单撑杆与双撑杆交替布置有效减少了索杆构件的数量,并对该结构进行了静力性能分析,研究了各种结构参数对结构刚度及承载力的影响,为结构的进一步设计提供了参考依据。
1 单双撑杆交错式索穹顶结构
1.1 拓扑形式
单双撑杆交错式索穹顶由环索、脊索、斜索、外拉斜索、撑杆、水平撑杆以及刚性环梁组成,结构示意图如图1所示。与传统Geiger型和Levy型索穹顶相比,从索穹顶中心到最外圈为单撑杆与双撑杆交替布置,并将竖直的单撑杆变为斜向撑杆,通过增设外拉斜索增加环向连接,同时最外圈双撑杆与水平撑杆首尾相接形成撑杆环,内圈双撑杆首尾相接形成撑杆环,提高了结构的环向刚度,增强了结构抵抗非均布荷载的能力。其中水平撑杆、斜索、脊索和斜向撑杆组成一个四面体,并且在水平投影中斜向撑杆和斜索分别为平面三角形的角平分线,同时平面投影还形成了7个全等的正六边形,从而保证了结构网格的均匀性,使结构整体性更好。
从上弦节点构件数、下弦结构构件数、每圈斜索数量、撑杆特点、水平投影特点等方面对单双撑杆交错式索穹顶和传统索穹顶的构件连接关系进行比较,如表1所示。与Geiger型索穹顶相比,单双撑杆交错式索穹顶最外圈为倾斜双撑杆和水平撑杆连接,增大了结构环向刚度,且水平撑杆的存在利于安装定位构件;与Levy型索穹顶对比,单双撑杆交错式索穹顶部分圈为单撑杆连接,在保证结构稳定性的同时可以达到节约材料的效果。整个单双撑杆交错式索穹顶杆的数量为49根,索的数量为126根,杆索数量比约为1∶2.57, Geiger型索穹顶杆索数量比约为1∶3,Levy型索穹顶杆索数量比约为1∶5。

注:HS-环索;JS-脊索;XS-斜索;WLXS-外拉斜索;CG-撑杆;SPCG-水平撑杆;GXHL-刚性环梁。图1 单双撑杆交错式索穹顶结构示意图Fig.1 Structural diagram of alternated cable dome with single and double brace struts
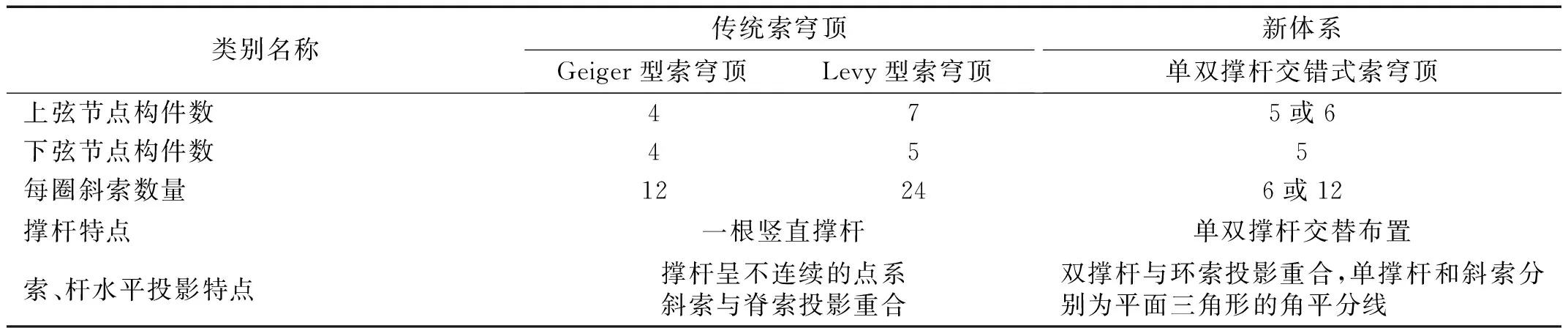
表1 构件连接关系对比Tab.1 Comparison of component connected relation
1.2 预应力简捷分析
单双撑杆交错式索穹顶结构为对称结构,取其1/6结构进行预应力分布计算,结构平面计算图和剖面计算图,如图2所示。为了在计算时书写简便:用Ci,Ji,Xi,Hi分别代表撑杆CGi、脊索JSi、斜索XSi和环索HSi的内力,i为不同的节点;αi为连接节点i与节点i+1的脊索与水平面的夹角,βi为连接节点i′与节点i+1的斜索与水平面的夹角,ξi为连接节点i与节点i′的撑杆与水平面形成的夹角,ψi,j为连接节点i与节点j形成的撑杆或索与对称轴线的夹角;hi为连接节点i与节点i+1在剖面图上的垂直长度,hi′为连接节点i′与其节点i+1的垂直长度。

图2 单双撑杆交错式索穹顶结构计算简图Fig.2 Structural calculation diagram of alternated cable dome with single and double brace struts

(1)

(2)

(3)
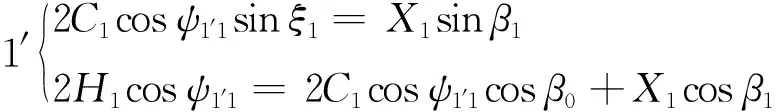
(4)

(5)
由于在节点0,1,0′,1′和2处一个节点均最多有两个未知力,可运用节点平衡法求解,但在节点2′存在多个未知力,属于超静定问题,无法利用普通的节点平衡法求解,此时引入位移法,以节点位移作为基本未知量,通过位移方程和已知外力,求出节点位移,进而推出索杆内力。将撑杆与索的单位刚度分别表示为(EA)V/li和(EA)T/lj,并假设单双撑杆交错式索穹顶在成形之后有足够大的刚度,节点2′产生小位移时不影响与各索杆另一端连接节点的位移,即假设各索杆另一端节点为铰接。以连接在节点2′上的各索杆作为分析单元,列位移方程。此公式仅适用于结构属于对称结构,外荷载也属于均布荷载时可用,式中:kxx,kyy分别为分析单元在x,y方向上产生单位位移时索需要的力;kx(y),ky(x)分别为当一个方向产生位移时,对另外一个方向的影响,则根据各索杆之间的关系,可得到式(6)、式(7)。
(6)
F2′x=C2cosξ2
F2′y=C2sinξ2
(7)
因为结构在成形后刚度足够大,节点2′在外力作用下产生的节点位移较小,可忽略当x(y)方向产生位移时对y(x)的影响,即kx(y)=ky(x)=0。求出每根索杆的单元刚度后,如式(8)、式(9)所示,然后联立式(6)、式(7)即可求得节点位移,进而求出节点上各索杆内力。
()()规定的范围内[8]。这说明所建立的发动机飞轮有限元模型能够较为准确地描述发动机飞轮的振动特性。
(8)
(9)
在节点3处,水平撑杆与对称轴线垂直,则其在对称轴平面投影为0,此时节点3处仅有两个未知力C3,J3,即可运用节点平衡法列出式(10)前两个平衡方程即可求解两个未知力,在求出这两个力后,结合平面图写出第三个平衡方程即可求出水平撑杆C33的内力。
同样节点3′属于超静定问题,利用位移法即可求得各索杆内力,H3与对称轴线垂直,故其在对称轴平面投影为0,利用位移法如式(11)、式(12)求解完其他索杆内力后,在利用节点平衡法如式(13)即可求得H3的内力。
(10)
(11)
(12)
通过式(10)~式(13)即可求出单双撑杆交错式索穹顶中的所有索杆内力,各索杆具体预应力大小及截面面积,如表2所示。
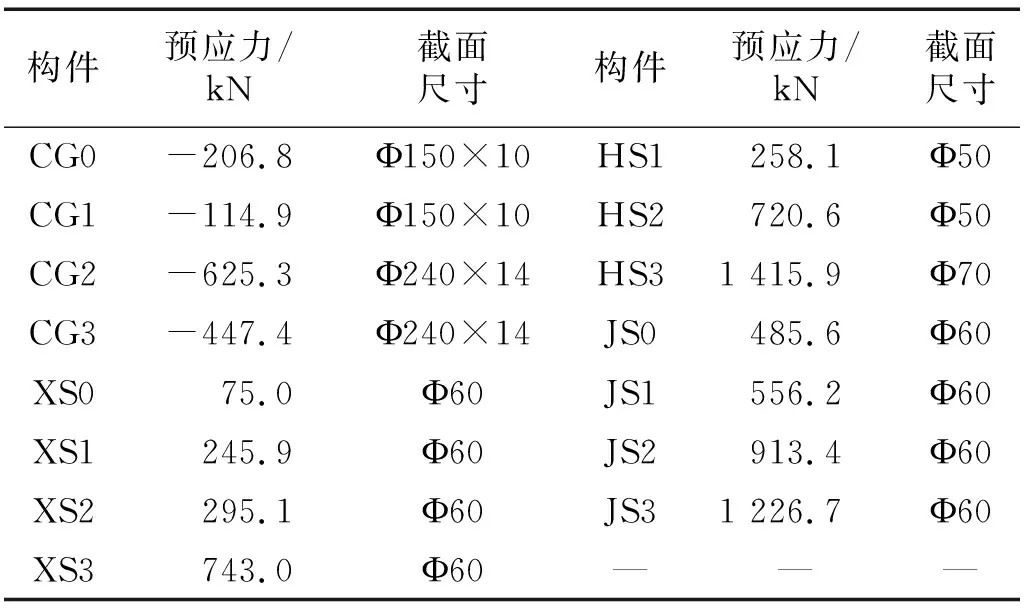
表2 计算模型截面和预应力设计Tab.2 Calculation model section and prestress design
1.3 分析模型
利用MIDAS软件对单双撑杆交错式索穹顶结构进行静力性能分析,选取静力分析模型跨度为60 m,矢高6 m,设置三圈环索,最内圈环索半径为9.8 m,第二圈环索半径为19.7 m,最外圈环索半径为26.2 m。撑杆采用Q355圆钢管,屈服强度为355 MPa,弹性模量为2.06×105MPa,采用桁架单元模拟,既能受拉又能受压。索采用钢铰线,屈服强度为1 860 MPa,弹性模量为1.95×105MPa,采用只受拉桁架单元模拟。屋面铺设膜材,采用平面应力单元模拟。
2 结构静力性能分析
对单双撑杆交错式索穹顶进行静力加载,膜材质量取0.1 kN/m2(不考虑膜材对结构刚度的贡献),屋面活荷载取0.5 kN/m2,研究均布竖向荷载分布形式对构件内力和变形的影响规律。工况一为在预应力状态下承受恒荷载和全跨均布竖向活荷载,全跨均布竖向荷载加载大小以0.6 kN/m2为荷载基础(1倍恒载+1倍活载),然后在该荷载基础上乘以荷载扩大系数λ,λ的范围为1~7,以每一级0.5的速率增加,在整个加载过程中,假设各索杆均处于弹性状态,且忽略自质量引起的拉索的垂度的影响。工况二为在预应力状态下承受恒荷载和半跨均布竖向活荷载,与全跨均布竖向荷载加载方式类似,考虑结构自质量,并在整个加载过程中施加0.1 kN/m2的恒荷载,然后在左半跨施加活荷载,活荷载基数为0.5 kN/m2。工况三为在预应力状态下承受1.3倍恒荷载和1.5倍全跨活荷载。工况四为在预应力状态下承受1.3倍恒荷载、1.5倍全跨活荷载和0.7×1.5×风荷载,北京地区50年一遇的基本风压为0.45 kN/m2。根据工程经验一般张拉完后索内力在0.2倍~0.5倍索破断力,所以取中值按0.35倍索破断力施加给环索,然后进行自质量和初拉力荷载共同作用下的荷载工况计算,看结构位移是否满足规范要求,如果满足,则将此初拉力荷载作用下的各索杆内力定义为1.0倍,如果不满足,则重新调整初拉力荷载的大小,直至结构位移满足要求。
2.1 全跨均布竖向荷载
图3显示了结构在全跨均布竖向荷载作用下结构的索杆内力变化和位移响应,由图3分析可知,随着λ的增加:①撑杆内力均不断增加,且从索穹顶中心到索穹顶外圈,撑杆内力不断增大,在6λ之前,撑杆内力呈线性变化趋势,在6λ之后,撑杆内力均出现转折点,同时上弦节点与下弦节点位移变化率增大,结构刚度降低。②斜索与环索内力均不断增加,内圈斜索和环索内力较小,外圈斜索和环索内力较大,环索内力在整个加载过程中都呈线性增加的趋势。斜索内力在6λ之前线性增加,在6λ之后,第二斜索XS2与外拉斜索WLXS内力出现拐点,外拉斜索内力降至0后失效,结构刚度降低。③脊索内力不断减小,相继出现拐点后失效。3λ之前脊索内力均呈线性减小的趋势,由于索穹顶外圈有刚性环梁,内环刚度相对较低,中心脊索率先失效,结构刚度降低,随着外荷载的不断增加,外圈脊索内力也不断减小,结构由内到外刚度不断降低。④上弦节点与下弦节点位移均呈不断增加的趋势,在6λ时由于大部分脊索均失效导致结构位移迅速增加并超过规范限值240 mm,说明对于该索穹顶而言外部荷载不宜大于6λ。
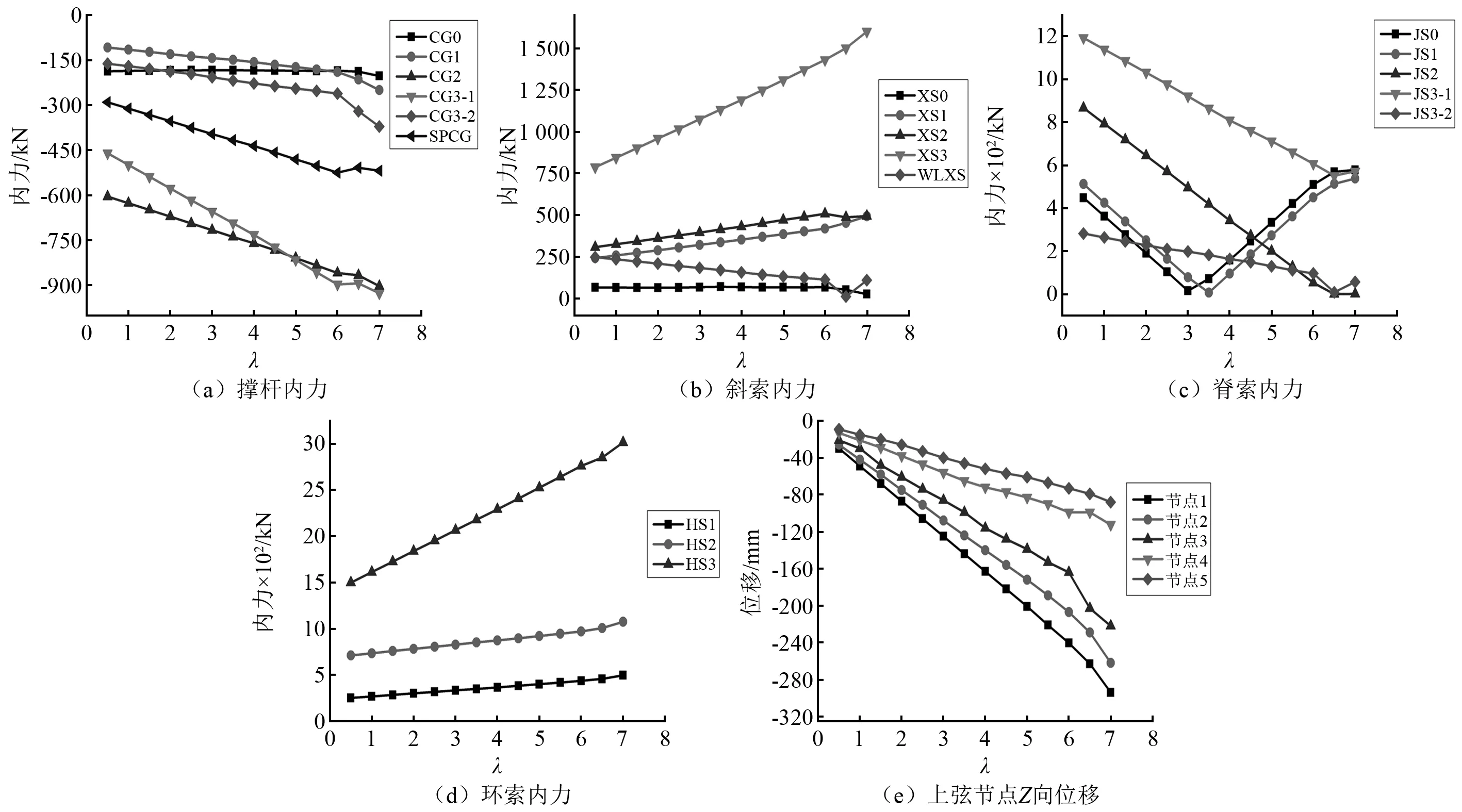
图3 全跨均布荷载作用下索杆内力和节点Z向位移Fig.3 Internal force of cable strut and Z-direction displacement of node under uniformly load of full span
2.2 半跨均布荷载
图4显示了半跨均布荷载作用下索杆内力变化和位移响应,由图4分析可知:①当荷载扩大系数λ≤2时,无论是有荷载跨还是无荷载跨,结构索杆内力以及节点Z向位移均呈线性变化趋势。对于有荷载跨,除部分脊索和外拉斜索内力呈减小趋势外,其他索杆内力均不断增加;对于无荷载跨,除少数撑杆、斜索、脊索、环索内力明显增加外,其他索杆内力均呈减小趋势。在半跨竖向均布荷载作用下,有荷载跨节点向下移动,无荷载跨节点向上移动,导致结构有荷载跨索杆内力和无荷载跨索杆内力变化趋势不一致。②当荷载扩大系数λ>2时,结构位移呈非线性变化趋势,且当λ=3时有荷载跨WLXS内力降至0后失效,结构刚度降低。随着荷载倍数的不断增加,内圈脊索内力斜索内力均不断减小,有荷载跨XS0内力趋近于0,结构刚度进一步降低。对于无荷载跨并未出现索失效的情况。③在半跨均布荷载作用下,结构同时出现向上、向下节点位移,节点向下最大位移点出现在有荷载跨第2圈撑杆顶点,节点向上最大位移点出现在无荷载跨第2圈撑杆顶点。④在半跨竖向均布荷载作用下,相较于全跨竖向均布荷载,有荷载跨各索杆内力均有不同程度增大,且竖向位移更大。满跨均布荷载作用下,结构变形均匀对称,而半跨均布荷载作用下,有荷载跨出现向下位移,无荷载跨出现向上竖向位移,结构变形不均匀,且两种工况下结构出现最大位移点的位置不同。随着全跨竖向均布荷载的不断增加,脊索由内向外逐渐失效,而对于半跨竖向均布荷载,内圈索几乎同时失效,对结构刚度影响较大,所以在结构设计时,应增加结构抵抗非均布荷载的能力,提高结构环向刚度。

图4 半跨均布荷载作用下索杆内力和结构Z向位移Fig.4 Internal force of cable strut and Z-direction displacement of structure under uniformly load of half span
2.3 风荷载
为了研究单双撑杆交错式索穹顶结构在风荷载作用下的响应,考虑了工况三和工况四两种荷载工况。等效静力风荷载大小按照GB 50009—2012《建筑结构荷载规范》[18]采用公式Wk=βZμSμZω0进行计算,其中:βZ为风振系数,对于柔性屋盖结构宜依据风洞试验结果按随机振动理论计算确定,本文暂取值为1.0;μS为风荷载体型系数,考虑到索穹顶整体较柔,取值为-1.0;μZ为风压高度变化系数,按建筑高度30 m,地面粗糙度B类,取值为1.39;ω0为基本风压,取值为0.45 kN/m2。由表3可知,结构在风荷载组合作用下相较于无风荷载作用时,脊索内力增大,其余构件内力减小,内圈脊索节点竖向位移最大,达到207.72 mm,满足结构变形要求。而无风荷载作用时节点竖向位移最大为166.68 mm,说明风荷载对于结构来说是不利荷载,且该结构在有风荷载作用时相较于无风荷载作用时位移增大了24%,说明该结构对于风荷载比较敏感。
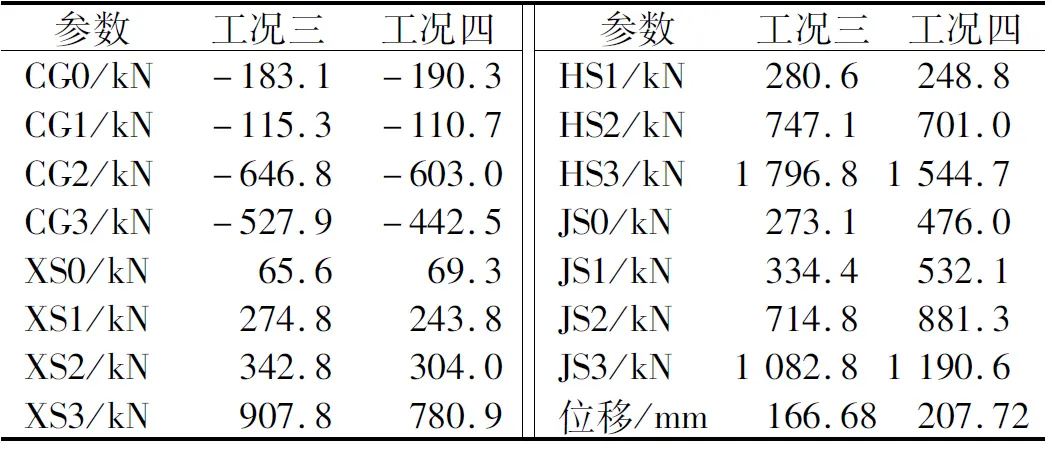
表3 两种工况下构件内力和结构最大位移Tab.3 Internal force and maximum displacement of components under two working conditions
2.4 自振特性分析
对结构进行了前50阶自振频率分析,从图5可以看出在前50阶频率中存在跳跃点,第一个跳跃点前的结构自振频率相差不大,第二个跳跃点前后的自振频率变化较大。结构1~5阶自振频率较密集,高阶自振频率较稀疏,说明结构低阶自振频率相近,高阶自振频率相差较大。表4为选取的较为典型的振型及其对应的自振频率。第1阶以外圈环向变形为主,内圈环向变形为辅,竖向位移较小;第10阶内圈环向变形稍大于外圈环向变形,同时也存在竖向位移;第12阶为纯竖向变形,结构中心位移最大,越往外圈结构位移越小。通过以上分析可看出,对于单双撑杆交错式索穹顶而言,其环向刚度稍弱于竖向刚度。

图5 结构前50阶自振频率Fig.5 The first 50 natural frequencies of the structure
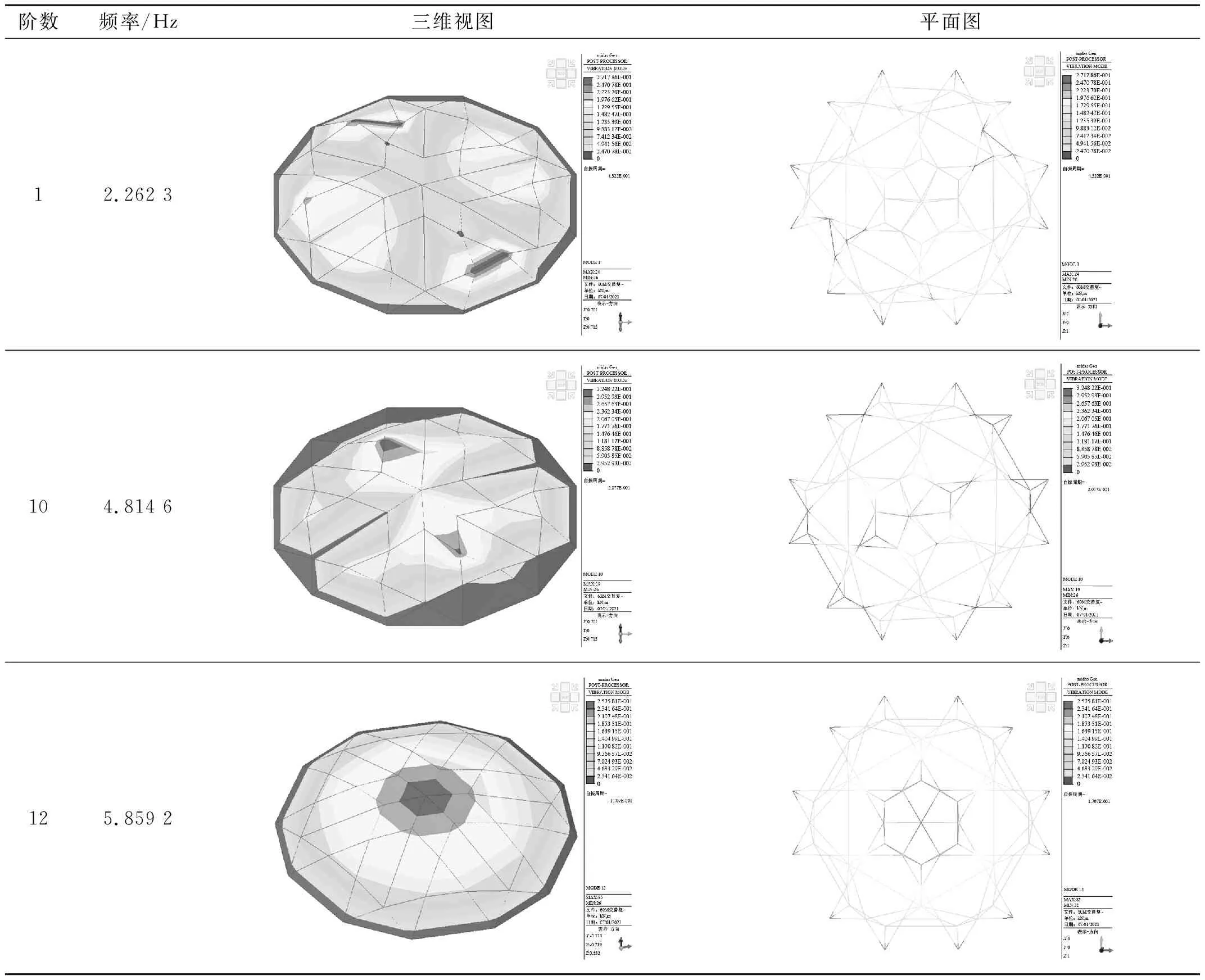
表4 结构自振振型及频率Tab.4 Natural vibration mode and frequency of structure
3 参数分析
在考虑结构自质量以及对结构施加1倍全跨均布竖向恒荷载以及1倍全跨均布竖向活荷载情况下,对结构进行参数分析,包括不同矢跨比、预应力倍数、撑杆高度对结构索杆内力及结构竖向位移的影响。
3.1 矢跨比
图6显示了结构在不同矢跨比时索杆内力以及上弦节点与下弦节点位移响应,矢跨比分别取1/8,1/10,1/12和1/15,由图6分析可知:①随着矢跨比的增加,撑杆内力、环索以及脊索内力均不断增加,内圈索杆内力变化较小,外圈索杆内力变化较大,中心脊索JS0与第一脊索JS1略有降低,其他脊索均不断增加。矢跨比从1/15到1/10各索杆内力的变化速率比矢跨比从1/10到1/8的变化速率大,说明适当的增加结构矢跨比可以提高结构刚度,过大的矢跨比对结构刚度的提高能力趋于饱和,优势不明显。②矢跨比越大,结构变形越小,上下弦节点位移越小,且由内向外节点位移逐渐减小。当矢跨比为1/15时节点位移为280 mm,超过规范限值240 mm,说明结构矢跨比不宜太小,矢跨比越小结构位移越大,构件变形越大,对实际工程中构件下料以及施工张拉不利。当矢跨比为1/8时,结构位移变化相对较小,且索杆内力优势也不明显,影响美观的同时还浪费材料,所以该结构矢跨比取值在1/12~1/10为宜,不仅能使结构有足够的承载力,同时还符合变形要求,节省材料方便施工,一举多得。
3.2 预应力倍数
图7显示了结构在不同初始预应力作用下结构索杆内力以及上下节点位移响应,由图7可知:①随着初始预应力的不断增加,各索杆内力均不断增加,但对内圈索杆的影响程度较小,对外圈各索力影响较大。内圈脊索、环索、斜索以及撑杆内力在3倍初始预应力时内力增加一倍多,但最外圈各索杆内力增加了3.5倍,最外圈环索内力值达到了4 200 kN,最外圈脊索内力值达到3 200 kN。适当增加初始预应力大小,可提高内圈索杆内力,从而增加结构内圈刚度,避免结构在较小外部荷载作用下,发生内索失效的现象,在1.2倍初始预应力时,结构刚度提高了27.7%,但同时也需注意初始预应力不宜过大,以防外圈索力超过破断索力,且预应力过大也会增加施工难度。②上下弦节点随初始预应力的增加而增加,在1.5倍初始预应力时,上下弦节点位移已经处于规范限值240 mm边缘,初始预应力继续增加,上下弦节点位移也不断增加,当初始预应力倍数达到3倍时,上下弦节点位移分别为562 mm和563 mm,此时节点位移为规范限值2倍多,同时过大变形不利于实际操作中张拉,所以初始预应力不宜过大,对于该索穹顶结构而言初始预应力在1.2倍~1.5倍合适。

图6 不同矢跨比时索杆内力以及节点位移响应Fig.6 Response of internal force and node displacement of cable strut under different rise span ratio
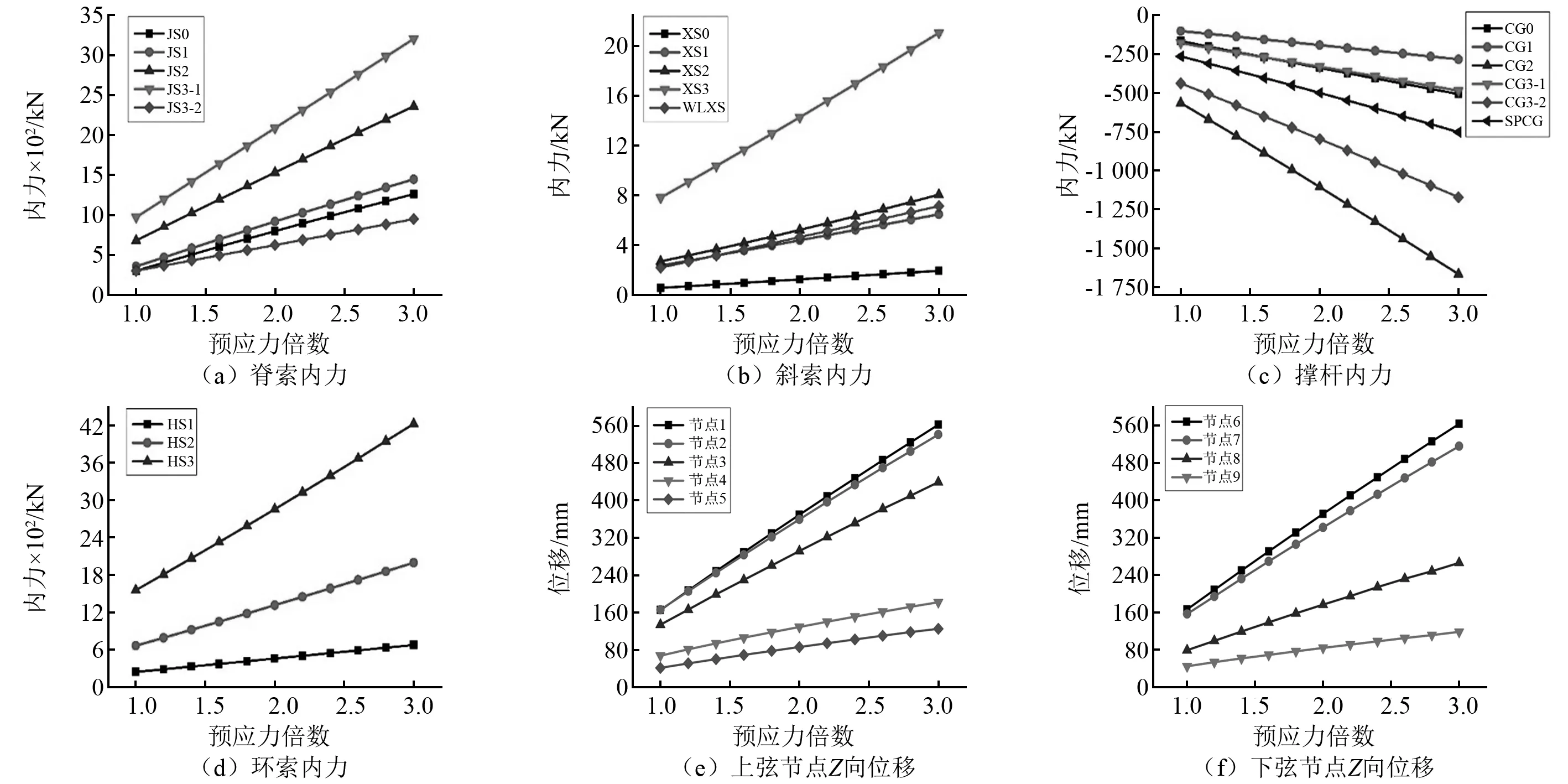
图7 不同预应力倍数下索杆内力以及节点位移响应Fig.7 Internal force of cable strut and displacement response of joint under different prestress multiple
3.3 撑杆高度
表5为各组撑杆高度,从第1组到第5组各撑杆高度逐渐增加,在改变撑杆高度时保持结构其他参数一致。从图8可得出以下结论:①在此种撑杆高度变化形式下,从整体上看,不论是各索杆内力还是结构上弦节点位移,均变化相对较小。②随着撑杆高度的增加,内圈撑杆内力有增大的趋势,但变化较为平缓,外圈撑杆内力在100 kN内变化;斜索内力与环索内力均不断减小,内圈斜索与内圈环索内力变化相对较小,外圈斜索与外圈环索内力变化相对较大,第5组撑杆高度所对应的斜索内力约为第1组撑杆高度的2/3,第5组撑杆高度所对应的环索内力也约第1组环索内力的2/3;内圈脊索内力随撑杆高度的增加而逐渐增大,外圈脊索内力随撑杆高度的增加而减小,变化幅度均相对较小。③从节点Z向位移图图8(e)可看出,撑杆高度的变化对节点位移影响较小,节点位移变化平缓,其中中心节点位移最大,外圈节点位移最小。

表5 各组撑杆高度Tab.5 Strut height of each group m
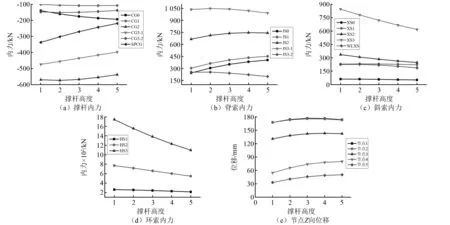
图8 不同撑杆高度下结构内力以及节点位移Fig.8 Internal force and node displacement of structure under different strut height
4 结 论
本文通过MIDAS软件分析了单双撑杆交错式索穹顶结构的静力性能。首先研究了在全跨和半跨竖向均布荷载作用下该结构的静力特性,然后通过改变矢跨比、预应力倍数、撑杆高度分析了该结构在不同参数条件下的静力性能响应,给出了各参数合适的取值范围,最后得到以下结论:
(1)单双撑杆交错式索穹顶结构上层脊索中同时存在索与撑杆,水平撑杆约束了脊索变形,增强了整体稳定性,内外圈撑杆形成两个闭合撑杆环,提高了结构抵抗非均布荷载能力。同时该结构平面投影形成7个全等的正六边形,结构网格划分均匀,结构整体性强。
(2)在全跨均布竖向荷载作用下索穹顶中心承载能力较低,中心处各索杆内力相对较小,在较大荷载作用下脊索容易失稳,因此中心脊索JS0首先出现索失效的现象。而在半跨均布竖向荷载作用下,结构产生水平位移,结构中部相对较薄弱,则结构中部的外拉斜索WLXS最先失效。
(3)结构矢跨比、预应力倍数和撑杆高度的变化均会对结构内力和节点位移产生影响,其中矢跨比影响最大,撑杆高度影响较小。矢跨比过大对于结构承载力提高不明显,过小会导致变形过大,故该结构矢跨比应控制在1/12~1/10。
(4)适当增大结构初始预应力可提高结构刚度,同时能防止张拉过程存在预应力损失而使结构实际没有达到1倍初始预应力,但初始预应力也不宜过大,会提高施工难度和对张拉设备的要求,故该结构初始预应力倍数宜控制在1.2倍~1.5倍。
(5)整个单双撑杆交错式索穹顶的杆索数量比大于传统Geiger型和Levy型索穹顶杆索数量比,且索材和圆钢管同等质量条件下的成本比例约为2.5∶1,因此单双撑杆交错式索穹顶造价有很大优势,具有应用前景。
