起重机载荷谱回归预测的LSSVM模型优化研究

于燕南， 戚其松， 董 青， 徐格宁

(太原科技大学 机械工程学院，太原 030024)

起重机作为一种特殊设备，是制造业的基础，支撑着国民经济的快速发展，其安全性至关重要。发达国家(如英国、德国、日本等)对起重机的生产均是以其安全性为主线，而我国目前实施的起重机安全试验，仅检测了起重机出厂状态的参数和性能，为保证起重机安全、稳定、长期可靠地运行，需要准确进行起重机金属结构疲劳剩余寿命评估和可靠性分析，真实准确地获取载荷谱是进行机械装备剩余寿命评估的前提[1-2]。国外的起重设备生产厂家在技术规格中提供了整机载荷谱，如美国Lifetech公司采用的是整机载荷谱估价法对起重机疲劳剩余寿命进行评估。但就目前而言，起重机载荷谱的编制原理和方法研究是起重机疲劳研究领域中的重点也是难点。国际上载荷谱数据和编谱方法实施细则属于机密和知识产权保护范围，我国针对起重机整机载荷谱的编制方法研究很少，所以，国内的起重机生产厂家无法提供起重机的载荷谱，因此需要加大在起重机载荷谱编制方面的研究力度。目前，获取起重机载荷-时间历程的方法共3种：第1种是对机械设备进行现场实际测量，该方法直接有效，准确性高，但因其周期性长且成本高导致推广性差；第2种是利用有限元仿真软件对起重机的实际工作状态进行模拟，该方法操作简单易实现，但因无法真实还原实际工作状况导致可信度低；第3种是通过现场实测和计算机仿真模拟相结合的方法，该方法结合了前两种方法的优点，可以更加准确有效地获取起重机的载荷谱，适合进行大范围研究和推广。

随着计算机技术的发展，智能优化算法结合机器学习技术成为预测领域的一大利器，在不同行业中得到了广泛应用。机器学习技术可以对现有的数据自动学习，由繁到简，发现并利用数据中的潜在规律，从而进行智能决策和判断，如：BP(back propagation)神经网络[3-4]，支持向量机(support vector machine， SVM)[5]，相关向量机(relevance vector machine, RVM)[6-7]等，国内外的许多学者利用这类技术在自己的研究领域取得了丰硕的成果：陆风仪等[8]从核函数的构造和决策函数两方面改进，验证了v-SVRM(v-support vector regression machine)预测模型在起重机载荷谱预测上具有良好的实用性和鲁棒性，但文中未涉及核参数优化选择的详细内容；徐格宁等[9]构建了结合粒子群和相关向量机的起重机载荷谱预测模型，克服了传统机器学习方法中欠学习、过学习、局部最优等现象，提高了预测精度；董青等[10]以具有混合核函数的相关向量机为基础，结合自适应步长果蝇算法，提出自适应双层果蝇相关向量机的起重机当量载荷谱预测方法，证明了该方法相比于其他方法，在预测精度方面的优越性；张小龙等[11]利用粒子群优化(partical swarm optimization,PSO)算法对支持向量机的参数作优化选择，并使用优化后的支持向量机对轴承振动信号样本进行故障类型的识别，获得了较高的识别准确率；刘伯颖等[12]建立的BAS-SVM(beetle antennae search-support vector machine)模型能有效缩短训练时间，收敛速度更快，且对IGBT(Insulated Gate Bipolar Transistor)结温的预测精度更高；王雪莹等[13]提出改进鸟群算法优化最小二乘支持向量机(least square support vector machine，LSSVM)模型，对锂离子电池剩余寿命进行预测，结果表明预测效果和稳定性良好；张永康等[14]运用混合人工蜂群和人工鱼群优化的LSSVM对脉动风速进行预测，与其他模型预测结果对比，混合优化算法优化的LSSVM模型精度较高，证明优化后的LSSVM可应用于实际脉动风速预测；温静媛等[15]将天牛须搜索算法与BP神经网络相结合，对深孔加工粗糙度作预测，达到了较为理想的效果，为深孔加工粗糙度研究提供了较好的思路；许景辉等[16]将传统天牛须搜索算法中的一只天牛改进为一个天牛种群，建立IBAS-BP 冬小麦根系含水率预测模型，可准确预测冬小麦根系土壤含水率，避免了网络陷入局部极小值的可能，具有较高的预测精度和鲁棒性；闫重熙等[17]引入模拟退火算法的蒙特卡洛法则，提出了一种天牛须搜索算法优化的LSSVM短期电力负荷预测模型，算法稳定性更高，并证明了该方法的有效性；Lin等[18]引入惯性加权策略和柯西突变算子，改进飞蛾优化算法,结合支持向量机进行光伏发电预测，减少光伏功率渗透到电网中的影响，保持系统的可靠性；Li等[19]使用混沌序列促进初始种群，引入动态递减步长因子，动态发现概率，动态惯性权重偏好随机游动和粒子群算法通信策略，提高了杜鹃搜索算法寻优效果，优化支持向量回归机的超参数，以法国风电场数据集为例，验证了其输出结果的精度和稳定性； Helaleh等[20]使用蚁群算法(ant colony optimization, ACO)优化支持向量机的参数选择，利用岩心驱油试验获取试验数据集，证明了ACO-SVM在不增加时间响应和计算时间的前提下取得了较高的精度；Rui等[21]通过比较SVM的3种模型参数选择方法(指定参数、网格搜索方法和粒子群算法)，发现粒子群算法在这3种方法中表现最好，表明智能优化算法在选择模型参数方面的优越性，因此利用线性递减惯性系数和变异粒子的粒子群优化算法优化支持向量机的高斯核函数参数的选择，实现对优质烃源岩的定性和定量评价；陈法法等[22]确立可靠性指标并构建相关向量机预测模型,准确预测了正在服役中的滚动轴承运行可靠度指标及其变化趋势;冯鹏飞等[23]建立特征指标与运行可靠性的关系，利用相关向量机预测对应的运行可靠度并分析航空发动机转子轴承失效时间，证明该方法的准确性;Xu等[24]建立了基于天牛须搜索算法优化反向传播神经网络的多因子预测模型，实现超参数的智能选择，提高了模型的计算效率和精度。

国内外的学者均利用机器学习和智能优化算法[25-28]等技术进行相关模型的预测和分析，此类方法正在成为预测这一科研领域的新潮流。目前，我国尚无公认的准确的起重机载荷谱预测模型，无法解决载荷在时间和空间上的随机性、间歇性及循环性的复杂非线性特征问题。一方面，考虑到LSSVM是专门针对小样本数据的回归预测的一种机器学习技术，在选取合适的参数后，比支持向量机、相关向量机、BP神经网络等在解决时间序列和非线性回归问题上具有更高的预测精度，计算速度也更快；另一方面，天牛须搜索算法具有原理简单、参数少、计算量少等优点，在处理低维优化目标时具有非常大的优势。故本文选择LSSVM模型预测起重机载荷谱，在选择核参数时，采用一种改进的天牛须搜索算法对LSSVM模型参数进行优化选择，试验证明，改进后的天牛须搜索算法(improve beetle antennae search,IBAS)可以快速自动选取到较优的LSSVM模型参数，使IBAS-LSSVM起重机预测模型在解决载荷谱回归预测问题上具有很好的预测精度和鲁棒性。

1 起重机载荷谱预测模型

通用桥式起重机在长期服役的情况下，主梁的疲劳性能会逐渐退化，最终发生疲劳断裂，造成灾难性事故。为了预防此类事故的发生，需要提前预测起重机的剩余疲劳寿命，科学理论表明，准确获取符合实际使用工况的载荷谱是确定剩余服役寿命的关键。

由于起重机实际工作载荷具有随机性、间歇性及偶然性，加上试验环境的局限性，导致大规模、等比例载荷谱试验难以实施，获取大样本载荷谱的代价很大且难以实现，为此提出“采集+预测”的方法，通过采集获取通用桥式起重机的小样本实测载荷谱，并将其作为LSSVM预测模型的输入，经过LSSVM预测模型对数据的统计学习和挖掘数据之间内在规律，形成数据之间的映射关系，输出与实际使用工况拟合度较高的载荷谱，将小样本扩展成大样本载荷谱，为预测疲劳剩余寿命奠定基础，从而评估起重机的安全性，提前实施相应的安全防护措施。

1.1 获取小样本载荷谱

针对特定的通用桥式起重机，测量其正常工作状态下的载荷特征数据，通过布置于起重机小车起升卷筒支撑位置的载荷传感器采集“起升载荷”，载荷传感器的读数由0再次变化为0记为一次工作循环，采集适当样本空间的载荷数据，以便获取的载荷特征参数样本(额定起升载荷、实际起升载荷、工作循环次数)能够真实反映该机器使用情况，按照此方法记录一段时间内的工作情况，统计整理现场实测数据，得到符合实际使用工况的小样本载荷谱。现场采集起重机载荷特征参数情况如图1所示。

1.2 起重机预测模型

本文以通用桥式起重机为研究对象，通过现场实测采集载荷特征参数数据，统计整理数据结果，获取真实反映该机器使用情况的小样本载荷谱，并将其分为训练集和测试集。此外，采用优化算法-改进的天牛须搜索算法对LSSVM预测模型进行参数的优化选择，输入训练集训练预测模型的性能，预测模型通过挖掘数据规律，形成输入和输出之间的映射关系，得到拟合性能较高的LSSVM预测模型，通过测试集回归拟合的结果，验证优化后的LSSVM预测模型具有较高的回归预测性能，可以为起重机载荷谱的样本扩展及疲劳剩余寿命研究奠定基础。起重机载荷谱回归预测的模型构建方式如图2所示。

图1 现场采集载荷特征参数Fig.1 Collect load characteristic parameters on site

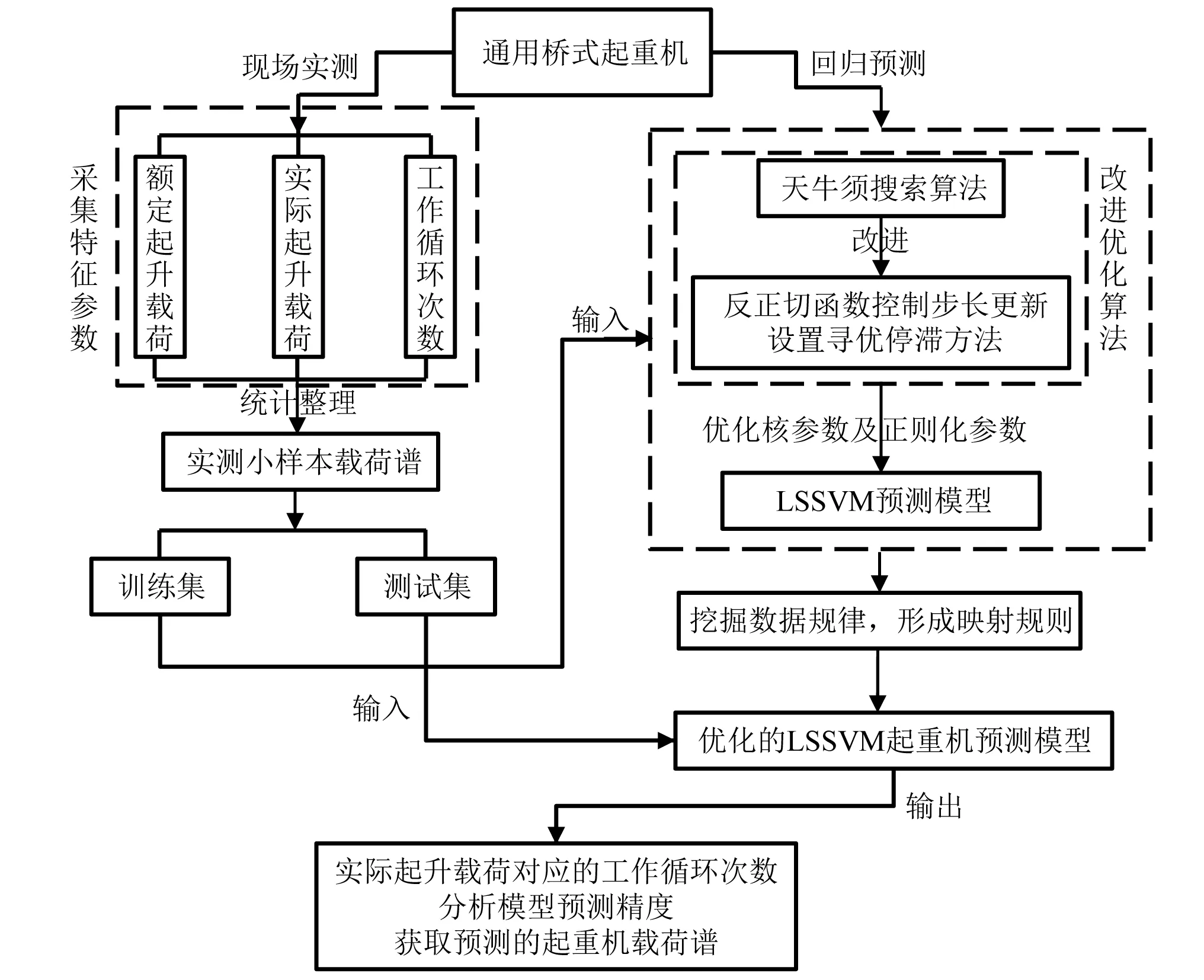
图2 起重机载荷谱回归预测模型Fig.2 Regression prediction model of crane load spectrum

2 最小二乘支持向量机

支持向量机由Vapnik等提出[29-30]，该方法基于结构风险最小化，可以解决机器学习中存在的过学习、维数灾难、非线性等问题，且泛化能力强，是一种用于数据分析的监督式机器学习模型，但其训练速度较慢，稳定性差是一个不可忽视的问题，20世纪90年代，Suykens等[31]在标准支持向量机的基础上提出最小二乘支持向量机算法，这是一种新型的回归预测算法，利用最小二乘法将原有支持向量机的二次规划优化问题中的非等式约束转换为求解线性方程组的等式约束，把误差平方和作为训练样本的损失函数，避免了复杂的二次规划问题，降低了样本点在训练过程中的复杂度，极大地提高了计算精度和预测速度，成为机器学习中的研究热点。

2.1 LSSVM基本原理

假设给定样本集A，如式所示

A={(xi,yi),xi∈Rn,yi∈R},i=1,2,…,m

(1)

式中：xi∈Rn为第i个维列向量的样本输入值；yi∈R为第i个输入值对应的一维输出值；m为样本的个数。

支持向量机的核心思想是通过寻找非线性映射函数φ(x)，将原空间的样本映射到高维特征空间，此时高维空间的样本集如式(2)所示

yi=ω·φ(xi)+b

(2)

式中：ω为权向量；ω·φ(xi)为向量x∈Rn与ω∈Rn的内积；b为偏置量。

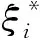
(3)

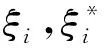
为解决SVM中的二次规划问题，LSSVM根据正则化理论和最小二乘函数，将式(3)中的不等式约束转化为等式约束，如式(4)所示

(4)

式中：γ为正则化参数；ei为误差向量。

图3 非线性支持向量回归机示意图Fig.3 Nonlinear support vector regression machine

构造拉格朗日函数求解式(4)的最优解，并得到式(5)

(5)

式中：∂i为拉格朗日乘子。根据最优化理论KKT(Karush-Kuhn-Tucker)条件，对式(5)的4个参数ω,b,∂i和ei求偏导数并令其等于零，如式(6)所示

(6)

对于i=1,2,…,m，通过式(6)消去ω和ei，得到如下线性方程组式(7)并求解

(7)

其中

(8)

令θ=DDT,引入满足Mercer条件的核函数K(xi,xi)=φ(xi)T·(xj)代替高维特征空间中的点积运算，简化模型的计算过程，此时可得式(9)

θ=yiyjφ(xi)Tφ(xj)=yiyjK(xi,xi)

(9)

将式(9)代入线性方程组式(7)中得到新的线性方程组式(10)

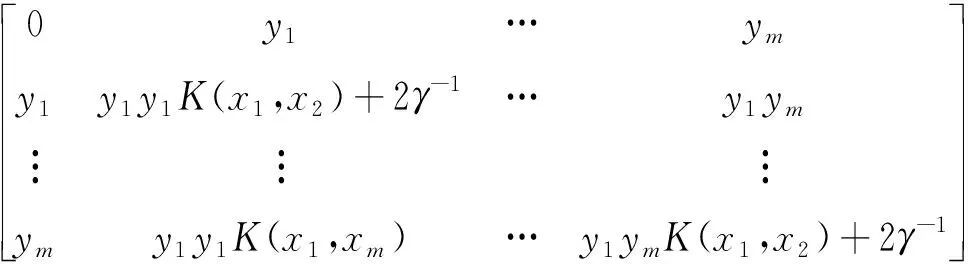
(10)

利用最小二乘法求解线性方程组式(10)，最终求得LSSVM模型的决策函数，如式(11)所示

(11)

2.2 核函数的选择

理论上，所有满足Mercer条件的函数都可以选择作为核函数，但是不同的核函数对于LSSVM的回归预测性能有着很大的影响，常见的核函数有:线性核函数、多项式核函数，高斯核函数和Sigmoid核函数。线性核函数是最简单的核函数，具体形式如式(12)；多项式核函数是非标准核函数，非常适合正交归一化数据，具体形式如式(13)；高斯核函数是一种经典的具有鲁棒性的径向基核函数，对数据中的噪声具有良好的抗干扰能力，具体形式如式(14)；Sigmoid核函数源自神经网络，现在广泛用于深度学习，它是S型的，常用作“激活函数”， 具体形式如式(15)。

(12)

(13)

(14)

(15)

最小二乘支持向量回归机的性能取决于许多方面，包括核函数的选择和支持向量回归机的参数。考虑到上述因素，首先要确定最小二乘支持向量回归机的核函数类型。根据经验和自己的试验，本文选择高斯核函数为预测模型的核函数，高斯核函数有着径向对称、光滑性好、收敛域宽和泛化能力强等优点。

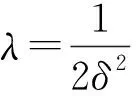
在基于高斯核函数的LSSVM预测模型中，标准化参数δ反映了训练样本数据分布特性，正则化参数γ决定了训练误差大小和泛化能力的强弱，是影响LSSVM预测性能的两个重要的超参数。在传统的LSSVM载荷预测中，这两个参数往往根据人工经验交叉验证和网格搜索的方法选取，为了提高选择超参数的速度和科学性，改善预测模型的性能，本文使用自主改进的天牛须搜索算法对最小二乘支持向量机预测模型中的超参数δ,γ的取值进行优化。

图4 核函数映射空间变换图Fig.4 Kernel function mapping space transformation

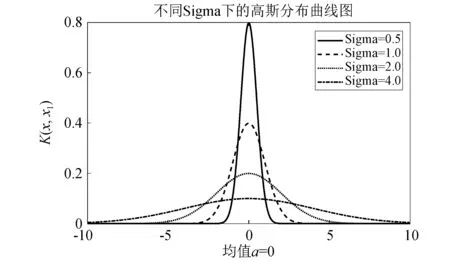
图5 高斯函数分布曲线图Fig.5 Gaussian function distribution curve

3 改进的天牛须搜索(IBAS)算法优化LSSVM模型

3.1 基本天牛须搜索(BAS)算法原理

天牛须搜索 (beetle antennae search，BAS)算法是由Jiang等[32]提出的一种新型仿生启发式智能优化算法，在目标函数具体形式和梯度信息未知的情况下，仅需要一个天牛个体便可实现全局寻优，算法简单，计算量小，在处理复杂优化问题上具有独特优势。BAS算法的灵感来自于天牛探测和寻找食物的行为，在食物位置未知的情况下，天牛通过左右两只触角探测并接收食物发出的味道信号强弱去判别前进方向。若左边触角收到的味道强于右边，天牛就向左前进，反之向右前进，如果左右触角收到的味道信号强弱相等，保持当前的前进方向不变，按照此规则寻找食物，直至成功觅食，觅食过程如图6所示。在觅食过程中，食物所在的位置，味道信号最强，天牛的目标就是寻找味道信号最强的点，算法的步骤如下。

步骤1设置算法的初始参数，两触角之间的距离l0；初始步长S,其取值与搜索区间范围大致相等；步长与触角之间距离的比值为z；迭代次数Dt和误差精度eps。

步骤2定义天牛初始质心位置为x，x为随机产生的一组k维向量，k由问题的性质决定。

步骤3计算左右两触角的位置，天牛头朝向为随机创建的方向向量b，将其单位化后，左右触角位置的计算方式如式(17)、式(18)

(16)

(17)

(18)

式中，xl,xr分别为每次迭代过程中的天牛左触角和右触角的位置。

步骤4以目标函数f(x)作为适应度函数，计算左右两触角位置的“食物味道信号”，更新下一个天牛质心位置，如式(19)

x=x+S×b×sign[f(xl)-f(xr)]

(19)

式中：sign(·)为符号函数，判断天牛下一步的前进方向；f(xl)和f(xr)分别为左触角和右触角对应的“食物味道信号”。

步骤5考虑到局部搜索能力，两触角的距离l0和步长S的更新计算公式如下

l0=v×l0+0.01

(20)

S=v×S

(21)

式中，v为变步长因子，取值范围为[0,1]，通常取0.95。

步骤6判断是否达到迭代停止准则，满足则停止，此时天牛质心位置即为全局最优解，否则返回步骤3继续运行直至满足要求。

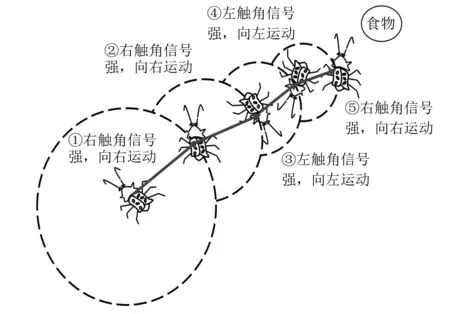
图6 天牛觅食过程Fig.6 Foraging process of beetle

3.2 IBAS算法

原始的BAS算法采用实数编码，计算过程简单且效率较高，迭代过程中的步长S为指数下降趋势，随迭代次数增加快速收敛到极值点，但仅让天牛搜索步长S指数下降减小，迭代后期步长会变得非常小，会使算法进入局部极值点邻域后很难继续寻找全局最优位置，为了解决这一问题，需要对原始天牛须搜索算法进行改进[33-34]，本文通过分析步长变化对算法的影响，采用反正切函数动态调整并更新步长S，调整方式如式(22)所示，从图7中可见，反正切函数比线性函数和指数函数有独特的优势，可以实现天牛个体在搜索初期保持较大的步长前进搜索，有利于扩大算法的查找范围，增强算法的全局优化能力，搜索中期步长快速下降，加快收敛速度，搜索后期步长减小的速度减缓，提高局部寻优能力，使算法更稳定。

h=arctan(20-q)+arctanq

(22)

式中：Sstart和Send分别为步长的初始值和终止值；t为当前的迭代次数；Tmax为最大的迭代次数；q为控制曲线衰减程度的调节系数。

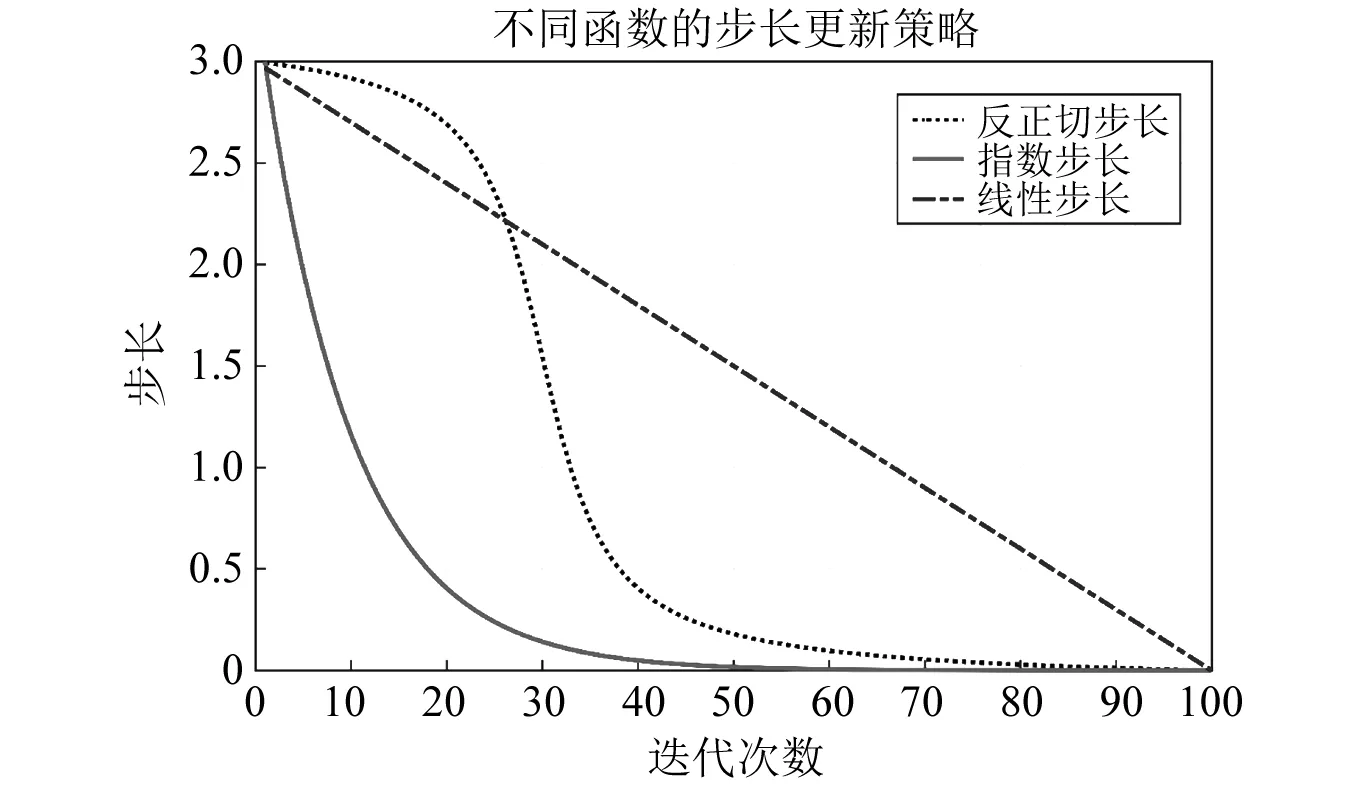
图7 不同步长更新策略的比较Fig.7 Comparison of different step update strategies

研究发现，仅仅使用反正切动态步长不能保证天牛具有良好的优化能力，当迭代到后期，天牛的步长和两触角之间的距离变的越来越小，不满足天牛此时探索更“广泛”的空间，导致天牛位置持续多代保持不变，停滞不前，容易使算法在后期陷入局部最优解迭代中。为了解决这个问题，本文设置如下方案，增强算法后期“相对广泛”的搜索能力，如图8所示。

图8中，设置迭代“停滞”次数K初始值为0, “停滞”是指当代天牛个体和和前一代天牛的个体适应度值f(·)的值相等时，此时，K值增加1，直到连续Bb次“停滞”，可能是适应度值不更新，算法陷入局部最优解。此时，令天牛个体搜索步长增大为St，St为跳出局部解的步长，适当地增强天牛的步长，提高局部优化能力并扩大了算法的寻优空间，有助于算法跳出局部最优解，此后，“停滞”次数K归0，天牛步长再次按照式(22)减小，继续进行判断算法“停滞”，直到满足迭代精度或最大迭代次数。

改进的天牛搜索算法(IBAS)分为两部分，第一部分：算法初期按照反正切函数特性更新步长，提高了算法的全局寻优能力和中期的快速收敛能力；第二部分：随着迭代次数的增加，为了防止算法陷入局部最优解，设置判断“停滞”和增大步长的功能，以跳出局部最优解。IBAS算法有效地提高了算法的整体优化能力。

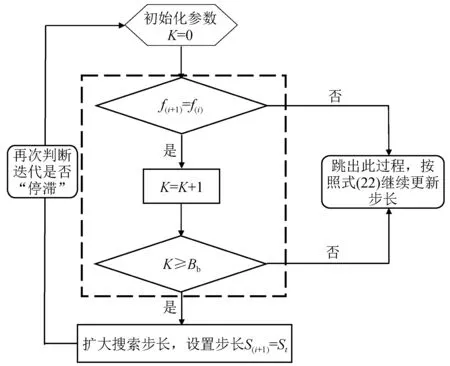
图8 判断“停滞”及步长更新图Fig.8 Judgment of stagnation and step update strategy

3.3 算法能力验证

为验证本文提出的改进的天牛须搜索算法的寻优能力，采用在智能优化算法评价中广泛使用的4个经典测试函数，4个测试函数的公式和函数的特性如表1所示。

根据表1可知，4个测试函数包括单峰函数和多峰函数，单峰值测试函数检测算法发掘群体信息的能力和收敛精度，多峰值测试函数检测算法勘探种群之外其他信息的能力和解决复杂优化问题的能力。4个测试函数在3维空间中的曲面如图9所示。

为验证本文改进算法的性能，分别选用经典粒子群算法(PSO)、原始天牛须搜索算法(BAS)和本文改进的天牛须搜索算法(IBAS)对以上4个测试函数进行计算分析。3种算法的初始参数设置如表2所示，分别在2维和10维设计空间下对3种算法进行计算分析，每种算法独立运行20次，设置迭代停止条件如式(23)所示，每一次迭代完成均记录迭代次数、计算时间和寻优适应度等结果。表3列出了3种算法运行20次的平均计算结果，表4列出了3种算法运行20次的平均迭代次数和计算时间，优化算法对4个测试函数寻优迭代曲线如图10～图13所示，横坐标用迭代次数表示，纵坐标用适应度对数值表示。

表1 测试函数

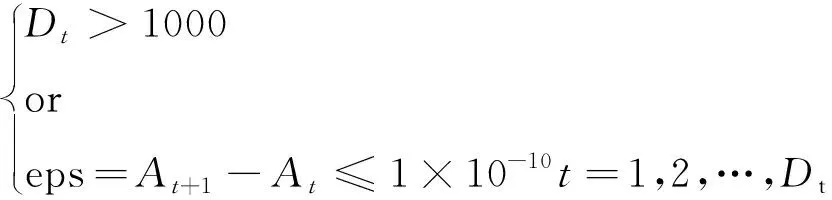
(23)

式中，Dt为迭代次数；eps为迭代精度；t为当前迭代次数；At+1为当代的适应度值；At为上一代的适应度值。

表2 3种算法初始参数设置

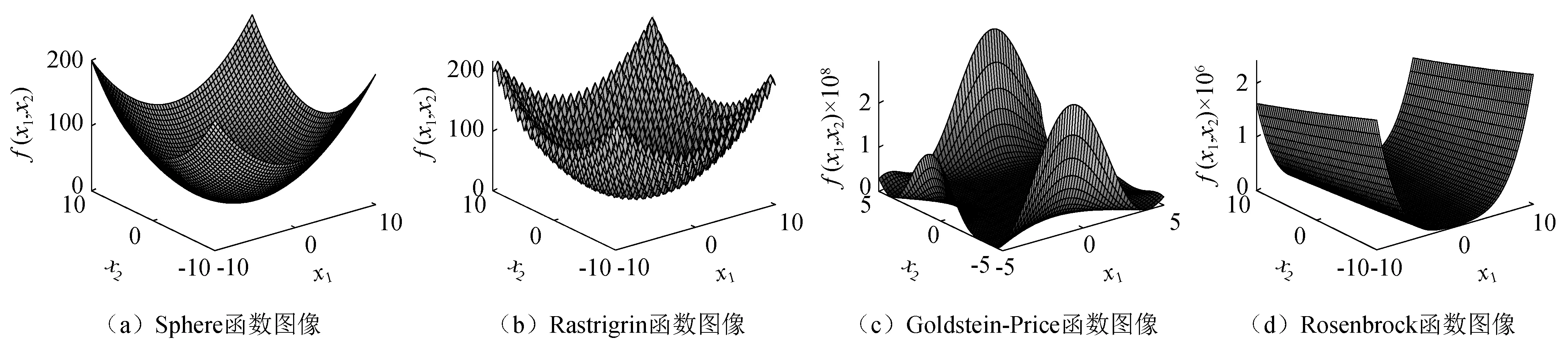
图9 4个测试函数的曲面图Fig.9 Surface figures of four test functions

表3 3种算法运行20次的平均计算结果

表4 3种算法运行20次的平均迭代次数和计算时间

表3和表4显示了3种优化算法对4个测试函数的寻优结果的性能对比，从表3可见，在对单峰值Sphere函数和多峰值Rastrigrin函数寻优时，在2维设计空间中，原始BAS算法的发掘能力较差，粒子群可以逼近到函数极值点0附近，但是本文提出的IBAS算法可以分别精确到1.13×10-10和1.79×10-10，在10维设计空间中，IBAS算法的计算结果同样明显地优于其他两种算法，说明其具有更好的寻优精度和避免陷入局部最优的能力；在对Rosenbrock函数寻优时，IBAS算法在2维和10维设计空间中，计算结果的精确度都比其他两个算法高出了两个数量级别以上，显示出它在解决复杂优化问题时的优异性能；在对天牛须搜索算法专用测试函数Goldstein-Price函数寻优时，可以发现，BAS和IBAS算法都可以搜索到函数的理论最优值，但是从表4可见，IBAS算法的计算效率比BAS算法提高了95%左右，在保持计算精度不变的条件下，IBAS具有更快的计算速度。为了更加直观地反映算法的收敛速度，图10～图13列出了3种算法对4种测试函数在特定设计空间维度下的收敛曲线对比图，可以看出，IBAS算法的收敛速度和计算精度都明显优于其他两种算法，尤其是对Sphere函数和多峰值Rastrigrin函数在2维设计空间寻优时，分别在迭代进行到250次和529次的时候，就满足迭代停止条件，达到了寻优精度的要求。

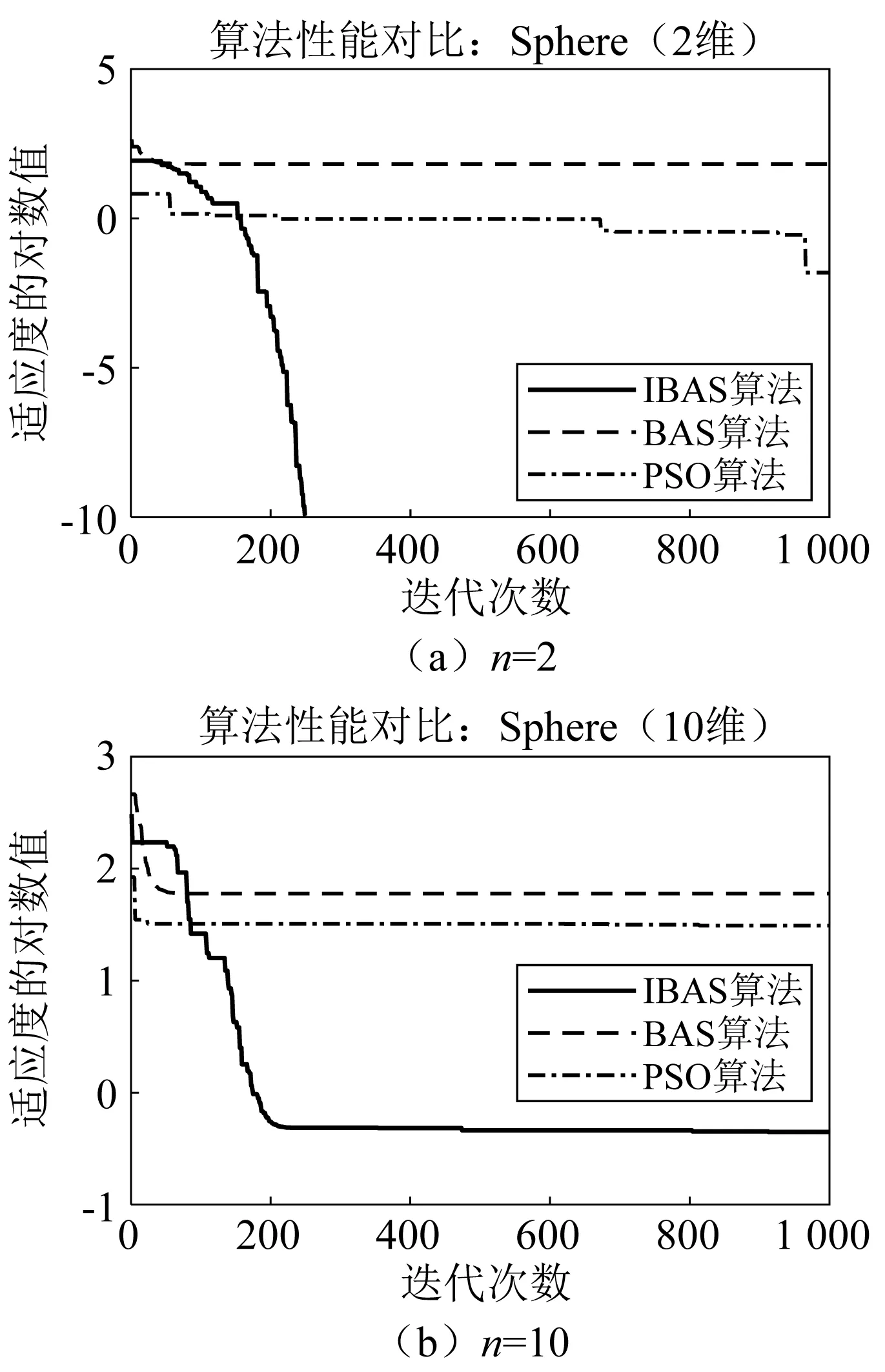
图10 测试函数1目标函数迭代曲线Fig.10 Objective function iteration curve of test function 1

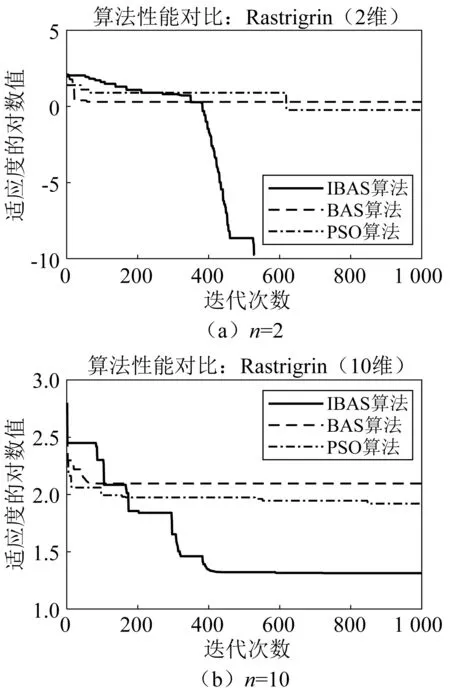
图11 测试函数2目标函数迭代曲线Fig.11 Objective function iteration curve of test function 2

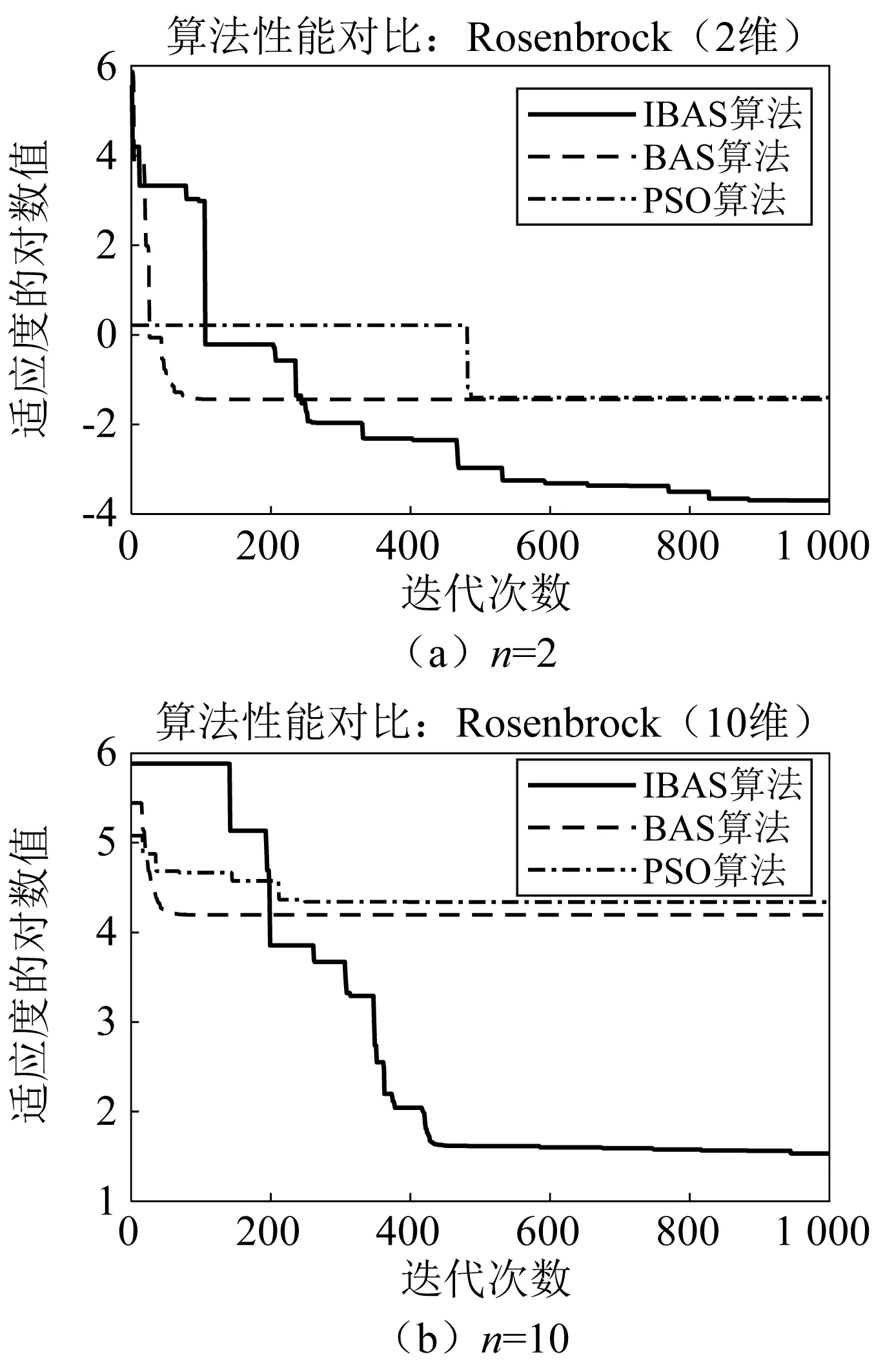
图12 测试函数3目标函数迭代曲线Fig.12 Objective function iteration curve of test function 3

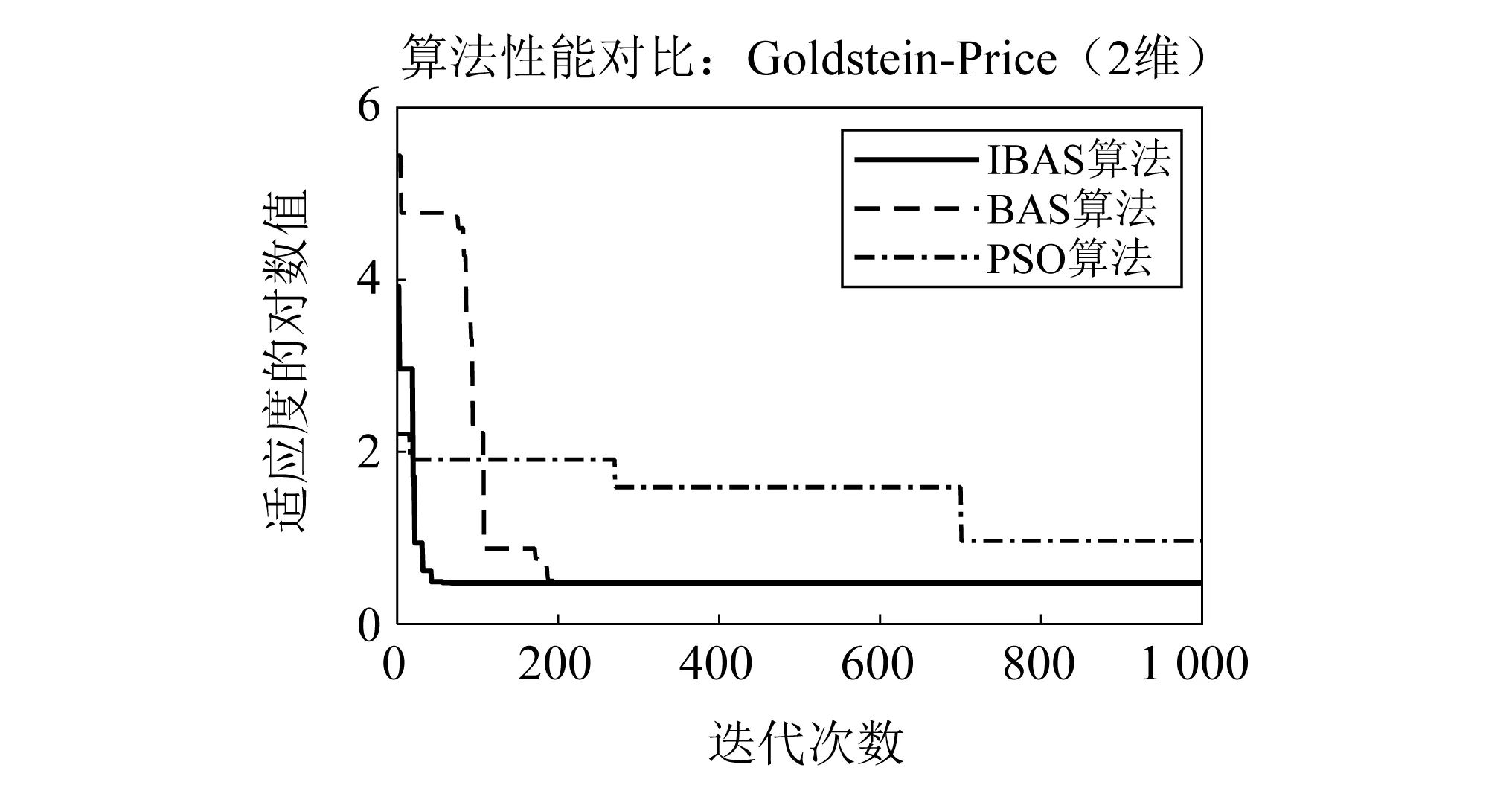
图13 测试函数4目标函数迭代曲线Fig.13 Objective function iteration curve of test function 4

综上所述，本文改进的天牛须搜索算法(IBAS)在相同条件下，不仅在低维空间具有优异的寻优性能，而且在高维空间也有较强的搜索能力，在解决复杂函数的优化问题时，具有计算精度高，计算速度快，探索能力强的优点，同时，跳出局优，克服早熟的能力也大大加强。

3.4 IBAS-LSSVM预测模型

本文利用最小二乘支持向量机(LSSVM)技术，研究起重机载荷谱的回归预测，由于LSSVM预测模型的性能取决于其LSSVM参数和核函数及其参数的选择，核函数选择高斯径向基核函数，此时，核函数参数δ和正则化参数γ的选择合适与否直接决定模型的预测精度和可靠性，因而采用改进的天牛须搜索算法(IBAS)优化模型中两个参数δ，γ，设置天牛质心初始位置x(x1,x2)，x1和x2分别对应于δ和γ。利用IBAS算法进行寻优迭代，找到满足精度要求的适应度函数值对应的最优解，实现对LSSVM参数的最优选择，再将寻优得到的最优参数代入LSSVM模型中进行训练，构造出最终的IBAS-LSSVM回归预测模型。

基于IBAS-LSSVM的起重机载荷谱回归预测流程如图12所示，主要步骤如下。

步骤1导入收集到的数据，将原始数据随机分成训练集和测试集，由于原始数据数量级不同，单位不同，为了综合对比分析，需要对数据作预处理，即数据的无量纲归一化，将原始数据映射到[0,1]内，线性归一化式(24)

(24)

式中：Y*为归一化后的数据；Y为原始数据；Ymax和Ymin为原始数据的最大值和最小值。

步骤2初始化IBAS算法的参数，设置两触角之间的距离l0，初始步长S等等，并随机生成天牛质心位置x(x1,x2)。

步骤3初始化LSSVM模型的参数，type=‘f’,kernel=‘RBF_kernel’,proprecess=‘proprecess’，定义LSSVM模型的分类器为回归预测，核函数为径向基核函数，导入的数据为归一化数据。

步骤4采用本文提出的IBAS算法优化核函数参数δ和正则化参数γ，计算初始天牛质心位置的适应度函数值，适应度评估函数采用预测值的均方根误差，如式(25)

(25)

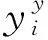
步骤5按照式(17)和式(18)计算天牛左右触角的位置坐标xl和xr，由适应度函数式(25)计算天牛左右触角的适应度函数值F(xl)和F(xr)。

步骤6按照式(19)计算出天牛质心的新位置xn+1并计算其适应度函数值F(xn+1)。

步骤7随着迭代次数的增加，判断天牛质心位置的适应度函数值是否“停滞”及步长更新与否，如图8所示。

步骤8判断适应度函数值是否满足误差要求或者达到最大迭代次数，若是，转到步骤9，否则转回步骤5继续迭代。

步骤9此时天牛质心位置x(x1,x2)为最优参数选择，按照x1和x2对应的δ和γ作为最佳参数，代入LSSVM预测模型，并输入测试集进行载荷预测。

步骤10根据测试集的输出值和实际值，计算归一化均方根相对误差，平均绝对误差，拟合度，对比分析验证模型的准确性。

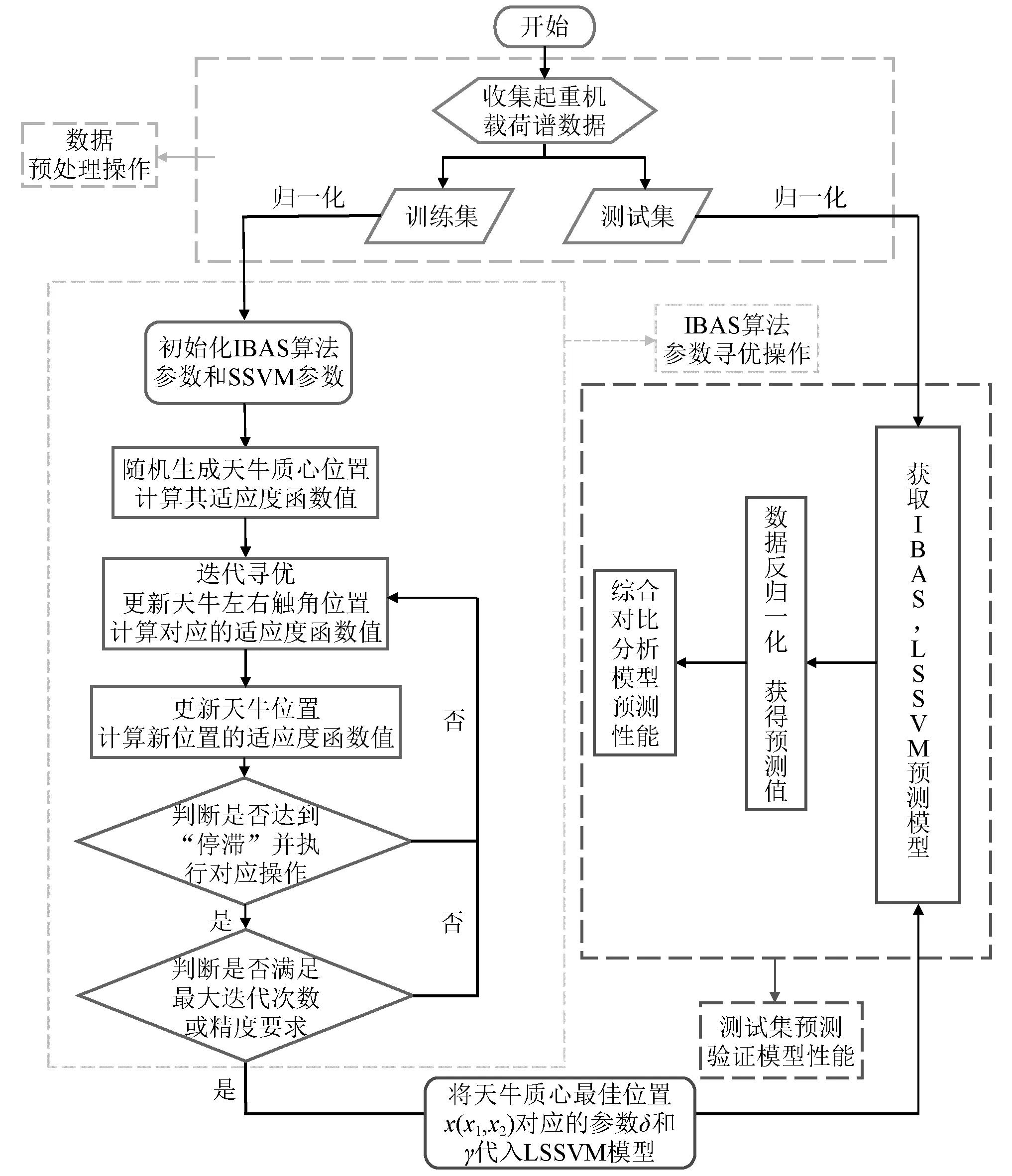
图14 IBAS-LSSVM的起重机载荷谱回归预测流程图Fig.14 IBAS-LSSVM crane load spectrum regression prediction flowchart

4 工程实例

4.1 数据获取和模型搭建

本文以某型号通用桥式起重机结构载荷谱预测为例，该起重机的额定起质量为32 t，跨度为28.5 m，整机工作级别为A5，按照1.1节中介绍的方法，采集起重机实际工作状态下30天的60组载荷-时间历程数据，如表5所示，得到载荷谱特征参数，即额定起质量，实际起升载荷，工作循环次数。为了验证IBAS-LSSVM预测模型对于起重机载荷谱预测结果具有更好的性能，将数据分为训练集和测试集，额定起质量，实际起升载荷作为输入变量，工作循环次数作为输出变量，随机选取50组数据进行训练，剩余10组数据进行测试，分别采用RF(random forest)，SVM，LSSVM，BAS-LSSVM，IBAS-SVM 5种模型进行起重机载荷谱预测试验，初始参数设置见表6。

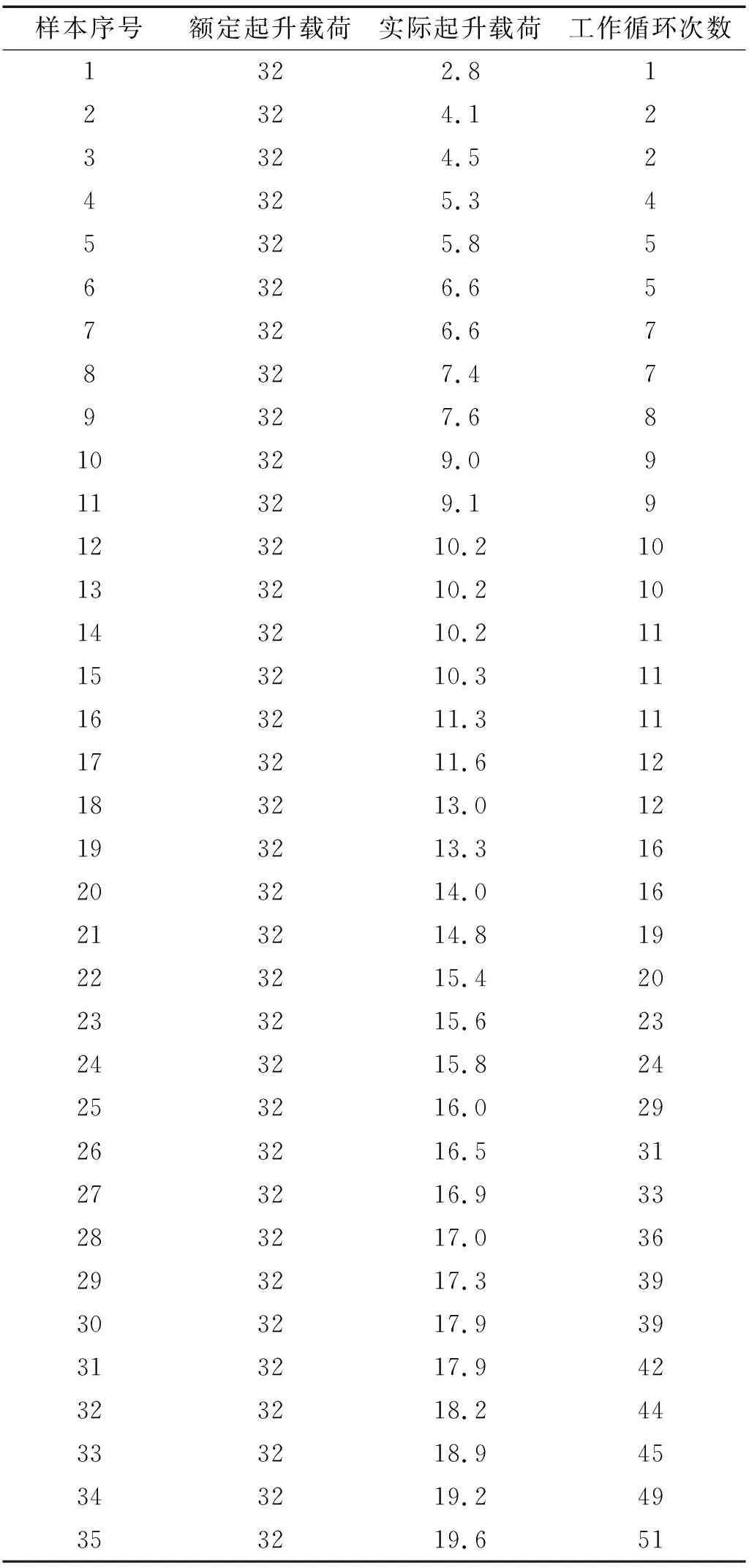
表5 载荷-时间历程数据

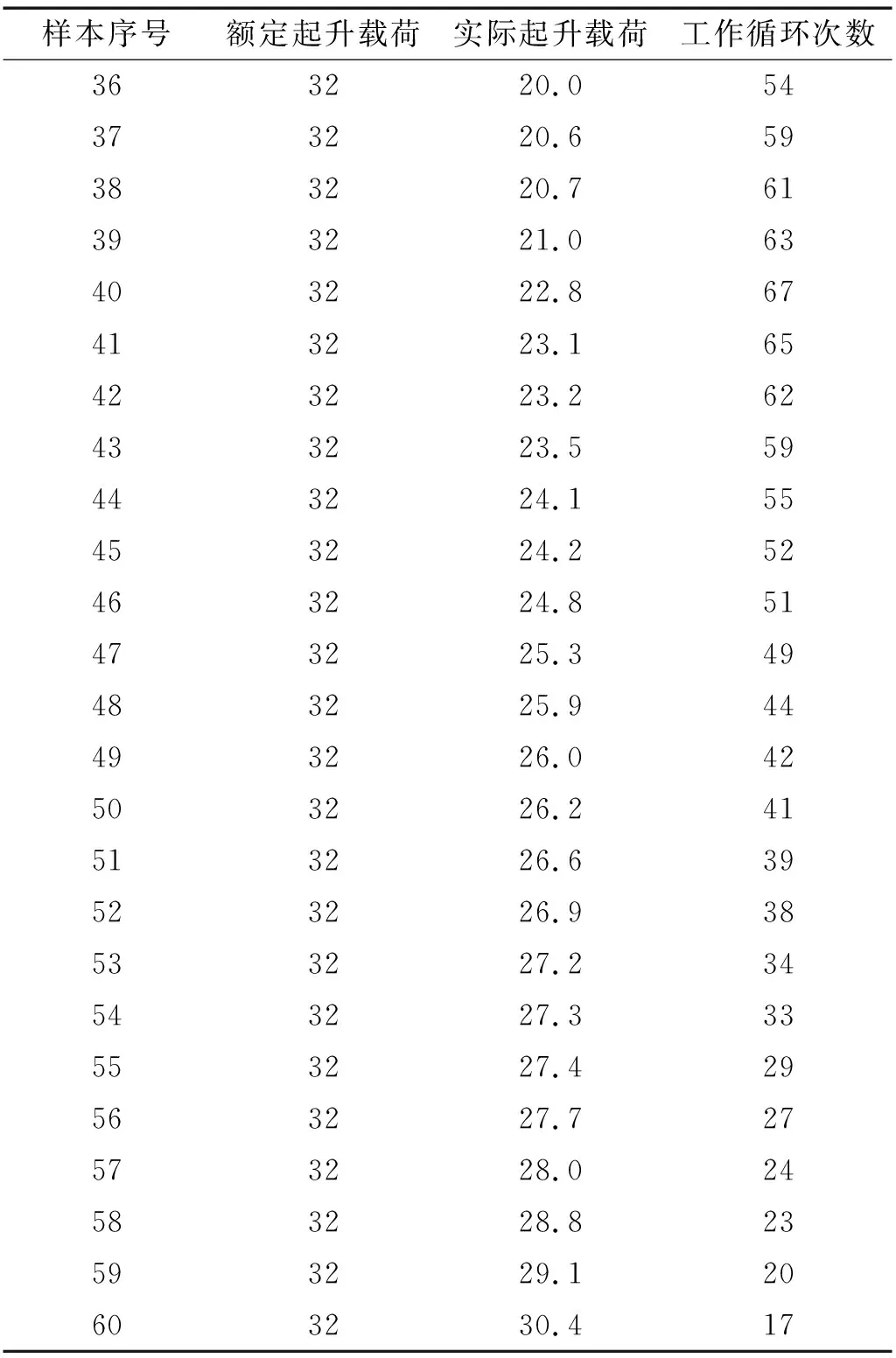
续表5

表6 不同起重机载荷谱预测模型初始参数设置

4.2 验证IBAS-LSSVM预测模型

基于4.1节的试验前期准备，每个预测模型在对测试集进行预测之前，先对训练集进行学习，试验表明，计算机运行次数越多，模型的稳定性越好，在MATLAB独立运行10次后，预测结果保持基本不变，模型基本达到稳定状态，再对测试集进行回归拟合，得到每个模型的起重机载荷谱预测结果以及IBAS算法获取的核参数，见表7，根据试验数据，基于MATLAB绘制工作循环次数实际值和各个模型预测值的对比折线图，如图13、图14所示，其相对误差图如图15所示。

从图13和图14可以看出，6种模型的预测结果都与真实值具有相同的变化趋势，图14中模型的预测效果明显优于图13，图13中的RF模型在前4个样本点的预测值偏差较大，SVM模型在后5个样本点的预测值偏差较大，LSSVM模型的预测曲线与真实值基本吻合；经过天牛须搜索算法及其改进后的算法优化以后，图14中的3个模型预测的性能明显提高，BAS-LSSVM模型在第一个点的预测结果较差，而IBAS-LSSVM模型的预测曲线相对最逼近真实值，预测性能最优。

从图15中，可以明显看出各个模型在10个测试点的相对误差值大小，RF，SVM，LSSVM模型的最大相对误差分别为0.15，0.1，0.4；BAS-LSSVM，IBAS-SVM，IBAS-LSSVM模型的最大误差分别为0.18，0.1，0.08，经过改进的天牛旭优化的LSSVM模型相对误差最小。

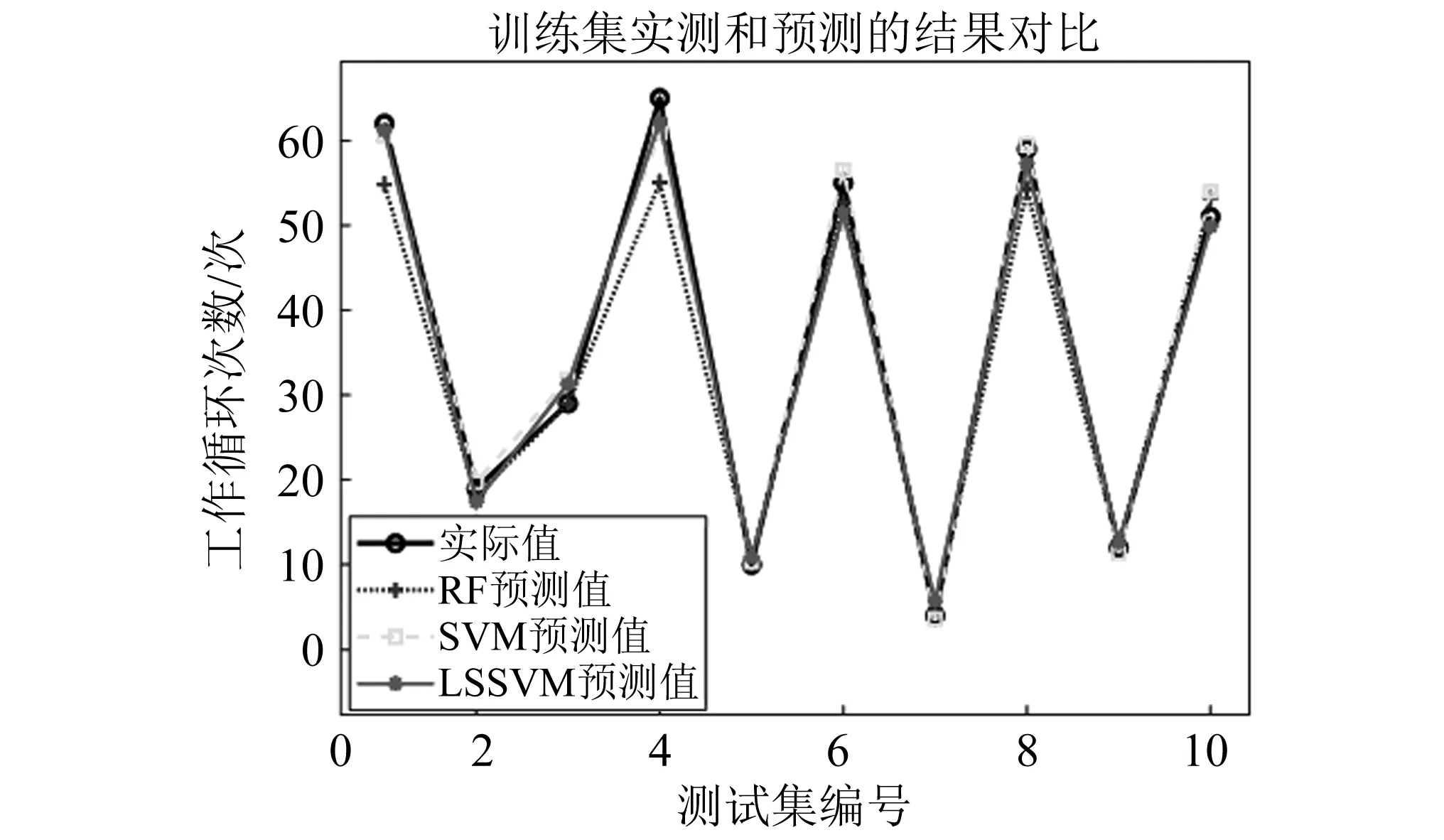
图15 RF,SVM,LSSVM预测结果Fig.15 RF,SVM,LSSVM prediction results

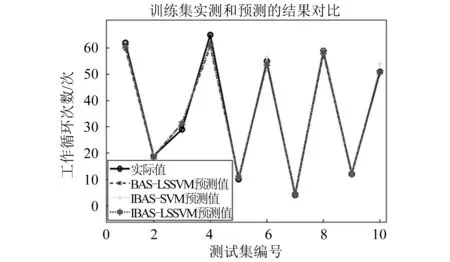
图16 BAS-LSSVM,IBAS-SVM,IBAS-LSSVM预测Fig.16 BAS-LSSVM,IBAS-SVM,IBAS-LSSVM prediction results

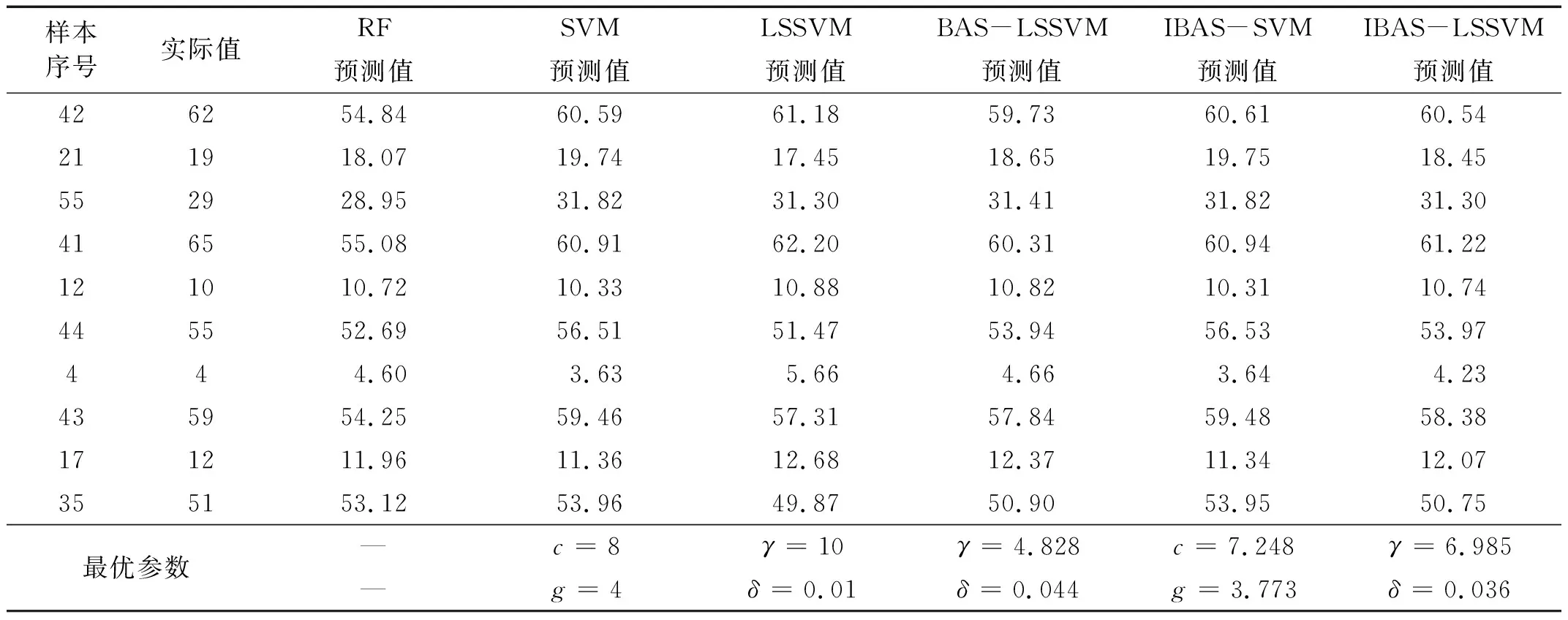
表7 不同预测模型对测试集的预测结果及训练的最优参数

图17 6种起重机载荷谱预测模型相对误差Fig.17 Relative errors of six crane load spectrum prediction models

为了更合理客观地直接评价各个模型的预测精度和所需的计算时间，本文采用均方根误差(root mean squared error,RMSE)、平均绝对百分比误差(mean absolute percentage error,MAPE)和拟合度(R2)作为评价标准，具体如式(26)～式(28)所示，并记录迭代运行时间，由于机器学习方法预测结果具有不稳定行，为提高模型的可靠性，需要多次试验记录数据，所以采用每个模型独立运行20次，计算数据的平均值，不同模型的预测性能对比数据如表8所示。BAS-LSSVM，IBAS-LSSVM预测模型通过训练集搜索最优参数的适应度迭代图如图18所示。

(26)

(27)

(28)

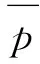
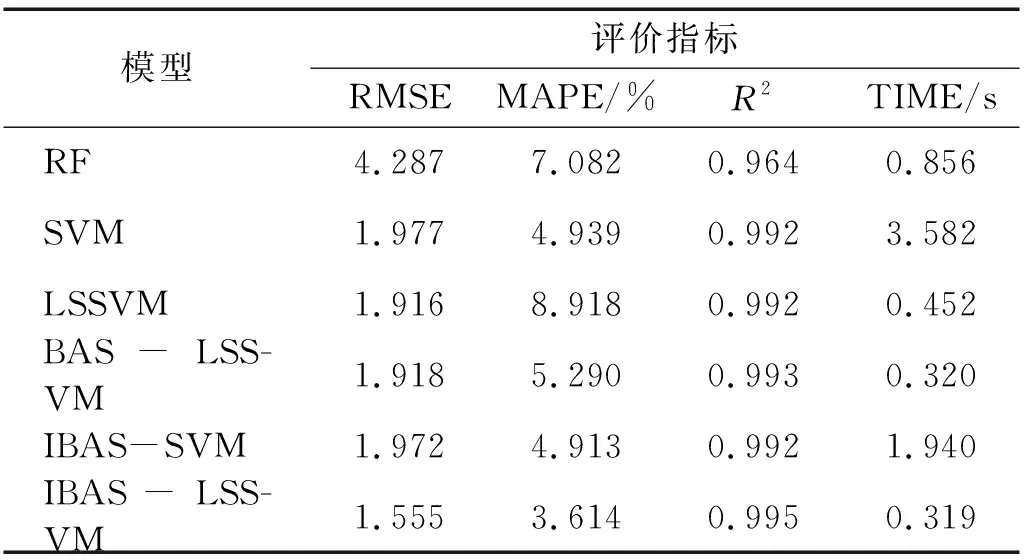
表8 不同预测模型测试性能对比

从表8可以看出，IBAS-LSSVM模型的RMSE值相比于LSSVM和BASSVM模型减少了0.361左右，更是比RF模型减小了2.732，IBAS-LSSVM模型的MAPE值和拟合度分别达到3.614%和0.995，都是6个模型中最优的，此外，可以发现，LSSVM及其优化后的模型的计算速度明显优于RF和SVM模型，验证了最小二乘支持向量机计算速度快的优点，从图18可见，IBAS-LSSVM模型在第10次就已经收敛，而BAS-LSSVM模型在大约第60次迭代才收敛，充分证明所提出的改进天牛搜索算法步长更新方式的合理性，可以快速有效的通过训练集样本选择出最优的核参数，大大提高收敛速度和预测精度，综上所述，IBAS-LSSVM模型的综合性能最优，可以实现对起重机载荷谱的精确预测。

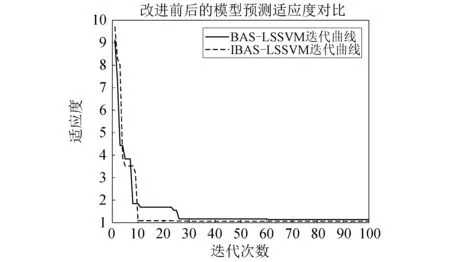
图18 BAS-LSSVM,IBAS-LSSVM模型预测适应度迭代曲线图Fig.18 Iteration curve of fitness predicted by BAS-LSSVM and IBAS-LSSVM models

5 结 论

(1)最小二乘支持向量机对小样本回归具有很强的逼近能力，被用于非线性拟合回归预测的建模，以此为基础，将现场实测数据中的额定起升载荷、实际起升载荷作为输入变量，工作循环次数作为输出变量，建立IBAS-LSSVM起重机载荷谱预测模型，使用人工智能方法来识别和训练输入和输出之间的非线性和复杂关系，从而达到预测的目的。

(2)天牛搜索算法(BAS)作为一种新型的智能算法，结构简单，计算速度快，易于操作，但容易出现早熟和局部最优的现象。本文改进的天牛须搜索(IBAS)算法中，步长采用反正切函数更新，并增设判断“停滞”环节，为了验证算法性能，通过计算测试函数，与其他算法做比较，发现IBAS算法可以很好地处理单、多峰值优化问题，在保证原有收敛速度和计算速度的前提下，能够克服原始天牛须搜索算法在寻优后期容易陷入局部极值的问题，尤其是在低维设计空间，优化效果极其明显，极大地提升了全局寻优能力。

(3)利用IBAS算法优化LSSVM模型中的核函数参数δ和正则化参数γ的选取，将IBAS-LSSVM预测模型应用于工程实例——起重机载荷谱回归预测中，通过与其他优化和预测方法(随机森林、支持向量机等)的比较，从详细的试验结果可见，IBAS-LSSVM模型可以实现对现场实测的60组载荷谱数据准确地回归预测,预测精度高、收敛速度快，是一种可行的快速起重机载荷谱预测方法。