车辆刚度阻尼多级可调式油气悬架系统分析及控制研究

汪少华， 翟旭辉， 孙晓强， 施德华， 殷春芳

(江苏大学 汽车工程研究院，江苏 镇江 212013)

油气悬架是一种以液压油作为承载介质，以氮气作为弹性介质的悬架系统，其具有承载质量大、刚度阻尼特性非线性变化等优点，广泛应用于工程机械以及军用车辆上[1-2]。由于应用油气悬架的车辆多行驶在恶劣工况条件下，传统的被动油气悬架系统难以保证车辆的操纵性能以及乘坐人员的舒适性，越来越多的学者开始研究刚度阻尼可调式油气悬架系统[3]。目前，对油气悬架阻尼可调的研究主要包括改变液压阀口的过流面积和控制可控流体黏度两大类，对油气悬架刚度可调的研究方法大多采用通过控制附加蓄能器的参数实现刚度可调。相关研究表明，上述方法能够提高油气悬架系统的性能，但是实现控制的难度较大，且结构复杂、成本较高。因此，进一步研究结构可靠、低能耗且控制简单的刚度阻尼多级可调式油气悬架系统具有重要意义[4-5]。

关于刚度阻尼多级可调式油气悬架，已有学者进行了研究。杨杰等[6]设计了一种刚度阻尼多级可调式油气悬架，当油气悬架的工作压力达到阀值时，刚度模式进行切换，建立了其非线性刚度阻尼数学模型，并通过台架试验进行模型验证。Sun等[7]通过调整高速开关阀的状态，改变了减振器的阻尼模式，通过建立具有连续和离散系统输入的混合逻辑动态模型，解决了系统最优控制问题。李仲兴等[8]对两级压力式油气悬架系统刚度特性进行了仿真，通过增加附加气室的方法实现系统刚度可调，结合MATLAB/Simulink分析了在随机路面输入下油气悬架系统对车辆平顺性的提升效果。

总体看来，目前对于刚度阻尼可调式油气悬架系统的研究多集中于单方面的刚度可调或阻尼可调，缺少对刚度和阻尼整体可调的油气悬架系统及其控制方法的研究。同时现有可控悬架系统刚度阻尼调节过程中普遍存在模型构建难、精度要求高且能耗偏大等问题。据此，本文提出一种基于高速开关电磁阀的刚度阻尼多级可调式油气悬架系统结构，通过分析其工作原理，建立其刚度阻尼特性数学模型，进而根据车辆悬架设计要求，确定了新型油气悬架系统的关键部件参数，随后进行模型仿真与试验验证。在此基础上利用粒子群优化算法(particle swarm optimization, PSO)对不同行驶工况下油气悬架系统刚度阻尼特性进行了优化匹配，设计了模式切换控制方法，最后对系统控制性能进行了验证。

1 新型油气悬架系统结构设计与数学建模

1.1 油气悬架系统结构设计

所设计的刚度和阻尼多级可调式油气悬架系统由液压油缸、阻尼阀系、蓄能器、开关电磁阀等组成。如图1所示，阻尼阀系连接液压油缸无杆腔1与液压油缸有杆腔2，包括单向阀3、节流阀4，5，6和开关电磁阀7，8，其中节流阀的节流孔直径不同，通过控制开关电磁阀7，8的开、闭能够实现油气悬架阻尼四级调节；蓄能器A，B并联，且两个蓄能器初始充气压力不同。通过控制开关电磁阀9，10的开闭能够实现油气悬架刚度两级调节。

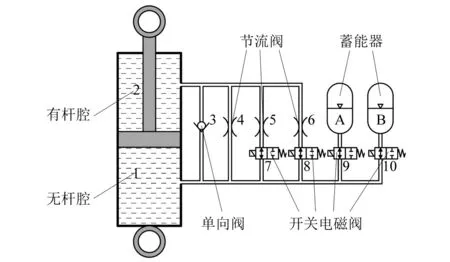
图1 油气悬架结构原理图Fig.1 Structural schematic diagram of HPS

在油气悬架工作过程中，通过控制内置高速开关电磁阀的状态能够实现8种输出力模式，实现方式如表1所示。

表1 输出力模式

以表1中模式1(软刚度、小阻尼)和模式8(硬刚度、大阻尼)为例，分析油气悬架的油液流向分别如图2和图3所示。

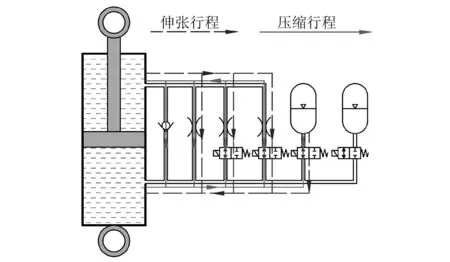
图2 小阻尼、软刚度模式的工作原理Fig.2 Working principle of small damping and soft stiffness mode

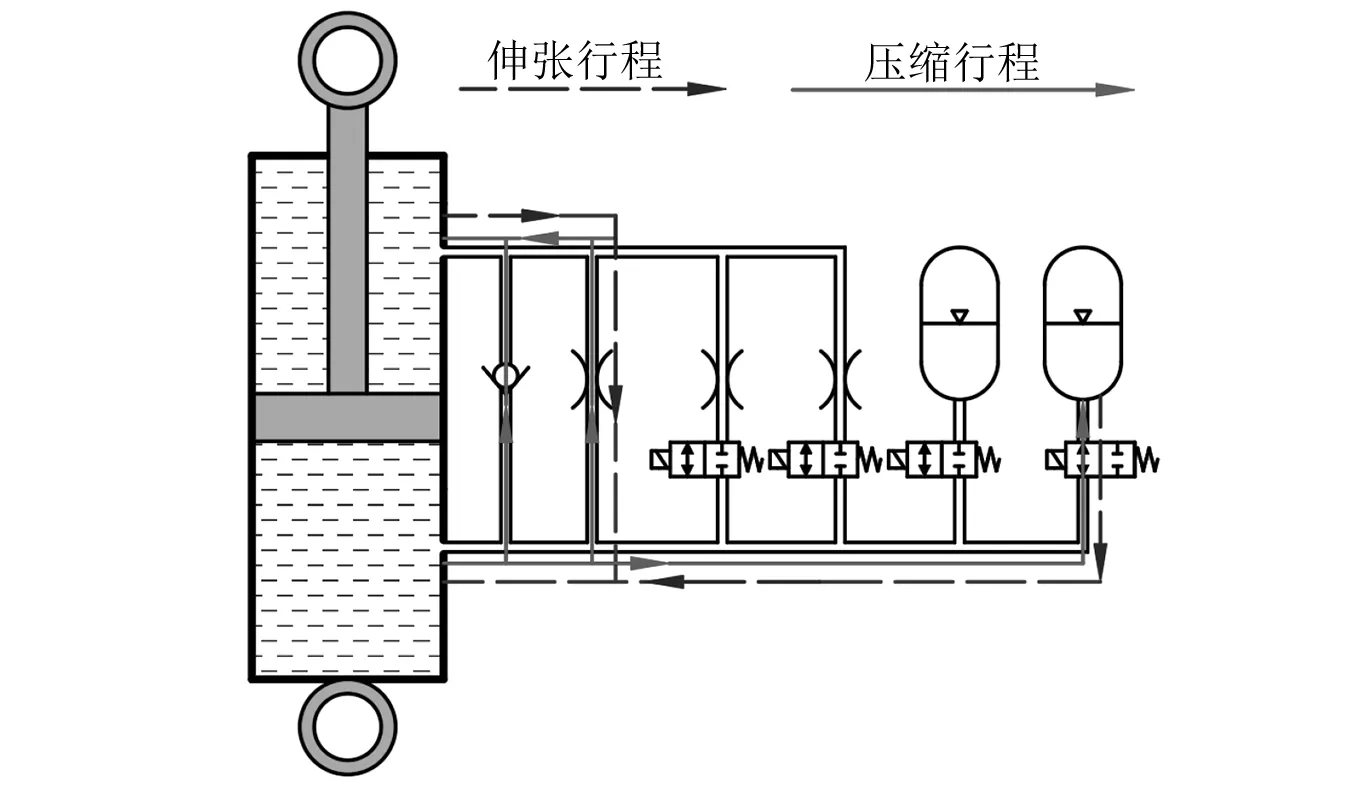
图3 大阻尼、硬刚度模式的工作原理Fig.3 Working principle of high damping and hard stiffness mode

1.2 油气悬架系统数学模型建立

根据油气悬架液压缸的工作原理，假设油气悬架满载时静平衡时的位置为原点，以活塞和缸筒相对运动的位移为坐标轴，活塞相对于液压缸向下运动时，规定其位移和速度方向为正，对活塞进行受力分析，活塞作用力包括由液压缸腔1和腔2之间压力差所产生的作用力和活塞和液压缸配合表面之间的摩擦力

(1)

式中：P1，P2分别为无杆腔1和有杆腔2的压力；S1，S2分别为无杆腔1和有杆腔2的有效液压面积，Fd为动摩擦力。

油气悬架的弹性力主要来于蓄能器，用理想气体状态方程来描述蓄能器内气体的状态变化过程[9]。

(2)

式中：P0，P为初始气体压力和瞬时气体压力；V0，V为初始气体体积、瞬时气体体积；r为气体多变指数。

当开关电磁阀9打开，10关闭时，油气弹簧处于软刚度模式，软刚度下的弹性力与刚度计算如下

(3)

(4)

当开关电磁阀9关闭、10打开时，油气弹簧处于硬刚度模式，其弹性力与刚度计算如下

(5)

(6)

油气弹簧阻尼力的来源主要有以下几个方面[10]：第一部分是油液流经阻尼阀系所产生的阻尼力，这部分产生的阻尼力是油气弹簧阻尼力的主要来源；第二部分是油液在管道流动过程中的管路沿程压力损失和油液进口局部压力损失所产生的阻尼力；第三部分是活塞在液压缸内运动的摩擦产生的阻尼力。

阻尼阀系的4种阻尼力模式数学模型计算如下

(7)

式中：Az4为节流阀4的过流面积；Ad为单向阀的过流面积；Cd为流量系数；ρ为油液密度；Az5为阻尼孔5的过流面积；Az6为阻尼孔6的过流面积。

则阻尼阀系的4种阻尼系数计算如下

(8)

管路沿程压力损失部分的阻尼力

(9)

式中：λ为沿程阻力系数；L为油管长度；dq为油管直径。

管路沿程压力损失部分的阻尼系数为

(10)

管路局部压力损失部分的阻尼力

(11)

式中，Aa为油管端口的过流面积。

管路局部压力损失部分的阻尼系数为

(12)

活塞与缸筒摩擦产生的阻尼力

(13)

式中：Fs为静摩擦力；xt为达到动摩擦时的速度。

活塞与缸筒摩擦产生的阻尼系数为

(14)

经过以上推导可以得到油气悬架的4种阻尼力数学模型为

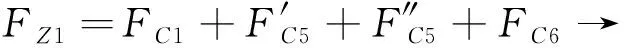
(15)

油气悬架的4种阻尼系数数学模型如下

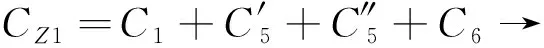
(16)

2 油气悬架系统模型仿真与试验对比

2.1 油气悬架系统主要结构参数确定

2.1.1 刚度范围的确定

车身自然振动频率由油气悬架系统刚度及簧载质量共同决定，是油气悬架结构参数以及参数变化范围设计计算的重要依据，其计算公式如下[11]

(17)

式中：f0为自然振动频率，取1.3～1.8 Hz；m2为簧载质量，m2=1 750 kg。

通过计算可得悬架刚度范围k=116～224 kN/m。

根据相关文献[12]，蓄能器初始充气压力的计算公式为

(15)

式中：S为蓄能器截面积；Δx为蓄能器内油液高度差。

2.1.2 阻尼范围的确定

根据汽车设计的相关理论[13]，在油气弹簧振动时，用相对阻尼系数评定振动衰减的快慢程度。表达式为

(16)

式中，ξ为相对阻尼系数，取0.19～0.39。通过计算可得悬架阻尼系数的范围c=5.4～15.0 kN·s/m。

根据油气悬架阻尼系数的范围可计算出节流孔直径，一般要进行大量重复的试验来确定节流孔直径[14]。试验步骤如下：

步骤1首先选择某一节流孔直径；

步骤2设计相同频率不同振幅的激励信号，试验得到油气悬架的示功图，求出其各个最大速度点v1，v2，…，vn及其各个速度点对应的阻尼力f1，f2，…，fn；

步骤3利用最小二乘法计算线性阻尼系数；

实际上阻尼力与速度成非线性关系，为方便计算可把阻尼力与速度视为正比的线性关系，即f=Cv。假设试验中测得的n个数据为(f1，v1)，(f2，v2)，…，(fn，vn)，线性阻尼系数为Cr，则可推算出试验数据误差的平方和表达式，如下所示

Δ=(Crv1-p1)2+(Crv2-p2)2+…+(Crvn-pn)2

(20)

取Δ=Δmin，则有

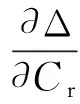
(21)

线性阻尼系数Cr计算如下

(22)

步骤4对比线性阻尼系数与设计值。

将阻尼系数的设计值与线性阻尼系数进行对比，如果两者相等，说明所选取的节流孔直径满足试验要求，反之，重复以上步骤直到得到正确的节流孔直径。

2.1.3 油气悬架工程化设计

当油气悬架处于静平衡位置时，液压缸的最大静态输出力F由工作压力P和活塞的截面积A所共同决定，如下所示

(22)

式中：D为液压缸直径；G为1/4车辆满载时的重力。

经过计算后可以得到液压缸的直径D为119.6 mm，取整到120 mm。油液密度、流量系数等参数依据选用标准按经验获得[15]。油气悬架关键结构的参数如表2所示。

表2 油气悬架参数

确定油气悬架的关键参数后，对其外部油路进行设计。各阀插装在阀块上，阀块的油路设计如图4所示。

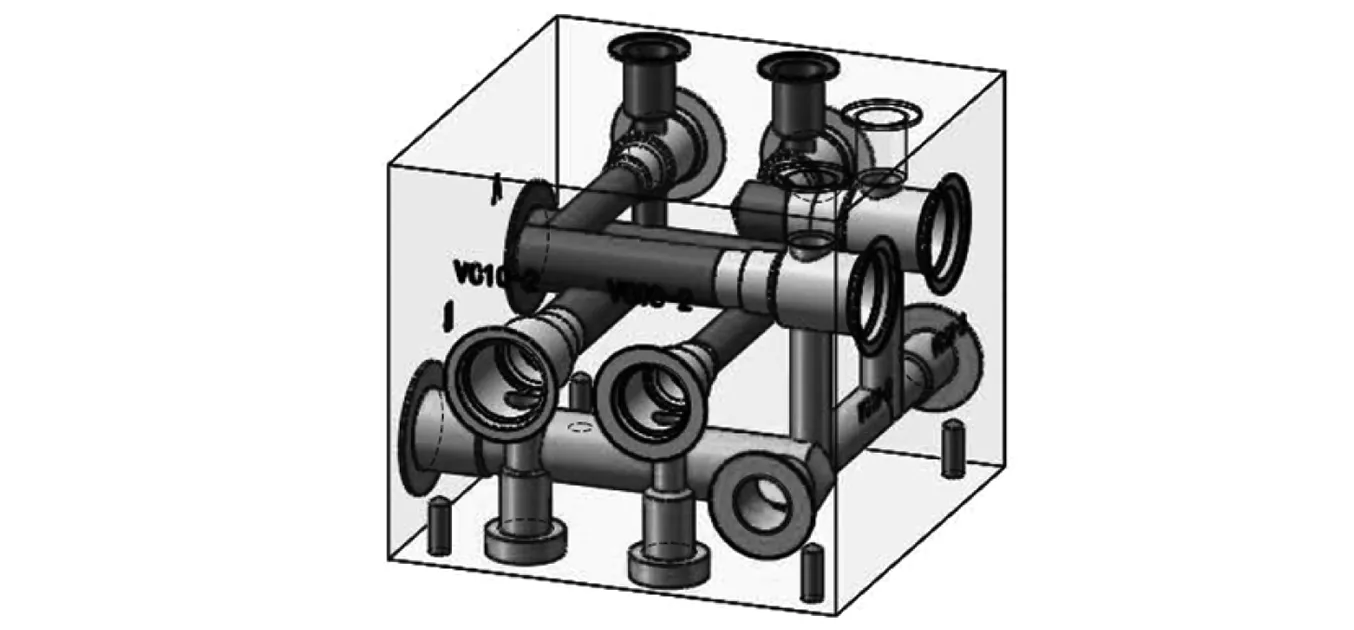
图4 阀块的油路设计 Fig.4 Oil circuit design of valve block

2.2 油气悬架系统试验对比

根据油气悬架系统各部件具体参数，加工并搭建油气悬架实物样机如图5所示。

图5 油气悬架试验样机Fig.5 Hydro pneumatic suspension test prototype

本文采用高速开关电磁阀型号为HSV-3103S7，额定流量4 L/min，频响50 Hz。油气悬架与台架试验台的安装方式为吊耳连接，通过辅助吊耳和连接板，将油气悬架试验样机固定在试验台架上，如图6所示。

图6 油气悬架台架试验台Fig.6 Hydro pneumatic suspension test bench

油气弹簧静态特性试验指的是当蓄能器处在一定的充气压力时，给油气弹簧特定激励使其缓慢作动，得到关于位移和弹性输出力的关系曲线的试验。图7为油气弹簧的静态特性试验与仿真试验曲线对比。与仿真曲线相比，试验曲线的弹性输出力要略大一点，分析其原因主要是因为试验过程中油液的缓慢流动使阻尼阀产生一定的阻尼力。

油气弹簧动态特性试验是指在一定的激励信号下，得到油气弹簧的速度特性曲线和位移特性曲线，即输出力和活塞相对速度之间的关系曲线和油气弹簧输出力和活塞相对位移之间的关系曲线。本次试验的输入为频率1 Hz、振幅为40 mm的正弦激励信号，以油气悬架输出力模式1、模式4和模式8为例进行分析，结果如图8～图10所示。

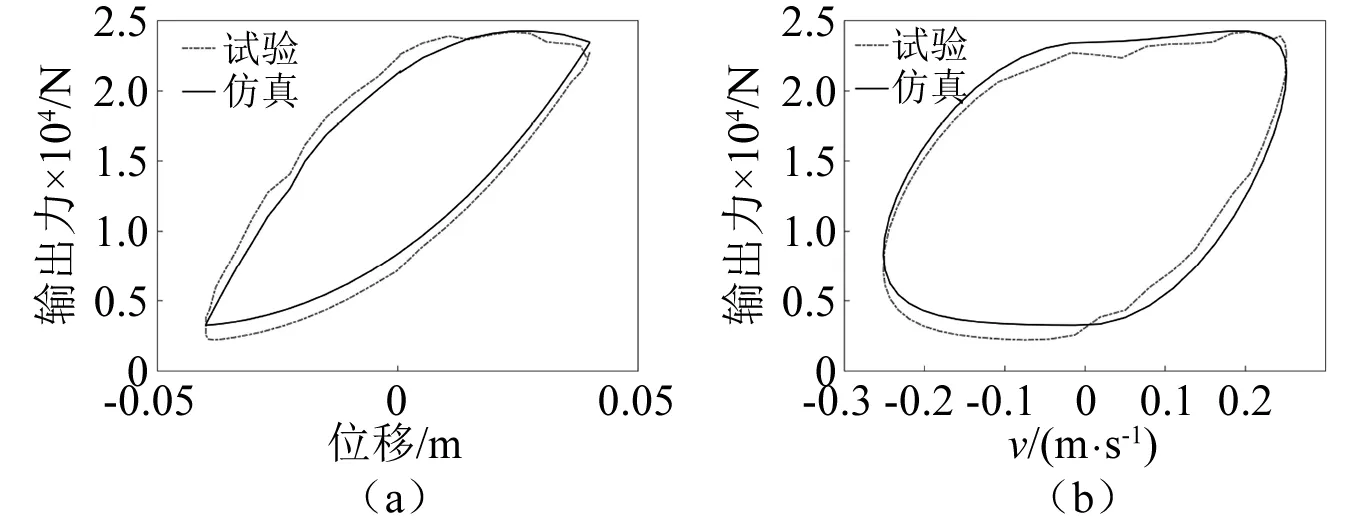
图8 输出力模式1试验与仿真对比图Fig.8 Comparison diagram of output force mode 1 test and simulation

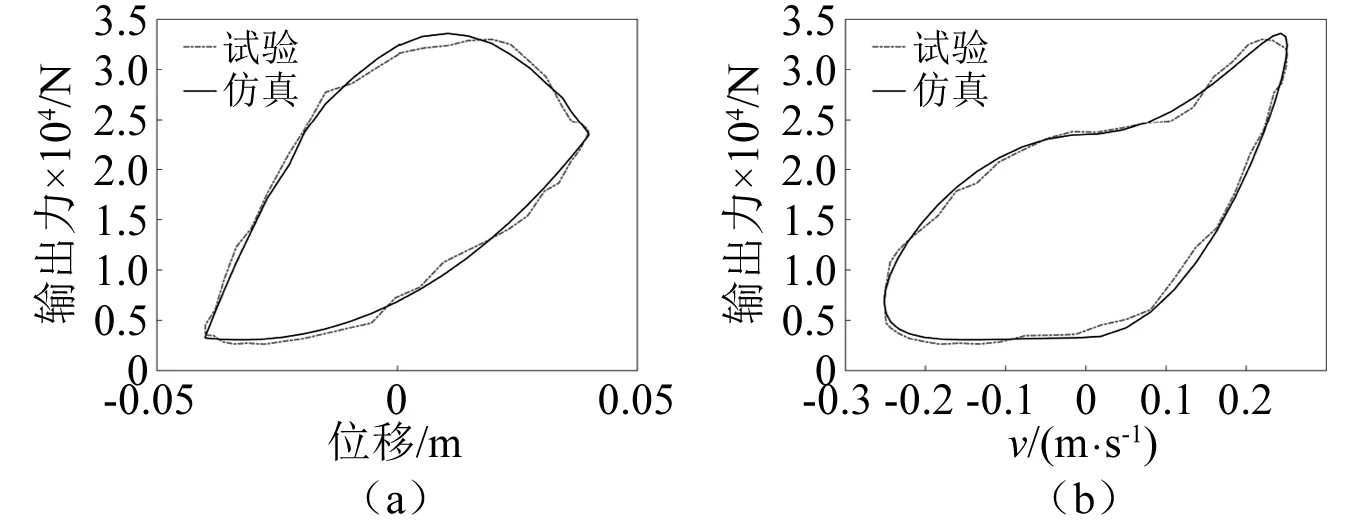
图9 输出力模式4试验与仿真对比图Fig.9 Comparison diagram of output force mode 4 test and simulation

图10 输出力模式8试验与仿真对比图Fig.10 Comparison diagram of output force mode 8 test and simulation

从图8～图10可以看出，仿真结果与试验结果基本一致，证明了本文所建立的油气悬架模型的准确性。然而在曲线的某些地方存在一定的差异，产生这些差异的主要原因主要是台架的安装台与辅助安装吊耳之间存在间隙，导致试验中弹簧输出力的测量误差较大。

为了更加详细的试验数据进行分析，本文将油气悬架的试验示功图面积与仿真示功图面积进行对比，以仿真示功图面积为标准，如表3所示。

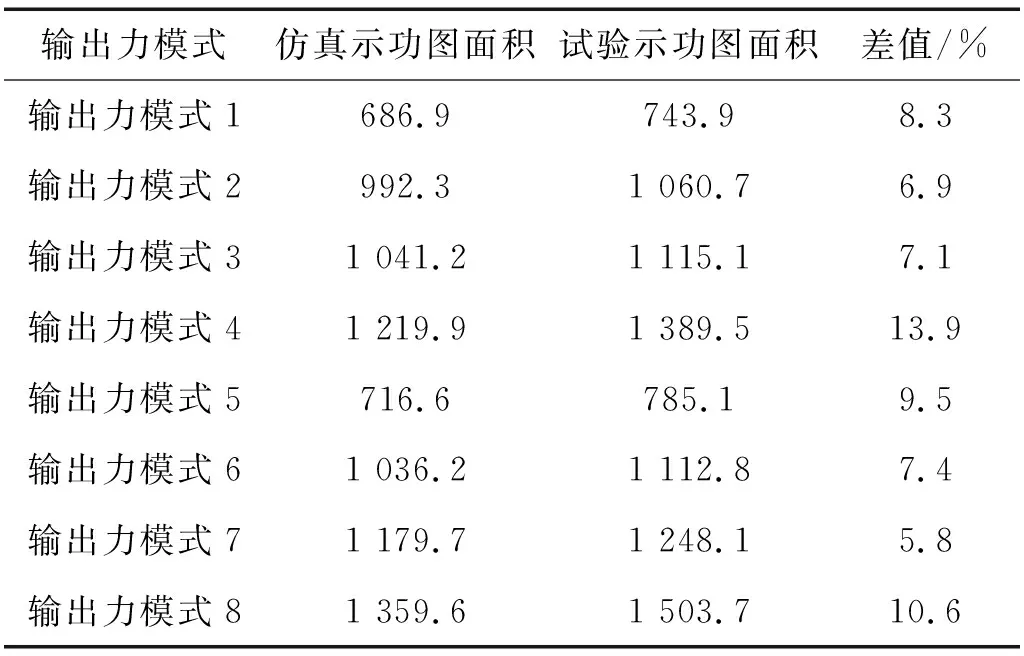
表3 油气悬架输出力示功图面积对比

根据表3的数据分析可知，试验示功图的面积略大于仿真示功图的面积，这是由于在建模过程中忽略了一些影响因素。由于试验数据与仿真数据的误差在合理的范围内，证明了本文所建立的油气悬架系统数学模型的准确性。

3 油气悬架系统刚度阻尼模式匹配

3.1 车辆悬架振动模型

为了方便研究，本文采用应用广泛的只考虑车辆垂向振动的二自由度1/4悬架振动模型作为研究对象，如图11所示。该模型忽略了车身侧倾和俯仰振动，结构简单、便于求解[16]。

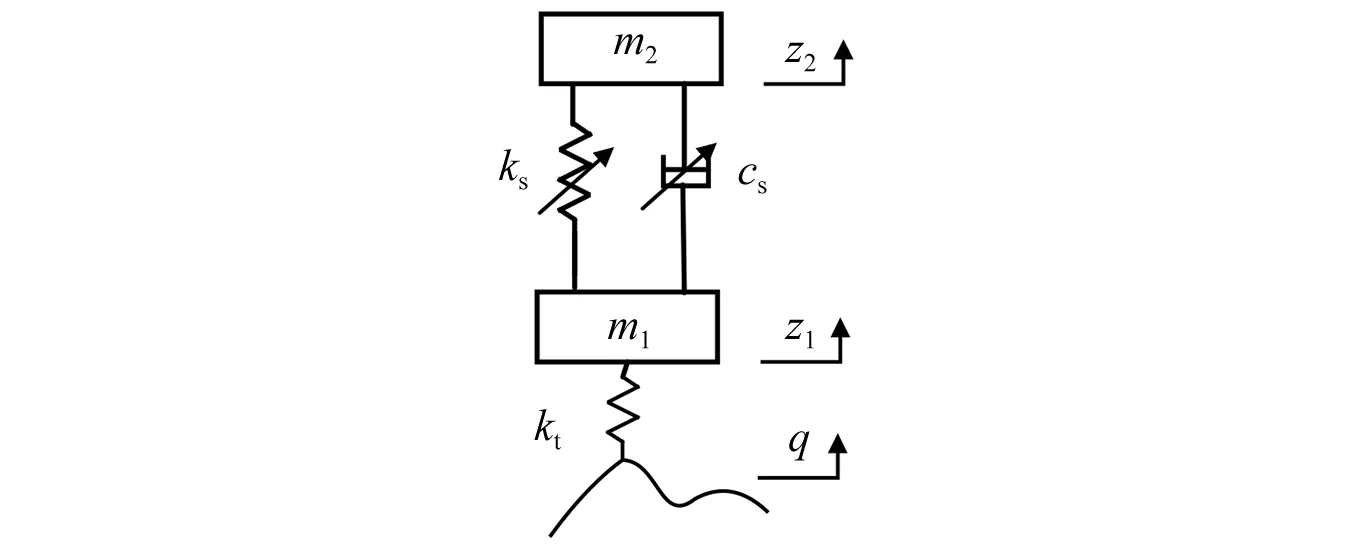
图11 二自由度悬架模型Fig.11 Two degree of freedom suspension model

根据牛顿第二定律，建立系统振动微分方程如下

(24)

式中：m2为簧载质量；m1为簧下质量m1=169 kg；cs为可变阻尼；ks为可变刚度；kt为轮胎刚度kt=584 kN/m；q为路面位移输入；z2为簧载质量的垂向位移；z1为簧下质量的垂向位移。

通过拉普拉斯变换，将时域信号转换为复频域表示可得系统响应量的均方根值如下

(25)

3.2 油气悬架刚度和阻尼参数匹配

为改善油气悬架在复杂工况下的振动特性，提高车辆的行驶性能，本节利用粒子群优化算法，分析不同的路面工况与行驶速度对油气悬架刚度阻尼的影响，并寻找最优的刚度阻尼匹配组合。

粒子的位置与速度更新公式如下所示[17]

(26)

式中：vid为第i粒粒子在第d维的速度；pid为粒子i所经历过的最好位置；pgd为粒子群所经历过的最好位置；xid为粒子i的当前位置。

优化过程中，将油气悬架系统刚度ks与阻尼cs设置为优化变量，将目标函数设置为振动加速度、悬架动挠度与车轮动载荷的综合评价指标F，并设计其约束条件，则参数寻优的数学模型如下

(27)

式中：l1，l2，l3为加权系数，分别为0.6，0.2，0.2；σFd为车轮动载荷均方根值；σfd为悬架动挠度均方根值；ξ为阻尼比；[fd]为限位行程。

c1，c2为学习因子，代表粒子自身学习能力，在0～4取值。标准粒子群算法(particle swarm optimization，PSO)的权重是一个常数，代表PSO粒子对当前速度的承袭度，较大的权重系数能提高算法的全局搜索能力，较小的权重系数会增强算法的局部寻优能力。通过恰当的调整能使粒子既具有很强的全局寻优能力，又具有一定的局部寻优能力。种群数量可根据实际问题的复杂程度自行确定。

为确定最佳的学习因子c1，c2与惯性权重w，以C级路面、车速为50 km/h工况为例，计算不同学习因子与权重对簧载质量振动加速度的改善程度如表4所示。

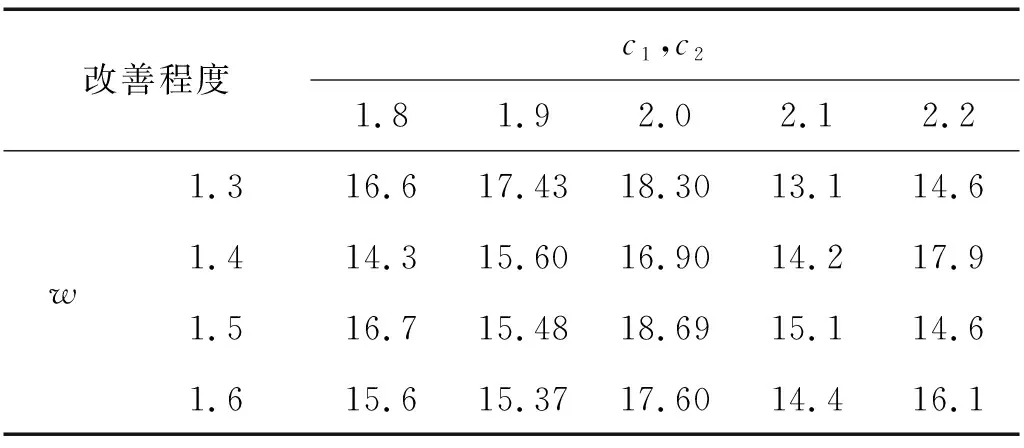
表4 c1，c2与w对簧载质量振动加速度的影响

由表4可知，当c1=c2=2且w=1.5时，对簧载质量振动加速度的优化结果最好。故优化时取c1=c2=2，惯性权重为1.5，种群数量为50，优化结果如表5所示。

表5 不同工况下刚度和阻尼的优化匹配值

从表5可以看出，在同一车速下，刚度阻尼随着路面等级的增大而增大；在同一路面下，阻尼随着车速的增大而增大，在B级、C级路面，车速对优化的刚度值的影响不明显，但在D级、E级路面有明显影响。

将优化前后的参数代入式(25)，对比表5中每种行驶路面下优化前、后簧载质量加速度、车轮动载荷以及悬架动挠度的均方根值，计算结果如表6所示。

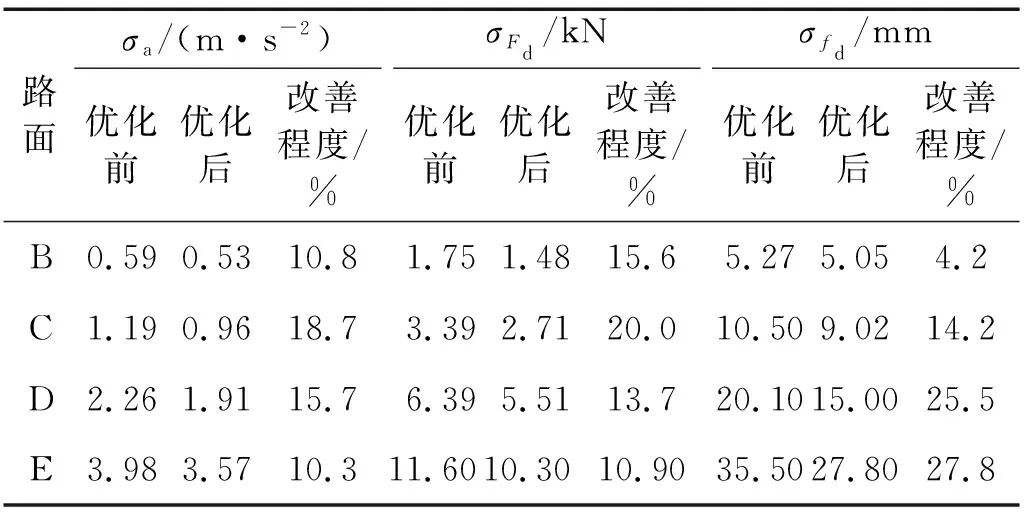
表6 优化前后性能对比

3.3 油气悬架刚度和阻尼模式匹配

从计算得到的刚度阻尼数学模型可以看出其非线性特性，为划分不同的刚度阻尼模式，有必要对其进行线性化处理。将静平衡位置时油气悬架的刚度替代其非线性刚度，将压缩和拉伸行程的平均阻尼力替代整个工作行程的阻尼力。

对式(4)、式(6)取x=0可得线性化刚度

(28)

代入相关参数可得软刚度为124 kN/m，硬刚度为194 kN/m。

油气弹簧压缩行程和复原行程阻尼系数不同，而使压缩行程和复原行程阻尼力不同的原因主要在于阻尼阀系的阻尼系数C1不同，因此需要分别来计算压缩行程与复原行程的阻尼系数。

不同阻尼模式下压缩行程的CY1计算如下

(29)

不同阻尼模式下伸张行程的CL1计算如下

(30)

可得到不同阻尼模式下平均阻尼系数如下

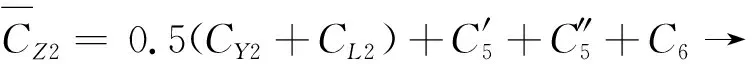
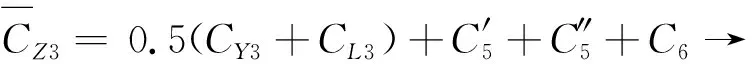
(31)

根据上述值可以将表4中刚度和阻尼的优化匹配值分为5种模式：软刚度小阻尼(M1)，软刚度较小阻尼(M2)，软刚度较大阻尼(M3)，硬刚度较大阻尼(M4)，硬刚度大阻尼(M5)。同时可以得到不同工况下刚度和阻尼模式的匹配方案如图12所示。

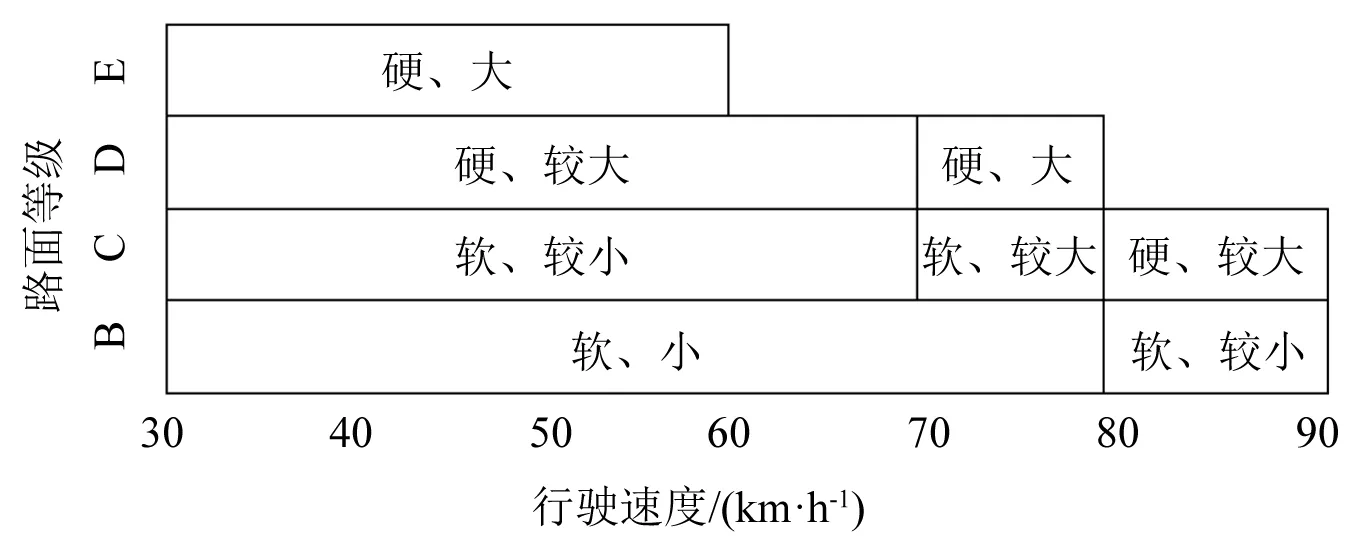
图12 油气悬架刚度与阻尼的匹配策略Fig.12 Matching strategy of stiffness and damping of hydro pneumatic suspension

4 刚度阻尼多模式切换控制研究

油气悬架刚度阻尼多模式自适应切换控制的思路是：根据粒子群优化算法得到不同工况下油气悬架最佳的刚度与阻尼匹配，并存入控制器，车辆行驶时，ECU会采集由传感器测得的车辆行驶状态以及车辆振动响应信息，通过分析当前的行驶工况计算出油气悬架刚度与阻尼的最优模式方案，通过控制开关电磁阀的状态实现对油气悬架刚度阻尼的控制。

路面信息是判定油气悬架刚度阻尼工作模式的一项重要依据。目前有相关参考文献将悬架振动响应作为路面判断的依据，通过计算悬架动行程均方根值来识别路面等级[18]。本文在此研究基础上，通过计算簧载质量振动加速度、悬架动挠度与车轮动载荷的均方根值来判别路面工况。首先确定车辆振动响应均方根值在各级路面的阀值(在各路面等级车速最大工况下的车辆振动响应均方根值)，然后通过设定以下条件进行路面工况判定。

条件1：0≤σa<0.7且0≤σFd<2.07且0≤σfd<3.2

条件2：0.7≤σa<1.5且2.07≤σFd<4.15且3.2≤σfd<6.45

条件3：1.5≤σa<2.8且4.15≤σFd<7.60且6.45≤σfd<12.1

条件4：2.8≤σa<4.7且7.6≤σFd<13.3且12.1≤σfd<20.4

根据路面条件和车速信息设计油气悬架的刚度和阻尼多模式切换的具体规则如表7所示。

刚度阻尼多模式切换油气悬架的数学模型以及二自由度车辆振动模型已在3.1节给出，设计混合随机路面工况，基于Simulink/Stateflow进行模式切换控制系统仿真，将原车与施加模式切换控制后的车身振动加速度、车轮动载荷与悬架动挠度进行对比。

设计混合路面激励：D级路面0～4 s车速65 km/h，4～8 s车速75 km/h；C级路面，8～12 s车速65 km/h，12～16 s车速75 km/h，16～20 s车速85 km/h的混合路面，仿真得到开关电磁阀的状态如图13所示。其与在此混合路面激励下的理论开关电磁阀状态一致，证明了本文对路面工况判别的有效性。

表7 切换控制规则

图13 开关电磁阀状态Fig.13 On-off solenoid status

仿真得到混合路面工况下车身振动加速度、车轮动载荷与悬架动挠度如图14～图16所示。

图14 车身振动加速度Fig.14 Body vibration acceleration

图16 悬架动挠度Fig.16 Dynamic deflection of suspension

从图14～图16可以看出，相对于被动油气悬架，模式切换控制下的油气悬架系统能够有效降低车身振动加速度、车轮动载荷与悬架动挠度的峰值。对仿真结果进行处理分析，得到其均方根值的变化结果如表8所示。

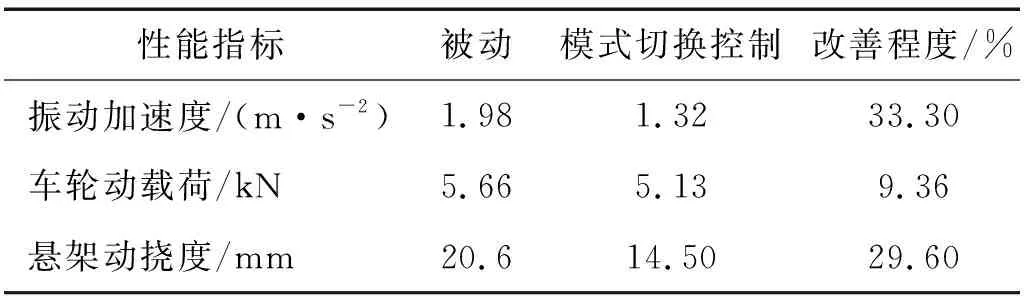
表8 控制前后性能对比

从表8可知，所设计的刚度阻尼多级可调式油气悬架模式切换控制方法能有效改善其振动加速度、悬架动挠度以及车轮动载荷的性能，并且能够很好地与所设计的刚度阻尼多级可调式油气悬架相匹配。

5 结 论

刚度阻尼可调式油气悬架系统在车辆振动控制方面具有广阔的应用前景。本文提出了一种刚度阻尼多级可调式油气悬架系统，通过控制4个开关电磁阀的通断状态，实现了两种刚度模式和4种阻尼模式的调节，利用粒子群优化算法得到油气悬架在不同行驶工况下最优的刚度阻尼匹配值，并设计刚度阻尼多模式切换控制方法，通过仿真研究，主要得出以下结论：

(1)所建立的刚度阻尼多级可调式油气悬架数学模型准确，能够实现两种刚度模式和4种阻尼力模式。

(2)根据粒子群优化算法计算得到的不同行驶工况下刚度阻尼匹配值，能够使得油气悬架系统在不同工况下处于最优状态。

(3)设计的控制策略能够实现油气悬架刚度和阻尼模式的自动切换，从而适应不同的路面工况，并且能够有效地改善油气悬架系统隔振性能。